基于LMD多尺度熵和概率神經(jīng)網(wǎng)絡的滾動軸承故障診斷方法

孟　宗　胡　猛　谷偉明　趙東方

1.燕山大學河北省測試計量技術及儀器重點實驗室，秦皇島，0660042.國家冷軋板帶裝備及工藝工程技術研究中心，秦皇島，066004

基于LMD多尺度熵和概率神經(jīng)網(wǎng)絡的滾動軸承故障診斷方法

孟宗1,2胡猛1谷偉明1趙東方1

1.燕山大學河北省測試計量技術及儀器重點實驗室，秦皇島，0660042.國家冷軋板帶裝備及工藝工程技術研究中心，秦皇島，066004

摘要：研究了一種基于LMD多尺度熵和概率神經(jīng)網(wǎng)絡的滾動軸承故障診斷方法。該方法將故障信號自適應地分解為若干乘積函數(shù)分量，然后將各分量的多尺度熵作為故障特征向量輸入概率神經(jīng)網(wǎng)絡進行模式識別，實現(xiàn)了對損傷位置和損傷程度的診斷。將該方法與基于LMD時域統(tǒng)計量和神經(jīng)網(wǎng)絡的滾動軸承故障診斷方法進行了對比。實驗結果表明，基于LMD多尺度熵和概率神經(jīng)網(wǎng)絡的方法能對滾動軸承故障進行有效的識別與診斷。

關鍵詞：局部均值分解；故障特征提取；多尺度熵；概率神經(jīng)網(wǎng)絡；故障診斷

0引言

滾動軸承是旋轉機械中應用最廣泛的機械部件，也是最容易出現(xiàn)故障的機械部件，其運行狀態(tài)正常與否將直接影響到整個機組的性能，因此對滾動軸承的故障診斷方法和監(jiān)測技術的研究具有重要意義[1]。滾動軸承振動信號包含豐富的故障特征信息，當滾動軸承發(fā)生故障時，振動信號呈現(xiàn)出非線性非平穩(wěn)特性。局部均值分解(localmeandecomposition，LMD) 是一種自適應時頻分析方法，可以將復雜的非平穩(wěn)信號分解為若干個乘積函數(shù)(productfunction,PF)分量之和。每一個PF分量都是由一個純調(diào)頻信號和一個包絡信號相乘得到的，將所有PF分量的瞬時幅值和瞬時頻率組合即可得到原始信號完整的時頻分布[2]。目前，LMD方法在機械故障診斷領域得到廣泛應用[3-7]。

時域統(tǒng)計量(峭度、偏度、能量等)能反映振動信號的分布特性，因此根據(jù)時域統(tǒng)計量指標可以實現(xiàn)故障的判斷[8-9]。程軍圣等[10]提出了一種基于LMD時域統(tǒng)計量和神經(jīng)網(wǎng)絡的滾動軸承故障診斷方法，將時域統(tǒng)計量作為神經(jīng)網(wǎng)絡的輸入特征量來進行故障診斷。時域統(tǒng)計量作為故障特征參數(shù)時，容易受到噪聲等因素的影響，從而影響故障診斷的準確率。

熵是表征系統(tǒng)規(guī)則度及復雜度的物理量，近年來被應用于機械故障診斷領域，多尺度熵(multi-scaleentropy，MSE)能衡量時間序列的復雜性，是時間序列在維數(shù)變化時產(chǎn)生新模式概率大小的量度，具有很強的抗噪聲和抗干擾能力，是量化非線性時間序列復雜度的良好工具[11-15]。神經(jīng)網(wǎng)絡作為一種智能化的數(shù)據(jù)處理方法，具有很強的處理非線性關系數(shù)據(jù)的能力，其中，概率神經(jīng)網(wǎng)絡(probabilisticneuralnetwork，PNN)能夠以任意精度逼近任何連續(xù)非線性函數(shù)，同時具有自組織、自學習和并行處理能力[16-17]。基于此，本文將局部均值分解、多尺度熵和概率神經(jīng)網(wǎng)絡相結合，提出了一種基于LMD多尺度熵和概率神經(jīng)網(wǎng)絡的滾動軸承故障診斷方法，并將該方法與基于LMD時域統(tǒng)計量和神經(jīng)網(wǎng)絡的滾動軸承故障診斷方法進行了對比。實驗結果證明，該方法是有效可行的。

1故障診斷方法

LMD將振動信號分解為一系列的PF分量PF1,PF2,…,PFn和一個殘余量R，每個PF分量由一個包絡信號(PF分量的瞬時幅值)和一個純調(diào)頻信號相乘得到，PF分量的瞬時頻率則由純調(diào)頻信號直接求出。將所有PF分量的瞬時幅值和瞬時頻率組合便可以得到原始信號完整的時頻分布，其分解過程詳見文獻[2]。

多尺度熵基于樣本熵，其計算方法如下：

(1)設一離散原始時間序列為{x1，x2，…，xN}，對原始時間序列進行粗粒化變換，得到新的時間序列：

(1)

j=1，2，…，N/τ

其中，N為離散時間序列長度；τ為尺度因子。原始序列被分割成τ段且每段長為N/τ的粗粒序列。τ=1時，新的時間序列就是原始序列。

(2)給定模式維數(shù)m和相似容限r(nóng)(r>0)，構造時間序列的m維向量：

Xm(i)=(xi，xi+1，…，xi+m-1)

(2)

i=1，2，…，N-m

(3)計算向量Xm(i)與Xm(j)之間的距離：

dij=d(Xm(i),Xm(j))=

max|Xm(i+k)-Xm(j+k)|

(3)

k=0，1，…，m-1；i，j=1，2，…，N-m+1且i≠j

(4)對每個i，計算Xm(i)與Xm(j)的距離，統(tǒng)計其距離小于r的數(shù)目，記為L，將此數(shù)目與距離總數(shù)N-m+1的比值記作Cmi(r)，即

(4)

(5)將Cmi(r)的平均值記作

(5)

(6)把維數(shù)加1，變成m+1，重復步驟(1)～步驟(5)，計算Φm+1(r)。

當N為有限值時，按上述步驟得出的是序列長度為N時的樣本熵估計值：

(6)

重復上述過程，得到不同尺度下的樣本熵值，即為多尺度熵。

概率神經(jīng)網(wǎng)絡是一種前饋型神經(jīng)網(wǎng)絡，包括輸入層、模式層、求和層和競爭層，其結構如圖1所示。輸入層將輸入樣本傳給模式層的各節(jié)點。模式層與輸入層之間通過連接權wij相連，進行加權求和，并通過非線性算子g(zj)：

g(zj)=exp((zj-1)/δ2)

(7)

運算后，傳遞給求和層。該層各個模式單元的輸出為

(8)

其中，X為輸入樣本向量，Wi為輸入層到模式層的連接權值；δ為平滑系數(shù)，它對分類起著關鍵性的作用。求和層則簡單地將由對應樣本中同一類的模式層傳來的輸出(屬于某類的概率)進行累加，即

(9)

式中，m為訓練樣本向量個數(shù)。

圖1　概率神經(jīng)網(wǎng)絡結構

競爭層(輸出層)接收從求和層輸出的各類概率密度函數(shù)，概率密度函數(shù)最大的那個神經(jīng)元輸出為1，其所對應的類即為樣本模式識別結果，其余神經(jīng)元輸出為0。

2基于LMD和神經(jīng)網(wǎng)絡的故障診斷

基于LMD多尺度熵和概率神經(jīng)網(wǎng)絡的故障診斷流程如圖2所示，實驗中，分別選擇故障直徑為0.1778 mm、0.3556 mm、0.5334 mm的滾動體故障信號、內(nèi)圈故障信號和外圈故障信號以及1個正常信號，并定義直徑為0.1778 mm的軸承故障為輕度損傷，直徑為0.3556 mm的軸承故障為中度損傷、直徑為0.5334 mm的軸承故障為重度損傷。因此，滾動軸承的工作狀態(tài)共有10種，將這10種工作狀態(tài)用序號1～10表示，如表1所示。

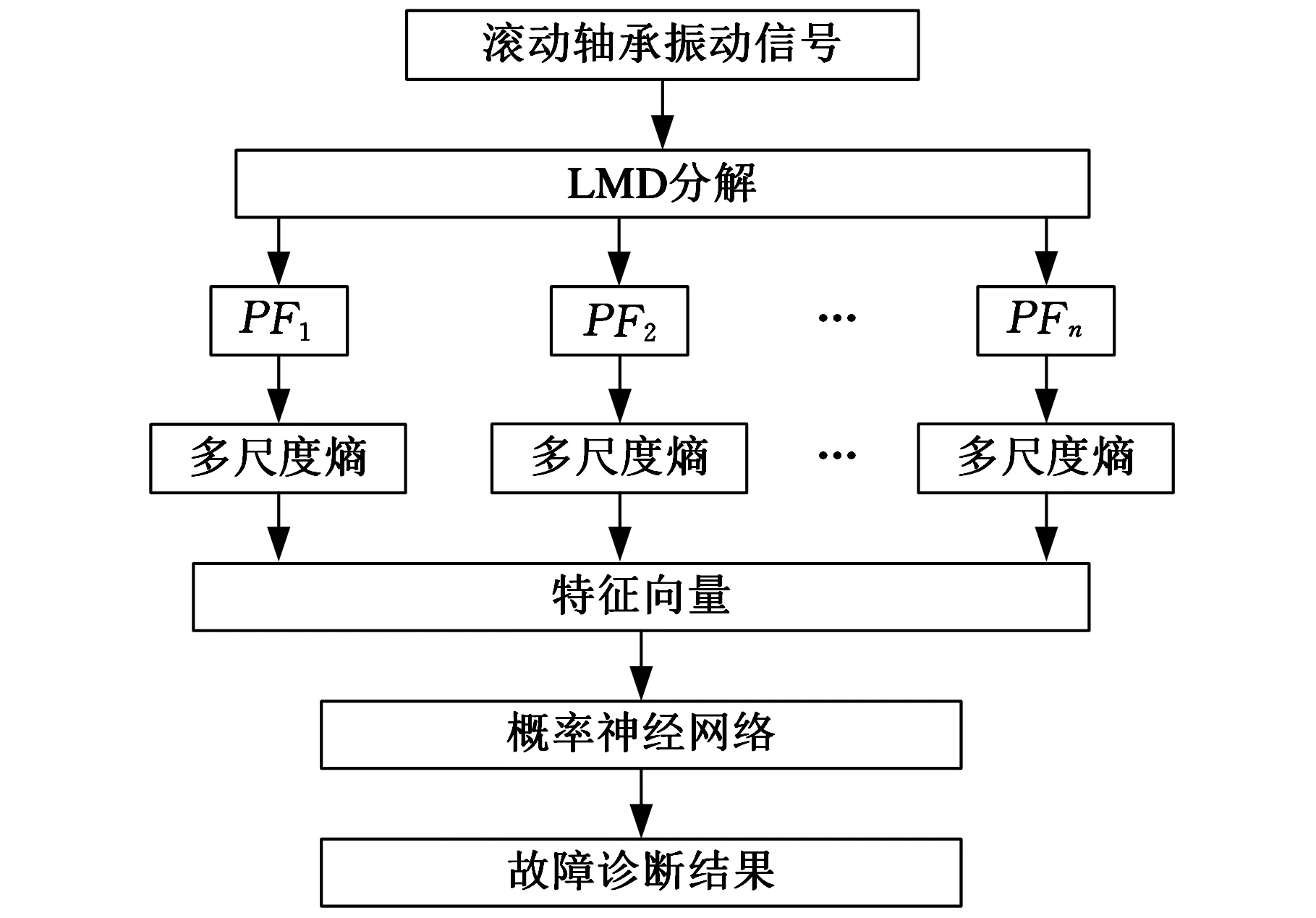
圖2　故障診斷流程圖

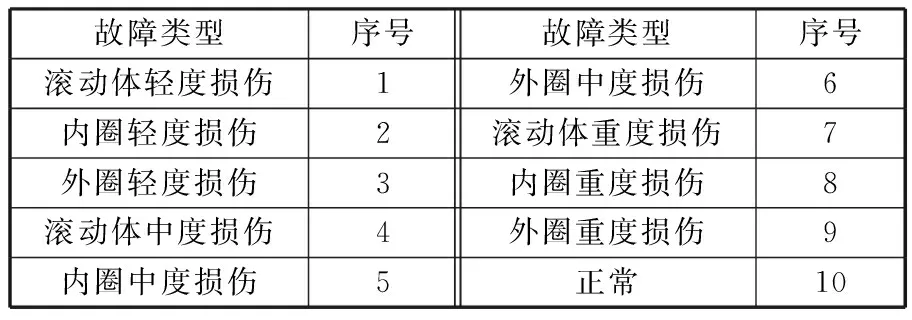
故障類型序號故障類型序號滾動體輕度損傷1外圈中度損傷6內(nèi)圈輕度損傷2滾動體重度損傷7外圈輕度損傷3內(nèi)圈重度損傷8滾動體中度損傷4外圈重度損傷9內(nèi)圈中度損傷5正常10

基于LMD多尺度熵和概率神經(jīng)網(wǎng)絡的滾動軸承故障診斷方法具體步驟如下：

(1)對滾動軸承10種狀態(tài)分別進行10次采樣，將得到的100個振動信號作為樣本。

(2)對每一種狀態(tài)下的原始振動信號進行LMD分解，得到各個PF分量。

(3)選擇前n個PF分量作為研究對象，計算前n個PF分量的多尺度熵。

(4)構造特征向量

T=(PF1(a1)，PF1(a2)，…，PF1(am)，

PF2(a1)，PF2(a2)，…，PF2(am)，…，

PFn(a1) ，PFn(a2)，…，PFn(am))

(5)將構造的特征向量作為概率神經(jīng)網(wǎng)絡的輸入向量，對網(wǎng)絡進行訓練。

(6)將待測樣本輸入到訓練后的概率神經(jīng)網(wǎng)絡，以神經(jīng)網(wǎng)絡的輸出確定軸承的工作狀態(tài)。

3實驗研究

實驗數(shù)據(jù)為美國西儲大學電氣工程實驗室的滾動軸承實驗數(shù)據(jù)。采樣頻率為12 kHz，采樣點數(shù)為5000。對不同狀態(tài)的振動信號進行LMD分解，其中，故障直徑為0.1778 mm(輕度損傷)內(nèi)圈故障信號的LMD分解結果如圖3所示。

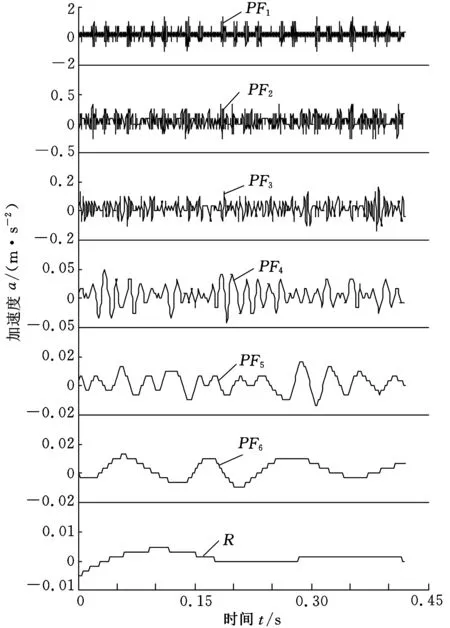
圖3　內(nèi)圈輕度損傷故障信號的LMD分解

由于主要故障信息集中分布在前幾個PF分量，為了避免多尺度熵特征向量的樣本數(shù)據(jù)冗長，本文選取前3個PF分量進行實驗分析。分別對滾動軸承的10種狀態(tài)進行采樣，每種狀態(tài)選取10組數(shù)據(jù)作為樣本進行LMD分解，將分解后前3個PF分量的多尺度熵(尺度因子分別選取5、10、15)作為特征向量，輸入到概率神經(jīng)網(wǎng)絡進行訓練。內(nèi)圈輕度損傷和滾動體中度損傷故障的多尺度熵如表2、表3所示(注：PF1(5)中的5為尺度因子)。

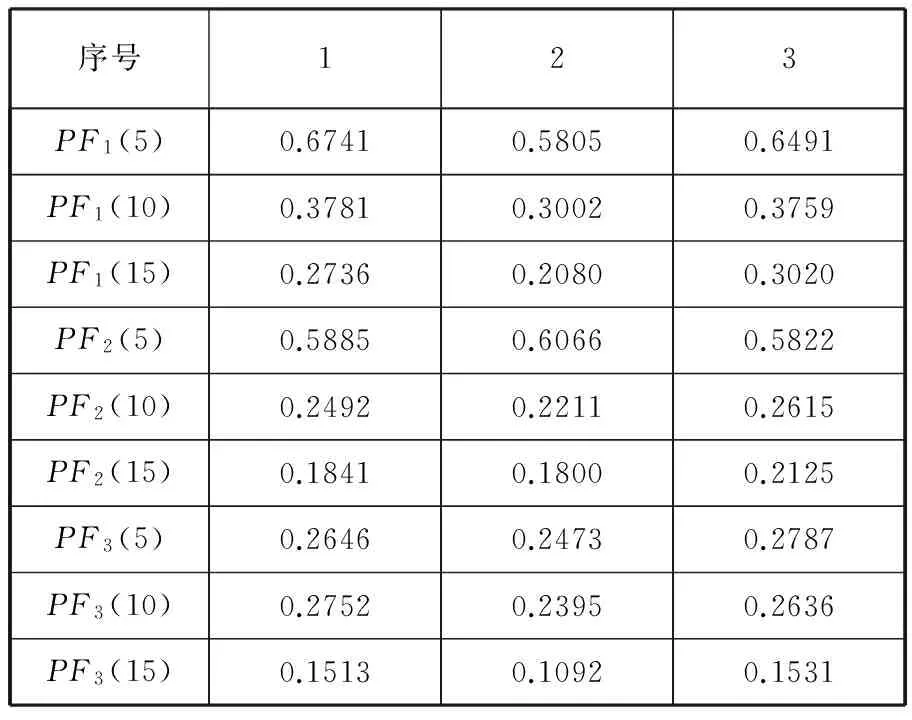
表2　內(nèi)圈輕度損傷故障的多尺度熵

從表2、表3可以看出，滾動軸承在相同工作狀態(tài)下，各PF分量同一尺度因子的熵值比較接近。不同工作狀態(tài)下，各PF分量在同一尺度因子下的熵值相差較大。

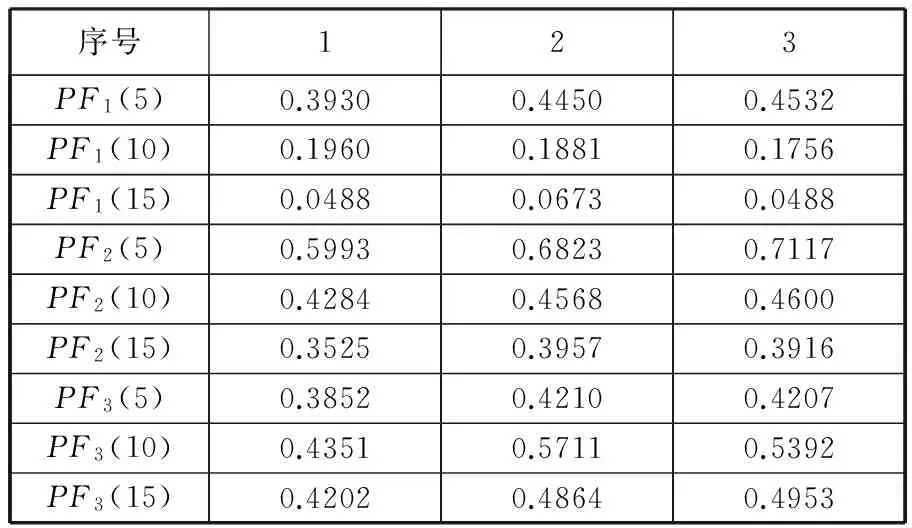
表3　滾動體中度損傷故障的多尺度熵

作為對比，選取前3個PF分量，利用時域統(tǒng)計量峭度Q、偏度P和能量比N作為神經(jīng)網(wǎng)絡的輸入特征量，其中，滾動體中度損傷故障的時域統(tǒng)計量如表4所示。從表4可以看出，同一分量下的同種時域統(tǒng)計量的數(shù)值存在較大波動，不利于滾動軸承的故障診斷。因此，本文利用多尺度熵值作為故障診斷的依據(jù)。將多尺度熵作為神經(jīng)網(wǎng)絡的輸入特征向量進行模式識別。

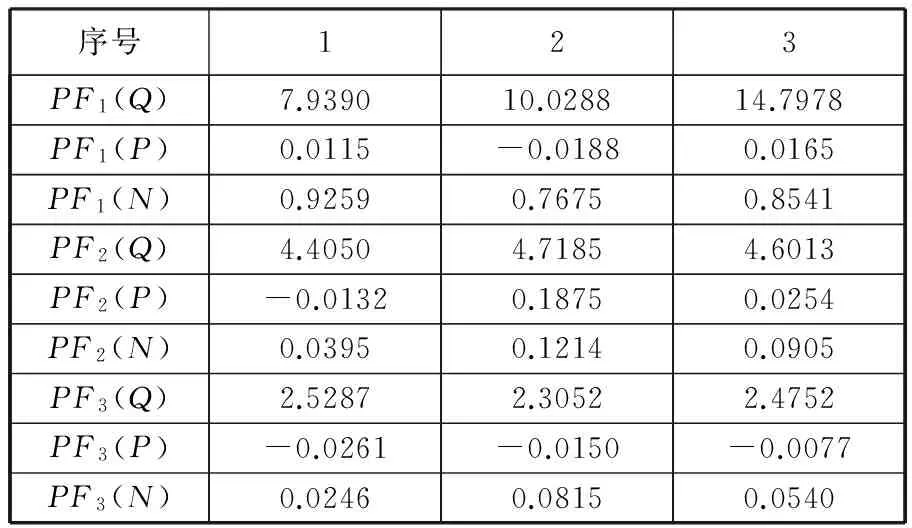
表4　滾動體中度損傷故障的時域統(tǒng)計量

注：PF1(Q)中，Q為時域統(tǒng)計量峭度。

再次對滾動軸承的10種狀態(tài)進行采樣，每種狀態(tài)采樣10次，共得到100組數(shù)據(jù)(作為待測樣本)，將待測樣本進行LMD分解后，計算出各分量的多尺度熵和時域統(tǒng)計量，分別將各分量的多尺度熵和時域統(tǒng)計量作為輸入向量輸入到概率神經(jīng)網(wǎng)絡進行滾動軸承工作狀態(tài)的識別。表5所示為10組待測樣本的診斷結果。

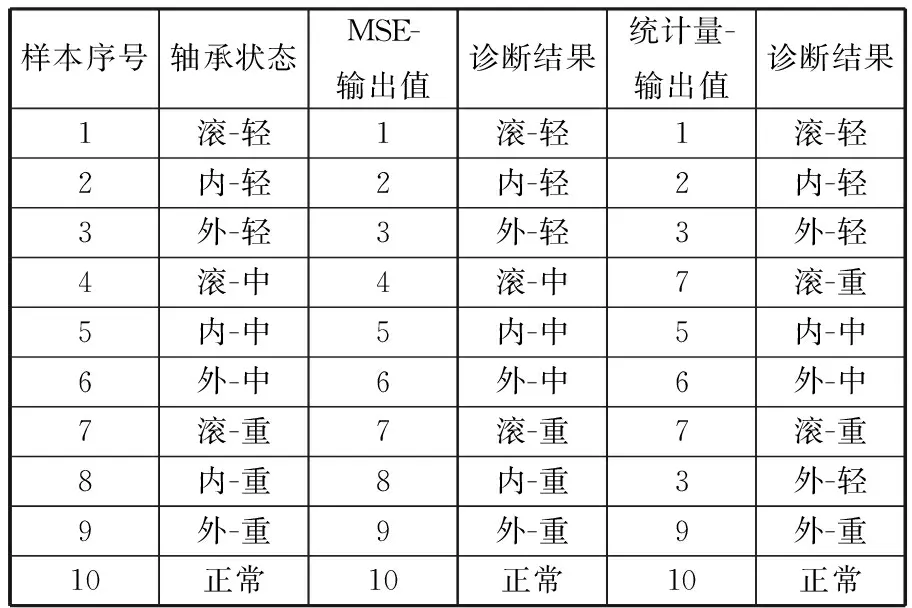
表5　診斷結果

注：表中軸承狀態(tài)“滾-輕”代表滾動體輕度損傷,其他類似。

從表4中可以看出，測試樣本中，基于多尺度熵方法的診斷結果與真實工作狀態(tài)一致，基于時域統(tǒng)計量方法出現(xiàn)2處錯誤診斷。 進一步將基于多尺度熵和基于時域統(tǒng)計量方法的識別率進行對比。對滾動軸承10種狀態(tài)各進行40次采樣，每種狀態(tài)選取10組(共100組)數(shù)據(jù)作為訓練樣本，將每種狀態(tài)剩下的30組(共300組)數(shù)據(jù)作為待檢測樣本進行測試，各診斷方法的識別率如表6所示。

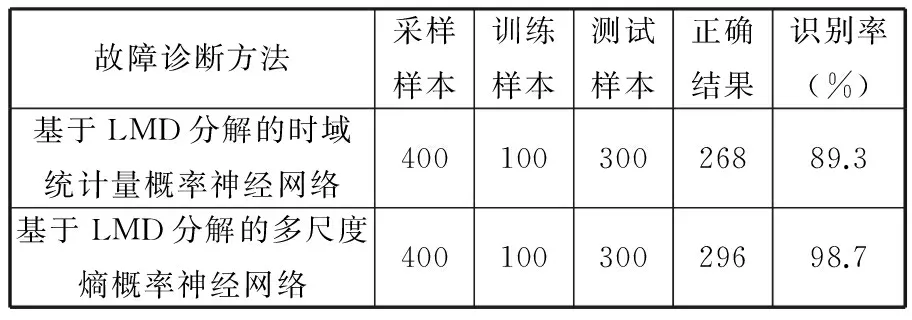
表6　不同診斷方法識別率

從表6中可以看出，基于LMD分解的時域統(tǒng)計量概率神經(jīng)網(wǎng)絡診斷方法的識別率為89.3%，基于LMD分解的多尺度熵概率神經(jīng)網(wǎng)絡診斷方法的識別率為98.7%。與將時域統(tǒng)計量作為模式識別的特征向量相比，將多尺度熵作為模式識別的特征向量具有較高的診斷識別率。實驗結果表明，LMD多尺度熵和PNN結合的滾動軸承故障診斷方法是可行的。因此本文研究的將LMD分解、多尺度熵、概率神經(jīng)網(wǎng)絡相結合的方法能夠有效地進行滾動軸承故障診斷。

4結語

本文提出了一種基于LMD多尺度熵和概率神經(jīng)網(wǎng)絡的故障診斷方法。通過局域均值分解對滾動軸承故障振動信號進行分解，得到了若干PF分量。將多尺度熵作為表征故障特征的參量，求取前三個PF分量的多尺度熵并將其作為概率神經(jīng)網(wǎng)絡的輸入向量，進行滾動軸承工作狀態(tài)的模式識別。實驗結果表明：該方法能夠有效識別出滾動軸承中不同位置、不同損傷程度的故障，提高了診斷精度和識別的能力。

參考文獻：

[1]Zheng Jinde, Cheng Junsheng, Yang Yu.A Rolling Bearing Fault Diagnosis Method Based on Multi-scale Fuzzy Entropy and Variable Predictive Model-based Class Discrimination[J]. Mechanism and Machine Theory，2014，78：187-200.

[2]Smith J S. The Local Mean Decompositionand Its Application to EEG Perception Data[J]. Journal of the Royal Society Interface. 2005，2(5)：443-454.

[3]鐘先友，曾良才，趙春華. 局域均值分解和1.5維譜在機械故障診斷中的應用[J]. 中國機械工程，2013，24(4)： 452-457.Zhong Xianyou，Zeng Liangcai，Zhao Chunhua. Application of Local Mean Decomposition and 1.5 Dimension Spectrum in Machinery Fault Diagnosis[J]. China Mechanical Engineering，2013，24(4)：452-457.[4]張亢，程軍圣，楊宇. 基于局部均值分解的階次跟蹤分析及其在齒輪故障診斷中的應用[J]. 中國機械工程，2011，22(14)：1732-1736.Zhang Kang，Cheng Junsheng，Yang Yu. Order Tracing Analysis Based on Local Mean Decomposition and Its Application to Gear Fault Diagnosis[J]. China Mechanical Engineering，2011，22(14)：1732-1736.[5]王建國，吳林峰，秦緒華. 基于自相關分析和LMD的滾動軸承振動信號故障特征提取[J]. 中國機械工程，2014，25(2)：186-191.Wang Jianguo，Wu Linfeng，Qin Xuhua. Rolling Bearing Vibration Signal Fault Feature Extraction Based on Autocorrelation Analysis and LMD[J]. China Mechanical Engineering，2014，25(2)：186-191.[6]Cheng Junsheng，Yang Yi，Yang Yu. A Rotating Machinery Fault Diagnosis Method Based on Local Mean Decomposition[J]. Digital Signal Processing，2012，22：356- 366.

[7]孟宗，閆曉麗，王亞超. 基于LMD和HMM的旋轉機械故障診斷[J].中國機械工程，2014，25 (21)：2942-2946.

Meng Zong，Yan Xiaoli，Wang Yachao. Rotating Machinery Fault Diagnosis Based on Local Mean Decomposition and Hidden Markov Model[J]. China Mechanical Engineering，2014，25(21)：2942-2946.

[8]程軍圣，楊怡，張亢，等. 基于局部均值分解的循環(huán)頻率和能量譜在齒輪故障診斷中的應用[J]. 振動工程學報，2011，24(1)：78-83.

Cheng Junsheng，Yang Yi，Zhang Kang，et al. Application of Cycle Frequency and Energy Spectrum Based on Local Mean Decomposition to Gear Fault Diagnosis[J]. Journal of Vibration Engineering，2011，24(1)：78-83.

[9]王洪明，郝旺身，韓捷，等. 全失LMD能量熵在齒輪故障特征提取中的應用[J]. 中國機械工程，2015，26(16)：2160- 2164.

Wang Hongming，Hao Wangshen，Han Jie，et al. Full Vector LMD Energy Entropy in Gear Fault Feature Extraction[J]. China Mechanical Engineering，2015，26(16)：2160-2164.

[10]程軍圣，史美麗，楊宇. 基于LMD與神經(jīng)網(wǎng)絡的滾動軸承故障診斷方法[J]. 振動與沖擊，2010，29(8)：141-144.

Cheng Junsheng，Shi Meili，Yang Yu. Roller Bearing Fault Diagnosis Method Based on LMD and Neural Network[J]. Journal of Vibration and Shock，2010，29(8)：141-144.

[11]Costa M，Goldberger A L，Peng C K. Multiscale Entropy Analysis of Biological Signals[J]. Phys. Rev. E，2005，71：021906.

[12]孟宗，王亞超，王曉燕. 基于DLMD樣本熵和模糊聚類的滾動軸承故障診斷[J]. 中國機械工程，2014，25(19)：2634- 2641.

Meng Zong，Wang Yachao，Wang Xiaoyan. Fault Diagnosis of Rolling Bearing Based on DLMD Sample Entropy and Fuzzy Clustering[J]. China Mechanical Engineering，2014，25(19)：2634-2641.

[13]Zhang Long，Xiong Guoliang，Liu Hesheng. Bearing Fault Diagnosis Using Multi-scale Entropy and Adaptive Neuro-fuzzy Inference[J]. Expert Systems with Applications，2010，37：6077-6085.

[14]Liu Huanhuan，Han Minghong. A Fault Diagnosis Method Based on Local Mean Decomposition and Multi-scale Entropy for Roller Bearings[J]. Mechanism and Machine Theory，2014，75：67-78.

[15]鄭近德，程軍圣，楊宇. 基于多尺度熵的滾動軸承故障診斷方法[J]. 湖南大學學報，2012，39(5)：38-41.

Zheng Jinde，Cheng Junsheng，Yang Yu. A Rolling Bearing Fault Diagnosis Approach Based on Multiscale Entropy[J]. Journal of Hunan University，2012，39(5)：38-41.

[16]Chen Xianyue，Zhou Jianzhong，Xiao Han. Fault Diagnosis Based on Comprehensive Geometric Characteristic and Probability Neural Network[J]. Applied Mathematics and Computation,2014，230：542-554.

[17]Wang Changqing,Zhou Jianzhong，Qing Hui. Fault Diagnosis Based on Pulse Coupled Neural Network and Probability Neural Network[J]. Expert Systems with Applications，2011，38：14307-14313.

(編輯張洋)

RollingBearingFaultDiagnosisMethodBasedonLMDMulti-scaleEntropyandProbabilisticNeuralNetwork

MengZong1,2HuMeng1GuWeiming1ZhaoDongfang1

1.KeyLaboratoryofMeasurementTechnologyandInstrumentationofHebeiProvince，YanshanUniversity，Qinhuangdao，Hebei，0660042.NationalEngineeringResearchCenterforEquipmentandTechnologyofColdRollingStrip，Qinhuangdao，Hebei，066004

Abstract:A rolling bearing fault diagnosis method was studied based on LMD multi-scale entropy and probabilistic neural network. In this method, the fault signal was decomposed into several product functions adaptively, and then the multi-scale entropies of each component were feed into the probabilistic neural network as fault feature vectors for pattern recognition to realize the diagnosis of damage position and damage degree. Comparing with the method based on LMD time-domain statistics and probabilistic neural network, the experimental results show that the method based on LMD multi-scale entropy and neural network can identify and diagnose the rolling bearing fault accurately and efficiently.

Key words:local mean decomposition(LMD); fault feature extraction; multi-scale entropy; probabilistic neural network; fault diagnosis

收稿日期：2015-04-02

基金項目：國家自然科學基金資助項目(51575472)；河北省自然科學基金資助項目 (E2015203356)；河北省高等學校科學研究計劃資助重點項目(ZD2015049)；河北省留學人員科技活動擇優(yōu)資助項目(C2015005020)

中圖分類號：TN911.7；TP206.3

DOI：10.3969/j.issn.1004-132X.2016.04.002

作者簡介：孟宗，男，1977年生。燕山大學電氣工程學院教授。主要研究方向為機械設備監(jiān)測與故障診斷、振動信號分析與處理等。發(fā)表論文20余篇。胡猛，男，1990年生。燕山大學電氣工程學院碩士研究生。谷偉明，男，1990年生。燕山大學電氣工程學院碩士研究生。趙東方，男，1989年生。燕山大學電氣工程學院碩士研究生。