一類極點級數的判斷

喻敏，王文波，馬建清，胡佳

?

一類極點級數的判斷

喻敏1，2，王文波1，馬建清1，胡佳1

摘要：探討了一類比較特殊的極點級數的判斷，并從理論上給出證明.

關鍵詞：孤立奇點；極點；零點

YU Min1，2，WANG Wen-bo1，MA Jian-qing1，HU Jia1
（1. School of Science，2. School of Information Science and Engineering，Wuhan University of Science and Technology，Wuhan 430081，China）

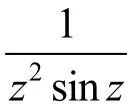
1　極點和零點的定義

定義1［1］145若函數f（z）在z0的洛朗展開式中，負冪項只有有限項，且負冪項的最次冪為m，則稱z0為f（z）的m級極點.

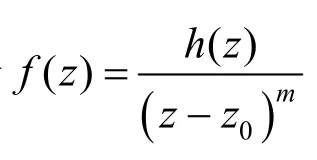
引理［1］152若z0為函數f（z）的m級零點，則f（z）=（z-z0）mφ（z），其中：φ（z）在z0解析，且φ（z0）≠ 0.

在函數f（z）不容易展成f（z）=（z-z）mφ（z）的式子時，用下述充要條件判斷很方便，即z為f（z）的m

0

0級零點的充要條件：fn（z0）=0（n=0，1，…，m-1），fm（z0）≠0.

2　極點的實例及其判定定理

分析 0是f（z）的極點，但是和定義2的形式有點出入.0是分母的零點，由m級零點的充要條件可知，0是sin z的一級零點，則是z2sin z的三級零點.由定義2或者由“f（z）取倒數，零點和極點可以相互轉化”的結論可知，0是f（z）的三級極點.

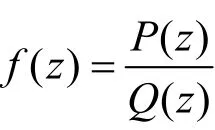
證明 由零點的定義，P（z）=（z-z）mφ（z），Q（z）=（z-z）nφ（z），其中：φ（z），φ（z）在z解析，且

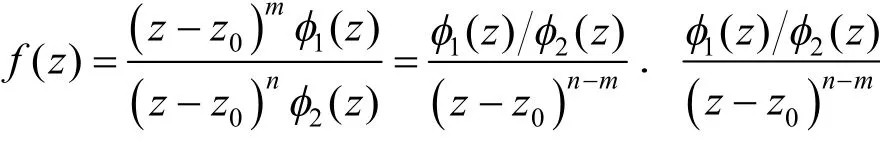
注1 定理只討論了m＜n的情況，類似地，對于m≥ n的情況，容易得出z0為f（z）的可去奇點.

例2 求的孤立奇點，若是極點判斷其級數.

分析 很容易判斷出0是f（z）的極點，但是極點的級數容易判斷為六或者五級，實際上級數應該是三級.用洛朗展式或定理求解此題.

解法2 f（z）是分式，0既是分母的零點，也是分子的零點，很顯然0是分母的六級零點，由判斷零點的充要條件可知，0是分子的三級零點，故由定理可知，0是f（z）的三級極點.

注2 例2既可以用展式求解，也可以用定理求解.洛朗展式和泰勒展式一般都是用間接法展開，即用一些熟知的基本泰勒展式展開.因為洛朗展式不僅在級數里很重要，在判斷極點和留數處也很重要，且由展式判斷極點和求留數時直觀不容易出錯，故推薦使用解法1.

當然，解法2在孤立奇點無法展開為洛朗級數且奇點是分子和分母的零點時起到了至關重要的作用.

分析 此題很容易判斷0是極點，但是其級數很容易誤判為3，而且也容易忽略掉奇點2kπi（k≠0）.

解 0和2k πi是分母的零點，且由零點判斷的充要條件可知，2kπi（k≠0）是函數分母的一級零點，而其中的2πi是分子的一級零點，其分子和分母的零點級數相等，由注1可知，2πi是函數的可去奇點；而其他的奇點0和2kπi（k≠0，1）只是分母的零點，不是分子的零點，故由引理可知，0是函數的四級極點；2kπi（k≠0，1）是函數的一級極點.

參考文獻：

［1］ 西安交通大學高等數學教研室.復變函數［M］.北京：高等教育出版社，1996：145-152

［2］ 王文琦.確定復雜復變函數極點階數的一種方法［J］.山西大同大學學報，2012，28（1）：19-20

［3］ 李茂材，李汝烯，拓行.淺析以復變函數零點性質確定極點階數的方法［J］.貴州教育學院學報，2009，20（6）：7-8

［4］ 霍鳳茹.確定函數的極點（有限數）的級的方法［J］.唐山師范學院學報，2002，24（5）：17-18

［5］ 夏志.一類復變函數極點階數的確定［J］.渤海大學學報，2005，26（1）：49-51

［6］ 馬鳳麗，楊素娟.極點級數的判定方法［J］.高師理科學刊，2012，32（3）：23-25

Judgement about the order of a class of pole

（武漢科技大學 1. 理學院，2. 信息科學與工程學院，湖北 武漢430081）

Key words：isolated singularity；pole；zero point

Abstract：Gives residue judgement about the order of a special class of pole and proves it theoretically.

中圖分類號：O172.2

文獻標識碼：A

doi：10.3969/j.issn.1007-9831.2016.05.006

文章編號：1007-9831（2016）05-0018-03

收稿日期：2016-01-10

基金項目：武漢科技大學教學研究項目（2014X68）；冶金工業過程系統科學湖北省重點實驗室開放基金項目（Y201506）

作者簡介：喻敏（1975-），女，湖北武漢人，講師，碩士，從事小波分形研究.E-mail：yufeng3378@163.com