基于JSS矩陣的裝配精度分配方法

呂　程　劉子建

湖南大學汽車車身先進設計制造國家重點實驗室，長沙，410082

?

基于JSS矩陣的裝配精度分配方法

呂程劉子建

湖南大學汽車車身先進設計制造國家重點實驗室，長沙，410082

摘要：采用小位移旋量描述結合面誤差，分析了典型結合面的誤差傳遞屬性。定義了結合面的信息集成表達符號，結合多色集合理論，建立了描述裝配關系、結合面類型、結合面誤差傳遞屬性的結合面符號矩陣，進而提出了裝配誤差傳遞路徑的搜索方法。分析了結合面間的關系對誤差傳遞的影響，建立了結合面的實際誤差傳遞屬性矩陣，獲取了各誤差分量的傳遞路徑,明確了影響裝配體精度的關鍵誤差分布。根據多體運動學原理建立了裝配體誤差模型，結合裝配體精度要求進行了結合面精度分配，進而實現了結合面相應幾何要素的精度分配。為正向公差設計與裝配過程精度控制提供了依據。最后通過實例分析，驗證了該方法的可行性與實用性。

關鍵詞：小位移旋量法；多色集合理論；JSS矩陣；誤差傳遞路徑；精度分配

0引言

在機械產品的生命周期中，精度設計與控制是決定產品最終質量的關鍵因素之一[1]。傳統的精度設計主要依賴于經驗，不能直接滿足產品精度要求，難以獲得較低的制造成本[2]。高精度復雜機械產品的精度設計體現出了高難度及重要性，是目前精度理論研究的重點之一。

國內外學者對精度設計方法展開了大量的研究，并獲得了相應的成果。楊波等[3]研究了生長型設計中尺寸鏈以及形位公差項目的自動生成，建立了公差進化設計的基本過程模型。金秋等[4]從資金的時間價值角度改進公差成本模型，建立了并行公差設計的目標函數，實現了公差優化設計。Kumar等[5]使用拉格朗日乘子法在最低成本基礎上同時分配設計公差與制造公差。Jeang[6]采用蒙特卡羅法進行模擬實驗，采用響應面法進行數據分析，獲得了最優的公差設計方案。文獻[7-8]提出了基于新一代GPS體系框架的公差的數學建模技術及公差設計理論和方法。上述方法為公差設計與優化提供了途徑，但對于結構復雜的機械產品，依然缺少一般意義上直接高效的產品精度設計指導方法。因此，本文從描述復雜裝配體的裝配關系入手，搜索裝配體的誤差傳遞累積路徑，并結合精度要求，進行裝配結合面以及零件幾何要素的精度分配，旨在為公差設計以及加工精度與裝配精度的控制提供明確的依據。

1裝配關系描述

結合面是由不同零件上的表面依據裝配關系，通過裝配連接形成的一對配合面。零件誤差在結合面不斷累積傳遞，使結合面成為連接零件、傳遞誤差的關鍵節點。相互關聯的結合面形成了復雜的裝配誤差傳遞路徑，成為影響產品精度的重要因素。

1.1結合面的誤差傳遞屬性

本文采用小位移旋量法(small displacement torsor, SDT)[9]描述結合面的誤差變動，即S=(R,D)=(α,β,δ,u,v,w)，R=(Rx,Ry,Rz)=(α,β,δ)，D=(Dx,Dy,Dz)=(u,v,w)，其中，α、β、δ分別為繞x、y、z軸轉動的微小變動,u、v、w分別為沿x、y、z軸平動的微小變動。

根據幾何形狀與配合類型可將結合面劃分為平面固定結合面、平面非固定結合面、圓柱面間隙配合結合面以及圓柱面過盈配合結合面。其中，平面固定結合面指形成結合面的兩平面為固定連接關系，裝配完成后兩平面間不能相對運動，而平面非固定結合面指裝配完成后形成結合面的兩平面間可以進行相對運動。為便于描述復雜的結合面屬性，本文定義了典型結合面的符號，具體如圖1所示。

結合面的誤差傳遞屬性指結合面受自身幾何與配合特征影響，對所要傳遞的不同性質的誤差分量進行選擇性傳遞的特性，可用S描述。根據GPS標準中的恒定度概念，當直線、平面等幾何要素繞(或沿)某坐標軸轉動(或平動)時，若幾何要素的形態特征保持不變，則稱其具有該方向上的恒定度，對應的SDT分量為0[10]。假設平面結合面法向以及圓柱結合面軸向均與坐標軸N(N為x或y或z)平行,則各類結合面的轉動誤差傳遞屬性R=(Rx,Ry,Rz)與平動誤差傳遞屬性D=(Dx,Dy,Dz)見表1。

表1中圓柱間隙配合誤差分量的不確定性與裝配體拓撲結構有關，后文將進行詳細闡述。

1.2裝配關系多色集合矩陣

多色集合理論可用相同數學模型模擬不同問題對象，已被廣泛應用于各種信息建模領域[11-12]。本文采用結合面符號取代現有多色集合矩陣中的布爾型元素值。根據裝配體中結合面的組成，建立能綜合描述裝配關系、結合面類型以及結合面誤差傳遞屬性的結合面符號(joint surface symbols，JSS)矩陣。JSS矩陣是一種新型的多維裝配信息集成描述方法，它拓寬了裝配關系的信息表達維度，具有更強的仿真能力，且便于計算機實現。

根據圖2所示裝配體的裝配關系，可用JSS矩陣描述其裝配關系，如圖3所示。圖2中，P1至P6為零件，F1至F10為結合面。

由表1可知，結合面誤差傳遞屬性與局部坐標系的方向直接相關。為保證各結合面誤差傳遞屬性描述的一致性，在建立JSS矩陣前需統一各結合面局部坐標系的方向。

2基于JSS矩陣的誤差傳遞路徑搜索

復雜裝配體的精度分析需要從裝配整體的角度明確零件誤差是如何傳遞累積進而影響裝配體精度的。因此，需要先明確復雜裝配體的誤差傳遞路徑。

為方便計算，采用一組二進制數LPi表示裝配體中與零件Pi關聯的所有結合面，LPi中的各元素與JSS矩陣中的零件元素行值對應，如P1關聯的結合面為LP1=(1111100110)。通過邏輯“積”運算，可得任意兩零件間可傳遞誤差的結合面：

Exji=LPj∧LPi

(1)

其中，i≠j，Exji中值為1的數對應的結合面編號即為兩零件間可傳遞誤差的結合面編號。

基于JSS矩陣搜索誤差傳遞路徑的步驟如下：

(1) 根據精度分析需求，確定誤差分析的基準件與精度輸出件。以基準件為起點，搜索所有與之可進行誤差傳遞的零件，即根據式(1)算出Exji不全為0的零件。將這些零件作為基準件在誤差傳遞方向上的下一級零件，并從JSS矩陣中去掉當前基準件元素。

(2) 分別以步驟(1)中的各下一級零件(精度輸出件除外)為基準件，重復步驟(1)的搜索方法，直至當前基準件已無下一級零件，搜索結束。誤差傳遞路徑的搜索過程呈樹狀結構展開。以圖2中P1為基準件，P2為精度輸出件，搜索過程如圖4所示。圖4中，箭頭表示誤差傳遞方向，(F3/F4)表示P1和P2間有F3和F4兩結合面。因F1、F2不在P1到P2間的路徑上，與所求問題無關，因此后文不再討論。從基準件到精度輸出件的誤差傳遞路徑如下：

Path1：P1→P2

Path2：P1→P3→P2

Path3：P1→P5→P2

Path4：P1→P6→P5→P2

零件作為誤差傳遞路徑的載體，根據零件在誤差傳遞方向上的關系，將誤差傳遞路徑分為串聯路徑和并聯路徑兩種。結合面提供了相鄰零件間誤差傳遞的通路，根據結合面在誤差傳遞方向上的關系，可分為串聯通路和并聯通路，如圖5所示。

采用6位二進制數表示結合面誤差傳遞屬性。各位二進制數代表的誤差分量與S中的各分量相對應。串并聯路徑(或通路)的誤差傳遞屬性Ssc、Spc可分別通過邏輯“積”與邏輯“和”求解：

(2)

式中，n、m分別為串并聯的結合面數量。

(3) 并聯的誤差傳遞路徑與結合面通路為誤差的傳遞提供了多個途徑，因此，須考慮誤差分量的性質、結合面間的相互位姿等影響因素，才能確定各結合面的實際誤差傳遞屬性，進而確定各路徑的實際誤差傳遞屬性。在此，通過引入裝配定位優先等級的概念消除誤差分量傳遞路徑的不確定性。裝配定位優先等級是指在裝配過程中，根據功能要求，通過工藝手段使各結合面定位精度得到保證的先后順序。一般地，定位優先等級越高獲得的裝配精度也越高，對應的結合面即成為某些誤差分量傳遞的主導因素。基于此，并聯結合面通路實際誤差傳遞屬性的計算方法如下：

(3)

其中，從1到m是按照從裝配定位優先等級從高到低的順序依次排列的并聯結合面。Sm0為根據表1確定的結合面m的誤差傳遞屬性，Sm為m的實際誤差傳遞屬性。

受并聯關系影響的結合面類型及其實際誤差傳遞屬性分析如下：

(1) 平面固定結合面。設平面法向N=z，實際裝配中，誤差分量δ、u、v常受其他零件或結構而非結合面本身形狀與結構特征的限制。因此，當結合面上述誤差分量可通過其他路徑或通路優先確定時，結合面的實際誤差傳遞屬性為(110001)，否則誤差傳遞屬性不變，δ、u、v具體誤差值由裝配定位系統決定。

(2) 圓柱面間隙配合結合面。由于圓柱面間隙配合結合面存在徑向間隙，使被裝配零件的徑向位姿具有不確定性。設表1中不確定的誤差分量為Run、Dun，若結合面本身裝配定位優先等級較高，則由間隙引起的Run、Dun上的位姿誤差可視為零件的幾何位姿誤差，Run≠0、Dun≠0。否則Run=0、Dun=0。圓柱面間隙配合結合面的實際誤差傳遞屬性為

(4)

式中，Sci(Fj)為將Fj視為過盈配合時的誤差傳遞屬性；SPai為裝配定位優先等級高于Fj的結合面所在并聯誤差傳遞路徑或通路的實際誤差傳遞屬性；n為路徑及通路的數量。

圖3中結合面的實際誤差傳遞屬性如圖6所示。

3零件幾何要素的精度分配

因不同形狀結合面對裝配誤差傳遞的影響不同，對應結合面誤差的衡量方式也不同。平面結合面誤差體現為兩零件理想表面間的相對位姿變動，圓柱結合面誤差體現為孔軸理想軸線間的相對位姿變動。因此，結合面誤差包含了組成結合面的零件表面加工誤差與在裝配過程中引入的定位誤差等裝配過程誤差。因裝配過程誤差可通過裝配工藝加以控制，故在零件精度分配時可假設該誤差為零。按照誤差傳遞方向，形成結合面誤差的兩幾何要素分別為結合面前向幾何要素和后向幾何要素。

由前文確定的具體誤差傳遞路徑可知與裝配精度相關的誤差節點分布。因此，可結合裝配精度要求，根據裝配誤差與結合面誤差間的具體函數關系，進行結合面精度分配。

3.1以結合面為節點的裝配誤差建模

根據齊次坐標變換法[13-14]，結合面誤差變換矩陣可表示為

(5)

其中，i代表結合面，矩陣中各參數為結合面誤差變動的SDT分量。誤差傳遞過程如圖7所示。

根據多體運動學原理[15]，誤差傳遞路徑的誤差變換矩陣為

(6)

其中，E為單位矩陣，Mpa為從基準件到精度輸出件的位姿變換矩陣，M0為零誤差情況下從基準件到精度輸出件的位姿變換矩陣。D0,1為從基準坐標系到第一個結合面前向理想幾何要素的位姿變換矩陣，Dj-1,j為從第j-1個結合面的后向理想幾何要素到第j個結合面的前向理想幾何要素間的位姿變換矩陣，其值與零件基本尺寸相關，為已知。En為精度輸出表面的誤差變換矩陣(為方便表達，可將En視為結合面)。n為路徑中串聯的結合面數量，Ej為第j個串聯結合面的誤差變換矩陣。當Ej處對應的兩零件間存在并聯結合面通路時，式(6)中相應部分的位姿變換矩陣為

Dj-1,jEjDj,j+1=

(7)

式中，r為兩零件間并聯的結合面數量；Eji為當前兩零件間的第i個并聯的結合面誤差變換矩陣。

由于各結合面的誤差分量均為微小值，故在具體計算中可略去Epa中二階及高階項，進而可得總體裝配精度與各結合面誤差分量之間的函數關系[16]。3.2結合面精度分配

由于各路徑的累積誤差均影響精度輸出件的位姿，故各路徑傳向精度輸出件的同種誤差分量值應相等，否則將使輸出件在該誤差分量方向上的位姿無法確定，導致裝配失敗。因此，各并聯路徑傳遞的裝配誤差分量應滿足下式：

EA,k=Epi,k

(8)

i=1,2,…,mk=α,β,δ,u,v,w

式中，m為可傳遞當前誤差分量的并聯路徑總數；Epi,k為路徑i的誤差分量k的值；EA,k為裝配體的誤差分量k的值。

在實際裝配中，零件幾何要素的誤差為定值，而結合面處可能引入裝配過程隨機誤差。由于最短路徑上串聯的結合面最少，可認為裝配誤差僅由零件加工誤差引起。此時，其他并聯路徑可通過零件的選擇和裝配過程誤差的調整來保證各并聯路徑裝配誤差的一致性。因此，可認為裝配體精度由最短路徑的零件精度決定，故將最短路徑作為裝配精度分配的主要對象。

產品根據功能要求確定的裝配精度為結合面及零件的精度分配提供了依據。根據裝配精度要求，以某一誤差分量的精度分配為例，進行結合面誤差分配的流程如圖8所示。

結合面精度分配的具體步驟如下：

(1) 根據裝配精度要求選擇可傳遞對應誤差分量的路徑，建立各路徑的裝配誤差數學模型，獲得精度要求指定的裝配誤差分量表達式，根據精度要求，確定上述表達式的誤差變動不等式：

(9)

式中，Ek,min、Ek,max為裝配精度要求的誤差分量k的極限值；Q為不等式的誤差分量項數；i為相關結合面的序列號,i∈{1,2,…,n}；ei為結合面i的誤差分量，ei∈{α,β,δ,u,v,w}；fq(ei)為ei的一次項。

(2) 選擇步驟(1)中最短路徑的誤差變動不等式。若不等式包含的結合面誤差分量數大于1，則根據各誤差項的誤差分量對裝配體精度與功能的影響程度確定各誤差項的權值，求各誤差分量范圍：

WqEk,min≤fq(ei)≤WqEk,min

(10)

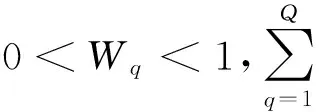
(3) 將求得的誤差分量代入并聯路徑的誤差變動不等式，然后選擇變量最少的不等式，重復步驟(2)，進行結合面精度分配，直至完成所有結合面的精度分配。

3.3零件幾何要素誤差變動范圍的確定

由結合面誤差的構成可知，結合面誤差與零件幾何要素誤差的關系可表示為

Ei=Ef1×Ef2-1

式中，Ef1、Ef2分別為結合面的前向、后向幾何要素分別從各自的理想位姿到實際位姿的變換矩陣。

已知Ei的誤差變動范圍，可獲得兩零件幾何要素的誤差分量變動不等式。零件幾何要素精度分配的過程與結合面精度分配過程類似，在此不再贅述。

根據裝配體精度要求可確定相關零件幾何要素的誤差變動范圍，為零件公差設計、裝配過程中零部件的裝配精度控制提供了重要的依據。

4實例分析

實例目標如下：實現圖9所示泵體的零件相關幾何要素的精度分配；要求零件P4、P5的齒輪在x方向的相對距離誤差u為±0.016 mm。

設P4為基準件，基準坐標系定在P4的齒輪中心，P5為精度輸出件。進行零件精度分配的步驟如下：

(1) 建立裝配體的JSS矩陣。如圖10所示。

(2) 進行誤差傳遞路徑搜索，結果如圖11所示。所有的誤差傳遞路徑如下：

Path1：P4→P1→P2→P3→P5

Path2：P4→P1→P2→P5

Path3：P4→P1→P5

Path4：P4→P3→P2→P1→P5

Path5：P4→P3→P2→P5

Path6：P4→P3→P5

Path7：P4→P2→P1→P5

Path8：P4→P2→P3→P5

Path9：P4→P2→P5

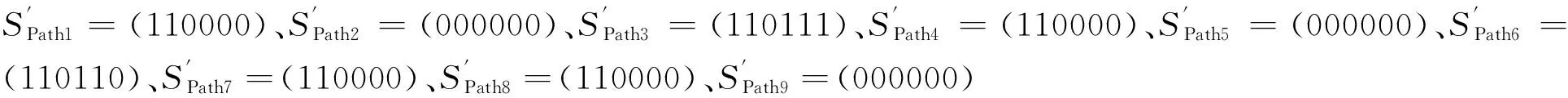
(4) 根據式(5)～式(7)建立裝配誤差模型：

Epa3=E+DP4,F3EF3DF3,F8EF8DF8,P5-DP4,P5

Epa6=E+DP4,F4EF4DF4,F9EF9DF9,P5-DP4,P5

式中，Epa3、Epa6分別為路徑Path3、Path6的誤差變換矩陣；DP4,F3為從零件P4到結合面F3前向理想幾何要素的位姿變換矩陣；EF3為結合面F3的誤差變換矩陣，其他同理。

計算可得裝配誤差分量u的變動不等式為

取各結合面誤差分量項的權值相等，根據式(10)，可求得各結合面誤差分量的變動區間，見表2。

各結合面處零件幾何要素誤差分量項取相等權值，由式(10)可求得對應幾何要素的誤差變動，見表3。表3中，Fi-Pj表示結合面i處，零件j的幾何要素。

5結語

本文在多色集合理論的基礎上，以集成描述結合面信息的符號代替現有裝配關系多色集合矩陣的元素取值空間，建立了JSS矩陣，提升了裝配關系矩陣的仿真能力。針對并聯結合面誤差傳遞屬性間的相互影響，分析了典型并聯結合面的實際誤差傳遞屬性求解方法。完成了基于JSS矩陣的裝配體誤差傳遞路徑搜索，并求得各路徑的實際誤差傳遞屬性。基于多體運動學建立了誤差傳遞路徑的裝配誤差模型。實現了符合裝配體精度要求的結合面精度分配，進一步實現了影響裝配精度的關鍵零件幾何要素的精度分配。研究結果為公差設計、裝配過程中的精度控制與檢測等提供了重要依據。

參考文獻：

[1]孛朝旺, 楊志宏, 王林博,等.尺寸工程技術綜述與展望[J].計算機集成制造系統, 2014,20(3):464-470.

Bo Chaowang, Yang Zhihong, Wang Linbo, et al.Review and Outlook of Dimensional Engineering[J].Computer Integrated Manufacturing Systems, 2014,20(3):464-470.

[2]張巖, 莫蓉.基于灰色粒子群算法的飛機裝配公差多目標優化設計[J].計算機集成制造系統,2014,20(8):1870-1878.

Zhang Yan, Mo Rong.Multi-objective Optimization Design Based on Grey Particle Swarm Optimization Algorithm for Aircraft Assembly Tolerance[J].Computer Integrated Manufacturing Systems, 2014,20(8): 1870-1878.

[3]楊波,高常青,黃克正,等.生長型設計中公差進化設計方法研究[J].機械工程學報, 2012, 48(7): 147-155.

Yang Bo,Gao Changqing,Huang Kezheng,et al.Tolerance Evolutionary Strategy in Incremental Growth Design[J]. Journal of Mechanical Engineering, 2012, 48(7): 147-155.

[4]金秋,莫帥.基于改進成本公差模型的并行公差優化設計[J].天津科技大學學報, 2010, 25(5): 53-56.

Jin Qiu,Mo Shuai.Concurrent Tolerancing Optimization Design Based on improved Cost-tolerance Model[J]. Journal of Tianjin University of Science & Technology, 2010, 25(5): 53-56.

[5]Kumar M S,Stalin B.Optimum Tolerance Synthesis for Complex Assembly with Alternative Process Selection Using Lagrange Multiplier Method[J].The International Journal of Advanced Manufacturing Technology,2009, 44(3/4): 405-411.

[6]Jeang A.Optimal Tolerance Design by Response Surface Methodology[J].International Journal of Production Research, 1999, 37(14): 3275-3288.

[7]彭和平.基于新一代 GPS 框架的公差設計理論與方法研究[D].武漢:華中科技大學, 2009.

[8]徐旭松.基于新一代 GPS 的功能公差設計理論與方法研究[D].杭州：浙江大學, 2008.

[9]吳兆強.基于小位移旋量的公差模擬建模及公差分析[J].機械設計與制造,2010(1): 205-207.

Wu Zhaoqiang. Stimulated Tolerances Modeling Based on Small Displacement Torsors and Tolerances Analysis[J]. Machinery Design & Manufacture,2010(1): 205-207.

[10]張嬌娜.基于GPS標準體系的形狀公差建模及其誤差評價技術[D].杭州：浙江大學, 2007.

[11]Pavlov V V.Polychromatic Graph of Mathematics Simulation for Technical System[C]//the Proceedings of Scientific and Technical Conference (CAD-88).Plovdiv, 1988:8-10.

[12]李宗斌,高新勤,趙麗萍.基于多色集合理論的信息建模與優化技術[M].北京：科學出版社, 2010.

[13]黃強, 李青鋒.機床通用誤差模型的建立及應用[J].中國機械工程,2013,24(12): 1626-1630.

Huang Qiang, Li Qingfeng.Buliding and Application of General Model for Machine Tool Errors[J].China Mechanical Engineering,2013,24(12): 1626-1630.

[14]Rocha C R,Tonetto C P,Dias A.A Comparison between the Denavit-Hartenberg and the Screw-based Methods Used in Kinematic Modeling of Robot Manipulators[J]. Robotics and Computer-Integrated Manufacturing,2011, 27(4):723-728.

[15]Chen J S. Computer-aided Accuracy Enhancement for Multi-axis CNC Machine Tool[J].International Journal of Machine Tools and Manufacturing,1999,35(4): 593-605.

[16]呂程，劉子建.基于裝配定位優先級的并聯結合面誤差建模[J].中國機械工程, 2015,26(24)：3295-3301.

Lü Cheng，Liu Zijian.Parallel Joint Surface Error Modeling Based on Assembly Positioning Priority[J].China Mechanical Engineering, 2015, 26(24)：3295-3301.

(編輯陳勇)

Assembly Accuracy Allocation Method Based on JSS Matrix

Lü ChengLiu Zijian

State Key Laboratory of Advanced Design and Manufacture for Vehicle Body,Hunan University, Changsha，410082

Key words：small displacement torsor(SDT) method；polychromatic sets theory;joint surface symbol(JSS) matrix；error transfer path；accuracy allocation

Abstract：Joint surface error was described by SDT,typical joint surface error transfer properties were analyzed. Information integrated expression symbols of joint surfaces were defined, combined with the polychromatic sets theory,JSS matrix,was established,that could describe assembly relationship,joint surface type and error transfer properties,and then assembly error transfer path search method was proposed,critical error distribution that affected the precision of assembly was identified. Assembly error model was established based on the multi-body kinematics principles,and combined with assembly accuracy requirements,the accuracy allocation of joint surface and the relevant geometric element were implemented, then the basis was provided for tolerance design and accuracy control during assembly process.At last, the feasibility and practicability of the proposed method was verified by example analyses.

收稿日期：2015-04-10

基金項目：國家自然科學基金資助項目( 51175161，51475152)

作者簡介：呂程，女，1988年生。湖南大學汽車車身先進設計制造國家重點實驗室博士研究生。研究方向為機械產品公差設計理論及裝配精度分析與控制。劉子建(通信作者)，男，1953年生。湖南大學汽車車身先進設計制造國家重點實驗室教授、博士研究生導師。

中圖分類號：TH115

DOI：10.3969/j.issn.1004-132X.2016.02.002