圓錐形件拉深成形應力應變的直接積分解法

秦泗吉　鄧　超　楊　莉　孔曉華　王耀華

?

圓錐形件拉深成形應力應變的直接積分解法

秦泗吉鄧超楊莉孔曉華王耀華

燕山大學,秦皇島,066004

摘要：針對圓錐形件的拉深成形，在平面應力和比例加載條件下，采用參數方程的方法分析得到了變形區應變的微分方程。可在圓錐形件的凸緣區、凹模圓角區及錐壁區分別根據應變微分方程，代入相應的邊界條件，采用直接積分得到應力、應變解，將應用于軸對稱平面內的積分解法推廣至分析圓錐形件的拉深成形問題。在凸緣區，錐角等于0；在錐壁區，錐角等于一定值；在凹模圓角區，將圓角部分的弧段分成若干個微錐段，每一微錐段都可分別作為一個小的等錐角的錐環處理。采用該方法，不僅可以計算錐形件的拉深成形問題，而且可以計算曲面形狀已知的一般軸對稱曲面零件的成形問題。用直接積分法替代迭代法求解非線性方程，使求解過程大大簡化。選取厚0.87mm的ST16板材進行了拉深成形實驗，以板坯內層為測量面，測量了凸緣區、凹模圓角區和錐壁區的應變分布，理論計算結果與實驗結果一致。

關鍵詞：板材成形；圓錐形零件拉深；平面應力模型；直接積分解法

0引言

在板材沖壓成形中,圓錐形件是典型的曲面類零件,在成形過程中既有徑(經)向受拉、周向受壓的拉深成形區域，一般又存在雙向拉應力的脹形區域，在凹模圓角和凸模圓角區域還會產生彎曲變形。變形過程中，可能出現的兩種失穩形式是破裂和起皺，其中,起皺失穩可能出現在凸緣區和懸空的錐壁區。圓筒形件可以認為是當圓錐形件的大端尺寸接近小端尺寸時的特例，而其他軸對稱曲面類零件又可以看作由一系列的微錐組成。此外，圓錐形零件在板材沖壓成形中也有廣泛應用，如汽車燈罩、消音器后蓋及輪轂防塵罩、電振動喇叭筒和圓錐滾子軸承保持架等都是圓錐形零件[1]。因此,對圓錐形件成形的研究是有理論意義和實際意義的。

許多學者對包括圓錐形件的軸對稱成形問題進行了研究，涉及拉深[2-4]、脹形[5]和內孔翻邊[6]等問題。在分析軸對稱成形問題時，主要采用兩種假設模型[2]:一是板坯厚度不變的平面應變假設，二是板平面(或曲面)法線方向應力為零的平面應力假設。當假設板坯厚度不變時，可使分析過程大大簡化,所以許多學者常用這種假設模型[2-4,7-9]。

由于板材成形在很多情況下,垂直于板平面或曲面方向上無力的作用或作用力很小(即使采用液壓成形方式,板坯法線方向的應力也很小[10]),此時板材成形過程更接近平面應力狀態,因此,按平面應力模型進行分析更接近實際情況。

關于平面內的軸對稱成形問題，在平面應力和比例加載等假設條件下,李敏華[11]給出了參數方程的直接積分求解方法,改進了Nadai[12]、Millenson等[13]給出的需要不斷迭代才能得到解析解的方法，顯著簡化了求解過程。文獻[8,14]將軸對稱問題的參數方程分析方法用于求解軸對稱成形板平面內沖壓成形問題,給出了不考慮厚度變化時用參數方程形式表示的凸緣區應力顯式表達式。但由于軸對稱成形問題多數情況下都涉及凸緣區以外的成形區域，這些區域的形狀是錐面或曲面，無法采用平面應力假設條件下的直接積分解法。這也是該方法沒有得到推廣應用的原因之一。

本文將求解平面內軸對稱問題的分析方法推廣至求解圓錐形件的成形問題，給出了基于參數方程的積分解法。針對圓錐形零件的拉深成形，將變形區主要劃分為凸緣區、凹模圓角區、懸空錐壁區和凸模圓角區。對前三個區域都給出了基于積分解法的應力、應變解，采用厚0.87mm的ST16板材進行了圓錐形件拉深實驗，測量了應變分布，理論計算值與實驗結果一致。采用本文方法,還可將積分解法推廣至求解一般軸對稱成形問題。

1變形協調方程及平衡方程

1.1變形協調方程

如圖1所示，從圓盤或圓環的平板毛坯變形為圓錐形殼體，變形后某一微錐形環內外半徑分別為r和r+dr,若對應半徑是r的質點變形后的徑向位移為u,則變形前微圓環的內外緣半徑分別為r-u和r-u+dr-du。

α為錐面母線與豎直方向的夾角，又稱為半錐角。由應變的定義，可以得到經向應變ερ和周向應變εθ[11]:

(1)

(2)

消去u,可得

(3)

對于平面內的軸對稱成形，可令α=π/2。

1.2微分平衡方程

在圓錐形件的成形中，每一變形質點的主軸方向為經向、緯向及法向，對應的三個方向的應力分別表示為σρ、σθ和σz。截取一微錐殼環,然后用過軸對稱線的平面將其剖開,得到一半微錐環,其受力情況如圖2所示。

圖2中符號含義如下:OO′為對稱軸線；r、α的含義與圖1相同;σρ、σρ+dσρ分別為上下緯端面上作用的經向應力;σθ為作用于微錐殼體上的緯向應力;t、t+dt分別為上下緯端面處的厚度;ds為微錐殼體的母線長度;p為作用于殼體下表面的單位壓力。

分別在軸線方向和水平方向列平衡方程，有

cosαd(σρtr)=prsinαds

(4)

σθtds-sinαd(σρtr)=prcosαds

(5)

由式(4)、式(5)，并注意到ds=dr/sinα,得

d(σρtr)=σθtdr

(6)

式(6)與軸對稱平面內成形的微分方程在形式上完全相同，也可表示成

(7)

2參數方程及邊界條件

對于圓錐形件成形的錐壁區,忽略板厚方向的應力,根據等效應力的定義,有

(8)

式中,σ為等效應力;R為板厚方向性系數。

參照平面內的軸對稱成形問題的解法[11],應力可以用參數方程的形式表示:

(9)

式中,ω為參數。

比例加載條件下,等效應變ε的參數表達式為

(10)

由應力參數方程式(9)，得

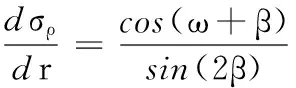
(11)

將式(9)、式(11)代入式(7),并利用體積不變條件dt/t=-dερ-dεθ,得

(12)

設材料的等效應力應變關系滿足σ=Bεn(B為強度系數,n為硬化指數),則

(13)

將式(13)代入式(12),得

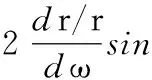
(14)

由參數方程式(10),得

(15)

將式(10)、式(15)代入式(3)，得

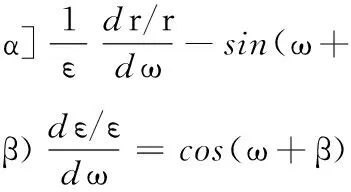
(16)

在微分方程(式(14)和式(16))中,變量ε、r是參變量ω的函數，當邊界條件已知時,方程的解是確定的。

圖3所示為圓錐形件拉深至某一位置時的各變形區,AB為凸緣區,BC為凹模圓角區,CD為錐壁區,DE為凸模圓角區,EF為錐底。

當拉深位置一定時,若采用直母線假設,則DC為直線,錐形件的錐角α已知。設α=α0,α0可由拉深位置、模具幾何尺寸以及板厚變化情況確定。

板材平面內軸對稱問題可認為是圓錐形件成形的一個特例，因式(14)不含變量α,對凸緣區的變形,在求解時令α=π/2,代入式(16)即可。

圓錐形件拉深時,因凹模圓角對板坯的法向作用力很小，凹模圓角區板坯的變形可以近似認為只有經向和緯向應力。如圖3所示，設凹模圓角處的板坯形狀與凹模圓角輪廓形狀一致，在凹模圓角處,BC與AB、CD分別在B、C點相切。將圓弧BC分成若干個弧段，當弧段尺寸較小時，該弧段接近直線段，其對應的變形區可作為一個小錐環處理。設小弧段的長度為ΔS，該處切線與豎直方向夾角為αi，令α=αi，應變微分方程和求解過程與錐壁區相同。

對于圓錐形件的拉深成形問題，采用積分解法的計算次序是凸緣區、凹模圓角區和懸空側壁區。在凸緣變形區,設F為壓邊力,μ為摩擦因數,tw為凸緣外緣對應的板坯厚度,ω0為參數初始值,ε0為應變初始值。則邊界條件如下：當ρ=Rw(Rw為凸緣外緣半徑)時

σρ=F/(Rwtw)

ω0=2π-arccosm-β

ε0=ln(R0/Rw)

當不考慮摩擦時,σe初值為0,ω0=3π/2-β。

在凹模圓角區和懸空側壁區，只要給出初始點的應變作為邊界條件，由式(14)和式(16)，應變與坐標位置的關系是確定的。凸緣區與凹模圓弧交接的位置對應的應變可作為凹模圓角區的初始值,凹模圓角區與懸空側壁區交接位置對應的應變可作為懸空側壁區的初值。

3直接積分解法

將式(14)、式(16)聯立,消去dr/r,設方程為

(17)

b=2cos(ω+β)sinβcosω-cos(ω+β)n/ε

c=2εcos(ω+β)sinβsinω-sin(ω+β)

d=1-exp(2εcosβsinω)/sinα

e=-sin(ω+β)f=εcos(ω+β)

對于給定的邊界條件,一般需要采用迭代解法才能得到微分方程式(17)的解。

對于等錐角的圓錐形件成形問題,已知邊界條件,即當ω=ω0時,ε=ε0,采用直接積分解法求任意ω對應的應變ε的計算過程和收斂性可說明如下:

(1)將區間(ω0,ω)N等分,各值為ωi(i=0,1,…,N),對應的應變值為εi(i=0,1,…,N),每一區間的增量Δω=(ω-ω0)/N。

(2)根據微分學的知識，有

(18)

式中,o(Δω)為比Δω高級的微分項。

因此,當參變量由ω0增加為ω1時,對應的應變ε1可以近似表示為

(19)

(3)一般地,當已知ωi-1(i≥1)對應的應變為εi-1時,其臨近點ωi對應的應變εi近似表示為

(20)

(4)對于任意ω,對應的應變值近似為

(21)

在步驟(2)～(4)中,當ω和ε已知時,由式(17)可得到該點的一階導數。因此,式(21)又可寫為

(22)

根據積分的定義，有

(23)

N值越大,計算精度越高。步驟(1)～(4)的求解過程實際上是用數值方法計算積分問題,即

(24)

在計算過程中,每次求出ε后,代入式(14)或式(16)可求出dr/r,積分后可得到r。這樣就可得到等效應變ε與位置r之間的關系，進而可求出應力、應變。

4圓錐形件拉深成形應力應變分布

4.1圓角區和錐壁區α值的確定

4.1.1凹模圓角區α值的確定

拉深過程中,板坯經過凹模圓角時的變形非常復雜,為了簡單起見,設板坯經過凹模圓角時,板坯內層保持凹模圓角的外輪廓形狀。如圖4所示，根據幾何關系可建立質點位置半徑r和α的關系:

(25)

4.1.2錐壁區α值的確定

分析表明,懸空側壁區錐角對應變分布的影響很大。如圖3所示,設從凸緣區邊緣A至凸模圓角與錐底連接點E為變形區。

在計算出凸緣區、凹模圓角區的應變分布之后,可按體積不變條件確定錐角。實際計算時，暫以變形前后總面積不變，初步確定錐角α0,再根據計算后的厚度變化按體積不變進行修正。計算表明,采用面積不變假設與體積不變假設結果相差不大,一般需修正2～3次就能使體積計算值收斂。

采用積分法求解，實際是將板坯分成若干微段，成形后的體積很容易得到,體積可按下式進行計算:

(26)

式中,Vi為各部分的體積;rai、rbi分別為各計算區間的起止點對應的徑向坐標;ri、ti分別為位置半徑和相應位置的板坯厚度;αi為對應計算段的板坯所在弧或平面與軸對稱線夾角。

4.2應力、應變分布

取凹模內半徑Rd=26.82 mm，凸模外半徑Rp=20 mm，凹模圓角rd=13 mm,凸模圓角rp=5 mm，原始毛坯半徑R0=55 mm,板厚0.87 mm。壓邊力取5 kN，板坯與凹模、板坯與壓邊圈之間的摩擦因數都取0.06,不考慮板坯在凹模圓角處的摩擦。材料選用ST16板材，性能參數經拉伸實驗確定:B=511.4 MPa,n=0.26,R=2.243。拉深相對位置Rw/R0分別為0.919、0.878和0.838，采用上述計算方法得到的應變分布和應力分布分別如圖5～圖10所示。

由前面的理論分析可知，應力值與材料強度系數B成比例關系，為了簡明起見，圖8～圖10采用了應力與強度系數的比值。

圖5～圖7顯示,經向應變為正值,除接近凸模圓角附近的很小區域外，其他區域的緯/周向應變都為負值。從凸緣外緣到凸模圓角，板坯厚度應變由正變為負。隨著拉深過程的進行,變形程度逐漸增大,經向應變、周向應變絕對值最大值也逐漸增大。

圖8～圖10表明,經向應力都為拉應力，周向應力分為拉和壓兩個區域。經向應力最大值隨拉深變形程度的增大而逐漸增大。周向應力在大部分區域都為負值(壓應力)，但在接近凸模圓角的區域為正值(拉應力)，且隨著變形程度的增大，拉應力值也增大。接近凸緣區變形性質為經向受拉、周向受壓的拉深，接近凸模圓角區變形為雙向受拉的脹形，且隨著變形程度的增大，雙向應力越來越接近。

5圓錐形件拉深成形實驗

圓錐形件拉深成形實驗選取ST16板坯,板坯幾何尺寸、性能參數、拉深工藝參數和模具幾何參數與前面理論計算相同。實驗過程中先在圓形毛坯上印制網格，再進行拉深成形實驗，測量成形后板坯的應變分布。

拉深成形時，將板坯印制有網格的面放置到凹模一側，變形后這個表面即為圖4所示的內層，其與模具輪廓形狀最接近。為了減小摩擦的影響，選擇了薄膜潤滑。如圖11所示，三個試件拉深高度H從左至右依次為22.87 mm、27.26 mm和32.53 mm,對應的法蘭外緣相對半徑Rw/R0分別為0.919、0.878和0.838。

成形后的試件用自動應變測量系統VialuxAutoGrid進行測量。為了真實地反映應變的分布情況，將拉深試件的整個凸緣區、凹模圓角區和懸空側壁區所有網格節點都作為測量點,將經向應變、周向應變測量值與相應各點所在位置半徑之間的關系表示在圖12～圖14上。圖中光滑曲線為理論值，離散點為實驗值。實驗得到的經向應變、周向應變應變值都分別集中在一個條帶區域內。

實驗和計算結果表明,采用直接積分法得到的理論計算值與實測的周向應變值一致,經向應變值的理論計算結果與實測值在凹模圓角區、接近凹模圓角的凸緣,以及接近凸模圓角的懸空側壁區相差稍大,但變化趨勢基本一致。由于理論計算采用了薄膜理論的平衡方程式，沒有考慮彎曲的影響，另外采用直母線假設等，這些都可能造成了理論計算與實際存在一定的偏差。板坯在凹模圓角的彎曲變形主要是沿經向的,因而對周向應變影響不大。

6結論

(1)對圓錐形零件的成形問題，給出了基于參數解法的直接積分解法和具體求解過程，這一方法避免了進行復雜的迭代求解。

(2)選取0.87mm厚的ST16板材和一定的模具尺寸及工藝條件,對圓錐形件拉深成形，求解得到了板坯拉深至不同位置時的應力應變分布。

(3)進行了圓錐形件拉深成形實驗，實驗測量了凸緣區、凹模圓角區和懸空側壁區的應變分布。結果表明，在相同變形條件下采用直接積分法計算的周向應變與實測結果較接近，而經向應變在某些區域差別稍大，但趨勢基本一致。

參考文獻:

[1]萬敏.圓錐形零件沖壓成形極限的研究[D].哈爾濱：哈爾濱工業大學, 1995.

[2]FazliA,ArezooB.PredictionofLimitingDrawingRatioConsideringtheEffectiveParametersofDieArcRegion[J].J.Mat.Proc.Technol.,2012,212(4):745-751.

[3]任運來，呂亞臣，彭加耕，等.相對厚度對錐形零件拉深成形的影響[J].機械工程學報，2010, 46(8):51-55.

RenYunlai,LüYachen,PengJiageng,etal.EffectofRelativeThicknessonTaperedPartDrawing[J].JournalofMechanicalEngineering, 2010, 46(8):51-55.

[4]秦泗吉. 軸對稱拉深成形凸緣區應力應變解析求解[J]. 機械工程學報, 2011, 46(24):20-25.

QinSiji.AnalyticalSolutionofStressandStraininFlangeDeformationinAxisymmetricDeepDrawingProcess[J].JournalofMechanicalEngineering, 2011, 46(24):20-25.

[5]戴春俊.板材脹形過程應變分析的實驗-數值混合法[D].哈爾濱：哈爾濱工業大學,2013.

[6]紀蓮清，謝歡.內孔翻邊時變形區應力應變規律研究[J]. 鍛壓技術,2007,32(1):20-24.JiLianqing,XieHuan.StressandStrainRuleStudiesofDeformactionAreaofInsideHoleFlange[J].Forging&StampingTechnology,2007,32(1):20-24.[7]趙軍.圓錐形件拉深成形智能化的研究[D].哈爾濱：哈爾濱工業大學，1997.

[8]梁炳文,胡世光.板料成形塑性理論[M].北京:機械工業出版社,1987.

[9]ThiruvarudchelvanS,TanMJ.ANoteonFluid-pressure-assistedDeepDrawingProcesses[J].J.Mat.Proc.Technol., 2006,172(2):174-181.

[10]WuYS,WangXY,XiaJC.MultipointBlankHolderforceControlinHydroformingofFuelTank[J].ChineseJournalofMechanicalEngineering，2006，19(2)：200-204.

[11]李敏華.硬化材料的軸對稱平面塑性平面應力問題的研究[M].北京:科學出版社,1960.

[12]NadaiA.PlasticBehaviorofMetalsintheStrainHardeningRange,PartI[J].J.Appl.Phys.,1937,8(3):205-213.

[13]MillensonMB,MansonSS.DeterminationofStressesinGas-turbineDisksSubjectedtoPlasticFlowandCreep[R].NewYork:NACA,1948.

[14]劉幺和,胡世光.板料的n、r值對應力應變分布的影響[J].鍛壓技術, 1982,7(3):11-18.

LiuYaohe,HuShiguang.TheeffectofnandronDistributionsofStressandStrain[J].Forging&StampingTechnology,1982,7(3):11-18.

(編輯陳勇)

ADirectIntegralMethodtoSolveStressandStrainofConicalPartsinDeepDrawingProcess

QinSijiDengChaoYangLiKongXiaohuaWangYaohua

YanshanUniversity,Qinhuangdao,Hebei,066004

Keywords：sheetmetalforming;conicalpartindeepdrawing;planestressmodel;directintegralmethod

Abstract:Undertheconditionsofplanestressandproportionalloading,differentialequationsofstrainandstressindeformationzoneofconicalpartindeepdrawingwereobtainedbythemethodofparametricequation.Aftersolvingthedifferentialequationsunderthecorrespondingboundaryconditionsintheregionsofflange,diecornerandconicalwalloftheconicalpartthestressesandstrainsmightbeobtainedrespectivelyineveryregionsbythedirectintegralmethod.Theapplicationsofthedirectintegralmethodwereextendedfromsolvingthein-planeaxisymmeticsheetmetalformingproblemstoanalyzeconicalpartdeepdrawingprocess.Theconicalangleswereequaltozeroandacertainvalueinflangeregionandconicalwallrespectively.Thediearcregionsmightbedividedintoseveralsmallsegmentsandeachofthemcouldbetakenasaconicalpartwithconstantconicalangle.Thismethodwasappliedtosolveconicalpartdeepdrawingproblemsandtoanalyzetheformingproblemofaxisymmetriccurvedpartswithgivenprofileshape.Asthesubstituteofiterationmethod,thedirectintegralmethodwasappliedtosolvenonlinearequationsandthesolvingprocesscouldbesimplifiedgreatly.Theexperimentsofconicalpartdeepdrawingwerecarriedoutbyusing0.87mm-thickST16sheetandthestraindistributionsinflange,diearcandconicalwallregionsweremeasured.Itshowsthattheanalyticalsolutionsbythedirectintegralmethodareaccordantwithexperimentalresults.

收稿日期：2015-04-09

基金項目：國家自然科學基金資助項目(51175451)

作者簡介：秦泗吉,男,1963年生。燕山大學機械工程學院教授、博士研究生導師。主要研究方向為先進成形設備、板材成形新工藝等。鄧超,男,1989年生。燕山大學機械工程學院碩士研究生。楊莉,女，1962年生。燕山大學機械工程學院副教授、博士。孔曉華，男，1983年生。燕山大學機械工程學院博士研究生。王耀華，男，1988年生。燕山大學機械工程學院碩士研究生。

中圖分類號：TG386.1

DOI：10.3969/j.issn.1004-132X.2016.02.018