基于三角級數展開的銑削合力頻譜推導及刀具偏心估算

劉　璨　吳敬權　劉煥牢　譚光宇

廣東海洋大學,湛江,524088

?

基于三角級數展開的銑削合力頻譜推導及刀具偏心估算

劉璨吳敬權劉煥牢譚光宇

廣東海洋大學,湛江,524088

摘要：基于一元切削力機理模型將立銑刀的切削合力分解為公稱力和偏心力，采用周期信號的三角級數展開公稱力和偏心力，得到其諧波幅值和相位的表達式。基于以上表達式,推導出偶數齒刀具偏心力的偶數次諧波幅值為0，三齒刀具偏心力的刀齒頻率諧波幅值也為0。提出了一種用切削合力的主軸和刀齒頻率諧波估算刀具偏心距和偏心角的方法，實驗結果表明,采用該方法計算出的偏心值接近實測值。從理論上證明了偶數齒刀具的偏心力不存在偶數次諧波成分，所提出的估算方法只需一套估算式和一次切削實驗，且數值計算比較容易。研究結果可用于偶數齒刀具的加工過程偏心和磨損辨識及其偏心量估算。

關鍵詞：銑刀;偏心;銑削力;頻譜

0引言

銑刀偏心和刀具磨損都將使各個刀齒的切削力不一致。如Schmitz等[1]指出,偏心距為4.9μm的二齒銑刀兩個刀齒的切削力峰值大致呈倍數關系。卞榮等[2]認為微細銑刀偏心可能導致單齒切削。Zhang等[3]的研究結果表明,磨損刀齒的切削力將增大。銑刀偏心和刀具磨損對切削力的影響有相似之處，為識別刀具過程狀態，有必要提取出偏心的獨有特征，并估算偏心尺寸。

以切削厚度為偏心尺寸的函數，Fu等[4]提出了偏心面銑刀的切削力模型；Zheng等[5]提出了偏心面銑刀傾斜銑削的切削厚度模型；Amarego等[6]提出了偏心立銑刀的切削力模型;Li等[7]提出了考慮螺旋角的偏心立銑刀切削力模型；劉璨等[8]推導出偏心立銑刀切削厚度的一種表達式。基于切削力模型,Kline等[9]發現偏心刀具的切削力主軸頻率成分顯著。Wang等[10]對切削分力作傅立葉變換,發現刀齒倍頻±主軸頻率處的切削分力成分包含偏心信息，并用切削分力的主軸頻率分量和常數項分量估算了偏心尺寸。文獻[11-12]在此方法的基礎上進一步用優化方法尋找最優估算值。這一方法對二齒和二齒以上的刀具采用不同的估算方程式，且難以解釋不同切削分力估算結果的不一致性。Liu等[13]通過模型仿真發現，偶數齒銑刀的偏心力不存在偶數次諧波的現象，并提出了利用這一特點辨識偏心和磨損的新思路，但沒有從理論上給予證明。

本文用三角級數展開的方法得到切削合力的頻譜表達式，進而從理論上證明了Liu等[13]發現的現象，并提出了應用切削合力的主軸頻率和刀齒頻率諧波估算偏心距和偏心角的方法。

1偏心刀具的切削力分解

對于齒數為z的立銑刀，若刀具浸入角不大于2π/z，為單齒銑削。圖1所示為偏心刀具逆銑時切削平面示意圖，其中,O1為主軸旋轉中心，O2為刀具物理中心,O1O2為偏心距ρ,β為刀具浸入角。按切削先后順序對刀齒進行排序，以切削力最大的刀齒為第0刀齒，圖1中T0為第0刀齒。α0為偏心方向與T0的夾角,視作刀具偏心角。

在一個主軸旋轉周期內,第i刀齒切削時的切削厚度表達式[13]為

(1)

φ=α0-(z+1)π/z

(2)

θi=ωst

(3)

式中,h(θi)為第i齒的切削厚度;ft為每齒進給量;θi為第i齒旋轉角;i為刀齒序號,i∈{0,1,…,z-1};ωs為主軸角速度;t為時間變量。

一元切削力模型(lumpedforcemodel)的切削合力與單元刃的切削材料未變形面積成正比。為簡化計算,將各刀刃單元的切削厚度作相等處理，則第i個刀齒切削時的切削合力F(θi)的表達式為

F(θi)≈Kh(θi)az

(4)

式中,K為切削力系數;az為切深。

將式(1)代入式(4),得

F(θi)=FN(θi)+FE(θi)

(5)

(6)

(7)

式中,FN(θi)為公稱力；FE(θi)為偏心力。

公稱力是刀具旋轉角的函數，各刀齒的公稱力都相同，因此，公稱力是以刀齒頻率為頻率的周期信號。就同一次加工而言,α0和z為常值，若切削用量保持不變,則刀齒號i為偏心力的唯一變量,主軸每旋轉一周，刀齒號就變化一個周期，因此，偏心力是與主軸旋轉同頻率的周期信號。若將FE(θi)的系數2Kρaz歸一化為1 N,設α0=-π/6,z=4,β=π/3,則偏心力FE在一個主軸旋轉周期內的波形如圖2所示。

公稱力和偏心力都是周期信號,由多個諧波成分疊加而成，它們可分解為以時間t為變量的公稱力FN(t)和偏心力FE(t)：

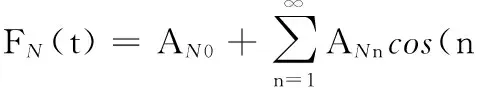
(8)

(9)

其中,AN0、AE0分別為公稱力和偏心力的常數項。ANn、AEn分別為公稱力和偏心力的n次諧波的幅值。n為諧波次數,n為自然數。ωe為公稱力的角速度,等于刀齒頻率。ωs為偏心力的角速度,等于主軸旋轉的角速度。nωe、nωs分別為公稱力和偏心力的n次諧波的圓頻率。φNn和φEn分別為公稱力和偏心力的n次諧波的相位。ωe和ωs的關系為

ωs=zωe

(10)

2偏心刀具的切削合力頻譜表達式、特征

周期信號x(t)可以用三角函數展開式展開：

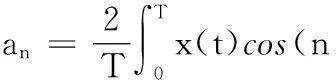
(11)

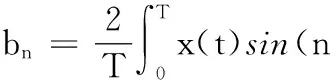
(12)

(13)

φn=arctan(bn/an)

(14)

式中,an、bn為三角函數展開式系數;T為x(t)的周期;ω為x(t)的圓頻率;An、φn分別為x(t)的n次諧波的幅值和相位。

公稱力和偏心力分別是以ωe、ωs為角速度的周期信號，所以可以用三角函數展開式求出其幅值和相位表達式。

2.1公稱力的頻譜表達式

將式(3)和式(6)代入式(11)、式(12)，得

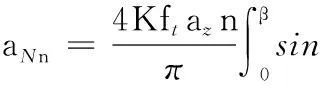
(15)

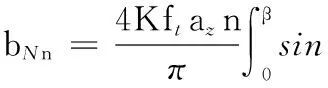
(16)

式中,aNn、bNn為公稱力的三角函數展開式系數。

將式(15)、式(16)代入式(13)、式(14)，得

(17)

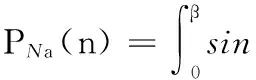
(18)

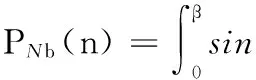
(19)

(20)

式中,ANn、φNn分別為公稱力的n次諧波的幅值和相位。

2.2偏心力的頻譜表達式

Ts為偏心力的周期,即刀齒周期。φEn為偏心力的n次諧波的相位。

將式(7)代入式(11)、式(12)，得

aEn=

(21)

(22)

式中,aEn、bEn分別為偏心力的三角函數展開式系數。

將式(21)、式(22)代入式(13)、式(14)，得

(23)

(24)

(25)

(26)

式中,AEn、φEn分別為偏心力的n次諧波的幅值和相位。

2.3切削合力的頻譜表達式

因為偏心力的均值為0,其常數項為0,即

AE0=0

(27)

偏心力的基頻為主軸頻率,公稱力的基頻為刀齒頻率,切削合力的基頻為主軸頻率。將式(8)、式(9)、式(27)代入式(5)，得

AEncos(nωst+φEn)]

(28)

其中,m=n/z,且m為正整數。式(28)表明，切削合力的常數項等于公稱力的常數項。

若n不為z的倍數,則切削合力的第n次諧波只包含偏心力的第n次諧波，其幅值和相位為AEn和φEn。

若n為z的倍數,則由式(28)可得,切削合力的第n次諧波的幅值An和相位φn的表達式為

(29)

(30)

2.4切削合力的頻譜特征

2.4.1偶數齒刀具

考慮z和n都為偶數的情況，有

(31)

(32)

由式(24)、式(25)可得

(33)

(34)

將式(31)～式(34)代入式(23)，得

AEn=0

(35)

2.4.2三齒刀具

考慮z=n=3的情況,將z=n=3代入式(23)～式(25)，得

AE3=0

(36)

3刀具偏心尺寸估算方法

立銑刀的齒數z通常大于或等于2,由2.3節的分析可知,切削合力的主軸頻率諧波(即1次諧波)等于偏心力的1次諧波。切削合力的n次諧波等于公稱力的1次諧波和偏心力的n次諧波之和。可用切削合力的主軸頻率諧波(即1次諧波)和刀齒頻率諧波(即n次諧波)的幅值和相位代入式(17)～式(20)、式(23)～式(26)、式(29)、式(30)，再采用方程式求解的數值方法求出偏心距ρ和偏心角α0的值。具體估算方法如下：

(1)在銑削過程中采集各切削分力，合成為切削合力。

(2)對切削合力應用FFT算法，求切削合力主軸頻率諧波的幅值A1和相位φ1，以及刀齒頻率諧波的幅值An和相位φn,AE1=A1,φE1=φ1。

(3)將φ1的值代入式(2)、式(24)～式(26)，求出偏心角α0。

(4)將An、φn的值代入式(17)～式(19)、式(23)～式(25)、式(29)～式(30)，求出偏心距ρ。

根據2.4節的分析結果,對于偶數齒和三齒刀具,其偏心力不存在刀齒頻率諧波，即AEz=0,可大大簡化偏心距ρ的計算,因此,偶數齒和三齒刀具的偏心尺寸的計算較簡單。

4實驗

用φ10mm四齒硬質合金立銑刀在銑削加工中心上切削45鋼材料。用北京航空航天大學SDC-C4F測力系統(包括應變式測力儀、應變放大器和測力軟件)同時測量三個切削分力,測力系統的靈敏度為133.33N/V。逆銑，空氣冷卻，切削寬度為5mm,主軸轉速為1836r/min，進給量和切削深度變化，采樣頻率為4896Hz。切削參數列于表1。用千分表測得刀具靜態偏心距約5.0μm,靜態偏心角約45°。

可計算出實驗的主軸旋轉頻率為30.6Hz,4倍頻(刀齒頻率)為122.4Hz。由實驗的加工參數可知,β≈45°。

將實測切削分力合成為切削合力。經濾除50Hz電磁噪聲和高于325Hz的成分后，切削合力數據如圖3～圖6所示。

對各次實驗的切削合力數據作快速傅里葉變換處理,得到切削合力的幅頻譜和相頻譜,其中5號實驗的頻譜如圖7所示。得到各次實驗的切削合力的1次諧波的幅值A1、相位φ1以及4次諧波的幅值A4,見表2。

由上文的分析結果可知，A1=AE1,φE1=φ1,A4=AN1。由式(2)、式(17)～式(19)、式(23)～式(26)計算得到各次實驗的偏心距和偏心角的估算值，見表2。

5探討與結論

5.1探討

如表2所示,當進給量或切削深度較小時，用估算得到的偏心距偏小，這可能是尺寸效應所引起的。本文的估算方法基于切削力系數K為常數,而當進給量或切削深度較小時K不為常數,因此,本文的估算方法適合采用較大的進給量和切削深度。

因偏心力不存在常數項，則A0=AN0,由AE1和A0可求得偏心距ρ的值。對于奇數齒刀具，這種方法比前述方法的計算更簡單。然而，切削力系數的尺寸效應對切削合力常數項的作用較大，用該方法將有更大的估算誤差。

Wang等[10]也采用了公稱力和偏心力頻譜的方法估算銑刀偏心尺寸,然而,該方法基于二元切削力機理模型和傅里葉變換,采用x或y向切削分力的常數項和1次諧波估算。而本文的方法基于一元切削力機理模型和周期信號的三角函數展開式，采用切削合力的1次和n次諧波估算。與Wang等[10]的方法相比,本文的方法可降低切削力系數尺寸效應對估算結果的干擾，并且二齒及以上刀具的估算式唯一。

為便于闡述，本文以切入角為0、切出角為β的逆銑為例說明理論推導過程。對于任意的切入角θ1、切出角θ2以及順銑，都有同樣的推導結果，在計算時，用具體的θ1和θ2替代0和β。

5.2結論

(1)由式(35)、式(36)可知，偶數齒刀具和三齒刀具的偏心力的偶數次諧波為0,表明偶數次諧波不存在，這從理論上支持了文獻[13]的仿真和實驗結果。

(2)從表2可見，各次實驗的偏心角估算值之間的偏差小于10°，且與靜態偏心角實測值的偏差較小，表明本文提出的立銑刀偏心角估算方法在實驗參數范圍內有效。

(3)從表2可見，各次實驗的偏心距估算值與靜態偏心距實測值的相對偏差較小，表明本文提出的立銑刀偏心距估算方法在實驗參數范圍內有效。

(4)偶數齒刀具的偏心尺寸計算較簡單，此外，考慮到尺寸效應的影響，本估算方法更適用于偶數齒刀具，且適合采用較大的進給量和切削深度。

參考文獻:

[1]SchmitzTL,CoueyJ,MarshE,etal.RunoutEffectsinMilling:SurfaceFinish,SurfaceLocationError,andStability[J].Int.J.Mach.Tools&Manuf.,2007,47(5):841-851.

[2]卞榮, 何寧, 李亮, 等. 微細銑削氧化鋯陶瓷銑削力特征分析[J]. 中國機械工程, 2014, 25(23): 3200-3206.

BianRong,HeNing,LiLiang,etal.AnalysisonCharacteristicsofMillingForceinMicro-millingofZrO2Ceramics[J].ChinaMechanicalEngineering,2014,25(23):3200-3206.

[3]ZhangS,LiJF,SunJ,etal.ToolWearandCuttingForcesVariationinHigh-speedEnd-millingTi-6Al-4VAlloy[J].InternationalJournalofAdvancedManufacturingTechnology,2010,46(1/4): 69-78.

[4]FuHJ,DevorRE,KapoorSG.AMechanisticModelforthePredictionoftheForceSysteminFaceMillingOperations[J].ASMEJ.Eng.Ind.,1984,106(1):81-88.

[5]ZhengHQ,LiXP,WongYS,etal.TheoreticalModelingandSimulationofCuttingForcesinFaceMillingwithCutterRunout[J].Int.J.Mach.Tools&Manuf.,1999,39(12):2003-2018.

[6]AmaregoEJA,DesphandeNP.ComputerizedPredictiveCuttingModelsforForcesinEndMillingIncludingEccentricityEffects[J].AnnalsofCIRP,1989,38(1):45-49.

[7]LiXP,LiHZ.TheoreticalModelingofCuttingForcesinHelicalEndMillingwithCutterRunout[J].InternationalJournalofMechanicalSciences,2004,46(9):1399-1414.

[8]劉璨,吳敬權,李廣慧,等.基于單刃銑削力峰值的銑刀偏心辨識[J].機械工程學報, 2013,49(1):185-190.

LiuCan,WuJingquan,LiGuanghui,etal.IdentificationofMillsEccentricityBasedonPeakForceofSingleEdge[J].JournalofMechanicalEngineering,2013,49(1):185-190.

[9]KlineWA,DevorRE.TheEffectofRunoutonCuttingGeometryandForcesinEndMilling[J].Int.J.Mach.ToolDes. &Res.,1983,23(2/3):123-140.

[10]WangJJJ,ZhengCM.IdentificationofCutterOffsetinEndMillingwithoutaPriorKnowledgeofCuttingCoefficients[J].InternationalJournalofMachineTools&Manufacutre,2003,43(7):687-697.

[11]WanM,ZhangWH.SystematicStudyonCuttingForceModelingMethodsforPeripheralMilling[J].Int.J.ofMach.Tools&Manuf.,2009,49(5):424-432.

[12]劉顯波, 龍新華, 孟光,等.基于頻域多目標優化的銑削力系數及偏心參數識別[J].機械工程學報, 2011,47(7):185-190.

LiuXianbo,LongXinhua,MengGuang,etal.TheIdentificationsofMillingForceCoefficientsandEccentricityBasedonMulti-objectiveOptimizationinFrequency-domain[J].JournalofMechanicalEngineering,2011,47(7):185-190.

[13]LiuC,WuJQ,LiGH,etal.Frequency-spectrumCharacteristicsofForceinEndMillingwithToolWearandEccentricity[J].Int.J.Adv.Manuf.Technol.,2013,67(1/4):925-938.

(編輯陳勇)

SpectralDerivationofResultantMillingForceandEccentricEstimationofToolBasedonTrigonometricSeriesExpansion

LiuCanWuJingquanLiuHuanlaoTanGuangyu

GuangdongOceanUniversity,Zhanjiang,Guangdong,524088

Keywords:millingcutter;eccentricity;millingforce;frequencyspectrum

Abstract:Thecuttingforcewasdiscomposedintonominalandeccentriccomponentforcesbasedonunarycuttingforcemodel,thetrigonometricseriesofperiodicsignalswasappliedtoexpandthesetwocomponentforces，andthentheamplitudeandphaseexpressionsoftheirharmonicswereobtained.Basedontheseexpressions,itisdeducedthattheeven-harmonicsamplitudesoftheeccentricforceforeven-toothmillingcutterarezero,thetooth-frequencyamplitudeoftheeccentricforcefor3teethmillingcuttersiszerotoo,andanewestimationmethodofeccentricdistanceandangleformillingcutterswaspresented,whichusestheharmonicsofresultantcuttingforceinspindleandtoothfrequencies,theestimatedeccentricvaluesareclosetothatmeasuredinexperiments.Ittestifiesintheorythattherearenoevenharmonicsintheeccentriccomponentforceofeven-toothmillingcutters,thepresentedmethodneedsonlyonesetofequationandonecuttingtest,anditsnumericalcalculationisrathereasyforeven-toothmillingcutters.Theresearchfruitscanbeusedtoidentifyeccentricityandwear,andestimateeccentricityinprocessforeven-toothmillingcutters.

收稿日期：2015-04-14

基金項目：國家自然科學基金資助項目(51375099，51375100)

作者簡介：劉璨，男，1971年生。廣東海洋大學工程學院副教授、博士。主要研究方向為機械加工過程的監測控制。吳敬權，男，1980年生。廣東海洋大學工程學院實驗員。劉煥牢，男，1967年生。廣東海洋大學工程學院教授、博士。譚光宇(通信作者),男,1957年生。廣東海洋大學工程學院教授、博士。

中圖分類號：TH161

DOI：10.3969/j.issn.1004-132X.2016.02.017