“雞兔同籠問題”教學實踐與思考

王來波

【摘 要】從規律學習的角度，對“雞兔同籠問題”進行深入思考，發現其核心是“調整替換”，“雞兔同籠問題”是一個動態的、變化的規律。文章在遵循規律學習路徑的基礎上展開教學，將“雞兔同籠問題”中的3種方法與規律學習路徑進行有機結合，促使學生有效建模。

【關鍵詞】規律學習；雞兔同籠；調整替換

中圖分類號：G623.56 文獻標識碼：A 文章編號：1671-0568（2016）18-0092-03

“雞兔同籠問題”是我國古代數學名著《孫子算經》中記載的一道數學趣題，其解法之多、思想之廣、變式之靈活是眾所皆知的。正因為如此，這節課的教學方式豐富多彩，在名師展示的舞臺上更演繹出多種方法，有的側重于畫圖，認為這是最直觀、最容易理解的方法；有的側重于列表，認為學生有列表的經驗；有的側重于假設，認為假設法書寫簡潔方便。如今，該內容已經出現在新版四年級數學教材中，而且將方程的解法置之度外，其難度可想而知。那么，這節課如何教學呢？

筆者認為，“雞兔同籠問題”看似是3種不同的方法，但其本質都是“調整替換”。追尋本源發現，“雞兔同籠問題”中隨著雞的數量逐一增加，雞和兔腳的總數按2只遞減。正是由于這一基本變化規律，很容易得出結論：如果腳減少2只，應該將1只兔換成1只雞。反之，腳增加2只，應該將1只雞換成1只兔。在小學數學中，探索規律是讓學生在給定的事物中發現、探求隱含的規律或變化趨勢，而“雞兔同籠問題”就是要通過畫圖、列表、算式等方法，讓學生經歷“初步感知規律、發現形成規律、應用規律”這樣的過程，因而本節課的教學實質是規律教學，應該納入規律教學的范疇，需要走規律教學的路徑，其3種方法的教學缺一不可。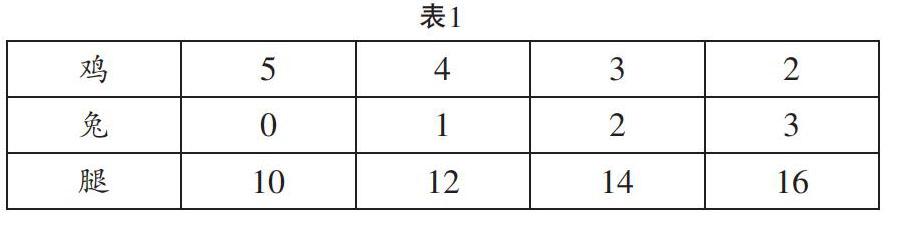

一、畫圖法——初步感知規律

規律是指事物之間的內在本質聯系，是客觀存在的，不以人們的意志為轉移。找規律重在“找”，學生通過自主探索、動手操作來感知內在聯系。教學“雞兔同籠問題”時，可用畫圖法來“找”規律、感知規律，這是規律教學的著力點。教學前，筆者先進行前測。前測題如下：

1. 雞兔同籠，從上面看共有3個頭，從下面看共有16條腿，雞、兔有幾只？

2. 雞兔同籠，從上面看共有8個頭，從下面看共有26條腿，雞、兔各有幾只？

據統計，一共收到52份前測卷，用畫圖解決的有35人，列算式的3人，列表的1人。第一題做對36人，第二題做對28人。顯然，畫圖是學生最喜歡用的方法，正因為學生有這樣的經驗，為“雞兔同籠”的規律教學奠定了基礎。雖然學生呈現的靜態圖一樣（見圖1），但在畫的過程中想法是不一樣的。筆者訪談了幾位學生，發現學生的方法不一：有的毫無計劃性，雞畫幾只，兔畫幾只，最后調整；有的對半分開畫，先畫雞兔各半，再調整；還有的先全部畫雞，多出來的腿按2條一組添上去變成兔。雖然學生畫的方法不一樣，但他們都經歷了“調整替換”的過程。畫圖是最直觀的解題方法，旨在通過畫圖中的有序思考發現、形成規律，并嫁接起列表法、假設法，教師必須放慢腳步，讓學生都來講講自己的畫法，在聆聽別人有序思考的基礎上初步感知規律，提升思維品質。

【教學片斷】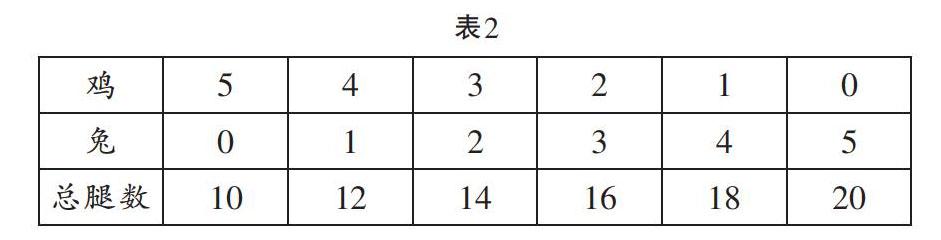

師：畫出來的結果都是這樣的，可畫的過程不一樣。

（畫法1：全是雞，一生畫并講解。）

師：再加2條腿，這只雞發生了什么變化？

（畫法2：全部是兔，或者是4只雞、1只兔）讓學生選擇一種喜歡的畫法，與同桌交流。

師：其實，還有很多畫法，有的學生直接畫成2只雞、3只兔，或者3只雞、2只兔，腿數不對再調整。像這樣的畫法就是先假設再調整，有的學生一次性替換，也有的逐只替換。

通過對前測中學生不同畫法的交流，可以發現學生對“雞兔同籠問題”的內在規律已經有了初步感知，替換一次多（少）2條腿。教師不能只教會學生一道題的解題思路和方法，而是要通過一道題類推到一類題，做到舉一反三、觸類旁通，幫助學生建立“雞兔同籠問題”的模型。例如，學生熟悉的摩托車和小汽車問題、龜鶴問題等，都與雞兔問題模型完全一致，能夠使學生很好地建立起聯系。此外，讓學生通過畫圖感知“相差數都是2”，所以，調整替換的時候是2條腿。當變式“相差數是1”時，學生理解就有困難。筆者特意在解決摩托車和小汽車問題后設置三輪車和小汽車的問題，讓學生先畫一畫，充分感知“相差數是1”的規律，畫圖能讓學生非常直觀地感知到“調整替換”的就是兩個量的差，它是根據情境變化而變化的。

學生已經有了畫圖找規律的經驗，而“雞兔同籠問題”中頭數與腿數的變化規律隱含在替換過程中，學生通過畫圖才能直觀感知內在規律。所以，通過畫圖，可以幫助學生感知“雞兔同籠問題”用相差數替換的規律、發現形成規律、發展形象思維能力。

二、列表法——發現形成規律

列表能清晰地表示兩個量之間的數量關系，在變與不變中發現規律。從直觀的畫圖到半抽象的列表，有利于學生發現、形成規律。通過畫圖，學生對“雞兔同籠問題”的規律已經有了初步感知，但此時的感知是粗淺的、零散的，需要整理、對比、分析，才便于學生發現形成規律。

表格中的數據相對抽象，學生理解有一定難度，尤其是不明白每個數據表示的意思，見表1。相互交流時，很多學生一臉茫然，不知所云。于是，筆者拿出雞和兔的若干圖片，讓學生用調整替換的思想來擺一擺、說一說，在操作中感知替換的過程。

表1

【教學片斷】

師：大家能理解這個方法嗎，第一列是什么意思呢？老師今天特意把兔和雞都請來了，看看它們怎么變化。

生：把它們全部想成雞，5個頭，每只雞2條腿，一共10條腿。

師：想一想，這時腿發生了怎樣的變化？

生：……

師：是啊，其實就是用兔子換了這只雞，每換1只雞，多了……

生：2條腿。

師：這個時候，雞其實就是變成了……

生：兔。

師：一直到換到16條腿，為什么不再換下去了？

生：……

就這么簡單的擺一擺、換一換，將表中每個數據的含義詮釋得一清二楚，尤其是讓學生發現了鄰近兩列數之間的變化規律：每換1只兔子就多了2條腿，真正理解了“2”表示的意義，它并非是雞的2條腿，而是1只雞和1只兔腿的差。這個替換的過程在畫圖時學生有了初步感知，但還有部分學生一知半解。因為畫的時候學生只關注腿的數量，而忽視了頭的變化。所以，將靜態的數據用動態的操作去支撐，更有利于對規律的理解，更有利于模型的建立，有利于學生逐步發現規律。除了理解表格中每個數據的含義，以及鄰近兩列數字的變化規律還不夠，學生只理解了逐只調整替換的過程，無法與一次性替換的畫法有效嫁接。所以，應在學生基本理解列表法的基礎上完成表格，并對表格進行再度挖掘，引導學生發現規律。

【教學片斷】

師：你能從表2中看到第一個同學的畫法嗎？

生：先全部畫雞，一共10條腿，發現還多6條腿……多了6條腿，要把3只雞替換成兔。因為每換1只多2條腿。

師：誰上來指一指，他講的是哪兩列數之間的關系？能從表2中看到其他畫法嗎？

生：……

表2

在這節課中，列表法并不是孤立的，它是在學生通過畫圖初步感知規律的基礎上發現形成規律的過程，這是必不可少的方法。1張表格由于觀察角度不同，學生看到的調整替換過程也不同，應引導學生與畫法相聯系來分析表格中的數據，看懂每一種畫法，為弄清抽象規律、應用規律奠定基礎。在教學中，不僅要讓列表法與畫圖法相聯系，便于學生更好地理解列表法，還要讓列表法與假設法相聯系，為學生學習假設法打好基礎，成為發展學生思維能力的載體。

三、假設法——應用規律

學生對數學規律的學習，除了感知規律、發現形成規律外，更重要的是能運用規律解決一些實際問題。當“雞兔同籠問題”涉及的數據越來越大、越來越復雜的時候，學生越來越感覺到畫圖法和列表法的繁雜，同時，他們對其中的規律已經明晰，這時假設法便應運而生。運用假設法解決“雞兔同籠”問題，學生不難總結出如下規律：雞的只數=（頭的總個數×4-腳的總只數）÷（4-2），兔的只數=（腳的總只數-頭的總個數×2）÷（4-2）。運用這個數學模型，可以快速解決類似問題。數學建模是解決實際問題的一種思考方法，數學教師有責任讓學生學習和初步掌握數學建模的思想方法，從而更積極、主動地學習數學，使學生終身受益。

【教學片斷】

師：大家看，摩托車和小汽車其實與“雞兔同籠問題”類似。停車場有摩托車和小汽車共35輛車，（ ）個輪胎，摩托車和小汽車各有幾輛？輪胎數據就在下面3個數據之中：A. 56；B. 160；C. 94，你會選哪個？

生：A太少，如果全是摩托車，就有70個輪胎；B太多，如果全是汽車，最多140個輪胎。

師：也就是說，這個輪胎的數量比70多，比140少，于是選C。你們想到了剛才那道題目嗎？籠子里有若干只雞和兔，從上面數，有35個頭；從下面數，有94只腳。雞和兔各有幾只？它們有什么相同之處？

教師呈現算式，學生寫單位名稱。

摩托車和小汽車的問題正好與“雞兔同籠問題”的模型完全一致，能夠使學生很好地建立起聯系。其中，對輪胎數的選擇是學生進一步理解假設法的本質所在，并滲透極限思想，形成一定的區間意識。解題過程并非教學難點，填寫正確的單位名稱、區分兩個未知量才是困難所在。如果能正確填寫，也就意味著模型基本形成。替換過程仍按2個進行變化，因為兔和雞的腿相差數量是2，而小汽車和摩托車輪子的數量也相差2，真正建模必須打破這一思維定式。于是，筆者緊接著安排了另一題：停車場有摩托車和三輪車共8輛，20個輪胎，摩托車和三輪車各有幾輛？”反饋時和第一題進行比較，重點提問：“為什么剛才都是除以2，現在除以1？”并順勢提問：“三輪車和小汽車除以1，還想到了什么？”將學生的思維引向更深處。

規律學習的過程離不開初步感知、發現形成、運用規律，而“雞兔同籠問題”的3種解法分別很好地與之對應。因此，上述3種方法缺一不可，不能根據教師的喜好隨意選擇。畫圖法讓學生在畫的過程中充分感知“替換調整”的規律；列表法讓學生將規律用半抽象的數據進行呈現，發現形成規律；假設法能使學生應用規律解決一些實際生活問題。真正的教學，要還學生一個思維的舞臺，且循著規律教學的路徑，才能使學生獲得知識與技能，積累一定的基本活動經驗，感悟數學思想，提升思維品質。

（編輯：易繼斌）