例談模考卷幾何綜合題的命制

☉江蘇省鹽城市初級中學　陳冠軍

?

例談模考卷幾何綜合題的命制

☉江蘇省鹽城市初級中學陳冠軍

一、寫在前面

中考模考卷往往發揮著考生參加中考前的熱身、適應、評估的作用.本文呈現的是我在某次模考卷命題過程中對一道幾何綜合題命制的思考與體會，現成文如下，供分享和研討.

二、一道幾何綜合題的命制歷程

（一）考題原型

（一道八年級試題）如圖1，在正方形ABCD中，E是BC上一點，F是AE上一點，過點F作GH⊥AF，交直線AB 于G，交直線CD于H.

（1）求證：BG=CH-BE；

（2）如圖2，若F是AE延長線上一點，其余條件不變，試探究：BG、BE、CH之間的數量關系；

（3）如圖3，若K為CD邊上一點，AD=3，∠DAK=30°，M為AK的中點，過點M的直線分別交邊AD、BC于P、Q點，且PQ=AK，則AP的長為多少？

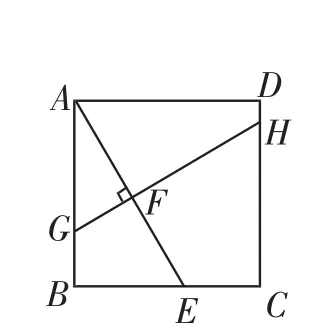
圖1

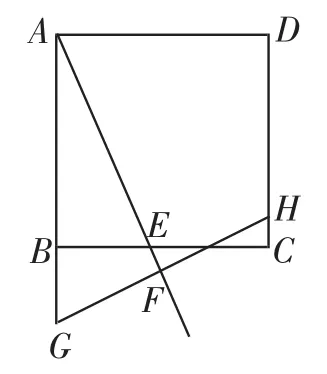
圖2

圖3

思路簡述：前兩問比較簡單，屬于常規題，第三問有一定的難度，筆者曾預設制作了如圖4所示的PPT，在八年級講評該題.

圖4

經過圖4這樣的動畫漸次呈現思路啟發，并追問學生的理解之后，取得了較好的教學效果.從命題角度看，前兩問“相聚”在題干下是恰當的，而第三問與題干中的條件和信息無關，屬于獨立問題，沒有必要作為該題的（3），特別是第三問中的圖形并不需要給出，條件敘述得很清楚，圖形應該由練習者自己構造.這樣的解題教學、命題反思過程啟發筆者在接下來的模考題命制中生成幾何綜合題的初稿.

（二）幾何模考題命制歷程

第1稿：如圖5，點E為正方形ABCD的邊AD上一點，連接BE，∠AEB=60°.

（1）利用尺規作圖補全圖形.（要求：保留作圖痕跡，并簡述作圖步驟）

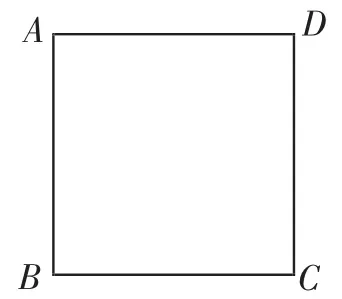
圖5

（2）取BE的中點M，過點M的直線交邊AB、CD于點P、Q.

①當PQ⊥BE時，求證：BP=2AP；

設計意圖：這道綜合題主要受到“原型問題”的第三問啟發，融入尺規作圖，讓學生作出點E，并繼續引導研究相關問題，后兩問之間緊密聯系，逆向設問，但又需要考慮分類討論，如圖6，需要考慮PQ、P′Q′兩種不同位置關系，相應的△BPM就有兩種不同的解.

圖6

但考慮到作為全卷倒數第2題，最后一問的難度還偏低，不足以滿足“高層次”學生的區分作用，故打磨成第2稿.

第2稿：（限于篇幅，前面不變，只是將最后一問更改如下）

②小舟同學發現：當PQ=BE時，點Q、D、E、M在同一個圓上，請判斷“小舟的發現”是否正確，并說明理由.

設計意圖：將問題解題視角向四點共圓拓展，追求較高的拓展和生長，但考慮到《課標（2011年版）》弱化了圓的學習與考查要求，故還是放棄四點共圓的拓展，打磨成第3稿.

第3稿：（限于篇幅，前面不變，只是將最后一問更改如下）

②當PQ=BE時，延長BE、CD交于N點，猜想NQ與MQ的數量關系，并說明理由.

設計意圖：通過延長BE、CD，增加解題層次，需要分類討論、猜想數量關系，并說明理由，應該能達到較好的區分功能.但是命題組有老師認為題干的表述不太自然，于是我們重新表述題干后，定稿如下.

定稿：如圖5，四邊形ABCD為正方形.在邊AD上取一點E，連接BE，使∠AEB=60°.

（1）利用尺規作圖補全圖形.（要求：保留作圖痕跡，并簡述作圖步驟）

（2）取BE的中點M，過點M的直線交邊AB、CD于點P、Q.

①當PQ⊥BE時，求證：BP=2AP；

②當PQ=BE時，延長BE、CD交于N點，猜想NQ與MQ的數量關系，并說明理由.

接下來是整理參考答案與制訂評分標準：由于評分標準常常不為有些命題老師所重視，使得閱卷時造成評分隨意，不能準確體現試題的診斷、評估功能，故這一環節在命題過程中也是十分重要的，以下給出我們制定的簡要評分說明.

（1）如圖7，分別以點B、C為圓心，BC長為半徑作弧，交正方形內部于點T，連接BT并延長交邊AD于點E……3分

圖7

★評分提醒：該題的作法眾多，估計學生會有n種成功作法，評卷老師注意結合考生的作圖語句敘述仔細辨認，慎重評分.命題意圖是引導學生重視古老的尺規作圖及其背后的理由，平面幾何的理性思維的價值也在于此，這也是《課程標準（2011年版）》上所倡導的.

（2）這里證明是常規思路，為節約篇幅不展示.

（3）需學生考慮兩種情形（如圖8、9），分析出NQ= 2MQ或NQ=MQ.

圖8

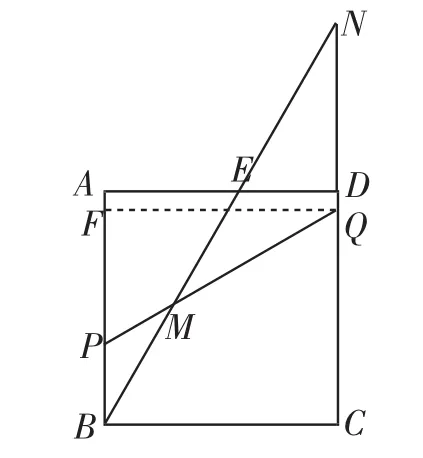
圖9

三、命題反饋與辯護

考試之后，我們收集了一些反饋意見，比如有人認為：覺得第一問的起點有些高，打著尺規作圖的幌子其實是個腦筋急轉彎，而且從最近幾年的中考看，雖然在考試范圍內，但尺規作圖一直沒有怎么考過.很多學生說＂死在第一問＂上，于是就都空白了.

作為命題人，給出一些辯護：覺得到了第27題（全卷倒2的位置），“很多學生”應該“有為有不為”，可能并不適合他們……如果智慧一點，懂得取舍，可能會搶到第二問的分，同時還會啟發他們做第一問、第三問的一半.臨近中考，應試策略與機智往往區分了學生的能力.當然，如果是高利害的中考試卷，確實要適當降低起點.作為模考題，主要基于如下考慮.

第一，尺規作圖及作法在課標中明確要求，應該值得教學重視，這是幾何教學的重要價值.另外就尺規作圖來說，基本作圖的適當變式、草圖分析等都盡顯智慧，且這是第27題，并不是第20題的位置，考生應該有心理準備.

第二，對于第一問做不出來的考生，即將參加中考，仍不知道“跳步解答”（羅增儒語），這說明備考策略、應試策略還有很多要做的事……

第三，如果懂得跳步解答，先做后面的設問，也許會反過來提醒自己第一問的作圖本質，把智慧數學或數學中的智慧理解成腦筋急轉彎，只能說考生對問題缺少深入思考，沒有揭示或洞察問題的深層結構.

第四，本題幾個設問，命題技術上只是玩了一個“多元表征”理論.

四、寫在最后

寫文章、創作詩詞，最怕的是無厘頭的語句、段落，那么命題領域，這種現象廣泛存在……很多命題人以為只要把幾個小問湊在一個問題下就完事，其實拼湊取向、個人的旨趣，影響了數學的面貌，只會讓練習者討厭數學，問題很大……數學命題的專業隊伍建設之路漫漫.當然，上乘的命題藝術，一如繪畫、詩詞，前后看似毫無關聯，卻于留白處引人入勝，并會遇到知音、引發共鳴.

參考文獻：

1.羅增儒.數學解題學引論［M］.西安：陜西師范大學出版社，2008.

2.中華人民共和國教育部制定.義務教育數學課程標準（2011年版）［M］.北京：北京師范大學出版社，2012.

3.劉東升.經歷問題生成，深刻理解教材——人教八上“每日一題”的命題實踐與思考［J］.中學數學（下），2014（4）.

4.劉東升.以本為本：習題變式的視角與可能［J］.中小學數學（初中），2016（1）.Z