巧用“1”解不等式

☉湖北省武漢二中 黃亦達

巧用“1”解不等式

☉湖北省武漢二中 黃亦達

不等式在數學研究和數學應用中起著重要作用，高中數學“課標”要求會用基本不等式解決簡單的不等式問題，由于基本不等式既具有定性功能，又具有定理功能，還具有工具性的作用，應用面非常廣泛，涉及高中數學各分支內容，因此在每年高考試卷中出現頻率特高，可以說是每年高考的必考點.但是同學們利用基本不等式解題時，對部分題型已知條件中出現“1”情況如何進行代換，應用上還存在困惑.本文結合常見問題進行了分析和解答，希望能幫助同學們理解和掌握相關的知識.

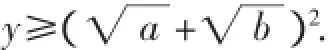
分析：為對（x+y）配式，根據1乘以任何一個式子大小不變，可將1整體代換，從而湊出定積的條件.

【針對練習】已知a＞0，b＞0，c＞0，且a+b+c=1.

分析：為對左式進行變換，可將各分式的分子中的1用a+b+c來代換.

證明：因為a＞0，b＞0，c＞0，且a+b+c=1，

根據不等式性質，得

分析：為了挖掘出定積的情況，根據“1乘以任何一個式子大小不變”，利用代換法，變換所求式子，可得到定積條件.

解答：因為a＞0，b＞0，且a+2b=1，

當且僅當a2=2b2，即當時，取最小值

例3已知a＞0，b＞0，c＞0，且abc=1.求證：（a+1）（b+1）（c+1）≥8.

分析：左邊是3個因式的乘積，右邊是數字，結合已知條件abc=1，如果能將左邊轉化為abc的乘積，根據“1的n次方仍是1”，問題就能解決.

由不等式的性質，得

因為abc=1，所以（a+1）（b+1）（c+1）≥8，

當且僅當a=b=c=1時等號成立.

針對練習：已知a＞0，b＞0，c＞0，且abc=1.證明

分析：左邊是根式，右邊是分式，結合已知條件，根式中每項除1，根式大小不變，再由基本不等式，去掉根號，轉化為分式，問題就能解決.

證明：因為a＞0，b＞0，c＞0，且abc=1，

當且僅當a=b=c=1時等號成立.Z