關于矩陣的Frobenius內積的一個推廣*

劉燕秋, 余 波

( 三峽大學 理學院, 湖北 宜昌 443002)

關于矩陣的Frobenius內積的一個推廣*

劉燕秋, 余 波

( 三峽大學 理學院, 湖北 宜昌 443002)

推廣了矩陣的Frobenius內積的定義, 并在新的矩陣范數意義下, 證明了其矩陣空間是一個嚴格凸的賦范線性空間.

矩陣空間; 向量內積; 矩陣內積

0 引言

矩陣的Frobenius內積是線性代數中的一個基本概念,在很多領域都有廣泛的應用.這些經典的應用包括凸優化以及對稱半正定矩陣的規劃問題,[1-2]求解對稱矩陣特征值的界的問題[3]以及對對稱矩陣的反特征值的數值算法設計[4]等等.近年來,有學者利用矩陣的Frobenius內積定義了旋轉矩陣群上的平均,[5]用奇異值分解方法和關于Frobenius內積的正交補方法刻畫了Moore-Penrose逆的推廣.[6]根據矩陣的Frobenius內積可以誘導出矩陣的Frobenius范數,矩陣的Frobenius范數一樣應用廣泛.比如,有學者利用矩陣的Frobenius范數定義了一類子空間上的矩陣反問題,[7]討論了矩陣方程Ax=B的反對稱正交對稱解的存在性的充要條件,[8]刻畫了稀疏矩陣的低秩逼近的誤差分析,[9]以及按照矩陣的Frobenius范數定義的度量研究了不足采樣下的低秩矩陣重構問題[10]等等.

鑒于矩陣的Frobenius內積和范數的重要性,在1960年,有學者曾將矩陣的Frobenius內積推廣到了更一般的代數結構上去.[11]本文將基于矩陣的Frobenius內積的定義方法, 引入一個m×m階的對稱正定矩陣C, 并利用C定義一個新的矩陣內積. 當C退化為m階單位矩陣時, 此推廣的矩陣內積便為傳統意義下的Frobenius內積. 根據推廣的矩陣內積可以誘導出相應的矩陣范數, 并可以證明賦予該范數的矩陣空間為嚴格凸的.

1 新的定義及預備知識

首先推廣向量的內積.

定義1 設C是給定的m×m對稱正定矩陣. 在實數域R上的m維向量空間Rm中, 對于任意的兩個向量x=(x1,x2,…,xm)T,y=(y1,y2,…,ym)T, 我們定義〈x,y〉C=xTCy為向量x和y關于C的一個關系.

下面我們證明上述關系滿足內積的要求.

定理1 設x,y,z∈Rm,c為任意實數, 則定義1中的關系滿足如下性質:

1)交換律: 〈x,y〉C=〈y,x〉C;

2)齊次性:〈cx,y〉C=c〈y,x〉C;

3)分配律: 〈x+y,z〉C=〈x,z〉C+〈y,z〉C;

4)非負性:〈x,x〉C≥0且〈x,x〉C=0當且僅當x=0.

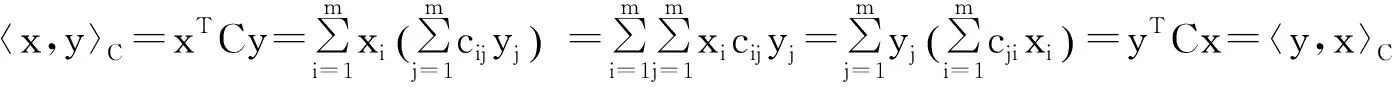
2)〈cx,y〉C=(cx)TCy=cxTCy=c〈y,x〉C.

3)〈x+y,z〉C=(x+y)TCz=(xT+yT)Cz=xTCz+yTCz=〈x,z〉C+〈y,z〉C.

4)由C的正定性易見, 〈x,x〉C=xTCx≥0且xTCx=0當且僅當x=0. 證畢.

根據定理1, 可以看到(Rm,〈·,·〉C構成了一個內積空間. 類似的, 我們可以定義矩陣空間Rm×n上的一個關系.

定義2 設C是給定的m×m的對稱正定矩陣.A,B∈Rm×n，我們定義〈A,B〉C=tr(ABTCT)為矩陣A,B關于C的一個推廣的Frobenius關系, 其中tr(·)表示矩陣的跡.

我們將證明推廣的Frobenius關系滿足內積的要求, 為此, 首先回顧如下兩個結果.[12]

引理1 設A∈Rm×n, C為m×m的對稱正定矩陣, 則AAT與CT的乘積的特征值非負.

引理2 若A,B是Rm×m中的對稱半正定矩陣,λ(·)表示矩陣的第i個特征值,i=1,2,…,m,且按遞減順序排列, 那么對任意的r+s≤m-1, 有

λm-r-s(AB)≥λm-r(A)λm-s(B)

(1)

現在可以證明如下定理.

定理2 設A,B,D∈Rm×n,C為m×m的對稱正定矩陣,c為任意實數, 則推廣的Frobenius關系滿足如下性質:

1)交換律: 〈A,B〉C=〈B,A〉C;

2)齊次性: 〈cA,B〉C=c〈A,B〉C;

3)分配律:〈A+B,D〉C=〈A,D〉C+〈B,D〉C;

4)非負性:〈A,A〉C≥0 且〈A,A〉C=0當且僅當A=0.

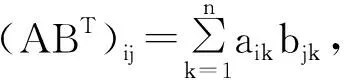
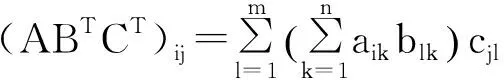
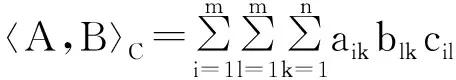
注意到CT=C, 有〈A,B〉C=〈B,A〉C.

2) 設A,B∈Rm×n,C∈Rm×m且CT=C,c為任意常數, 則 〈cA,B〉C=tr(cABTCT)=ctr(ABTCT)=c〈A,B〉C.

3) 設A,B,D∈Rm×n,C∈Rm×m且 CT=C, 則〈A+B,D〉C=tr[(A+B)DTCT]=tr(ADTCT+BDTCT)=tr(ADTCT)+tr(BDTCT)=〈A,D〉C+〈B,D〉C.

4)設A∈Rm×n,C∈Rm×m且CT=C, 則〈A,A〉C=tr(AATCT)≥0. 最后我們運用引理1和引理2來證明〈A,A〉C=0當且僅當A=0. 一方面，A=0當然意味著〈A,A〉C=0. 另一方面,

(2)

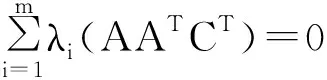
注1：由定理2可知,(Rm×n,〈·,·〉C)構成了一個內積空間. 當m×m的正定矩陣C取為單位陣時, 〈·,·〉C便為傳統意義下的Frobenius(也叫Euclid)內積, 即

〈A,B〉C=tr(ABTCT)=tr(ABT)

(3)

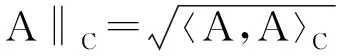
在本節的最后, 我們回顧一個將在下一節中應用的結論.

引理3 設A,B,C∈Rm×m, 則

tr(ABC)=tr(BCA)=tr(CAB).

2 主要結果

下面我們將證明(Rm×n,‖·‖C)為嚴格凸的賦范線性空間. 為了證明這一結果，我們首先回顧如下定義.

定義3 賦范線性空間(Rm×n,‖·‖)稱為嚴格凸的，是指任意A,B∈Rm×n,A≠B必有‖A‖=‖B‖=1,意味著‖αA+βB‖<1(任意α,β>0,α+β=1).

根據此定義可以證明如下結論.

定理3 賦范線性空間(Rm×n,‖·‖C)是嚴格凸的.

證明:我們只要證明對任意A,B∈Rm×n,A≠B必有‖A‖C=‖B‖C=1，意味著‖αA+βB‖C<1(任意α,β>0,α+β=1 ). 反設‖αA+βB‖C=1，由簡單的計算得

‖αA+βB‖C=

(4)

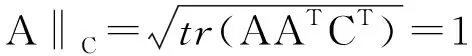
α2+2αβtr(ABTCT)+β2=1

(5)

由α+β=1有

α2+2αβ+β2=1

(6)

將(5)式與(6)式相減得到

2αβ[tr(ABTCT)-1]=0,

因為αβ≠0，所以tr(ABTCT)-1=0,即tr(ABTCT)=1. 因此就有

tr(ABTCT)=tr(AATCT)=tr(BBTCT)=1

(7)

下面我們將分兩種情況證明(7)式蘊含著結論A=B,得到矛盾.

1)若正定矩陣C取為m階單位矩陣，有

tr(ABT)=tr(AAT)=tr(BBT)=1,

設A=(aij)m×n,B=(bij)m×n,

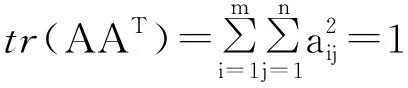
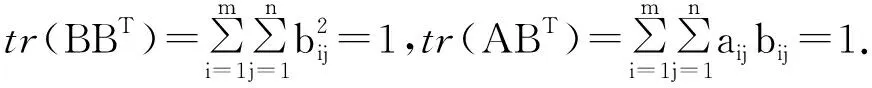
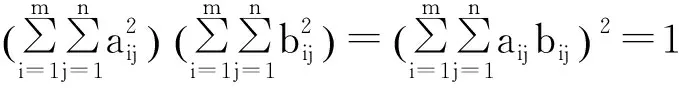
另一方面, 由Cauchy不等式有

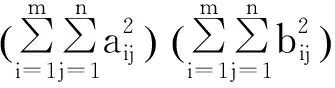
其中等號成立，當且僅當

aij=kbij,i=1,…,m,j=1,…,n

(8)

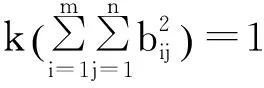
2)若C為一般的m×m正定矩陣, 則存在實可逆m×m矩陣P, 使得PTCTP=E,即CT=(P-1)TP-1.令G=P-1A,H=P-1B,則由引理3有

tr(AATCT)=tr[AAT(P-1)TP-1]

=tr[P-1AAT(P-1)T]=tr(GGT)

(9)

類似地, 有tr(BBTCT)=tr(HHT),tr(ABTCT)=tr(GHT) . 這樣,類似(1)的證明過程可以得到G=H, 即P-1A=P-1B, 因此A=B.

綜合上面兩種情況都可以得到A=B,與條件中A≠B矛盾. 故‖αA+βB‖C<1. 證畢.

[1] Boyd S., Vandenberghe L.. Convex Optimization [M]. Cambridge University Press, 2004.

[2] Alizade F.. Interior point methods in semidefinite programming with application to combinatorial optimization [J]. SIAM. Optim. 1995,5(1):13-51.

[3] Pablo Tarazaga. Eigenvalue estimates for symmetric matrices [J].Linear Algebra Appl., 1990,135:171-179.

[4] Dirk P. Laurie.Solving the inverse eigenvalue problem via the eigenvector matrix [J].J. Comput. Appl. Math. 1991,35: 277-289.

[5] Maher Moakher. Means and averaging in the group of rotations [J]. SIAM J. Matrix Anal. Appl., 2002,24(1):1-16.

[6] Antonio Suarez, Luis Gonzalez. A generalization of the Moore-Penrose inverse related to matrix subspaces of [J].Appl. Math. Comput, 2010,216:514-522.

[7] 袁永新.子空間上的一類矩陣反問題[J].高等學校計算數學學報, 2005,27(1):70-77.

[8] 張宗標.矩陣方程AX=B的反對稱正交對稱解及其最佳逼近 [J].廣西民族大學學報:自然科學版, 2013,19(4):48-54.

[9] Zhenyue Zhang, Hongyuan Zha, and Horst Simon. Low-rank approximations with sparse factors I: Basic algorithms and error analysis [J].SIAM J. Matrix Anal. Appl., 2002,23(3):706-727.

[10] R. Kueng et al., Low rank matrix recovery from rank one measurements [J].Appl. Comput. Harmom. Anal. 2015 , http://dx.doi.org/10.1016/j.acha.2015.07.007.

[11] Ali R. Amir-Moez, Chandler Davis, Generalized Frobenius inner products [J].Mathe. Annalen, 1960:107-112.

[12] Zhang F..Matrix Theory, Basic Results and Techniques [M]. Second Edition, Springer, 2011.

[責任編輯 蘇 琴]

[責任校對 黃招揚]

An Extension of the Frobenius Inner Product for Matrices

LIU Yan-qiu, YU Bo

(CollegeofScience,ChinaThreeGorgesUniversity,Yichang443002,China)

An extension of the Frobenius inner product for matrices is introduced, from which the corresponding norm for matrices is defined. Under this new matrix norm, the matrix space is proved to be a strictly convex normed linear space.

matrix space; inner product for vectors; inner product for matrices

2016-06-20.

國家自然科學基金資助(11301296).

劉燕秋(1991-)，女，三峽大學理學院碩士研究生，研究方向: 逼近論. 通信作者：余波(1979-)，男，博士，三峽大學副教授，研究方向: 計算與應用調和分析,逼近論.

O151.21

A

1673-8462(2016)04-0064-03