基于ARIMA的PPI時間序列分析
耿 強
?
基于ARIMA的PPI時間序列分析
耿強
摘要:ARIMA模型是一類精度較高的時間序列短期預測模型,本文借助于計量經濟學軟件Eviews對我國2010年5月到2012年7 月PPI時間序列數據建立了ARIMA(0,1,1)模型,并對未來我國PPI的走勢進行了預測分析。
關鍵詞:ARIMA模型;PPI;CPI;時間序列分析
一、PPI
PPI即生產者物價指數,也稱作工業品出廠價格指數,是統計部門收集整理的多個物價指數中的其中一個,通常用來衡量制造商出廠價的平均變化的指數,對于市場的敏感度很高。當生產物價指數比預期數值要高時,說明會有通貨膨脹的風險。當生產物價指數比預期數值低的時候,則說明有通貨緊縮的風險。PPI主要目的是衡量商品在不同生產階段價格的變化情況。通常情況下,商品的生產可以分成三個階段:一是原始階段:商品沒有做任何的加工;二是中間階段:商品需要作進一步的加工;三是完成階段:商品不再有任何的加工手續。 PPI之所以重要,是因為PPI是反映某一時期生產領域的價格變動情況的重要經濟指標,是衡量企業產品出廠價格變動程度和變動趨勢的指數,并對制定國民經濟核算和相關經濟政策有重要影響。當前,我國PPI的調查產品大概有4000多種(含規格品9500多種),覆蓋了39個工業行業,涉及的調查種類有186個。
PPI不僅是一個指數,還是一族指數,代表生產中三個漸進過程的每一個階段的價格指數:原材料、中間品和產成品。對金融市場最有影響的就是產成品的PPI。它代表著這些商品被運到批發商和零售商之前的最終狀態。
PPI的計算法則:計算代表規格品的價格指數采用幾何平均法,計算代表產品的價格指數采用簡單算術平均法,計算工業品出廠價格總指數則采用加權算術平均法。
二、CPI與PPI
CPI表示消費者物價指數,它是用來反映居民家庭購買消費商品及服務的價格水平的變動情況,通常作為衡量通貨膨脹的重要指標。
根據價格傳導規律,PPI對CPI也有一定的影響。CPI反映消費環節的價格水平,PPI反映生產環節的價格水平。整體價格的波動首先出現在生產領域,然后通過產業鏈向下游產業擴散,最后會涉及消費品。產業鏈可以分為下面兩條:一是以工業品為原材料的生產,即原材料→生產資料→生活資料的傳導;二是以農產品為原料的生產,即農業生產資料→農產品→食品的傳導。
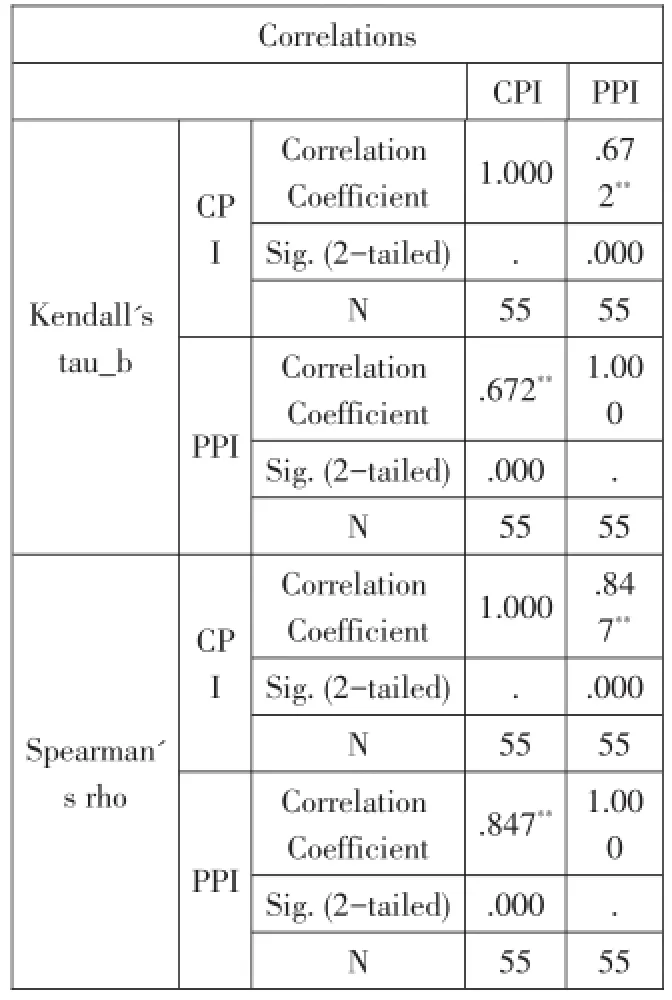
**.Correlation is significant at the 0.01 level(2-tailed).
以上從定性的角度說明CPI與PPI的關系,為了檢驗以上的結論,本文從定量的角度對數據進行分析。選取2008年1月——2012年7月的CPI和PPI數據進行比對。顯示CPI與PPI波動的狀況一致,而且對兩個獨立樣本做非參數與參數檢驗時的p值非常小,說明兩種存在相關關系。相關系數也相對較大,說明PPI與CPI的相關性也很強。
PPI與CPI作為宏觀經濟的兩個重要指標,通常可以根據兩者的走勢了解宏觀經濟狀況。當CPI不斷上漲,而PPI仍然處于企穩或者下跌的時候,經濟就開始步入繁榮期,因為總需求不斷擴張的同時,供給相對充足,此時企業利潤將不斷向上攀升;當CPI開始向下走,而PPI卻不斷向上攀升,此時,經濟就開始步入衰退期,因為CPI的下降表示總需求開始收縮,而PPI的攀升則顯示經濟規模的擴大已經受到上游行業或者資源的約束。
三、基于PPI定性分析
2011年7月,我國的PPI同比增幅一直處于下降趨勢,我們從以下兩方面分析:
一是國外大宗商品價格下降;二是國內通貨膨脹趨于緩和。
2010年開始,我國為了克服通脹,央行持續上調存款準備金,中國經濟處于收縮狀態。并且國內經濟產能出現了嚴重過剩狀況,比如鋼鐵行業。以前中國的重化工業既有海外外需市場的推動,又有國內固定資產投資高速增長的拉動,這樣巨大的需求可以說滿足了中國工業產品供應。隨著金融危機和歐美主權債務危機對中國外需的壓制,中國對房地產進行了宏觀調控,固定資產增速大幅下滑,最終通過PPI的下降和工業增速下降體現出來了。目前來看,短時間內還很難出現改變。
四、建立ARIMA模型
1.數據選取
2010年5月開始,PPI同比增幅呈現下降趨勢。由于采用同比的計算方式,可以忽視季節性的影響因素。
2.對非平穩序列進行平穩化處理
對于非平穩序列,選擇差分法來對確定信息進行提取,是一種非常方便有效的方法。通常差分法的選擇,有以下規律:(1)序列呈現顯著的線性趨勢,通常我們使用一階差分;(2)序列呈現曲線趨勢,則使用低階(二階、三階)差分就能提取出曲線的趨勢;(3)呈現固定周期時,進行步長為周期長度的差分運算。
觀察PPI從2010年5月到2012年7月的時間序列值,可以發現呈現線性趨勢。為了得到平穩的時序,我們對原數據采用一階差分法。差分后的數據dif(x),大致圍繞0.5上下波動,可以大致判斷該時序趨于平穩。繼而再觀察dif(x)的自相關系數,自相關系數ρ快速衰減向0。由于平穩時序通常具有短期相關性,因此隨著延遲期數k的增加,平穩序列自相關系數會快速衰減到0,由此可以認為一階差分后的時序是平穩的。
3.純隨機性檢驗(a=0.05)
如果各序列值之間不存在任何的相關性,那就表明該序列是一個無記憶的序列,過去的行為對未來的走勢沒有任何影響,這種序列稱為純隨機性序列。序列的純隨機性檢驗,我們可以采用假設檢驗的方法。由于序列的相關性具有偶然性,則原假設:延遲期數小于或等于m期的序列值,且相互獨立,即如下表述:
(1)假設條件
H0:p1=p2=…pm=0,m≥1;
H1:至少存在某個pk≠0,m≥1,k≤m
(2)檢驗統計量LB
根據LB統計量,它服從自由度為m的卡方分布(m為指定延遲階數)。
檢驗結果顯示,在6階延遲下LB統計量的 p值為0.0076,遠小于a(a=0.05)。又因為平穩序列通常具有短期相關性,所以有很大把握拒絕原假設,此序列為非白噪聲序列。
4.擬合ARIMA(p,d,q)模型
模型根據平穩時間序列的自相關階數 p和移動平均階數q的截尾性和拖尾性,選擇適當的值來進行擬合。根據樣本自相關圖顯示,除了延遲一階的自相關系數在2倍的標準差范圍之外,其他階數的自相關系數都在2倍標準差之內波動,可以認為該序列自相關系數一階截尾,可以用ARIMA(0,1,1)擬合模型。根據樣本的偏自相關圖顯示,除了延遲一階的偏自相關系數在2倍標準差范圍之外,其他階數的自相關系數都在2倍標準差之內波動,可以認為該序列自相關系數一階截尾,可以用ARIMA(1,1,0)擬合模型。綜合樣本的自相關圖與偏自相關圖,也可以選擇ARIMA(1,1,1)。
5.參數估計與模型檢驗
對擬合好的模型進行參數估計,通常有三種方法(矩估計、極大似然估計、最小二乘估計),這里采用最小二乘估計法。在ARMA(p,q)模型場合下,計算殘差平方和達到最小的那組參數是模型參數估計值。再對估計的參數進行顯著性檢驗,檢驗參數所對應的自變量對因變量的影響是否明顯。
(1)若p=1,擬合ARIMA(1,1,0)
參數的估計值Φ1=0.74260,檢驗未知參數顯著性的t檢驗統計量p 〈0.0001,說明該參數顯著非零。
(2)若q=1,擬合ARIMA(0,1,1)
參數的估計值θ1=0.75855,檢驗未知參數顯著性的t檢驗統計量p 〈0.0001,說明該參數顯著非零。
(3)若p=1,q=1,擬合ARIMA(1,1,1)
參數的估計值Φ1=0.61954,θ1=-0.27081,θ1的檢驗0.3091明顯大于0.05,所以參數檢驗不顯著,模型需舍棄。
6.模型的顯著性檢驗
如果模型擬合的殘差項中不再含有任何相關信息,即殘差序列為白噪聲序列,這樣的模型稱為顯著有效模型。與此同時,構建LB統計量,原假設殘差序列為白噪聲序列,然后對LB統計量進行白噪聲檢驗。從檢驗的結果能夠得到模型LB統計量的p值均明顯大于0.05,所以兩個模型均顯著有效。
7.模型的最優選擇
模型的選擇是預測工作的重要環節,實證研究表明,同一個序列不僅僅只能構造一個擬合模型,那么選擇哪個模型用于統計推斷呢?
為了解決這個問題,需引進SBC和AIC信息準則的概念。AIC認為一個擬合模型的好壞可從以下兩方面去考慮:一方面是擬合程度的似然函數值,另一方面是模型中未知參數的個數。似然函數值越大,說明擬合的效果越好;模型未知參數個數越多,說明模型中包含的自變量越多,模型擬合的準確度就越高,但單純的以比擬合精度來衡量模型的好壞,肯定會導致未知參數越來越多,自變量以及未知參數的增多就會導致較多的未知的風險。這樣一來不僅增加了工作難度,而且估計的精度也會越來越差,所以一個好的擬合模型應該是擬合精度和未知參數個數的綜合最優配置。
就一個觀察序列而言,序列越長,相關信息就越分散,而且有時候時間序列的相關性衰減,會導致其只適合短息預測。那么要很充分地提取其中的有用信息,通常就需要多自變量復雜模型。以下分別是AIC和SBC準則:
AIC=-2In(模型的極大似然函數值)+2(模型中的未知參數的個數)
中心化的ARMA模型的AIC函數為:
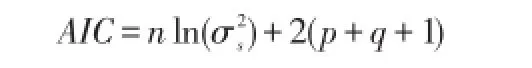
非中心化的為:

中心化的:

非中心化的:
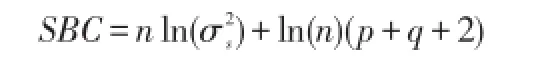
通過比較可以發現,在AIC準則中擬合誤差提供的信息要受到樣本容量的放大,但參數個數的懲罰因子卻和樣本沒有關系,它的權重始終是常數2,在樣本容量趨于無窮大時,它比真實模型所含的未知參數個數要多。SBC將懲罰權重改為樣本容量的對數函數,理論上已經證明SBC準則是最優模型的真實階數的相合估計。
在盡可能全面的范圍里考察有限多個模型的AIC和SBC函數值,得出SBC模型是一個相對最優模型。SBC準則的提出,可以有效地彌補根據自相關圖和偏自相關圖定階的主觀性,在有限的階數范圍內,找到最優擬合模型。因為在自然科學內,規律確實是存在的,且關系是精確的,在相當長的時間內,這些規律關系會保持不變,但在經濟領域內則完全是另一回事,經濟模式或關系往往與隨機噪音交織在一起,改變經濟現象的可預測性的因素太多,比如,人類行為的變化無常,某種重大事件的發生等等都會對經濟現象有所影響,所以在很多時候,分析數據都依靠分析人員的經驗,主觀因素非常大,而SBC恰好彌補了這一點,所以說對模型地優化和選擇幫助非常大。
檢驗結果如表所示,檢驗表明,ARIMA(1,1,0)比ARIMA(0,1,1)相對更優。
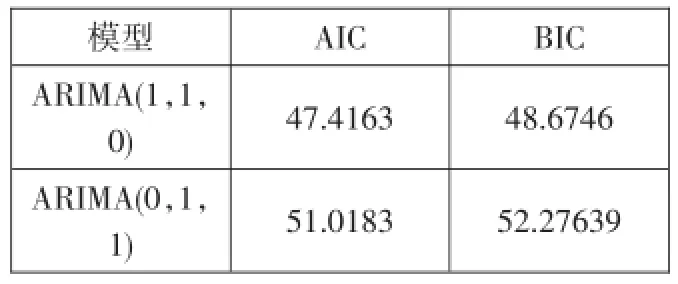
模型ARIMA(1,1,0)ARIMA(0,1,1)AIC 47.4163 BIC 48.6746 51.0183 52.27639
五、模型預測與決策
通過對模型的檢驗,得到最優模型方程為:1.7426Xt-1-0.7426Xt-2+e=Xt。對模型進行預測得出:最新發布的數據。對比可以得出,8月份的預測精確到了小數點后兩位,這一點說明模型相對來說還是比較合適的;9、10月份的預測值則表現出了較大地不一致性,絕對誤差表現的很大,但通過相對誤差地比較,得出數據仍然在95%的置信區間,說明擬合還是有效的。
根據定性分析和定量分析,可以認識到PPI的下降還將持續,這意味著我國的需求萎縮的狀況依然存在。因此,中國工業領域必然會經歷一個去產能化的過程,也就是淘汰過剩的產能。所以當PPI下降的時候,不能過度解讀為實體經濟的收縮,應稱之為一次中國工業領域的刮骨療傷。當前中國工業的過剩產能需要通過低價格來進行市場壓縮,否則很難通過行政手段干預。因此,需要提高對經濟下行,PPI下降的承受力,從而推動對中國工業產能的控制、產業升級以及結構優化。
六、總結
1.模型的缺陷
ARIMA模型需要歷史數據,一般要求不少于50個,然而實際情況是不一定能得到如此多的數據,但是預測還是呈現出越來越準確的趨勢。在ARIMA模型中,序列變量的未來值被假定滿足變量過去觀察值和隨機誤差值的線性函數關系,可是現實中絕大多數的時間序列都包含非線性關系。
2.遇到的困難
經濟指數很容易受各種影響,如果選取的時序樣本較長,且波動比較大的時候,很難建立ARIMA模型;同比指數能消除季節性的因素,相比環比數據,建立ARIMA模型更簡單;運用較長、波動大的數據時,建立ARIMA的殘差序列很難實現非白噪聲序列,通常是由于模型對數據信息提取不充分;價格指數不可能永遠上漲,它必然是上下浮動的,所以很難進行長期預測。
參考文獻
[1]薛冬梅.ARIMA模型及其在時間序列分析中的應用[J].吉林化工學院學報,2010-6(27).
[2]王燕.應用時間序列分析[M].北京:中國人民大學出版社,2005:41-152.
[3]易丹輝.數據分析與Eviews應用[M].北京:中國統計出版社,2003:106-132.
[4]劉薇.時間序列分析在吉林省GDP預測中的應用[M].長春:東北師范大學,2008.
[5]田錚譯.時間序列分析的理論與應用[M].北京:高等教育出版社,2003:214-246.
(作者單位:上海理工大學管理學院)
DOI:10.16653/j.cnki.32-1034/f.2016.10.043

