經編網眼織物設計的數學描述

張靈婕，繆旭紅

(江南大學 教育部針織技術工程研究中心，江蘇 無錫 214122)

經編網眼織物設計的數學描述

張靈婕，繆旭紅

(江南大學 教育部針織技術工程研究中心，江蘇 無錫 214122)

經編網眼織物設計的研究都只是進行規律性概括，缺乏從數學角度進行描述。為此，對變化經平類網眼織物進行分類，并針對不同變化經平類網眼織物的設計方法進行探討，建立了經編網眼織物穿經循環縱行數、組織循環橫列數與墊紗組織、最大墊紗數碼及基礎組織針數等參數的數學關系，并在已知穿經循環針數、組織循環針數、移針針數等條件下，通過簡單計算判斷網眼織物分布類型以及網眼位置，為該類網眼織物設計提供理論參考，有效提高設計效率。

經編網眼；設計；數學計算；網孔位置

經編擅長形成形狀和大小各異的網眼織物，織物具有網眼大小可控、無結頭、表面光滑、耐磨損、質輕、形狀穩定等優點[1]，因此經編網眼織物應用領域廣泛，已在服裝、裝飾、家居[2]等眾多行業得到應用,并且在產業領域如醫學[3]、建筑、航空航天[4]等中的應用越來越多。基于對網眼織物的需求越來越大，掌握網眼織物的設計技巧及方法可更加快速高效地設計出所需的網眼產品。

網眼形成具有一定的規律，近些年來研究人員主要對網眼織物的設計方法[5-6]、分析方法、織物性能、特點[7]、工藝參數與力學性能的關系[8]以及應用等方面取得了階段性成果，由于計算機技術的發展，國內外相關人員也開始了對經編織物仿真技術的研究，預測產品的外觀以及性能[9]，使得織物設計更好地適應數字化時代。雖然以上文獻作出了一些結論，但并未能采用數學的方式描述網眼織物墊紗組織、穿經和網眼位置的關系。本文通過對以經平為基礎組織采用空穿形成的一類網眼進行歸納總結，揭示空穿型網眼織物組織、穿經和網孔分布之間的關系，總結網眼形成規律，為網眼織物的設計提供參考，并為網眼織物的開發提供思路。

1 網眼形成原理及方法

經編織物中當相鄰2個線圈縱行在局部失去聯系，即無紗線連接2個線圈縱行時，就可形成網眼[10]。經編擅長形成各類網眼，形成經編網眼織物的方法也多種多樣，常用來形成網眼的有少梳櫛技術、多梳櫛技術、雙針床技術及賈卡技術[11]。少梳櫛技術根據形成網眼的組織類型，基本上可分為3類：以經平、經緞組織為基礎組織變化加上空穿形成網眼；運用編鏈和襯緯組織為基礎變化形成網眼；運用缺墊組織形成網眼。

第1類網眼形成的網孔一般為形狀對稱的橢圓形、菱形或六角形，應用廣泛，性能優異，根據梳櫛的墊紗配合可分為對稱墊紗網眼和非對稱墊紗網眼。兩把梳對稱墊紗形成網眼是最為常見的設計，且兩把對稱墊紗的導紗梳通常采用上下對稱的墊紗組織，以使組織結構均勻穩定。此類網眼織物設計規律顯著，本文將針對此類網眼織物形成方法進行探討。

根據網孔分布的情況，經編網眼織物可分為直線分布、交錯分布以及復合分布網眼織物。網孔在織物上成橫縱直線排列的二方連續分布稱為直線分布，而網孔在織物上成四方連續排列的分布稱為交錯分布。復合型分布是直線型和交錯型的組合和變化，分布規律更復雜，變化也更多。網眼分布類型如圖1所示。

圖1 網眼分布類型Fig.1 Mesh distribution type.(a) Linear mesh; (b) Cross mesh; (c) Composite mesh

2 經編網眼織物的形成規律

2.1 織物結構參數

對于以經平為基本組織的網眼(經緞組織可看成是經平組織的特例)，在織物上可分為基礎組織區域和變化組織區域，基礎組織一般使用2橫列及以上的2至4針經平組織，變化組織區采用變化經平、經緞、變化經緞等組織。在此，先探討一個穿經循環僅形成一個網孔的直線分布以及交錯分布的網眼織物。設：RC為墊紗組織循環橫列數；RW為穿經循環縱行數；TI為連續穿經數，TO為連續空穿數，Lmax為墊紗組織最大數碼(最大累積橫移)；基礎經平組織的針數為BS；基礎組織的橫列數為RCB(經緞組織RCB=2)；變化組織區域橫列數為RCM；變化區域橫列移針總數為ST；變化區域平均每橫列移針數為SA。如圖2所示。

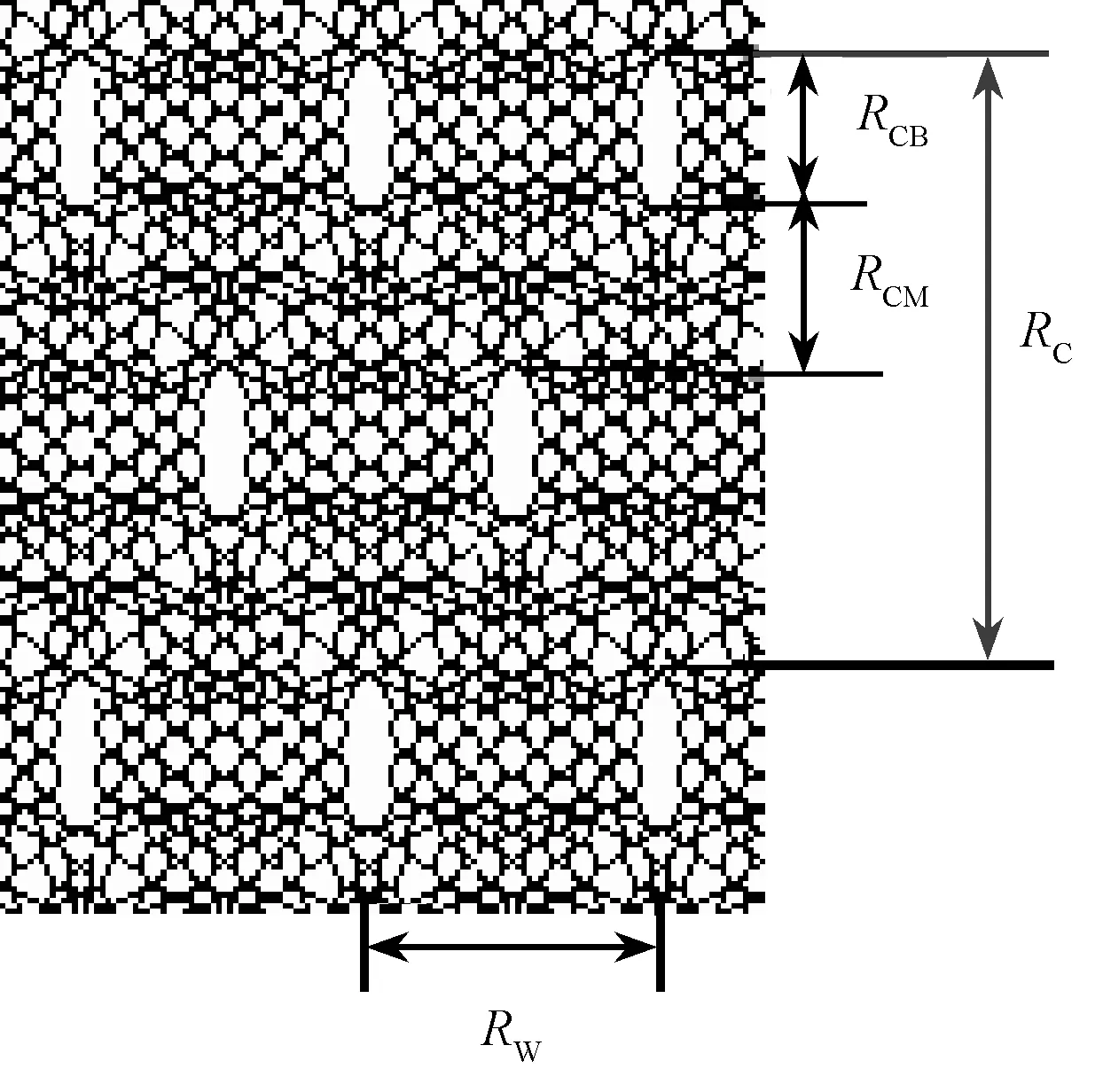
圖2 織物結構參數Fig.2 Parameters of fabric structure

則有：

(1)

(2)

(3)

2.2 網眼織物形成條件

能否形成網孔并能保證每根織針上至少能墊入1根紗線成圈[12]，織物結構參數必須滿足以下幾個條件。

1) 每個穿經循環中空穿數至少為1，最大不超過BS-1。

2) 連續空穿數TO要小于連續穿紗數TI。

3) 在基礎組織區域，前后梳櫛導紗針至少在1個織針間隙均空穿，在此位置上形成網孔。

4) 穿經循環縱行數RW和組織循環橫列數RC均為偶數。

5) 如在1個穿經循環中僅形成1個網孔，且在基礎組織處對紗，正常網孔形成的穿紗和對紗規律如下：

(4)

(5)

右起經平，穿TI,空BS-1

左起經平，空BS-2,穿TI,空1

右起經平指導紗梳起始橫列在第1根針上墊紗，延展線從右向左；左起經平指導紗梳起始橫列在最后1根針上墊紗，延展線從左向右。

2.3 最大墊紗數碼

形成直線型或交錯型網眼的最大墊紗數碼Lmax、橫移總針數ST與穿經循環根數RW之間存在以下關系。

1) 直線型。

ST=xRW

(6)

(7)

式中x=1,2，為在最少移針針數內實現所有墊紗情況，一般x取1。

2) 交錯型。

ST=xRW+RW/2

(8)

(9)

式中x可取0，1，2，…，同樣為在最少移針針數內實現所有墊紗情況，一般x取0。

直線型網眼可看成是交錯型網眼的特例，即在交錯型網眼的中間可形成網眼位置設計為變化組織區域，這樣在該處不會形成網眼，即形成了直線型網眼。

3 網眼織物設計

3.1 常規網眼設計

3.1.1 直線型網眼設計

根據上文所述網眼織物形成條件以及各織物參數關系進行直線型網眼織物設計。現設計1個穿經循環為6縱行，基礎組織采用2針經平，組織循環為12橫列，網眼區域橫列數m=3的直線型分布網眼織物。

則據式(4)可知連續穿紗數為

據式(5)可知連續空穿數為

則穿經對紗為：GB1(右起經平)，穿5空1；GB2(左起經平)，穿5空1。

GB1表示經編機第1把梳櫛；GB2表示經編機第2把梳櫛。

據式(2)知：RCM=RC/2-RCB=3，即變化組織橫列數RCM為3。

據式(6)得，變化組織區域移針總數ST=6。

據式(3)得，變化組織區域平均移針數SA=ST/3=2。

據式(7)得最大墊紗數碼Lmax=RW+BS=8。

墊紗組織設計如下。

墊紗組織：

GB1，1-0/ 1-2/ 1-0/ 1-2/ 3-4/ 5-6/ 7-8/ 7-6/ 7-8/ 6-5/ 4-3/ 2-1//

GB2，7-8/ 7-6/ 7-8/ 7-6/ 5-4/ 3-2/ 1-0/ 1-2/ 1-0/ 2-3/ 4-5/ 6-7//

穿經：GB1，5穿1空；GB2，5穿1空。

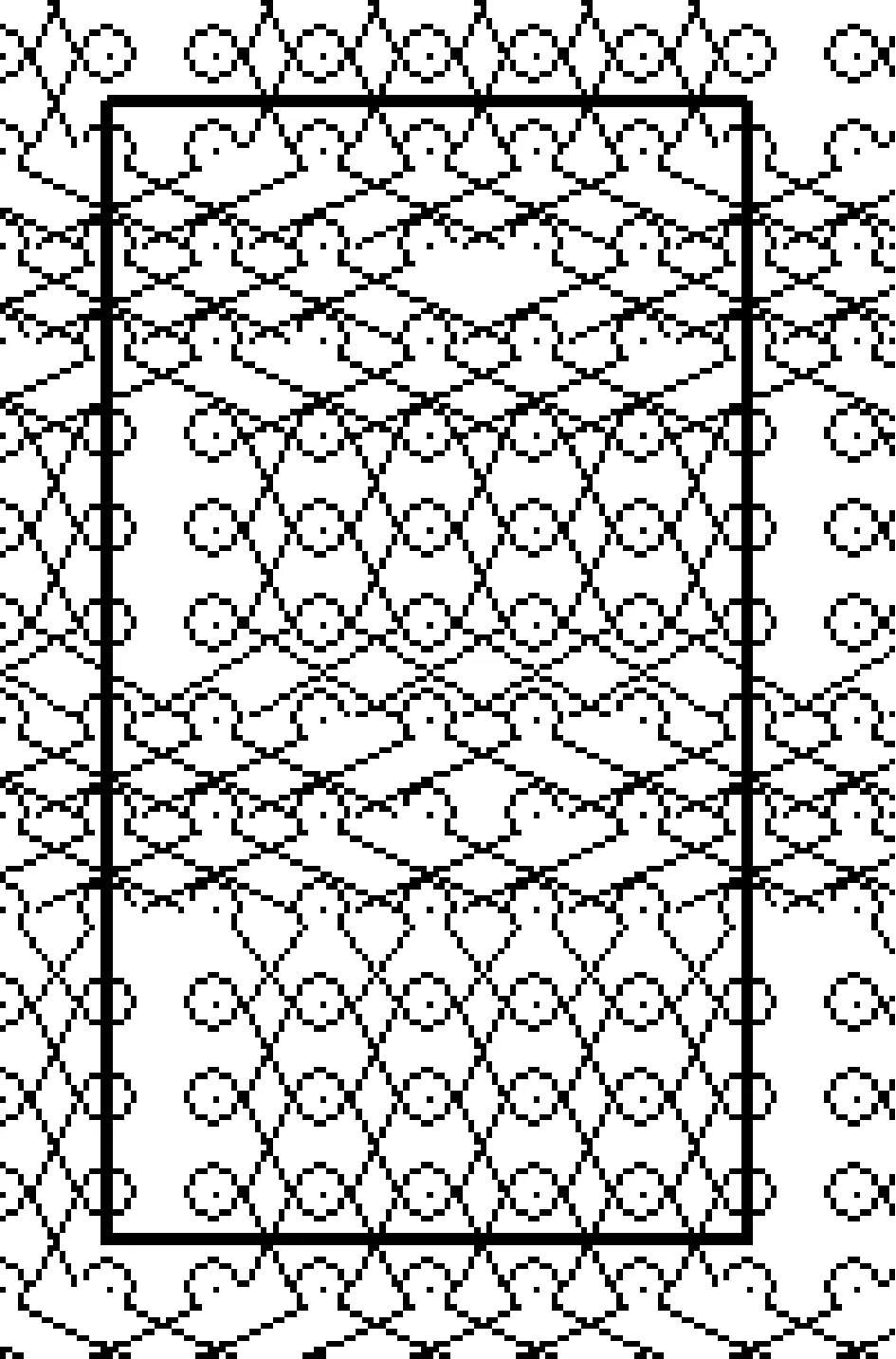
圖3 直線型網眼織物墊紗運動圖Fig.3 Linear mesh fabric lapping diagrams

該直線型網眼織物墊紗運動圖如圖3所示。連接區域可考慮使用經平或者經緞組織。經平組織因為進行移針時“一進一退”，需要更多的橫列數完成要求的橫移針數。經緞組織因為一直進行單方向的移針動作，所以當橫移針數較大，變化組織橫列數RCM較少時，一般選用經緞組織完成。

3.1.2 交錯型網眼設計

同樣采用2針經平作為基礎組織，組織循環為12橫列，網眼區域橫列數RCB=3來設計一款交錯型分布網眼織物。上面實例中的組織橫移總針數ST為6，若采用同一組織，據式(8)可知，只需改變穿經循環為RW=ST×2=12即可。則：

據式(4)連續穿紗數為TI=RW-BS+1=11。

據式(5)連續空穿數TO=BS-1=1。

則穿經對紗為：GB1(右起經平)，穿11空1；GB2(左起經平)，穿11空1。

根據式(2)得：

RCM=RC/2-RCB=3，即變化組織橫列數RCM為3。

根據式(8)得變化組織區域移針總數ST=RW/2=6。

據式(3)得得變化組織區域平均移針數SA=ST/3=2。

據式(9)得最大墊紗數碼Lmax=xRW+RW/2+BS=8。

墊紗組織設計如下。

GB1: 1-0/ 1-2/ 1-0/ 1-2/ 3-4/ 5-6/ 7-8/ 7-6/ 7-8/ 6-5/ 4-3/ 2-1//

GB2: 7-8/ 7-6/ 7-8/ 7-6/ 5-4/ 3-2/ 1-0/ 1-2/ 1-0/ 2-3/ 4-5/ 6-7//

穿經設計：GB1，11穿1空；GB2，11穿1空。

該交錯型網眼織物墊紗運動圖見圖4。

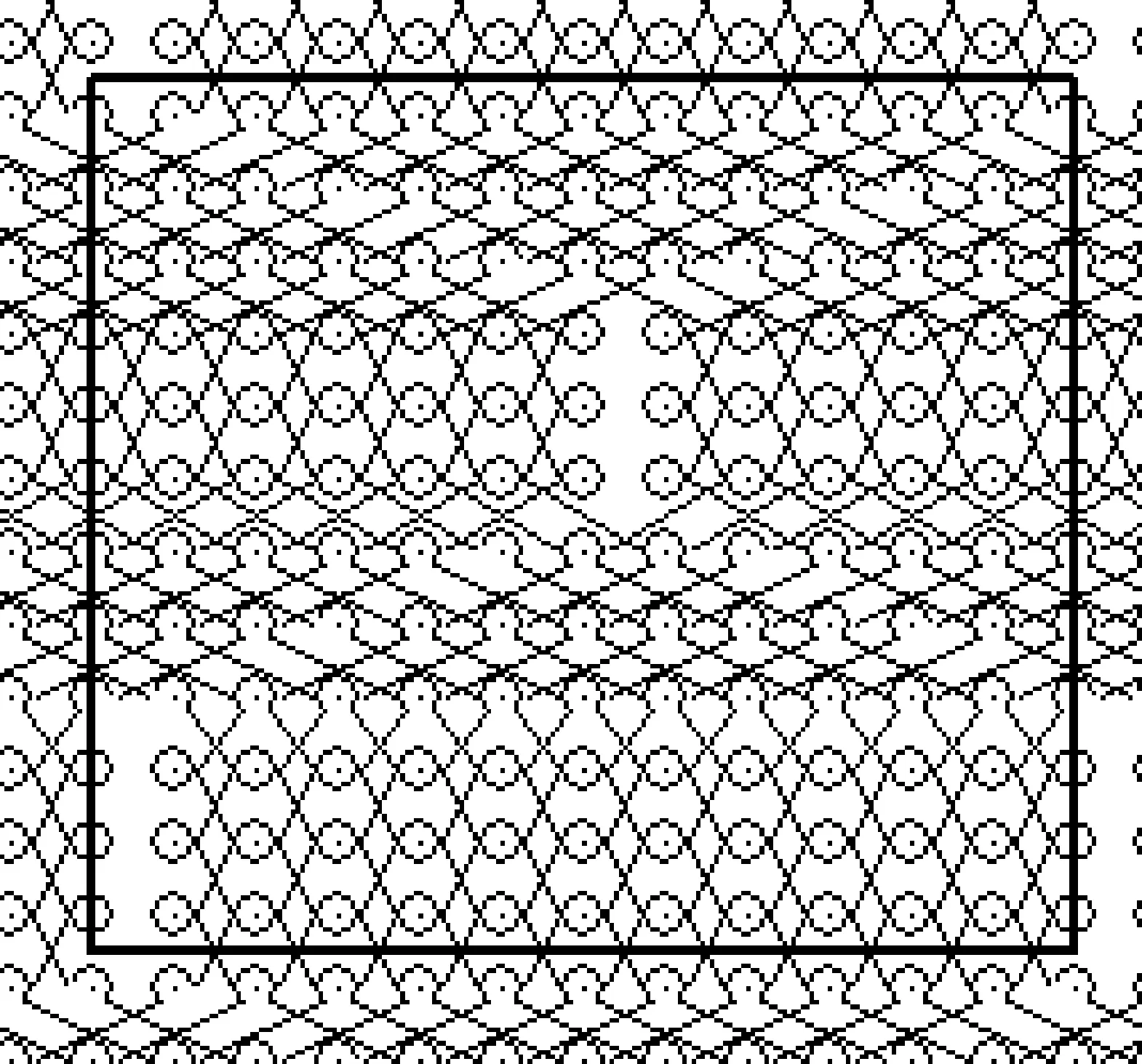
圖4 交錯型網眼織物墊紗運動圖Fig.4 Staggered mesh fabric lapping diagrams

3.2 復合網眼織物的設計

當一個穿經循環內不止一處空穿時，依靠兩梳對稱橫移墊紗可形成復合交錯的較復雜的網孔分布。連續空穿數大于1的復合網眼織物設計較復雜，較少使用。因此，采用兩針經平作為基礎組織來討論復合網眼織物的設計。

3.2.1 穿經規律數學描述

進行復合網眼織物設計首先要先確定穿經。根據1個穿經循環內網眼的個數以及位置來確定空穿根數和位置，即在需形成網眼位置兩把梳同時空穿；根據網眼間隔大小確定連續穿經根數。

假設穿經循環RW內共空穿n針，n≥ 1，則2把梳穿經均為I1穿，1空，I2穿，1空，……，Im穿,1空，……，In穿，1空。

(10)

當n=1時形成常規網眼織物。In一定為奇數，不僅可避免橫移過程中的漏針情況，而且可使網孔分布情況更加豐富。

使用二維矩陣T表示起始穿紗規律[13]，

tij表示矩陣內元素，數值等于1或0，0表示空穿，1表示穿紗；t1j表示GB1的起始穿經狀態，t2j表示GB2的起始穿經狀態。

根據上述穿紗規律可知：

(11)

穿經確定后可進行其他織物參數計算：

(12)

ST=RW/2

(13)

3.2.2 網孔形成位置計算

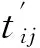
假設GB1采用右起經平，GB2采用左起經平，x表示2把梳相對于起始墊紗位置橫移的針數，x≤ST，GB1向左移x針，GB2向右移x針。

(14)

(15)

(16)

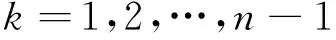
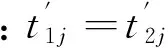
(17)

(18)

織物在初始位置和2把梳橫移RW/2針時，可形成的網孔數最多，為n個網孔，其他處形成的網孔數在1到n-1之間。

3.2.3 設計實例

設計一個1穿1空，1穿1空，3穿1空的復合交錯網眼：n=3，表示穿經循環RW=2+2+4=8針內空穿3針；據式(12)、(13)知ST=4，Lmax=6。

據式(11)可知j=2、4、8時，t1j=t2j=0。

綜合式(14)～(17)求出符合要求的x、j值，計算結果如下：

x=1時，在第1、2和第3、4根針間形成網眼；

x=2時，在第2、3和第6、7根針間形成網眼；

x=3時，在第5、6和第7、8根針間形成網眼；

x=4時，在第4、5，6、7和8、9根針間形成網眼。

圖5示出2+2+4復合網眼墊紗圖，圖6示出2+2+4復合網眼仿真圖。

圖5 2+2+4復合網眼墊紗圖Fig.5 2+2+4 recombination mesh lapping diagrams

圖6 2+2+4復合網眼仿真圖Fig.6 2+2+4 recombination mesh simulation diagram

根據實際墊紗圖判斷計算結果正確，證明可使用該方法判斷復合交錯網眼分布情況。

4 結 論

1)對稱型經編網眼織物具有很強的設計規律，常規的網眼織物穿經循環縱行數、組織循環橫列數與墊紗組織、最大墊紗數碼及基礎組織針數等織物參數之間存在明確的數學關系，在已知組織循環橫列數和穿經循環縱行數的情況下，可設計出相應的網眼墊紗組織和穿經。

2)在總結常規網眼織物網眼設計規律和方法的基礎上，對復合網眼織物網眼形成規律研究的結果表明，在已知基礎組織、穿紗情況、移針針數情況下，通過簡單的計算可判斷網眼分布類型以及網眼的位置。

3)對常規網眼織物及復合網眼織物各織物參數建立了數學關系，可有效提高該類網眼織物的設計效率，為該類網眼織物設計提供理論參考。

FZXB

[1] 蔣高明.現代經編工藝與設備[M].北京: 中國紡織出版社,2001:1-3.JIANG Gaoming.Modern Warp Knitting Technology and Equipment [M].Beijing: China Textile & Apparel Press,2001:1-3.

[2] 叢洪蓮,李秀麗.經編產業用紡織品的生產與開發[J].紡織導報,2011(7):29-33.CONG Honglian ,LI Xiuli.The production and the development of the warp knitting industrial textiles [J].China Textile Leader,2011(7): 29-33.

[3] AKOLEKAR D ,KUMAR S ,KHAN L R ,et al.Comparison of recurrence with light composite polypropylene mesh and heavy weight mesh in laparoscopic totally extraperitoneal inguinal hernia repair: an audit of repairs [J].Hernia,2008,12(1):39-43.

[4] 陳南梁.經編網眼織物在高科技紡織品中的應用[J].紡織導報,2013(9):68-70.CHEN Nanliang.Warp knitted mesh fabric in the application of high tech textiles [J].China Textile Leader,2013(9):68-70.

[5] WE L,XUN Weifeng.Analysis and design of warp knitting net fabrics[J].Journal of China Textile University(English Edition),1998(1):70 - 72.

[6] 陳莉,葉介茂.基于數學函數的針織物花型設計方法初探[J].紡織學報,2008，29(7):38-40.CHEN Li,YE Jiemao.Knitted fabric pattern design method based on mathematical function study [J].Journal of Textile Research,2008,29(7): 38-40.

[7] 毛一新.經編織物的組織結構分析淺見[J].針織工業,1990(5):23-26,39.MAO Yixin.Warp knitted fabric structure analysis imho [J].Knitting Industries,1990,5):23-26,39.

[8] 劉曉明，陳南梁，馮勛偉.經編網格織物工藝參數對強力的影響[J].針織工業，2007(6):20-22.LIU Xiaoming,CHEN Nanliang,FENG Xunwei.The influence of process parameters on the warp knitted mesh fabric strength [J].Knitting Industries,2007 (6): 20-22.

[9] ZHANG L Z,JANG G M,GAO W D.3D Simulation of two-bar warp-knitted structures[J].Journal of Donghua University (English Edition),2009(4):423-428.

[10] 張佩華，沈為.針織產品設計[M]北京:中國紡織出版社,1998:15-20.ZHANG Peihua,SHEN Wei.Knitting Product Design [M].Beijing: China Textile & Apparel Press,1998:15-20.

[11] 趙西娜,鄧中民.經編網眼運動鞋幫面面料的數字化設計與仿真[J].針織工業,2014(4):16-18.ZHAO Xina,DENG Zhongmin.Warp knitting mesh motion upper surface fabric of digital design and simulation [J].Knitting Industries,2014(4):16 -18.

[12] 邱璟,張蘋,胡卜文,等.雙梳對稱網眼織物的分析與設計方法[J].針織工業,2010(12):7-10.QIU Jing,ZHANG Ping,HU Buwen,et al.Analysis and design method of double comb symmetrical mesh fabric [J].Knitting Industries,2010(12) : 7-10.

[13] CHEN Li,ZHANG Rui,YE Jiemao.Study on how to design knitted fabric pattern with mathematical theory [J].Journal of Donghua University(English Edition),2009(2):204-206.

Mathematical description on warp knitted mesh fabric design

ZHANG Lingjie,MIAO Xuhong

(EngineeringResearchCenterofKnittingTechnology,MinistryofEducation,JiangnanUniversity,Wuxi,Jiangsu214122,China)

The research on warp-knitting design is focused on the regular summary,which is in shortage of the mathematical description.In this paper,the category of tricot stitch mesh fabric is classified and the design method of different kinds of tricot stitch mesh fabric is discussed.The mathematical relationship of design parameters such as drawing-in cycle count,structure cycle of horizontal longitudinal and mat yarn group,the largest yarn mesh code and the needle number of basic structure are studied.Based on the previous study,the distribution type of mesh fabric and the mesh position can be calculated according to the drawing-in cycle needle number,structure cycle needle number and the moved needle number.The present study can provide the theoretical basis for this kind of mesh fabric,and can improve the design efficiency of this mesh fabric as well.

warp knitting mesh; design; mathematical calculation; mesh position

10.13475/j.fzxb.20141205406

2014-12-26

2015-05-23

中央高校基本科研業務費重點項目(JUSRP51404A);江蘇省產學研項目(BY2014023-34)

張靈婕(1992—)，女，碩士生。研究方向為紡織材料與紡織品設計。繆旭紅，通信作者，E-mail: miaoxuhong@163.com。

TS 184

A