運用離散事件仿真的羅拉牽伸模型

麻寶龍，汪 軍,2

(1.東華大學 紡織學院，上海 201620；2.東華大學 紡織面料技術教育部重點實驗室，上海 201620)

運用離散事件仿真的羅拉牽伸模型

麻寶龍1，汪 軍1,2

(1.東華大學 紡織學院，上海 201620；2.東華大學 紡織面料技術教育部重點實驗室，上海 201620)

為研究羅拉牽伸過程中纖維的運動規律和預測牽伸后輸出條干的質量，在離散系統建模技術的基礎上，提出利用離散事件仿真羅拉牽伸過程的方法。將紡織牽伸理論與離散理論相結合建立了羅拉牽伸離散事件仿真模型，并討論模型中參數變化對輸出條干不勻的影響。結果表明：該模型能夠體現出羅拉牽伸過程中須條運動的動態特性，仿真中可通過追蹤每根纖維經過牽伸區的運動過程。通過與實際試驗數據的比對，證明該模型能夠預測出牽伸后輸出須條的條干不勻規律。通過對所建模型中各輸入參數的討論指出，纖維長度和輸入須條線密度是羅拉牽伸過程中最重要的影響因素。

羅拉牽伸；條干不勻；離散事件系統；仿真模型

羅拉牽伸是紡紗過程中的重要環節，條干不勻率是評價牽伸效果的重要指標之一。如何通過完善牽伸理論，優化羅拉牽伸配置，降低牽伸過程中附加條干不勻，是紡織研究領域的基礎性問題之一。關于牽伸不勻的本質方面討論：Martindale[1]首先在假設纖維等長的基礎上提出了紗線極限不勻公式；Rao[2]在其基礎上證明了纖維的頭端分布符合泊松分布，并推導出其不勻率公式；其他學者也討論了纖維長度、線密度等材料屬性以及牽伸倍數、羅拉隔距等工藝參數對條干不勻率的影響[3-6]，得出具有規律性的結論。但是這些討論并不能說明須條輸出的動態特征，所以通過數學建模方法仿真羅拉牽伸過程是研究條干不勻的另一個重要方面。從牽伸模型的建立方面，很多學者采取了線性控制方式來優化牽伸過程[7-9]；Johnson[10]也在假設隨機須條及纖維頭端分布的基礎上仿真了牽伸過程，給出了牽伸不勻的相關圖；Djiev[11]依據質量守恒建立了一個牽伸模型，之后Huang[12]應用最小方差控制對該模型進行了優化；Huh等[13-15]根據質量和動量守恒建立了纖維束牽伸運動模型，并模擬了紗條的動態運動特征；Cherkassky[16-17]利用離散事件仿真也建立了一個羅拉牽伸模型，但其采用距離等效運動時間的方法并不能真正反映羅拉牽伸過程中纖維的運動規律。有研究者指出模型能夠給出牽伸過程中的某些規律，但是這些假設模型卻較少關注實際羅拉牽伸過程中的參數設置，故模型的仿真結果也只能用于討論牽伸過程中的某些性質[18-19]。

離散事件系統是指受隨機離散事件驅動、系統狀態呈跳躍變化的動態系統，其核心為安排和處理離散事件[20]。該仿真方法的主要目標是獲得系統行為的統計性能，而不是狀態變量的動態變化過程。離散事件系統本身就是一個存在各種隨機因素的仿真系統，而紡紗過程中的牽伸就是典型的隨機過程。本文將單根纖維看作離散事件系統中的一個活動實體，利用活動實體在離散事件系統中從產生到消亡的過程來模擬單根纖維在牽伸區內的運動過程，建立羅拉牽伸模型；然后通過統計纖維在牽伸區內每個截面處的根數變化來討論羅拉牽伸過程，驗證模型的正確性并指出影響條干不勻的主要因素。

1 模型的建立

1.1 仿真原理

在離散事件仿真過程中每個活動實體都是系統的處理對象，離散隨機事件用于改變活動實體的狀態并推動仿真的進程。在羅拉牽伸模型中每個活動實體從產生到消亡的過程，即為每根纖維從進入牽伸區到移出牽伸區的運動過程；離散事件發生的時刻即為每根纖維運動狀態發生改變的時刻，羅拉牽伸模型的系統狀態也在這些時刻點發生變化。按照離散隨機事件的發生順序，逐個處理離散事件并推動仿真進程，以此來模擬羅拉牽伸中每根纖維通過牽伸區并發生速度改變的過程。羅拉牽伸模型仿真過程中未消亡的活動實體數量即為此時存在于牽伸區內的纖維數量。

為方便對羅拉牽伸過程的討論，也能夠使所建立的羅拉牽伸模型符合離散事件仿真的特性，需要對該羅拉牽伸模型建立的前提條件作出如下假設：

1)每根纖維均伸直平行，且只沿須條長度方向運動；

2)纖維在牽伸區內的運動過程為獨立隨機離散事件；

3)纖維在變速點處瞬間變速，即每根只有后羅拉速度和前羅拉速度2種運動速度。

根據離散事件仿真系統的特點，建立該羅拉牽伸模型的思路如下。

1)辨識系統的實體及屬性。將一根纖維看作離散事件系統里的一個活動實體，其屬性根據纖維的類型不同而定，如纖維長度、線密度等。各個活動實體之間的屬性差異即為須條中每根纖維的性質差異，如纖維長度滿足某種分布等。

2)分析每個實體的狀態。活動實體在離散事件仿真過程中保持的狀態，該羅拉牽伸模型每根纖維只有慢速運動和快速運動2種狀態。

3)確定系統事件和活動。將每根纖維通過牽伸區分為幾個過程，即每個活動實體從產生到消亡要經過幾個事件，每兩個事件之間保持某一狀態的持續時間長短。

4)分析每次事件發生時，模型系統狀態的變化情況。

5)給出羅拉牽伸模型各參數的取值、參變量的計算方法以及屬性描述變量的取值方法。

在上述假設的基礎上，研究單根纖維經過羅拉牽伸的過程如圖1所示。

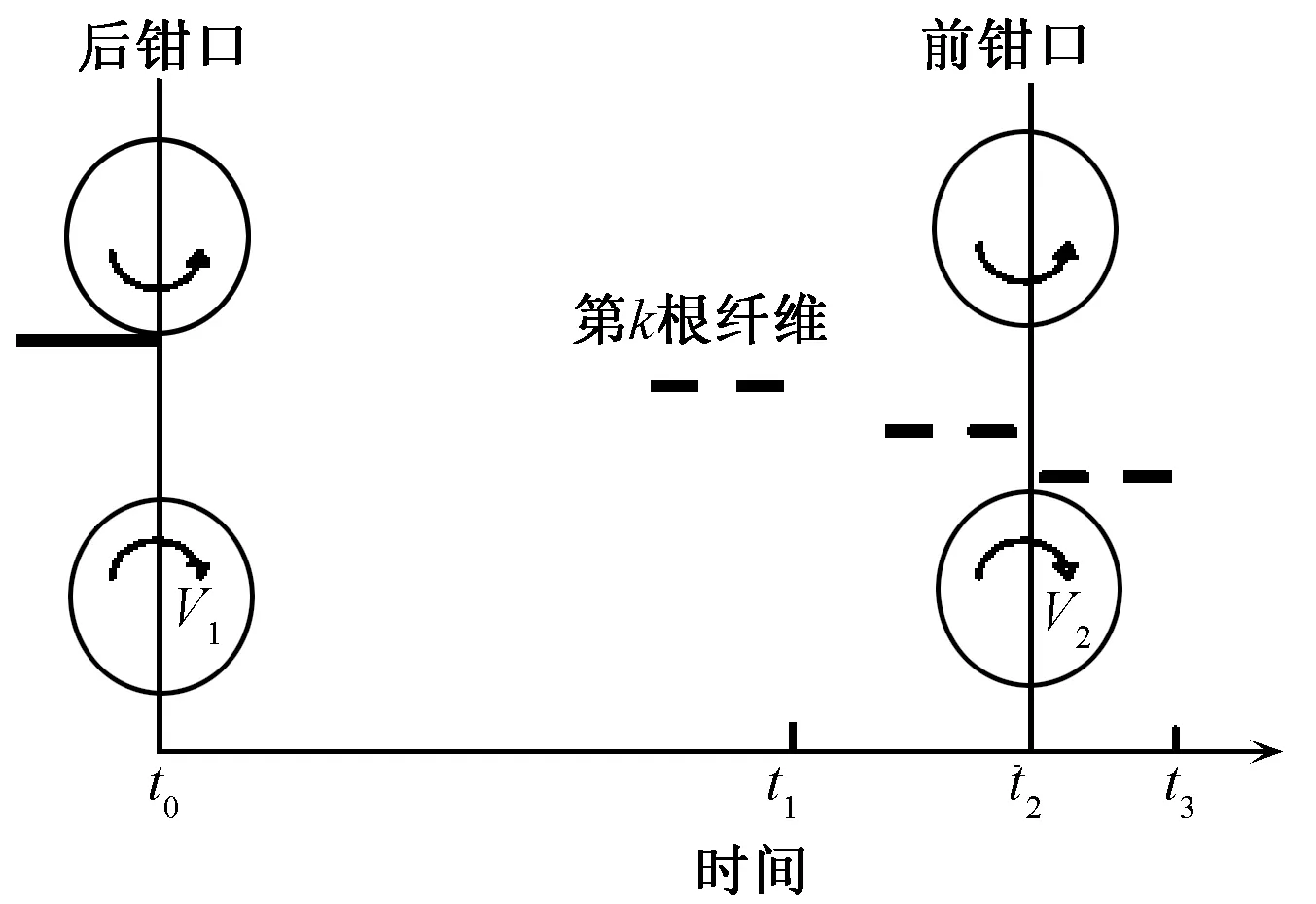
圖1 單根纖維經過羅拉牽伸過程示意圖Fig.1 Schematic drawing of a single fiber in drafting zone

以第k根纖維經過牽伸區的過程為例，橫坐標軸代表第k根纖維將要在牽伸區內發生狀態改變的時刻，即離散事件發生的時刻點。從圖中可看出，該羅拉牽伸模型將每根纖維通過牽伸區的過程劃分為4個階段，即每個活動實體從產生到消亡的過程中會在4個時刻點發生離散事件。

1)纖維頭端進入牽伸區。羅拉牽伸模型在t0時刻產生一個活動實體，表示第k根纖維在t0時刻到達后羅拉鉗口處，該活動實體的屬性為須條中第k根纖維的屬性。該纖維以后羅拉速度進入牽伸區，屬于后纖維，即在整根纖維通過后羅拉的過程中完全受后羅拉的強控制，不會產生變速。

2)纖維在牽伸區內變速。羅拉牽伸模型在t1時刻發生一個事件，第1次對該活動實體的狀態產生改變，表示第k根纖維在t1時刻到達變速點。纖維變速的時刻根據每根纖維變速點位置不同而定，即該纖維以后羅拉速度運動了(t1-t0)時間后瞬間變為以前羅拉速度運動。此時，該纖維在牽伸區內屬于浮游纖維的類型，其受快速纖維的作用發生了提前變速行為，變成前羅拉速度。

3)纖維頭端到達前鉗口。羅拉牽伸模型會在t2時刻發生一個事件，再次改變該活動實體的狀態，表示該纖維頭端經過(t2-t1)時間到達前鉗口處。此時，該纖維屬于前纖維的類型，其到達前鉗口處后開始受到前羅拉的強控制。

4)纖維尾端移出牽伸區。該活動實體在t3時刻會產生最后一個離散事件，第3次改變系統狀態，表示該根纖維經過(t3-t2)時間后全部移出牽伸區，移出時間的長短根據每根纖維長度而不同。此時，該根纖維已經完成了羅拉牽伸過程，移出牽伸區且不再受羅拉控制，其運動速度為前羅拉速度。

從宏觀來看，整根須條經過牽伸區的過程如圖2所示。在須條截面中，相鄰纖維間隔長度不同的頭端距離，但均以相同的運動速度進入牽伸區。將每根纖維在牽伸區內的運動過程視為獨立隨機離散事件，其在運動過程中不會對周邊纖維的運動狀態產生直接的影響。每根纖維在牽伸過程中的不同時間以及不同位置發生變速行為，之后以前羅拉速度移出牽伸區完成牽伸過程。因此，將羅拉牽伸過程看作是一個纖維在須條長度方向上相對位置重新分配的過程，其目的是使須條的面密度減小并使纖維排列整齊。

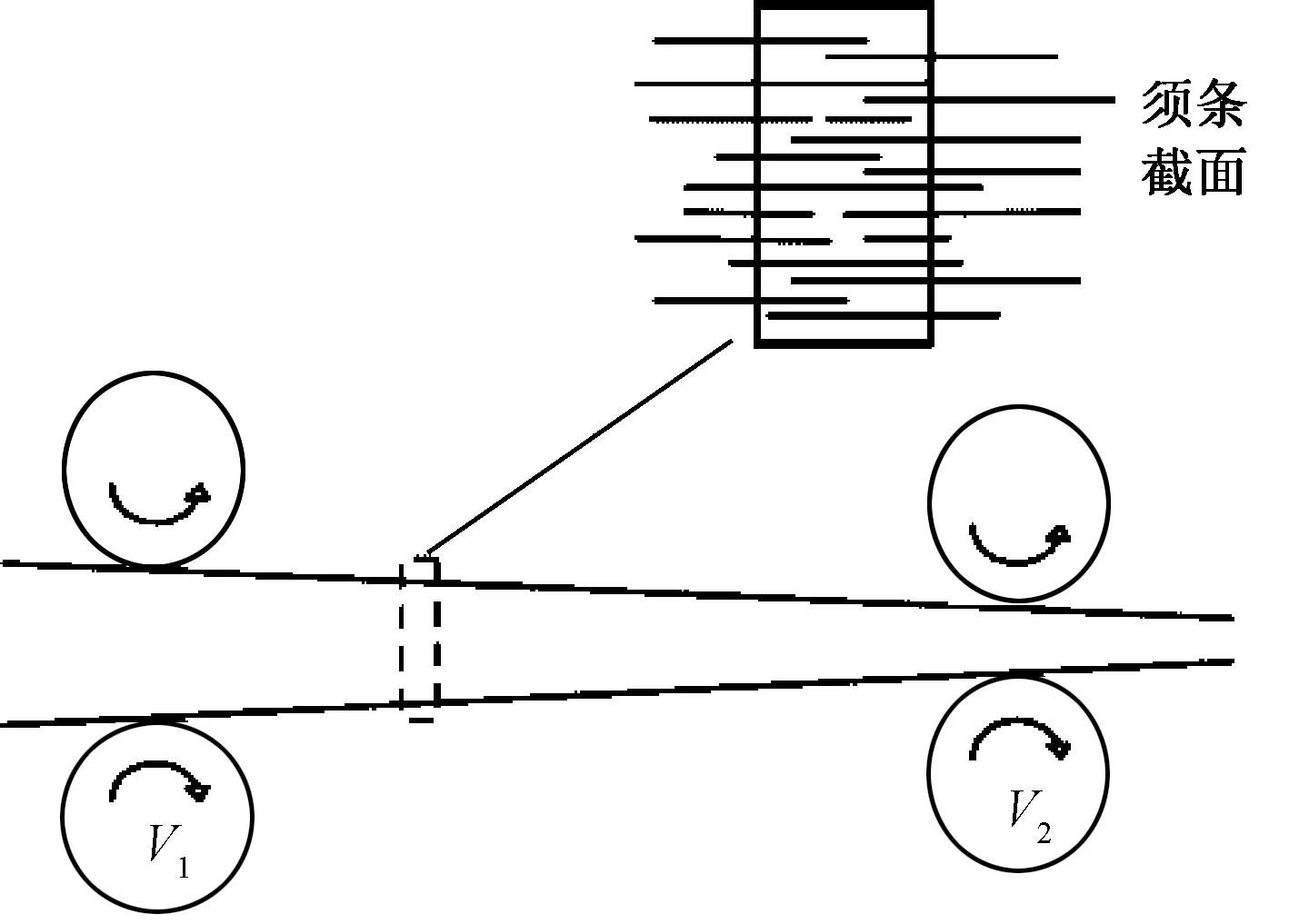
圖2 羅拉牽伸過程示意圖Fig.2 Schematic drawing of drafting process

以上描述了采用離散事件仿真理論建立羅拉牽伸模型的方法，與連續模型相比這種建模方式能夠更加準確地反映出須條的羅拉牽伸過程，其建模的優勢如下：1)將單根纖維作為研究對象，可在整個仿真計算過程中追蹤每根纖維的運動過程；2)將每根纖維在牽伸區內的運動過程視為獨立隨機離散事件，避免了考慮纖維之間復雜的相互作用關系；3)通過統計須條長度方向上某些截面內的纖維根數變化情況(如牽伸區內快速纖維和慢速纖維的數量等)來研究羅拉牽伸過程中纖維的運動規律，而非只討論單根纖維的運動規律；4)可結合紡織理論模擬羅拉牽伸過程中纖維的運動情況(如變速點分布、纖維長度分布等)，使建立的羅拉牽伸模型更加符合實際情況；5)該模型對纖維的參數要求比較少，其適用范圍比較廣。

1.2 模型的構成

上文內容詳細闡述了采用離散事件仿真理論建立羅拉牽伸模型的原理，但如果要實現該羅拉牽伸模型，還需要對仿真過程中的各個參數給出相應的算法和等式，以符合羅拉牽伸過程中的實際要求。該羅拉牽伸模型的輸入參數和輸出如圖3所示。該模型主要有6個輸入參數：L為纖維長度及分布，mm；P為牽伸區內纖維變速點與前鉗口的距離，mm；S為輸入須條定量，g/m；R為羅拉隔距，mm；后羅拉速度V1和前羅拉速度V2。其中，變速點分布可根據不同的紡織牽伸理論進行變化，其他輸入參數需結合實際情況取輸入值，該模型的輸出值為須條某些截面內的纖維根數以及不勻。

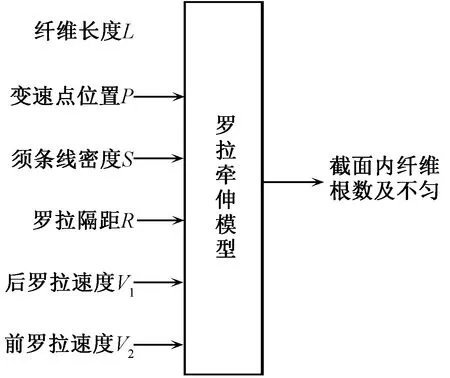
圖3 羅拉牽伸模型的輸入和輸出Fig.3 Input and output of roller-drafting model

根據圖1的方法，需要確定單根纖維在牽伸區內保持每種狀態的時間間隔以及下一根纖維到達的時間。具體實現該羅拉牽伸模型的算法如下。

1)第k根纖維的頭端在t0時刻進入牽伸區內，此時該根纖維以后羅拉速度V1運動。

2)第k根纖維在t1時刻變速，設纖維頭端到達變速點瞬間變為前羅拉速度，設其與前鉗口的距離為P，則該根纖維以后羅拉速度運動時間為T1=(R-P)/V1，其中R為羅拉隔距。

3)第k根纖維頭端在t2時刻到達前鉗口處，設前羅拉速度為V2，則該根纖維的頭端從變速點位置運動到前鉗口處所需的時間為T2=P/V2。

4)第k根纖維的尾端移出牽伸區：設該根纖維的長度為L，則整根纖維通過前羅拉所需的時間為T3=L/V2。

5)第k+1根纖維的頭端到達牽伸區內，第k+1根纖維與第k根纖維之間的時間間隔根據2根纖維在須條中排列的距離確定。假設在單位長度的須條內，有輸入須條的線密度S=L×F×V1/T，則可以推導出下一根纖維的頭端到達后羅拉鉗口處的平均時間間隔為T=(L×F)/(S×V1)。式中：L為纖維平均長度；F為纖維的線密度；V1為后羅拉速度；T為2根纖維間隔時間

6)重復算法2～5。

1.3 模型的實現

采用離散事件仿真語言GpssWorld實現該算法的過程如下：“GENERTATE”模塊用于產生活動實體來模擬纖維頭端進入牽伸區的過程，其產生活動實體的時間間隔的均值為T；“ADVANCE1”模塊用于延遲活動實體，來模擬纖維在牽伸區內以后羅拉速度運動的時間T1，同樣“ADVANCE2”模塊用于模擬纖維在牽伸區內以前羅拉速度運動的時間T2，“ADVANCE3”模塊用于模擬整根纖維移出牽伸區的時間T3；“TERMINIATE”模塊用于消亡活動實體，模擬纖維尾端移出前羅拉鉗口處的時刻，此時該活動實體的仿真過程結束。

該模型的仿真目的是為統計羅拉牽伸過程中須條截面內纖維數量的變化情況，而不是只研究單根纖維的運動過程，因此還需要采用統計模塊來統計某些截面內的纖維數量。模型中“TAB 1”到“TABn”模塊分別用于統計各自截面內的纖維根數及不勻，n根據需要統計的截面數量確定。一般“TAB 1”和“TABn”模塊分別用于統計輸入和輸出須條在一定的片段長度間的不勻值(條干不勻)，片段的長度可根據羅拉牽伸過程中實際的輸出要求而定，例如每隔1 cm、1 m和5 m片段長度統計其中的纖維根數。建立該模型的部分仿真程序如下：

GENERATET;按指數分布產生纖維

TAB 1;統計輸入牽伸區內的纖維根數

ADVANCE1T1;纖維以后羅拉速度運動的時間

ADVANCE2T2;纖維以前羅拉速度運動的時間

ADVANCE3T3;纖維尾端移出牽伸區的時間

TABn;統計輸出牽伸區的纖維根數

TERMINATE;仿真結束。

2 模型的驗證

為驗證該羅拉牽伸離散事件系統模型的正確性，需要同實際數據進行對比，因此，此部分驗證性仿真試驗的數據采用文獻[18]研究中的試驗數據和試驗條件，該文獻中提供的試驗條件具體內容如下。

試驗材料：粘膠纖維的線密度為1.7 dtex，長度為38 mm，6根須條并合。

試驗方法：羅拉隔距設置為44 mm，牽伸倍數分別為2、3、4、5、6；粘膠纖維普梳條定量分別為3.898、4.650、6.150、7.055 g/m，固定后羅拉速度為1 m/s。

程序運行50 s，后羅拉速度為1 m/s，因此相當于輸入50 m須條進行羅拉牽伸。模型仿真與試驗結果的須條條干不勻(CVm)如圖4所示。其中模型的統計結果為每隔8 mm的須條片段長度間的不勻率。隨著牽伸倍數的增大，輸出須條條干不勻也隨著增大；隨著輸入須條定量的增大，輸出須條條干不勻減小。

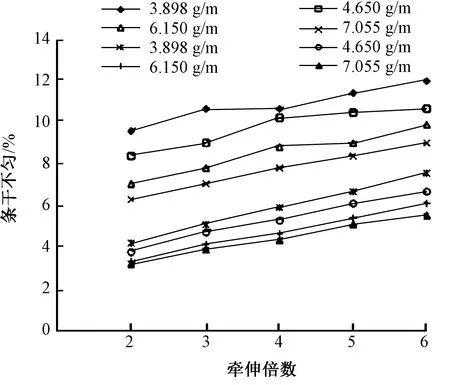
圖4 喂入定量和牽伸倍數對輸出須條條干不勻的影響Fig.4 Effect of input linear density and draft ratio on sliver irregularity

由于文獻[18]中沒有給出須條在牽伸之前的條干質量，所以模型的仿真過程中假設沒有輸入條干不勻的存在，須條中只有極限不勻，因此仿真結果會在數值上同試驗數據存在差距。比較圖中的數據可看出，仿真和試驗結果隨參數變化的趨勢是十分吻合的，因此可說明，采用離散事件仿真理論建立羅拉牽伸模型，仿真羅拉牽伸過程是可行的。

3 模型參數變化

該羅拉牽伸模型為多輸入多輸出模型，因此每個輸入參數的變化均對模型的輸出產生影響。下面以輸出條干不勻為模型的主要輸出結果，討論輸入參數對其影響情況，以反映出每個輸入參數在該羅拉牽伸模型系統中的重要程度。

在此仿真過程中，輸入參數分別為：纖維長度(等長38 mm)，線密度(1.7 dtex)，每根輸入須條定量(3.5 g/m)，須條并合根數(8根)，牽伸倍數(8倍)，固定前羅拉速度(5 000 mm/s)，羅拉隔距(42 mm)，須條中相鄰2根纖維間的頭端距離(固定)，變速點與前鉗口的距離(固定為12 mm)。輸出值為經過羅拉牽伸過程后輸出須條1 m片段長度內的條干不勻。在下面的分析討論過程中，將上述試驗條件作為基礎仿真條件，每次只改變其中的一個輸入參數，并保持其他輸入參數不變，以分別討論每個輸入參數對羅拉牽伸模型的影響大小。

3.1 纖維頭端分布

纖維的頭端距離是指須條內相鄰的前后兩根纖維間相距的長度，其主要反映了纖維在須條中的排列情況，纖維頭端分布是導致須條結構不勻的重要因素。理論上，由于移距偏差現象的存在，在經過羅拉牽伸過程后，2根纖維間的頭端距離會變大。因為該模型是以纖維的運動時間為基礎進行仿真的，所以須條中纖維頭端的距離對于該模型而言為下一根纖維頭端到達的時間間隔，故除纖維頭端距離以外還有纖維運動速度的影響因素，因此，在假設所有纖維運動速度相同的情況下，采用如下理論分布來模擬研究不同的纖維頭端分布對輸出條干不勻的影響效果：1)均勻分布(UNIFORM)；2)指數分布(EXPONENTIAL)；3)伽馬分布(GAMMA)。其中按照分布函數的特點，3種分布的均值均為T，均勻分布的方差為T2/12，指數分布的方差為T2，伽馬分布的方差為T2/4。另外，為考察時間間隔大小對輸出條干不勻的影響，將活動實體產生的時間間隔變成T到10T，仿真100 s后統計每種分布的仿真結果，結果如表1和圖5所示。

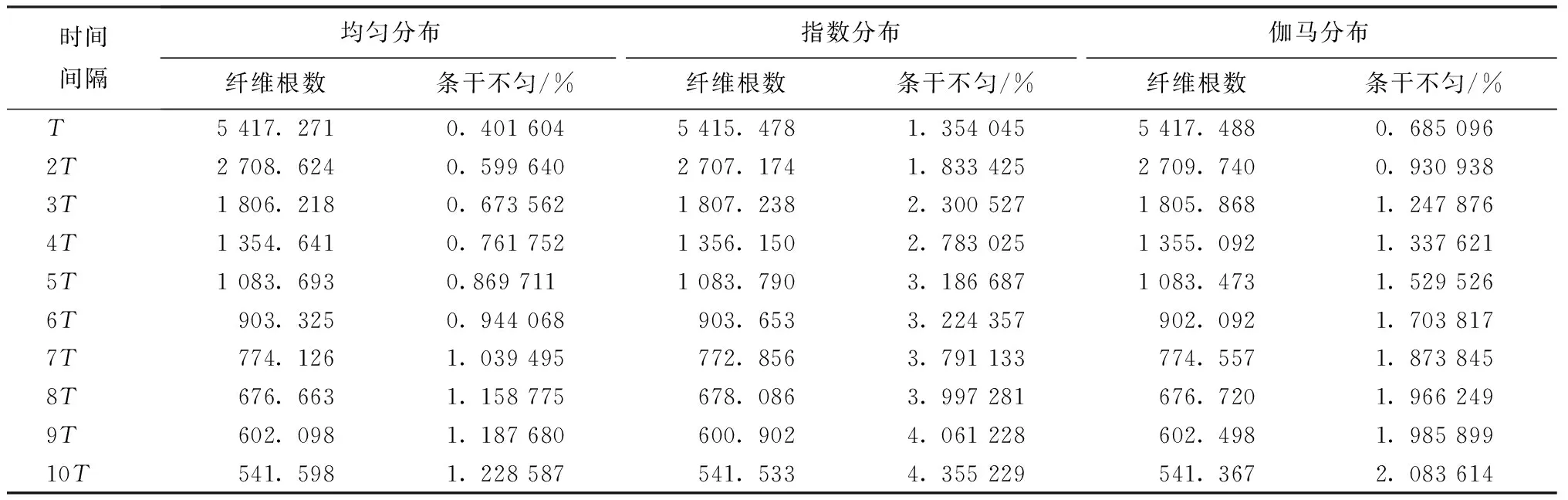
表1 不同纖維頭端分布對輸出條干質量的仿真結果Tab.1 Average number of fibers and sliver irregularities for different distributions and time intervals obtained by simulation

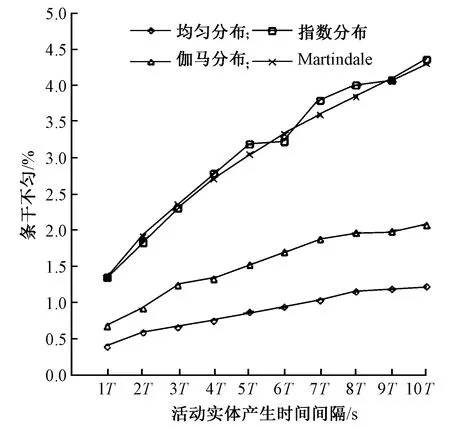
圖5 纖維頭端分布同須條條干不勻的關系Fig.5 Sliver irregularity versus different distributions of fiber front end

表1示出3種靜態分布下模擬纖維頭端分布對輸出條干不勻的情況。從中可看出，纖維根數與纖維頭端的分布沒有直接關系，只隨下一根纖維到達的時間間隔變大而減少。然而，從圖5中可明顯看出，纖維的頭端分布對條干不勻有顯著影響。3種靜態分布具有相同的變化趨勢，均隨著活動實體產生時間間隔的增大，輸出的條干不勻變大。另外，比較3種分布的方差大小可說明，隨著纖維頭端分布的方差增大，輸出須條中條干不勻的變化幅度也增大。因此通過仿真結果可說明，在相鄰兩根纖維的頭端距離保持恒定不變的情況下，須條內的條干不勻是最小的。

Martindale曾提出紗線截面內纖維根數的極限不勻公式：CV=N-0.5，其中N為截面內的平均纖維根數。一方面，仿真中當纖維頭端為指數分布時，該羅拉牽伸模型的仿真結果同極限不勻公式的計算結果吻合程度較好(見圖5)；另一方面，很多學者也指出，纖維頭端的實際分布非常接近于指數分布[1,16]，因此該羅拉牽伸模型的仿真過程中也采用指數分布作為須條中纖維頭端距離的分布。

3.2 變速點分布

在牽伸區內，以后羅拉速度運動的纖維稱為慢纖維，以前羅拉速度運動的纖維稱為快纖維。纖維的變速點是指浮游纖維由慢纖維變速成為快纖維時速度變化的位置。在理想牽伸條件下，假設纖維伸直平行且纖維長度相等，每根纖維都是在牽伸區內的某一截面處發生變速，故變速點分布為同一個截面。但是這種情況只能進行理論討論，實際中即使纖維整齊度很高也不會在牽伸區內的同一個位置變速，浮游纖維在變速的過程會受到很多因素的影響。根據牽伸工藝配置以及每根纖維的長度不同等因素，每根浮游纖維發生變速的位置不盡相同，會呈現出某種分布。由每根纖維的變速位置共同組成的變速點分布情況直接決定了須條在牽伸過程中的運動行為，從而會影響到牽伸后須條的條干質量。

因此，牽伸區內浮游纖維變速點的分布是羅拉牽伸理論研究中的重點[19- 20]，很多學者從不同角度進行了討論，也給出了各自纖維變速點分布情況的理論[21-24]。為驗證不同變速點分布理論對該羅拉牽伸模型的影響，本文采用3個變速點理論分布來模擬羅拉牽伸過程。假設x為牽伸區內纖維變速點距離前羅拉鉗口的距離，f(x)為纖維變速點的概率密度函數。

其中，指數分布是由Fujino和Kawabata[25]提出：

韋伯分布為：

對數指數分布由林倩[22]提出：

式中：k為形狀參數；λ為規模參數；μ和σ為正態分布的均值和標準方差。

保持模型其他仿真參數不變，分別在不同的輸入須條定量情況下，仿真3種變速點分布對輸出須條條干不勻的影響，結果如圖6所示。

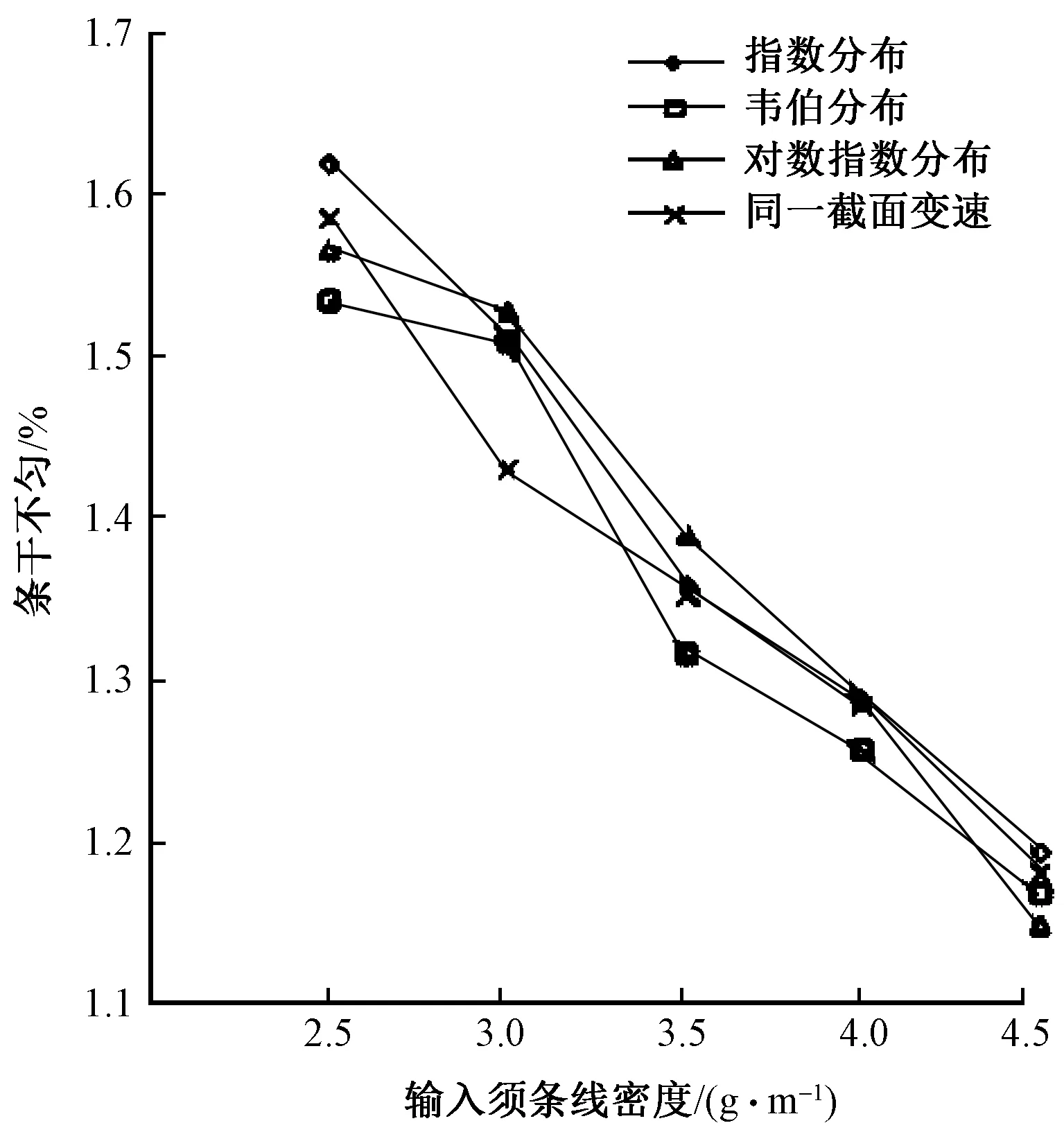
圖6 變速點分布對羅拉牽伸模型的影響Fig.6 Effect of distribution of VCP on sliver irregularity

采用不同的變速點理論進行仿真，雖然輸出須條條干不勻的數值大小不總是完全相等，但是其變化趨勢基本相同(見圖6)。這可以說明纖維變速點的理論分布不會對該羅拉牽伸模型產生重大影響，只是在輸出條干不勻的數值上有較小差別，其中韋伯分布的輸出條干不勻值最小。因此，為更加準確地模擬羅拉牽伸過程，不再固定變速點與前鉗口的距離，而是采用對數指數分布作為模擬牽伸過程的變速點分布。

3.3 須條定量

輸入須條定量大小可反映出羅拉牽伸模型中待牽伸須條的粗細情況，克重越高，則輸入須條越粗。在須條中纖維的伸直情況相同時，須條定量越高，截面內纖維根數越多，條干不勻越小。從圖6中可看出，隨著輸入須條定量的增大，輸出須條的條干不勻逐漸減小。

3.4 纖維長度及分布

很多學者已經指出，纖維長度對羅拉牽伸過程中條干不勻有重要的影響[21,26]。首先，纖維長度及分布會影響纖維在須條中的排列情況。同樣質量和粗細的須條，纖維長度越長，其中的纖維根數越少，條干不勻越大。其次，從理論上講，纖維長度及分布會影響纖維在牽伸區內變速的位置，纖維越長，長度分布越集中，則其在牽伸區內的變速點分布越集中且靠近前鉗口，因此，為研究該羅拉牽伸模型中纖維長度及其理論分布對模型仿真輸出條干不勻結果的影響情況，需要對該輸入參數做出如下設定。假設相同平均長度的纖維分別具有如下靜態分布：1)均勻分布(UNIFORM)；2)指數分布(EXPONENTIAL)；3)正態分布(NORMAL)；4)拉普拉斯分布(LAPLACE)。纖維平均長度取值范圍為25～45 mm，各分布函數的標準方差均為平均長度的10%，羅拉隔距為50 mm，其他條件不變，仿真運行100 s后輸出條干不勻結果如圖7所示。

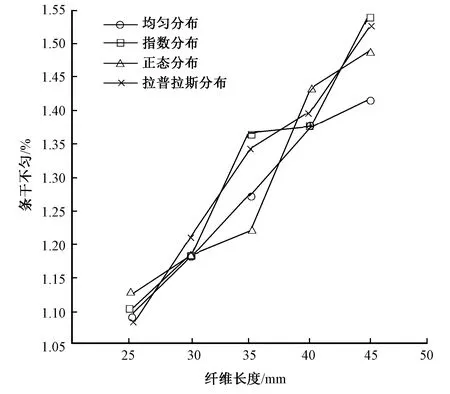
圖7 纖維長度與輸出條干不勻的關系Fig.7 Effect of fiber length on sliver irregularity

從圖7可看出，隨著纖維長度的增加，輸出須條條干不勻增加，但是纖維長度的分布形式對輸出須條條干不勻沒有顯著規律性的影響。因此從4條理論分布曲線的比較結果中可看出，纖維長度的大小是影響羅拉牽伸模型的重要因素，而纖維長度的分布形式對輸出須條條干不勻會產生影響，但并不是主要的影響因素。

4 結 論

本文在離散事件仿真的基礎上建立了一個羅拉牽伸模型，用于模擬須條的羅拉牽伸過程。首先結合紡織牽伸過程的特點和離散事件仿真理論，闡明了該羅拉牽伸模型的建模原理。然后通過與實際試驗數據的對比，驗證了該羅拉牽伸模型的正確性。最后，討論了各項參數變化對模型的影響，給出了合理的參數選取，并說明了輸入須條定量和纖維長度是影響該模型的主要因素。

該模型為用于模擬牽伸過程的基礎模型，模型中的各項參數以及纖維通過牽伸區的過程都可根據實際需要或者仿真要求進行改變。后續的研究中會在該羅拉牽伸模型的基礎上討論自調勻整的控制問題，通過改變羅拉速度來降低輸出條干不勻，優化牽伸過程，用于指導實際紡紗工藝。

FZXB

[1] MARTINDALE J G.A new method of measuring the irregularity of yarns with some observations on the origin of irregularities in worsted slivers and yarns [J].Journal of the Textile Institute,1945,36(3): 35-47.

[2] RAO J S.A mathematical model for the ideal sliver and its applications to the theory of roller drafting [J].Journal of the Textile Institute,1961,52(12): 571-600.[3] KORKMAZ Y A,BEHERY H M.Relationship between fiber fineness,break draft,and drafting force in roller drafting [J].Textile Research Journal,2004,74(5): 405-408.

[4] GROSBERG P.A cause of irregularity in roller drafting [J].Journal of the Textile Institute,1961,52(2): 91-5.

[5] ZHANG Z,YU C.Study on drafting force and sliver irregularity on drawing frame [J].Journal of the Textile Institute,2011,103(3): 1-7.

[6] LIN Q,OXENHAM W,YU C.A study of the drafting force in roller drafting and its influence on sliver irregularity [J].Journal of The Textile Institute,2011,102(11): 994-1001.

[7] HLAVA J.Stable model of textile sliver drafting process[C]// The 13th International DAAAM Symposium.Vienna：Citeseer,2002: 207-208.

[8] ISHIKAWA S,SHIMIZU J.Control of short-wave length irregularity of slivers [J].Journal of the Textile Machinery Society of Japan,1960,6(1): 31-34.

[9] YAMAGISHI T,KOYAMA E,KUROE H.A theoretical approach to the unstationary roller draft [J].Journal of the Textile Machinery Society of Japan,1956,2(2): 38-41.

[10] JOHNSON N A G.A computer simulation of drafting [J].Journal of The Textile Institute,1981,72(2): 69-79.

[11] DJIEV S N.Modeling a double-zone drafter as an object of control [J].Textile Research Journal,1994,64(8): 449-456.

[12] HUANG C,BAI J.Minimum variance control in leveling slivers [J].Textile Research Journal,2001,71(7): 621-625.

[13] HUH Y,KIM J.S.Modeling the dynamic behavior of the fiber bundle in a roll-drafting process [J].Textile Research Journal,2004,74(10): 872-878.

[14] HUH Y,KIM J S.Effects of material parameters and process conditions on the roll-drafting dynamics [J].Fibers and Polymers,2006,7(4): 424-431.

[15] KIM J S,CHERIF C,HUH Y.Dynamic stability and bifurcation in a bundle flow [J].Nonlinear Analysis: Real World Applications,2011,12(1): 343-352.

[16] CHERKASSKY A.Neural network meta-model of fibrous materials based on discrete-event simulation: part 1: discrete-event simulation model of one-dimensional fibrous material [J].Journal of the Textile Institute,2011,102(5): 442-454.

[17] CHERKASSKY A.Discrete-event simulation model of roll-drafting process [J].Journal of the Textile Institute,2011,102(12): 1044-1058.

[18] 張之亮.并條牽伸中牽伸力與纖維運動的研究 [D].上海：東華大學,2011：73-82.ZHANG Zhiliang.Study on the drafting force and fibers movement on drawing frame [D].Shanghai: Donghua University,2011：73-82.

[19] TAYLOR D S.The velocity of floating fibres during drafting of worsted slivers[J].Journal of the Textile Institute,1959,50(2): 233-236.

[20] YAO J,YE G,CHEN R.Modeling and simulating the motion of floating fibers during drafting [J].Journal of Donghua University,2006,32(4): 1-5.

[21] YAN G,YU C.The influence of fiber length distribution on the accelerated points in drafting: a new perspective on drafting process [J].Fibers and Polymers,2009,10(2): 217-220.

[22] LIN Q,OXENHAM W,YU C.Effect of accelerated point distribution on sliver irregularity: part 1: characterization of accelerated point distribution [J].Journal of the Textile Institute,2012,103(5): 549-557.

[23] YOSHIDA K,KATO M.A study on the accelerated-point distribution of floating fibers in drafting processes [J].Journal of the Textile Machinery Society of Japan,1975,21(4): 95-102.

[24] YAMASHITA S,KAWABATA S,KAWAI H.Study on blend irregularity caused by drafting,part 1: theoretical and experimental analysis [J].Journal of the Textile Machinery Society of Japan,1968,14(1): 1-11.

[25] FUJINO K,KAWABATA S.Method of analyzing problems on drafting [J].Journal of the Textile Machinery Society of Japan,1962,8(3): 12-21.

[26] ZEIDMAN M I,SUH M W,BATRA S K.A new perspective on yarn unevenness: components and determinants of general unevenness [J].Textile Research Journal,1990,60(1): 1-6.

Roller-drafting model based on discrete-event simulation

MA Baolong1，WANG Jun1,2

(1.CollegeofTextiles,DonghuaUniversity,Shanghai201620,China; 2.KeyLaboratoryofTextileScience&Technology,MinistryofEducation,DonghuaUniversity,Shanghai201620,China)

In order to study on the motion of fiber during roller-drafting process and predict the irregularity of slivers,a new approach was developed to simulate the roller-drafting process based on the discrete-event simulation.The roller-drafting discrete-event simulation model was established which combines the textile draft theory and discrete theory together.The influence of parameters on output slivers unevenness was discussed.The results indicated that this model could reflect the dynamic behavior of slivers and trace the motion of each fiber during roller-drafting process.In contrast with practical test data,it proved that this model could predict the variation of output slivers unevenness by drafting.After each parameter of established model was discussed,it pointed out that the fiber length and linear density of slivers were the most significant influence on roller-drafting process.

roller-drafting; unevenness; discrete-event simulation; simulation model

10.13475/j.fzxb.20151001608

2015-08-09

2015-11-02

麻寶龍(1989—)，男，博士生。主要研究方向為羅拉牽伸過程中的纖維運動。汪軍，通信作者，E-mail：junwang@dhu.edu.cn。

TS 101.9

A