四川卷與全國卷試題對比之“解三角形”

陳爽

摘 要： 從2017年起，四川普通高考各科全部使用全國統一命題試卷，四川卷與全國卷在數學試題上存在一些區別， “解三角形”常常與三角函數、不等式、平面向量、解析幾何、立體幾何等相互結合，求解與三角形有關的邊、角、面積等問題。本文從2013—2015年四川卷和全國卷I、II分析解三角形的考點，以及四川卷與全國卷在“解三角形”試題類型上的差異與相同點.

關鍵詞： 解三角形 考點分析 三角函數 不等式 實際問題

2016年將是四川最后一次自主命題，隨著高考改革的推進，從2017年起，四川普通高考各科全部使用全國統一命題試卷，對于數學這門學科而言，解三角形一直是高中數學中的重要內容，它具有較強的綜合性，如解三角形試題往往與平面向量、三角函數、不等式、立體幾何、解析幾何等相結合，題目靈活，能夠解決一些實際性問題等，因而成為高考試題的熱點和必考點[1].

1.解三角形的考點分析

解三角形就是求解出三角形的所有邊和所有角，正、余弦定理則是解三角形的一個有力工具，由于正余弦定理本身與三角函數相聯系，因此對于涉及解三角形中的求角、求邊的問題和判斷三角形的形狀等問題時，需要結合“正、余弦定理”、兩角和與差的三角函數、二倍角的三角函數、誘導公式等進行三角函數變換，多者相互結合求解三角形.

從表1和表2“2013—2015年四川卷和全國I、II卷解三角形所涉及內容”綜合來看，二者對于解三角形問題大部分涉及利用正、余弦定理結合三角函數求解三角形邊、角、面積等，少部分解三角形問題涉及不等式及向量方面的知識.從分值來看，四川卷每年基本都有一道解答題涉及解三角形，全國卷也將解三角形納入重點內容.從出題意圖來看，解三角形可以考查學生知識的綜合應用和靈活應用的能力.

2.三角函數與正、余弦定理結合解三角形

利用三角函數與正、余弦定理結合解三角形，雖然題型相對簡單，但是所涉及知識面較寬，尤其是三角函數中兩角和與差、二倍角的正弦、余弦和正切公式等誘導公式的靈活應用是學生的一大難點，同時解三角形時還隱藏著一些條件，比如三角形內角和180°，三角形三邊滿足兩邊之和大于第三邊、兩邊之差小于第三邊等.

例1（2013課標全國Ⅰ，理17）（本小題滿分12分）如圖，在△ABC，∠ABC=90°，AB=，BC=1，P為△ABC內一點，∠BPC=90°.

（1）若PB=，求PA

（2）若∠APB=150°，求tan∠PBA.

分析：根據已知條件，在△PAB中利用余弦定理即可求解PA，利用正弦定理即可解出tan∠PBA.

解：（1）由已知得∠PBC=60°，所以∠PBA=30°.

（2）設∠PBA=α，由已知得PB=sinα.

在△PBA中，由正弦定理得=，

化簡得cosα=4sinα.

所以tanα=，即tan∠PBA=.

小結：本題主要考查學生對正、余弦定理的理解和應用及一些較簡單三角函數誘導公式.

例2（2013四川，理17）（本小題滿分12分）在△ABC中，角A，B，C的對邊分別為a，b，c，且2coscosB-sin（A-B）sinB+cos（A+C）=-.

（1）求cosA的值；

（2）若a=4，b=5，求向量在方向上的投影.

分析：利用三角函數和與差的誘導公式和二倍角公式對已知條件進行化簡，即可求得cosA，最后結合正余弦定理求解出c的值即可求得向量在方向上的投影.

小結：本題主要考查學生應用正弦定理和余弦定理、三角函數中和與差、二倍角誘導公式及平面向量的投影等知識，所涉及知識面較寬，考查學生知識的綜合應用和靈活應用的能力.

3.不等式與解三角形結合

三角形中涉及求角、邊、面積范圍時，就會應用到不等式的相關知識，比如基本不等式等，在“解三角形”的過程中，要從研究角和邊的取值范圍開始，充分考慮三角函數值的符號和三角形兩邊之和大于第三邊、兩邊之差小于第三邊，三角形內角和180°，三角形的形狀等已知或隱含條件，盡可能縮小角和邊的取值范圍，只有這樣，才能避免產生增根或“擴大”所求變量的取值范圍[2].

例3（2014課標全國Ⅰ，理16）已知a，b，c分別為△ABC的三個內角A，B，C的對邊，a=2，（2+b）（sinA-sinB）=（c-b）sinC，則△ABC面積的最大值為？搖 ？搖.

分析：已知條件中（2+b）（sinA-sinB）=（c-B）sinC，既有邊又有正弦值，聯想到利用正弦定理，統一變量，再觀察化解后的形式和余弦定理相似，則可求出cosA，進而利用面積公式S=bcsinA求出面積的最大值.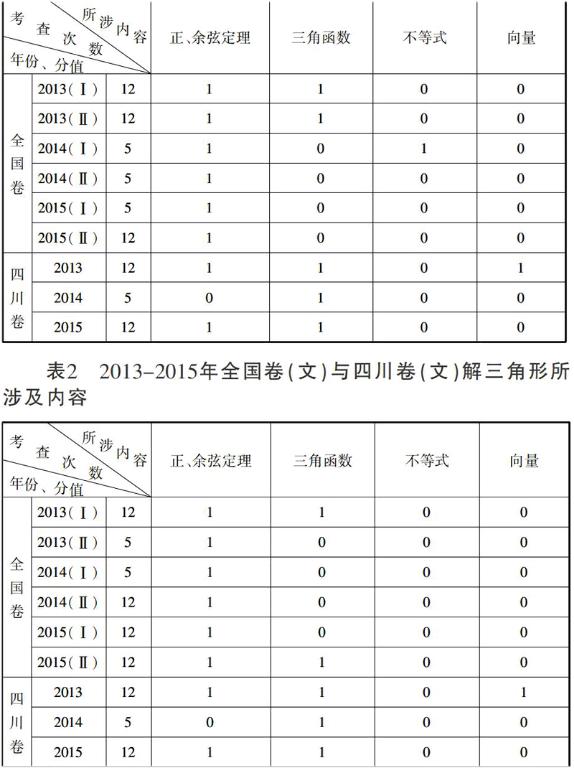

小結：本題主要考查學生對正弦定理和余弦定理的理解和綜合應用，以及解三角形與基本不等式的結合.

總之，解三角形雖然涉及內容較多，需要結合“正、余弦定理”、兩角和與差的三角函數、二倍角的三角函數、誘導公式等進行三角函數變換，進而求解三角形，但是從2013—2015年四川卷和全國卷I、II分析解三角形的考點來看，解三角形大部分涉及利用正、余弦定理結合三角函數求解三角形邊、角、面積等，少部分解三角形問題涉及不等式及向量方面的知識.學生需要靈活應用正余弦定理與三角函數的結合，才能真正掌握解三角形的相關知識.

參考文獻：

[1]楊衛劍，計惠方.2014年數學高考題大盤點——以“解三角形”為例[J].高中數理化，2015：3.

[2]馬俊華.例談高考數學試題中常見的“解三角形”問題[J].考試（高考教學版），2012：13.