考慮J2攝動的彈道導彈高精度彈道預報和誤差傳播分析

孫　瑜,吳　楠,孟凡坤,鄧啟正

(1.中國人民解放軍96669部隊,北京 102208;2.信息工程大學 導航與空天目標工程學院,鄭州 450001)

?

考慮J2攝動的彈道導彈高精度彈道預報和誤差傳播分析

孫瑜1,2,吳楠2,孟凡坤2,鄧啟正1

(1.中國人民解放軍96669部隊,北京 102208;2.信息工程大學 導航與空天目標工程學院,鄭州 450001)

摘要:為進行高精度的彈道導彈彈道預報和誤差傳播分析,分析了平根數法解攝動方程的解形式,提出了一種考慮J2攝動并包含短周期項的解析法,并將其用于彈道預報,結合無跡變換構造了彈道預報的誤差傳播分析方法,解決了解析法中開普勒根數求解過程不可微、偏導數矩陣難以計算的問題。仿真結果表明,將解析法用于彈道預報時,J2攝動短周期項導致的誤差達3個數量級,不可忽略;該算法預報的相對誤差只有不到5%,精度與高精度數值法相當,遠高于傳統解析法,但運算速度是后者的7倍,具有更好的效費比。

關鍵詞:彈道預報;無跡變換;J2攝動;解析法;短周期項

彈道預報與誤差傳播分析是戰略預警系統的重要研究內容。傳統的彈道預報方法通常有數值法和解析法兩類。數值法是在充分考慮導彈飛行過程中各種攝動因素的基礎上,建立導彈動力學方程,并采用一定的積分準則,利用數值逼近的方法計算彈道。文獻[1～2]基于導彈動力學方程采用不同的數值積分方法計算彈道,驗證了數值法的有效性。然而,這種方法預報的精確程度及計算速度與積分步長的選取有很大關系。小步長積分可以保證較高的預報精度,但是計算速度較慢;大步長積分計算速度快,但是預報精度不高。解析法是將導彈自由段飛行軌跡近似為橢圓彈道,通過計算開普勒根數進行彈道預報[3]。文獻[4～7]基于橢圓彈道理論,采用解析法實現彈道預報,并分別從時間和預報精度等方面提出優化算法。盡管采用了優化算法,但解析法的精度仍低于數值法,這是因為解析法將地球視作質點,沒有考慮地球是形狀不規則的扁球體。文獻[8～10]用考慮J2攝動的解析法計算人造衛星的軌道,因為人造衛星的運行周期很長,所以在解攝動方程的時候為了計算簡便,通常忽略短周期項。然而導彈與人造衛星截然不同的是導彈的飛行時間很短,它的短周期項能否忽略值得討論。

本文提出了一種考慮J2攝動并包含短周期項的解析法,并將其用于彈道預報,與數值法彈道預報進行仿真對比預報的精度及耗時。同時,在誤差傳播分析過程中,結合無跡變換(Unscented Transformation,UT)構造了彈道預報的誤差傳播分析方法,解決了解析法中開普勒根數求解過程不可微、偏導數矩陣難以計算的問題。

1考慮J2攝動并包含短周期項的彈道預報解析法

彈道導彈關機后進入自由段依靠慣性飛行,而自由段的高度一般在200 km以上,此時空氣阻力的影響可以忽略不計,導彈主要外力源為地球中心引力,可以將導彈繞地球的運動視為二體運動,從理論上可以認為其彈道為橢圓彈道,落點為橢圓彈道與地球的交點。解析法通過計算橢圓彈道的6個開普勒根數來預報導彈任意時刻的狀態。然而地球作為一個形狀不規則的扁球體,其重力場對自由段的影響很大,二階帶諧系數J2對彈道導彈自由段落點偏差的影響最大可達十幾km,四階帶諧系數J4對自由段落點偏差的影響可達數十m[11-12]。文獻[13]采用數值積分法，分析了不同積分步長、不同緯度和發射方位角下J2和J4項以及不同階數的擾動重力對導彈自由段落點的影響。J2項導致的攝動加速度約為10-3量級,而J4項攝動與大氣阻力、第三體引力、太陽光壓等其他攝動均為10-6量級及以下。若考慮J4項攝動,則大氣阻力、三體引力、太陽光壓等攝動均不能忽略,此時將大幅增加計算耗時。因此,綜合考慮預報的精度和耗時,本文只考慮J2項攝動的影響。

1.1J2攝動運動方程

地球是一個形狀不規則的扁球體,要精確地積分計算出其勢函數,必須知道地球的表面形狀及內部的密度分布。目前,通常采用球函數展開式推導出地球勢函數的標準表達式[14]:

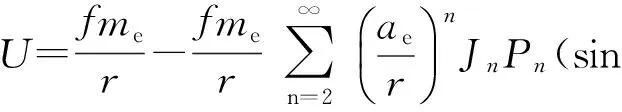
(Cnmcosmλ+Snmsinmλ)Pnm(sinφ)

(1)

式中:f為萬有引力常數;me為地球質量;r為地球外地心距;ae為地球赤道平均半徑;Jn為帶諧系數,Jn=-Cn0;n≠m時,Cnm,Snm稱為田諧系數;n=m時,Cnm,Snm稱為扇諧系數;Pn(sinφ)稱為勒讓德函數;Pnm(sinφ)稱為締合勒讓德函數;φ,λ為地球的地心緯度和經度。

物體繞地球運動的微分方程可寫成:

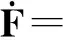
(2)

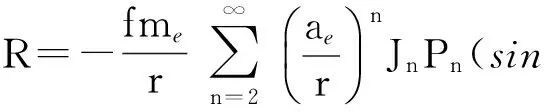
(Cnmcosmλ+Snmsinmλ)Pnm(sinφ)

(3)

當n=2時,即為考慮J2項攝動,取J2=1.082 63×10-3。

以6個開普勒根數為基本變量的拉格朗日型攝動運動方程[15]為

(4)

式中:a為軌道半長軸;e為偏心率;i為軌道傾角;Ω為升交點赤經;A為近地點幅角;M為平近點角;ω為平均角速度。設σ=(aeiΩAM)為開普勒根數構成的向量。

角析法中,平均根數法解攝動運動方程的特征是將攝動變化中不同性質的項區分開,相應的冪級數解的形式為

(5)

式中:

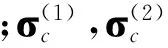
1.2開普勒根數轉移

對于衛星而言,由于其在軌運行時間長,在計算其攝動運動方程時,為了計算簡便通常忽略短周期項。對于彈道導彈,其飛行時間很短,所以在計算彈道導彈的攝動運動方程的時候不能忽略短周期項。而對于具體取到多少階的攝動解,則要取決于預報的精度需求。文獻[13]分析了不同階數對彈道導彈自由段落點的影響,中低階部分的影響從幾十m到數百m不等,對于自由段射程約6 000km的彈道導彈,考慮到30階左右可以達到m級的計算精度。本文重點在于綜合考慮預報的精度和預警時間,因此本文只考慮一階攝動解:包括所有的一階攝動項(長期項、長周期項和短周期項)和二階長期項。

考慮J2項攝動的平均根數法一階解完整結果如下:

(6)

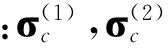
2基于無跡變換的誤差傳播分析

計算協方差矩陣時,純粹的解析法需要計算笛卡爾坐標對開普勒根數的偏導數矩陣以及開普勒根數的轉移矩陣,然而在計算開普勒根數轉移矩陣時會出現一個問題:如果考慮短周期項,則開普勒根數求解過程不可微,偏導數矩陣難以計算;如果不考慮短周期項,計算轉移矩陣所用的模型就與狀態方程中所用的模型不一致,得到的解是完全錯誤的,這個結論在文獻[16]中得到證實。而UT用采樣點來近似狀態向量的后驗概率密度,結合UT的解析法在對彈道導彈進行誤差傳播分析時,就不需要計算笛卡爾坐標對開普勒根數的偏導數矩陣以及開普勒根數的轉移矩陣。

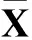
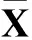
(7)

(8)

通過橢圓彈道理論計算每個χ點對應的開普勒根數σ,然后考慮J2攝動采用平根數法解拉格朗日攝動運動方程,計算出t時刻對應的開普勒根數σt。通過這些非線性變換得到樣點的輸出:

Ψj=f(χj)j=0,1,…,12

(9)

最后,計算t時刻位置速度的均值和協方差矩陣:

(10)

基于UT變換來處理協方差矩陣的非線性傳遞,可以避開計算笛卡爾坐標對開普勒根數的偏導數矩陣以及開普勒根數的轉移矩陣,并且對任意t時刻的協方差矩陣可以直接計算,不需要計算t時刻之前的協方差矩陣,能夠有效提高彈道預報效率。

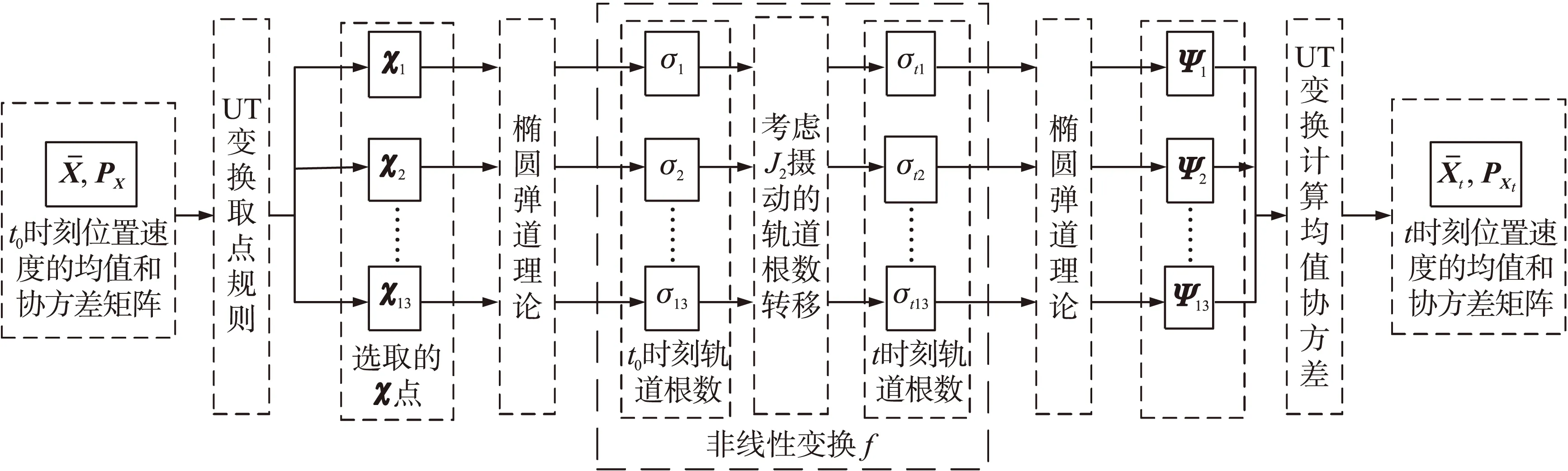
圖1　系統流程框圖

3仿真分析

仿真將通過普通解析法、基于UT的解析法和數值法對彈道導彈自由段進行預報,忽略空氣阻力等其他攝動力,只考慮J2攝動的影響。普通解析法是直接解算攝動運動方程,通過計算開普勒根數變化率,解算出預報終點的位置速度;基于UT的解析法即上文所提的方法;數值法是通過對目標的運動方程進行積分計算彈道的方法,數值積分采用四階龍格-庫塔算法,仿真步長設為1s。首先分析解析法中短周期項對彈道預報的影響,然后分析基于UT的解析法計算的協方差矩陣和普通解析法進行蒙特卡洛仿真得到的均方根誤差的一致性,最后對比分析解析法和數值法的預報精度和運算速度。設在地心慣性坐標系下,探測到導彈在自由段500s時刻的位置為x=2 163 451m,y=-6 342 006m,z=2 191 877m,速度vx=594.31m/s,vy=711.49m/s,vz=5 453.41m/s,協方差為

預報終點t=1 287s。

3.1短周期項對彈道預報的影響

有短周期項的解析法與數值法的均值差變化情況及無短周期項的解析法與數值法的均值變化情況如圖2所示。

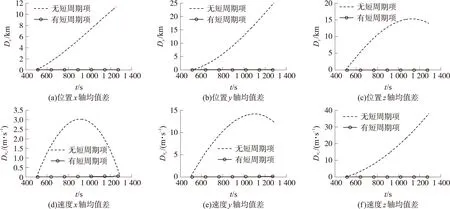
圖2　均值之差的變化情況

從圖2中可以看到,無短周期項的解析法與數值法計算的均值差在位置的x軸、y軸方向及速度的z軸方向均成發散趨勢,速度的x軸、y軸方向及位置的z軸方向有成周期變化的趨勢。位置的x軸方向終點處偏差約12km,y軸方向終點處偏差達到25km,z軸方向偏差最大達到15km,終點處約14km;速度的x軸方向偏差最大有3m/s,終點處為0.12m/s,y軸方向偏差最大達到14m/s,終點處為12.38m/s,z軸方向終點處偏差為38.08m/s。而與無短周期項相比,考慮了短周期項的解析法與數值法之差則小得多,接近于0。t=1 287s時刻,均值差的具體結果如表1所示。由此可見,由于彈道導彈飛行時間短,短周期項對彈道預報的影響很大,位置偏差能夠達到3個數量級,所以在進行高精度彈道預報時不能忽略短周期項。

表1　均值之差仿真結果

3.2誤差一致性分析

采用UT變換解析法計算的標準差和普通解析法1 000次蒙特卡洛仿真得到的均方根誤差的變化情況如圖3所示。

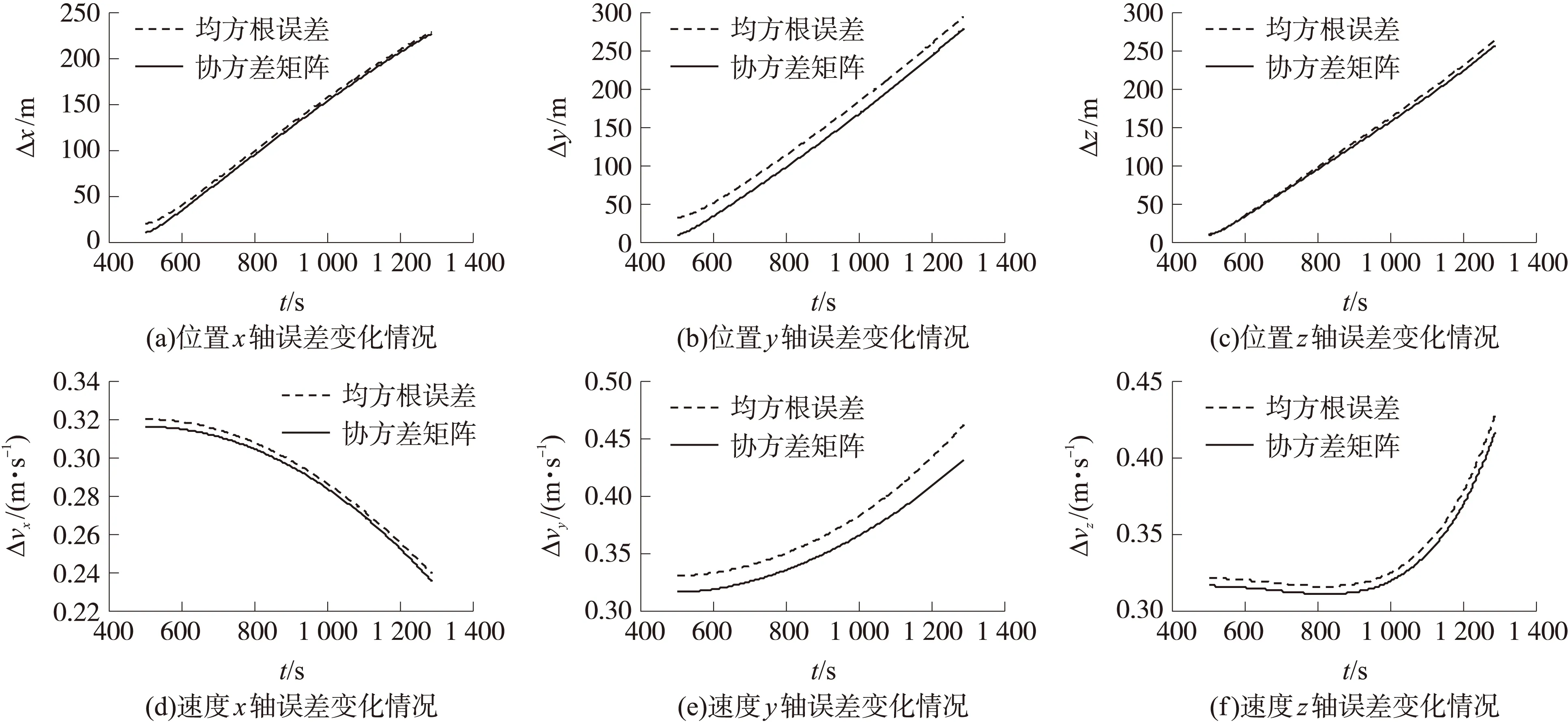
圖3　普通解析法均方根誤差與基于UT變換解析法的標準差變化情況

從圖3中可以看到,二者的趨勢基本相同,且預報的協方差位置和速度均略小于均方根誤差。在預報的終點處,位置x軸的相對誤差為1%,位置y軸的相對誤差為5.7%,位置z軸的相對誤差為3.03%,速度x軸的相對誤差為1.7%,速度y軸的相對誤差為7.1%,速度z軸的相對誤差為2.6%?？梢?二者的相對誤差非常小,而UT變換計算的協方差矩陣比蒙特卡洛仿真計算的均方根誤差略小,是因為協方差矩陣是截斷誤差,忽略了高階項,屬于正常誤差,可以說二者是一致的。

3.3彈道預報和誤差傳播分析

圖4給出了考慮J2攝動解析法的標準差和數值法1 000次蒙特卡洛仿真得到的均方根誤差的變化情況。從圖中可以看到,二者的變化趨勢基本一致,解析法的協方差矩陣在x軸、y軸方向的位置和速度均略大于數值法的均方根誤差,在z軸方向的位置和速度均略小于數值法的均方根誤差,說明解析法的精度在x軸和y軸略低于數值法,而z軸略高于數值法。在預報的終點處,位置x軸的相對誤差為4.6%,位置y軸的相對誤差為4.2%,位置z軸的相對誤差為2.5%,速度x軸的相對誤差為4.8%,速度y軸的相對誤差為3.5%,速度z軸的相對誤差為1.1%。無論位置還是速度,兩種方法的相對誤差都不超過5%,說明解析法和數值法的預報精度相當,基本在同一數量級。

考慮J2攝動的解析法的總耗時為128.075ms,其中每個χ點的總耗時為9.851ms。每個χ點在傳播的過程中,500s初始時刻的位置速度轉換成開普勒根數的耗時最大,為4.478ms,占其傳播總耗時的45%左右;計算500s時刻平均根數的耗時為2.001ms,占20%左右;計算長期項耗時為0.883ms,占9%左右;計算1 287s時刻的平均根數的耗時為0.616ms,占6%左右;計算短周期項和長周期項的耗時分別為0.755ms和0.698ms,分別占8%和7%左右?？梢?在解析法中位置速度與開普勒根數之間的轉換耗時最大。數值法積分步長為1s,每步長的平均耗時約為1.048ms,預報自由段時長為788s,數值法總耗時為826.602ms,是解析法的7倍左右。

預報飛行時長800s左右的彈道得到相同級別的精度,數值法計算耗時可以達到考慮J2攝動解析法的7倍左右。原因是數值法在計算任意時刻導彈狀態的時候,需要按照一定的步長逐步積分,耗時與所選取的步長成反比,保證一定的精度就需要選取較小的步長,而以耗時的增加為代價;而解析法中,在觀測到導彈初始狀態后,就能夠快速計算出彈道6個開普勒根數的變化情況,只要給出任意時刻點,就可以直接計算導彈在該時刻的狀態,所以計算速度快。

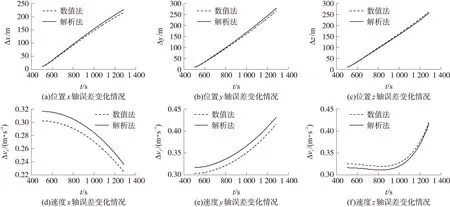
圖4　數值法均方根誤差與考慮J2攝動解析法標準差的變化情況

綜上所述,總結得到如下結論:

①由于彈道導彈飛行時間短,短周期項對彈道預報影響很大,位置偏差能夠達到3個數量級,在進行高精度彈道預報的時候不能忽略;

②結合UT的解析法進行誤差傳播分析,能夠有效避開計算笛卡爾坐標對開普勒根數的偏導數矩陣以及開普勒根數的轉移矩陣;

③考慮J2攝動的解析法與積分步長為1s的數值法相比,彈道預報的精度在同一數量級,并且在預報800s左右的彈道時,耗時只有數值法的1/7左右。

4結束語

本文通過仿真對解析法和數值法在彈道預報中的性能進行了對比分析。解析法在進行誤差傳播分析時結合UT,能夠有效避開計算笛卡爾坐標對開普勒根數的偏導數矩陣以及開普勒根數的轉移矩陣。傳統的解析法只是簡單地近似成二體問題,沒有考慮其他攝動因素,所以計算精度不高;而考慮了J2攝動之后的解析法,計算精度和誤差傳播發散程度都與積分步長為1s的數值法相當,在預報800s左右的彈道時運算速度是數值法的7倍左右。但是考慮J2攝動的解析法在彈道預報中,不能夠像計算衛星軌道一樣簡單地忽略短周期項,短周期項對彈道預報影響很大,在進行高精度的預報彈道時不能忽略。

參考文獻

[1]張龍杰,謝曉方.通用變步長彈道仿真方法研究[J].彈道學報,2011,23(2):42-46.

ZHANG Long-jie,XIE Xiao-fang.Research on general variable step-size ballistic simulation method[J].Journal of Ballistics,2011,23(2):42-46.(in Chinese)

[2]程誠,張小兵.某制導炮彈二位兩相流內彈道性能分析與數值模擬研究[J].兵工學報,2015,36(1):58-63.

CHENG Cheng,ZHANG Xiao-bing.Two-dimensional numerical simulation on two-phase flow interior ballistic performance of a guided projectile[J].Acta Armamentarii,2015,36(1):58-63.(in Chinese)

[3]張毅,楊慧耀,李俊莉.彈道導彈彈道學[M].長沙:國防科技大學出版社,1999.

ZHANG Yi,YANG Hui-yao,LI Jun-li.Ballistic missile ballistics[M].Changsha:National University of Defense Technology Press,1999.(in Chinese)

[4]李森,劉紅軍,程仲.提高彈道導彈落點預報精度方法[J].電子科技,2012,25(9):85-87.

LI Sen,LIU Hong-jun,CHENG Zhong.Improvement of TBM’s impact-point prediction precision[J].Electronic Sci & Tech,2012,25(9):85-87.(in Chinese)

[5]沈慧娜,徐振來.提高彈道導彈落點預報精度的動弧平滑平均法[J].現代雷達,2009,31(7):55-58.

SHEN Hui-na,XU Zhen-lai.Moving arc smoothing averaging algorithm for improving the prediction precision of ballistic missile impact point[J].Modern Radar,2009,31(7):55-58.(in Chinese)

[6]劉仁,王愛華,郭桂治.基于關機點狀態的戰術彈道導彈落點估計[J].空軍工程大學學報,2010,11(1):27-30.

LIU Ren,WANG Ai-hua,GUO Gui-zhi.Impact point estimation of tactical ballistic missile based on the state of burnout point[J].Journal of Air Force Engineering University,2010,11(1):27-30.(in Chinese)

[7]劉彥君,喬士東,黃金才,等.一種高精度彈道導彈落點預測方法[J].彈道學報,2012,24(1):23-26.

LIU Yan-jun,QIAO Shi-dong,HUANG Jin-cai,et al.A method of impact point prediction of ballistic missile[J].Journal of Ballistics,2012,24(1):23-26.(in Chinese)

[8]劉林.一種人造地球衛星的攝動計算方法[J].天文學報,1975,16(1):5-80.

LIU Lin.A calculating method of perturbation of artificial satellite[J].Acta Astronomica Sinica,1975,16(1):5-80.(in Chinese)

[9]曹文華,李傳榮,李子揚,等.基于攝動模型的衛星軌道預測算法精度評估[J].遙感信息,2012,27(6):21-27.

CAO Wen-hua,LI Chuan-rong,LI Zi-yang,et al.Accuracy assessment of satellite orbit prediction based onJ2perturbation model[J].Remote Sensing Information,2012,27(6):21-27.(in Chinese)

[10]張俊.基于開普勒二體運動修正地球扁率J2攝動項算法[J].航天控制,2014,32(6):22-25.

ZHANG Jun.Correction algorithm ofJ2perturbations of the earth oblateness based on Kepler two-body motion[J].Aerospace Control,2014,32(6):22-25.(in Chinese)

[11]鄭偉,湯國建.上升段引力常數變化及其對彈道導彈運動的影響[J].導彈與航天運載技術,2008,295(3):12-14.

ZHENG Wei,TANG Guo-jian.Gravitation constant variety in ascend phase and its effect on ballistic missile[J].Missile and Space Vehcile,2008,295(3):12-14.(in Chinese)

[12]鄭偉,湯國建.彈道導彈自由段解算的等高約束解析解[J].宇航學報,2007,28(2):269-272.

ZHENG Wei,TANG Guo-jian.Contour restricted analytical solution for free flight trajectory of ballistic missile[J].Journal of Astronautics,2007,28(2):269-272.(in Chinese)

[13]馮偉,劉根友,郝曉光.重力場對彈道導彈自由段落點影響的仿真分析[J].測繪科學,2009,34(5):118-120.

FENG Wei,LIU Gen-you,HAO Xiao-guang.Simulated analysis of the effect of gravity field to the fall point in free flight trajectory of ballistic missile[J],Science of Surveying and Mapping,2009,34(5):118-120.(in Chinese)

[14]賈沛然,陳克俊,何力.遠程火箭彈道學[M].長沙:國防科技大學出版社,1993.

JIA Pei-ran,CHEN Ke-jun,HE Li.Long-range rocket ballistics[M].Changsha:National University of Defense Technology Press,1993.(in Chinese)

[15]李濟生,葉杰,王家松,等.航天器軌道確定[M].北京:國防工業出版社,2003.

LI Ji-sheng,YE Jie,WANG Jia-song,et al.Determination of spacecraft[M].Beijing:National Defense Industry Press,2003.(in Chinese)

[16]MAY J A.A study of the effects of state transition matrix approximations,NASA CP 21123[R].1980.

Analysis on High Precision Trajectory Prediction and Error Propagation of Ballistic Missile ConsideringJ2Perturbation

SUN Yu1,2,WU Nan2,MENG Fan-kun2,DENG Qi-zheng1

(1.Unit 96669 of PLA,Beijing 102208,China;2.College of Navigation and Aerospace Target,Information Engineering University,Zhengzhou 450001,China)

Abstract:To carry out high-precision trajectory prediction and error propagation analysis of ballistic missile,the solution form of mean element algorithms for perturbation equation was analyzed,and an analytical algorithm consideringJ2perturbation and containing the short period term was proposed for trajectory prediction.By constructing the error propagation analysis method of trajectory prediction based on unscented transform,the problem that the Kepler elements is not differentiable and the partial derivative matrix is difficult to calculate was solved.The simulation results show that the error caused by theJ2perturbation short period term,which can not be ignored,reaches 3 orders of magnitude when analytical algorithm is applied in the trajectory prediction.The relative error predicted by the proposed algorithm is only less than 5%,and the precision is far higher than the precision of traditional analytical algorithm,which is comparable with the precision of high-precision numerical algorithm,but the operation speed is 7 times of the latter,and the algorithm has a better effectiveness-cost ratio.

Key words:trajectory prediction;unscented transformation;J2perturbation;analytical algorithm;short-period term

收稿日期:2015-12-30

作者簡介:孫瑜(1986- ),男,助理工程師,碩士,研究方向為空天目標預警信息處理。E-mail:woshizhongsy@163.com。

中圖分類號:TJ760.1

文獻標識碼:A

文章編號:1004-499X(2016)02-0018-07