無粘結預應力簡支試驗梁變形和應力分析
張冬久
(中鐵第五勘察設計院集團有限公司東北分院,黑龍江 哈爾濱 150006))
?
無粘結預應力簡支試驗梁變形和應力分析
張冬久
(中鐵第五勘察設計院集團有限公司東北分院,黑龍江 哈爾濱150006))
摘要:無粘結預應力技術在工程中的應用越來越廣泛,對無粘結預應力結構的研究也越來越重要。以1片試驗梁為研究對象,通過分級施加豎向荷載和預加力,測試各級荷載作用下試驗梁的變形和應力(應變),采用ANSYS有限元軟件建立試驗梁的有限元分析模型,
關鍵詞:無粘結預應力;簡支梁;試驗;變形;應力
1試驗設計
1.1試驗梁設計
試驗梁截面尺寸為200 mm×200 mm,梁總長為3 100 mm,計算跨徑為3 000 mm,預應力筋采用1束7Φs15.2 mm的1 860級鋼絞線,公稱截面面積為139 mm2,錨墊板采用200 mm×200 mm×10 mm的Q235鋼板,底部和頂部主筋分別采用2根直徑為12 mm的HRB335鋼筋,箍筋采用直徑為8 mm的R235鋼筋,設計混凝土標號為C30,試驗梁預留管道在預應力筋張拉后不灌漿,確保預應力筋處于無粘結狀態,縱向預應力筋為通過截面形心的直線預應力筋。
1.2加載方案
(1)豎向荷載
對試驗梁進行靜力試驗,對混凝土應變、鋼筋應變和變形進行測試。試驗梁在豎向荷載作用下不僅會產生彎矩,而且會產生剪力,為減少剪力的影響,采用兩點對稱加載的方式,本試驗重點研究剪力為零的“純彎段”內梁的正截面受力狀態和變形規律。扣除結構自重所產生的變形和應變,分析試驗梁在各加載階段的變形和應變情況。施加集中荷載模擬梁的不同恒載作用,同時要控制豎向集中荷載的大小,保證試驗梁在試驗過程中不產生裂縫、不失穩,豎向荷載位置,其中L表示試驗梁的計算跨徑,F表示豎向恒載,采用三級加載,每級遞增2 kN,分別為2 kN、4 kN、6 kN。可以看出,試驗加載距離兩側支點各L/3,中間的L/3為理論“純彎段”。
由于混凝土梁中的微小裂縫會對梁的靜力參數產生很明顯的影響,因此明確多大的預加力將使梁中產生拉應力及裂縫至關重要。同時,在確保預加力不使預應力混凝土簡支梁失穩及受壓區混凝土破碎的情況下,計算張拉預加力時的最大值,通過計算可以得出試驗梁最大預加力為123.5 kN,在試驗過程中,預加力采用120 kN作為最大值。
預應力筋從0 kN開始,分級張拉,在每級預加力作用下再分級施加豎向荷載。豎向荷載加載到預定級別時卸載,再張拉下一級預加力。每兩級豎向加載之間的時間間隔不少于10 min,每兩級預加力之間時間間隔不少于45 min。
2有限元模型
2.1無粘結預應力模擬
在預應力混凝土梁中對無粘結的預應力的模擬通常有下面的兩種方法:等效荷載法和實體力筋法。等效荷載法最突出的特點是模型的建立簡便,預應力鋼筋的布置形式不予以考慮,網格劃分簡潔、便利,程序比較容易收斂,且可以直觀的表現出預應力工作時預應力梁的整體響應效果,大部分運用于桿系結構的研究;等效荷載法最明顯的缺點就是預應力筋在混凝土梁內部布置時不能對預應力的分布和方向進行模擬。實體力筋法模擬預應力混凝土梁最常用的方法有初始應變法和降溫法。初始應變法通常不能考慮預應力損失,每個單元的實常數各不相等,工作量很大。降溫法是給預應力筋單元施加溫度值來模擬預應力值,溫度值可以利用張拉預應力值來反算,降溫法來模擬張拉預應力簡單易行,在外力共同作用時,也可考慮外力與預應力的共同作用,同時也能模擬外力作用對預應力筋的影響。
通過比較兩種方法的優缺點,結合試驗梁的實際情況,本論文無粘結預應力試驗梁采用實體力筋法中的降溫法來模擬預應力變化。溫度改變值按下式計算
式中:σ為預應力鋼筋的張拉應力;E為預應力鋼筋自身的彈性模量;α為預應力鋼筋自身的線膨脹系數。
2.2有限元模型建立
試驗梁有限元模型采用ANSYS軟件建立,混凝土采用SOLID65模擬,鋼筋及預應力筋采用LINK8模擬。
3結果分析
3.1變形分析
圖1和圖2反映出試驗梁在豎向荷載作用下產生向下的變形,變形形狀呈現為拋物線形。
實測、有限元計算、公式計算的試驗梁在不同預加力情況下變形隨預加力的變化數值見表1,變化情況如圖4所示。
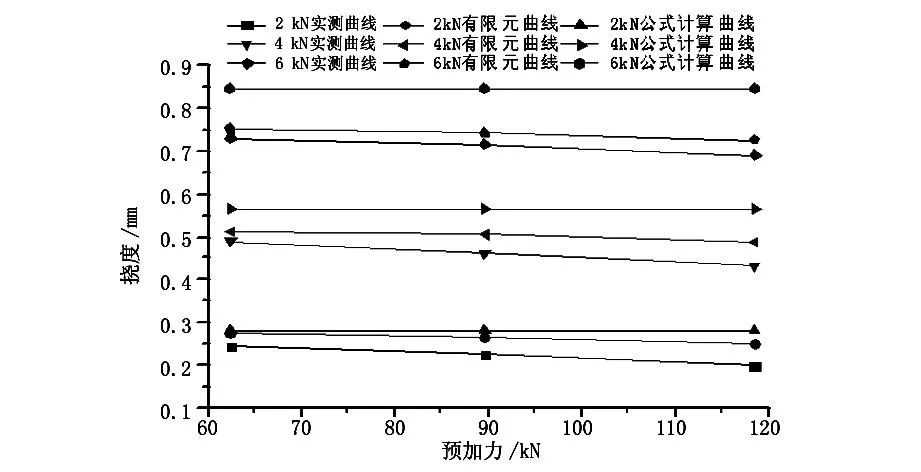
圖1 變形—預加力曲線圖
從表1和圖3中可以看出:在各級豎向荷載作用下,公式計算變形值最大,有限元計算變形值次之,實測變形值最小,進而得出采用公式計算變形偏于保守,進行結構設計是偏于安全的;在同級豎向荷載作用下,預加力的增加會導致試驗梁的變形值減小,這是因為預加力增加使截面的剛度增大,變形隨預加力增加減小幅度不大;在同一級預加力作用下,變形隨豎向荷載的增大而增大,例如當預加力為90 kN時,2 kN、4 kN、6 kN豎向荷載作用下,實測變形值分別0.225 mm、0.460 mm、0.715 mm,
3.2應力(應變)分析
在豎向荷載作用下試驗梁的應變情況示意圖,如圖2~圖3所示。
圖5反映出在豎向荷載作用下,試驗梁跨中截面下緣承受拉應力,上緣承受壓應力。從圖6中可以看出試驗梁左右支點各L/3范圍,上緣鋼筋和下緣鋼筋的應力分布圖呈現為對稱的三角形,中間段L/3范圍應力分布圖呈現為對稱的矩形,也就是“純彎段”,在整個跨徑L范圍應力呈現為低腰梯形,其中上緣鋼筋為壓應力,下緣鋼筋為拉應力。

圖2 試驗梁跨中應變示意圖
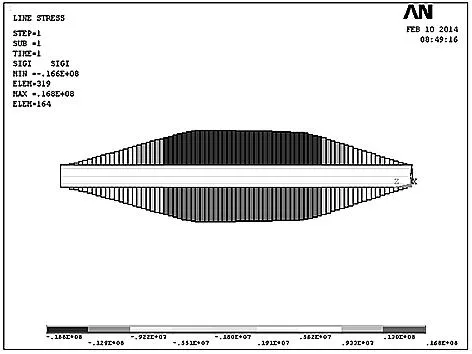
圖3 試驗梁縱向鋼筋應變示意圖
試驗梁在不同預加力情況下應變隨預加力值的變化曲線示意圖,如圖4~圖7所示,圖中負值表示壓應變,正值表示拉應變。
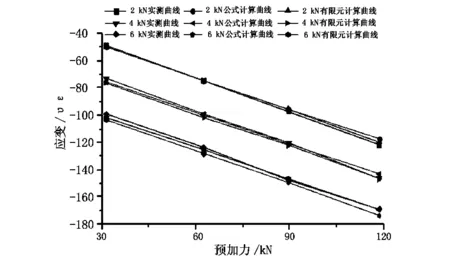
圖4 試驗梁頂面混凝土應變—預加力曲線圖
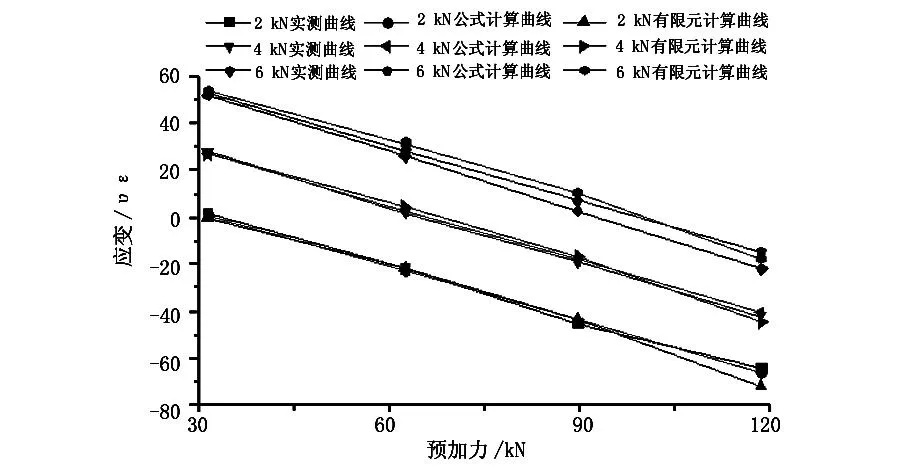
圖5 試驗梁底面混凝土應變—預加力曲線圖
從圖2和圖3中可以看出:在各級豎向荷載作用下,試驗梁頂面和底面混凝土實測應變值、公式計算應變值與有限元計算應變值相差很小,三者相符;在同級豎向荷載作用下,隨著預加力的增加,試驗梁頂面混凝土的壓應變不斷增大,表現為線性變化,試驗梁底面混凝土的應變由拉應變轉變為壓應變,變化趨勢也表現為線性,例如當豎向荷載為4 kN時,預應力從30 kN增大到120 kN的過程中,頂面混凝土應變由-73 με變化到-145 με,底面混凝土應變由28 με變化到-39 με;在同級預加力作用下,隨著豎向荷載的增大,混凝土頂面和底面的應變值也不斷的增大。

圖6 試驗梁頂面鋼筋應變—預加力曲線圖

圖7 試驗梁底面鋼筋應變—預加力曲線圖
從圖3和圖4中可以看出:在各級豎向荷載作用下,試驗梁頂面鋼筋和底面鋼筋實測應變值、公式計算應變值與有限元計算應變值相差很小,三者相符;在同級豎向荷載作用下,隨著預加力的增加,試驗梁頂面鋼筋的壓應變不斷增大,表現為線性變化,試驗梁底面鋼筋的應變由拉應變轉變為壓應變,變化趨勢也表現為線性,例如當豎向荷載為8 kN時,預應力從30 kN增大到120 kN的過程中,頂面鋼筋應變由-50 με左右變化到-115 με左右,底面鋼筋應變由50 με左右變化到-10 με左右;在同級預加力作用下,隨著豎向荷載的增大,混凝土頂面和底面的應變值也不斷的增大。
4結論
(1)在各級荷載作用下,試驗梁的試驗實測值、有限元計算值和理論公式計算值三者相符。
(2)各級豎向荷載作用下,預加力的增加會導致試驗梁的變形和應力(應變)減小,表明預加力會使試驗梁剛度增加。
參考文獻:
[1]謝功元. 在役混凝土梁永存預應力試驗研究[D].長安大學,2004.
[2]賈艷敏,王佳偉,韓基剛. 預應力簡支鋼箱梁固有頻率影響因素分析[J].工程力學,2009,(S1):37-40.
[3]張冬久,孫全勝. 預應力對PC梁動靜剛度影響的試驗研究[J].低溫建筑技術,2013,(7):72-75.
收稿日期:2016-01-12
作者簡介:張冬久(1987-),男,吉林九臺人,碩士,從事建筑結構設計與研究。
中圖分類號:U442
文獻標識碼:C
文章編號:1008-3383(2016)05-0097-02

