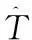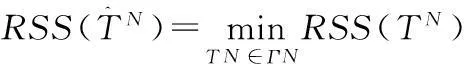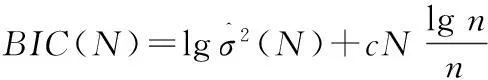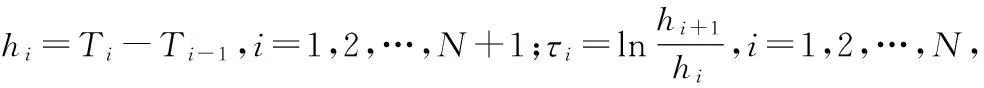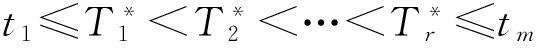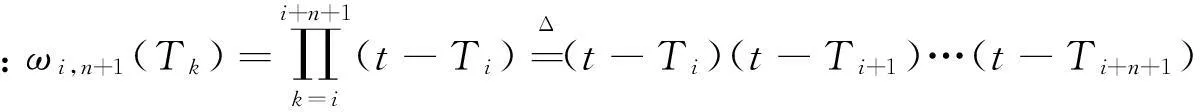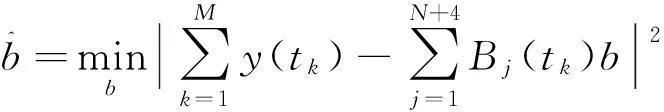相控陣雷達高采樣率數據事后處理方法研究*

曹淑艷，陳琦

(1.中國人民解放軍92941部隊，遼寧 葫蘆島　125000； 2.北京理工大學 信息與電子學院，北京　100081)

?

探測跟蹤技術

相控陣雷達高采樣率數據事后處理方法研究*

曹淑艷1，陳琦2

(1.中國人民解放軍92941部隊，遼寧 葫蘆島125000； 2.北京理工大學 信息與電子學院，北京100081)

摘要：針對相控陣雷達高采樣率數據，建立了雷達測量數據重采樣的最優節點樣條表示方法模型.為滿足試驗數據處理需求，進行擬合采樣的同時用迭代方法將野值剔除，有效地降低了雷達測量誤差。采用B樣條作為數值逼近的基函數，可在全部數據范圍內對測量數據進行擬合，達到提高處理精度的效果。通過仿真與實測數據的檢驗，驗證方法的正確性和實用性。

關鍵詞：相控陣雷達；B樣條；擬合；數值逼近；重采樣； 數據處理

0引言

外場試驗中，相控陣雷達通常以20 BZ的頻率來實時跟蹤測量飛行器的軌跡，并采集和記錄其測量數據，供事后分析處理。與實時輸出20 BZ的雷達測量數據相比，事后用高采樣率對雷達記錄數據進行重采樣能夠獲取更多的目標運動細節信息，提高數據處理精度，有利于對雷達測量誤差進行修正和抑制。另外，雷達測量數據的采樣時間和采樣頻率與其他測量設備很難統一，數據分析時也需要對雷達測量數據進行時間對齊，也就是對雷達測量數據擬合重新采樣。

在對雷達跟蹤飛行器測量數據處理時，目前多采用多項式擬合，但會帶來較大截斷誤差[1-2]；若用分段多項式擬合，不僅段落劃分比較費時，而且分段多項式銜接處出現拐點，嚴重影響了軌跡的光滑性與完整性。本文通過采用B樣條擬合平滑方法，研究適當的平滑區間長度和多項式階數，并采用B樣條作為數值逼近的基函數，可在全部數據范圍內對測量數據進行高精度擬合。通過對擬合的飛行器軌跡進行重采樣仿真分析，并與GPS真值比對，表明該方法對雷達測量誤差的抑制有較明顯的效果。

1高采樣率測量數據處理方法研究

針對常規測量數據處理中采用的最小二乘算法，對于含有修正殘差的海上環境雷達測量數據，多項式的截斷誤差較大，由此導致處理的綜合誤差增大。而采用自由節點樣條函數方法，通過合理的選擇節點，可以有效地分離出測量數據中的誤差，同時具有截斷誤差小的特點[3-5]。

通過大量試驗數據分析發現，影響樣條函數處理效果的一個關鍵因素是節點的選取。首先，節點不能選擇在噪聲和修正殘差較大的點上；其次，以含噪信號的特征點作為樣條函數節點，能夠達到較好精度。因此，在樣條函數處理前，先對雷達測量數據作預處理，排除誤差較大點的同時找出信號的主要特征點，以此作為樣條函數節點的參考點。采用BIC準則對擬合殘差與參數個數之間進行不同的權衡，以體現對殘差與階數二者重要性的不同側重。同時還可對測量數據采用觀察法，人工選取節點數，這一工程處理方法的特點是速度快，利于快速處理。本文基于對雷達測量數據擬合的重采樣處理，有效地抑制了測量誤差。

1.1基于B樣條函數的最小二乘擬合法

樣條函數是有限元理論中解決逼近問題的有效手段，它本身有諸多優良性[6]，因此，采用B樣條作為數值逼近的基函數，可在全部數據范圍內對測量數據進行高精度擬合，從而達到高精度平滑效果。

在最優節點樣條擬合前，需要初步確定雷達測量數據所用的節點數。可采用BIC準則或觀察法，確定樣條擬合節點數。

考慮模型：y(t)=P(t)+e(t)其中y(t)為初始雷達測量的軌跡數據，P(t)為真實軌跡數據，e(t)為隨機誤差。

設y(t)具有N次樣條多項式特征，并在m個時刻有采樣數據{y(ti),i=1,2,…,m}，a≤ti≤b．可獲得一個離散數據模型：

(1)

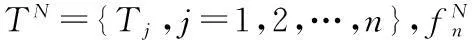
α=(α0,α1,α2,…,αn+N)T，

Y=(y(t1),y(t2),…,y(tm))T，

e=(e(t1),e(t2),…,e(tm))T，

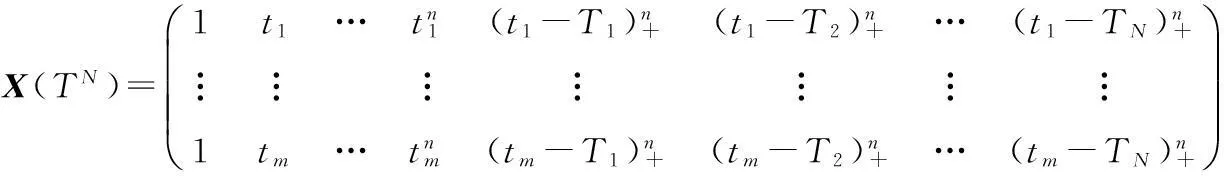
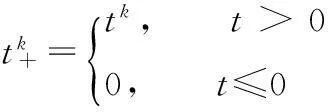
Y=X(TN)α+e.

(2)

模型(2)的參數估計可歸為如下非線性優化問題: 即求參數α,TN，使得問題

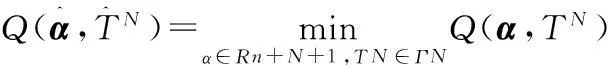
(3)

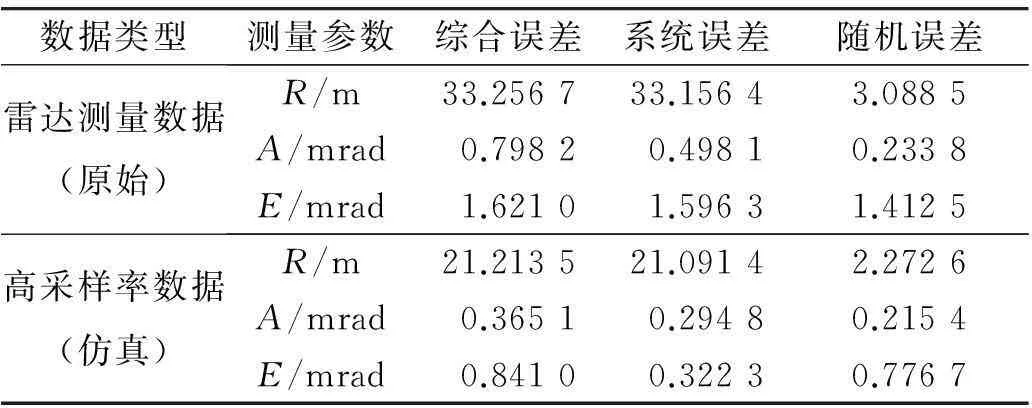
式中：ΓN={TN=(T1,T2,…，TN):a

(4)

式中:RSS(TN)=‖H(TN)Y‖2=YTH(TN)Y， H(TN)=I-P(TN)，這里I是單位陣。

P(TN)=X(TN)[X(TN)TX(TN)]-1X(TN)T.

(5)

為定量地給出P(t)(信號)與ε(t)(誤差)的分頻界線，對下述BIC量進行分析：

(6)

由以上理論，可以構造出下面的分頻算法：

Step 1： 給定N=L1，λ>0,δ>0及L2(L1≤L2)；

Step 2：IFN>L2GOTOStep 7；n=0，給定初始節點TN(0)(實際中，可由等距樣條節點提供) ;

Step 3：計算▽RSS(τN(n)),τN(n);

Step 4：計算τN=τN(n)-λ▽RSS(τN(n))/‖▽RSS(τN(n))‖；

IFRSS(τN)>RSS(τN(n)),λ=λ/2, GOTO Step 4;

IFRSS(τN)

Step 6：RSS(N)=RSS(τN(n)), 令N=N+1，GOTO Step 2;

Step 7：計算BIC(N)，確定N=L1,…,L2,L中的BIC(N)的雙極點N*，N**，即得到此段所對應的內節點數。算法中λ為收斂因子，δ為控制因子，L為最大樣條節點數。

用不等距節點標準B樣條擬合并返回每段的最小的BIC值對應的內節點數，算例對某一雷達跟蹤某飛行器的一次試驗數據計算結果如表1及圖1所示(圖中所示的值是無量綱的)，分析可得N*，N**分別為2和17。

圖1　內節點數N及BIC(N)值圖Fig.1　Inner node number N and BIC (N) value

1.2不等距節點樣條擬合

采用四階三次不等距B樣條基，根據樣條節點和樣條階數估計待擬合數據的樣條表示系數[10]。

考慮t1,t2,…,tm時刻的軌跡的表示問題，

T-3

第i個四階B樣條函數為

表1　由BIC準則來確定的節點數N及BIC值

(7)

(8)

則數據可表示為

(9)

樣條系數bj的估計值為

(10)

最優節點的確定步驟，具體算法如下：

Step 1：確定擬合樣條的階次；

Step 2: 確定擬合彈道的特征點；(允許為0)

Step 3：給定擬合樣條節點的個數；(內節點允許為0)

Step 4: 給定初始節點；(實際中在各時間段內由等距樣條節點提供)

若不滿意，可修改step 2和step 3中的初始條件重新進行計算。

1.3樣條節點和系數產生彈道參數

由得到的雷達測量飛行器初始軌跡參數的最優節點個數及最優節點序列，產生重采樣的飛行器軌跡參數。

Step 1: 讀取軌跡參數的節點；

Step 2: 對應于各個采樣時刻t, 計算4階3次不等距B樣條及其一階導數和二階導數；

Step 3: 計算各個采樣點的估計值；

Step 4: 按需要的采樣率輸出雷達數據。

2應用效果分析

應用本文的算法，對2次試驗的雷達分別跟蹤不同速度飛行器軌跡實測數據進行了仿真，并與GPS真值數據進行比對分析，如表2，3和圖2，3所示。可以看出，通過對雷達測量數據采用B樣條作為數值逼近的基函數進行擬合高采樣率重采樣處理[11-12]，有效地抑制了測量誤差，軌跡更加光滑。

表2　跟蹤某慢速目標仿真數據與GPS真值的比對結果

表3　跟蹤某亞音速目標仿真數據與GPS真值的比對結果

圖2　雷達測量數據與GPS一次差曲線圖Fig.2　First difference between Radar measuring data and GPS value

圖3　高采樣率重采樣與GPS數據的一次差比較圖Fig.3　First difference between resampling at high-sampling data and GPS value

3結束語

針對相控陣雷達采集、記錄飛行器軌跡測量數據的特性，研究的高采樣率數據處理方法，并利用實測數據進行了驗證[13-15]。通過對雷達跟蹤的飛行器軌跡數據進行高采樣仿真分析，并與GPS真值比對，對雷達測量誤差的抑制有較為明顯的效果。結果表明，利用高采樣率所獲得的目標運動細節信息，可提高數據處理精度，驗證了所提出方法的有效性。

參考文獻：

[1]羅海銀．導彈航天測控通信技術詞典[M].北京:國防工業出版社,2001.

LUO Hai-yin. Dictionary of Guided Missile、 Space、 Measure and Control、 Communication Technology[M].Beijing: National Defense Industry Press,2001.

[2]祝轉民，楊宜康.樣條函數最小二乘擬合的遞推計算[J].中國空間科學技術，2002(1)：31-33.

ZHU Zhuan-min, YANG Yi-kang. Extrapolation Calculate of Spline Function Least Square Fitting Method [J].China Space Science Technology, 2002(1) ：31-33.

[3]王永德,王軍.隨機信號分析基礎[M].北京：電子工業出版社，2009.

WANG Yong-de, WANG Jun. Analyze Foundation of Random Signal [M].Electronic Industry Press, 2009.

[4]劉利生，張玉祥.外彈道測量數據處理[M].北京：國防工業出版社，2002.

LIU li-sheng, ZHANG Yu-xiang. Data Processing of Exterior Ballistic Measurement [M].Beijing: National Defense Industry Press, 2002.

[5]楊位欽，顧嵐.時間序列分析與動態數據建模[M].北京工業學院出版社，1987.

YANG Wei-qin, GU Lan. Analysis of Time Sequence and Dynamic Data Modeling [M].Beijing Industry College Press, 1987.

[6]崔錦泰.多元樣條理論及其應用[M].西安：西安交通大學出版社，1985.

CUI Jin-tai.Multi- Spline Theory and Application [M].Xi’an:Xi′an Jiaotong University Press, 1985

[7]張金槐.線性模型參數估計及其改進[M].北京：國防科技大學出版社，1996.

ZHANG Jin-huai. Parameter Estimating of Linear Model and Ameliorating [M].National University of Defense Technology, 1996.

[8]王正明,易東云.測量數據建模與參數估計[M].長沙：國防科技大學出版社，1996.

WANG Zheng-ming, YI Dong-yun. Measure Data Modeling and Parameter Estimating [M].National University of Defense Technology, 1996.

[9]BAR-SHALOM Y, FORTMAN T E. Tracking and Data Associantion[M].New York: Academic Press,1988.

[10]王正明,易東云.彈道跟蹤數據的校準與評估[M].長沙：國防科技大學出版社，1999.

WANG Zheng-ming, YI dong-yun.Calibrating and Evaluating on Trajectory Tracking Data[M].Beijing: National University of Defense Technology, 1999.

[11]蔡慶宇，薛毅.相控陣雷達數據處理及仿真技術[M].北京：國防工業出版社，1997.

CAI Qing-yu, XUE Yi.Data Processing of Phased-Array Instrumentation Radar and Emulation Technology[M]. Beijing: National Defense Industry Press,1997.

[12]劉利生，白堤.測量系統的系統誤差主成分估計方法[J].宇航學報，1986(2)：1-9.

LIU Li-sheng,BAI Di.Principal Component Estimating Method of System Error for Measure System[J].Journal of Astronautics,1986(2):1-9.

[13]王省富.樣條函數及其應用[M].西安：西北工業大學出版社，1989.

WANG Xing-fu. Spline Function and Application[M].Xi′an:XinBei Industry University Press, 1989.

[14]WANG Zheng-ming, ZHU Ju-bo. Reduced Parameter Model on Trajectory Tracking Data with Applications [J]. Science in China (Series E), 1999(2):190-199.

[15]張守信．外彈道測量與衛星軌道測量基礎[M].北京:國防工業出版社,1992.

ZHANG Shou-xin. Base on Exterior Ballistic Measurement and Intersatellite Measurement [M]. Beijing: National Defense Industry Press, 1992.

Post-Processing Method for High-Sampling Rate Data of Phased Array Radar

CAO Shu-yan1，CHEN Qi2

(1.PLA，No.92941 Troop， Liaoning Huludao 125000,China;2.Beijing Institute of Technology,Information and Electronics college,Beijing 100081,China)

Abstract:Aiming at high-sampling data of phased array radar, an optimal node spline representation method is developed for radar measuring data resampling. To meet the needs of test data processing, the processed method could fit the samplings while eliminating the outliers, which may effectively reduce the radar measuring error. B-spline is employed as the basis function for numerical approximations, which makes the full-data-scale fixing of measuring data possible so that a high-precision may be achieved. The validity and practicability are verified.

Key words:phased array radar; B-spline; data fit; numerical approximations; resampling；data processing

*收稿日期：2015-09-09；修回日期：2015-12-21

作者簡介：曹淑艷(1968-)，女，黑龍江密山人。高工，碩士，主要研究方向為數據處理與系統評估。

通信地址：125000遼寧葫蘆島市海濱南路1號E-mail：caoshuyan_ch@163.com

doi:10.3969/j.issn.1009-086x.2016.02.020

中圖分類號：TN958.92；TP391.9

文獻標志碼：A

文章編號：1009-086X(2016)-02-0119-05