南極洲地表平均溫度的定量分析

朱家明，高非含 ，陳嘯遠，印芷水

(安徽財經大學 統計與應用數學學院，安徽 蚌埠 233030)

?

南極洲地表平均溫度的定量分析

朱家明，高非含 ，陳嘯遠，印芷水

(安徽財經大學 統計與應用數學學院，安徽 蚌埠 233030)

摘要：針對如何定義并評估區域平均地表溫度的問題，使用了MATLAB、EXCEL等軟件，分別建立極限區域平均地表溫度模型、三維插值模型和多項式擬合模型，從而得出了南極洲從2001—2015年平均地表溫度值以及其與時間的函數關系式。緊接著根據得出的溫度與時間的關系對未來近5年進行了預測，以便更好地掌控未來溫度信息，做出及時的應對措施。

關鍵詞：南極洲；地表平均溫度；氣候變暖

0引言

有專家測算南極洲近15年的平均地表溫度有下降趨勢的結論[1]。緊接著還對南極洲未來近5年的平均地表溫度進行簡單預測，以便更好地掌控未來溫度信息，本文旨在尋找南極洲地表平均溫度的趨勢來估計全球是否變暖并建立了區域極限平均地表溫度模型(詳見2015年小美賽數學建模B題)。

1地表溫度的評價結果

1.1研究思路

我們建立了三維插值模型對新定義的平均地表溫度進行求解，得出了南極洲從2001—2015年間的平均地表溫度值定義并評估平均地表溫度。依據理想平均地表溫度計算公式，并結合極限思想建立了連續離散化地表溫度模型，對平均地表溫度進行了新的定義。緊接著，我們建立了三維插值模型對新定義的平均地表溫度進行求解，得出了南極洲從2001—2015年間的平均地表溫度值，建模流程如圖1。

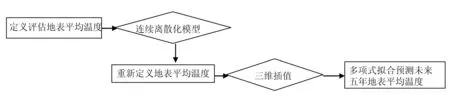
圖1　求解平均地表溫度思路流程圖

1.2數據處理

據英國南極調查網站整理的數據，理想化的情況下可將區域地表平均溫度積分并與面積作比，而在實際計算中,一定區域內的溫度一般由若干個觀測點得到的離散數據，不是一個連續函數, 所以我們建立連續離散化模型，通過三維插值進行求解。

為更好地對南極洲所在區域有限的考察站的溫度數據進行樣條插值，需要對南極洲進行直角坐標系的建立，并對各南極考察站進行坐標表示。在此過程中我們打算將球面上的南極洲視為平面。通過網絡搜集南極洲的平面地圖，建立平面直角坐標系，見下圖2所示。

圖2　南極洲考察站示意圖

利用軟件電子尺對圖2中的各個考察站在平面直角坐標系的位置進行測量得到它們的坐標數據，并結合圖中所給的比例尺進行實際距離的換算，測量結果和換算結果見下表1所示。

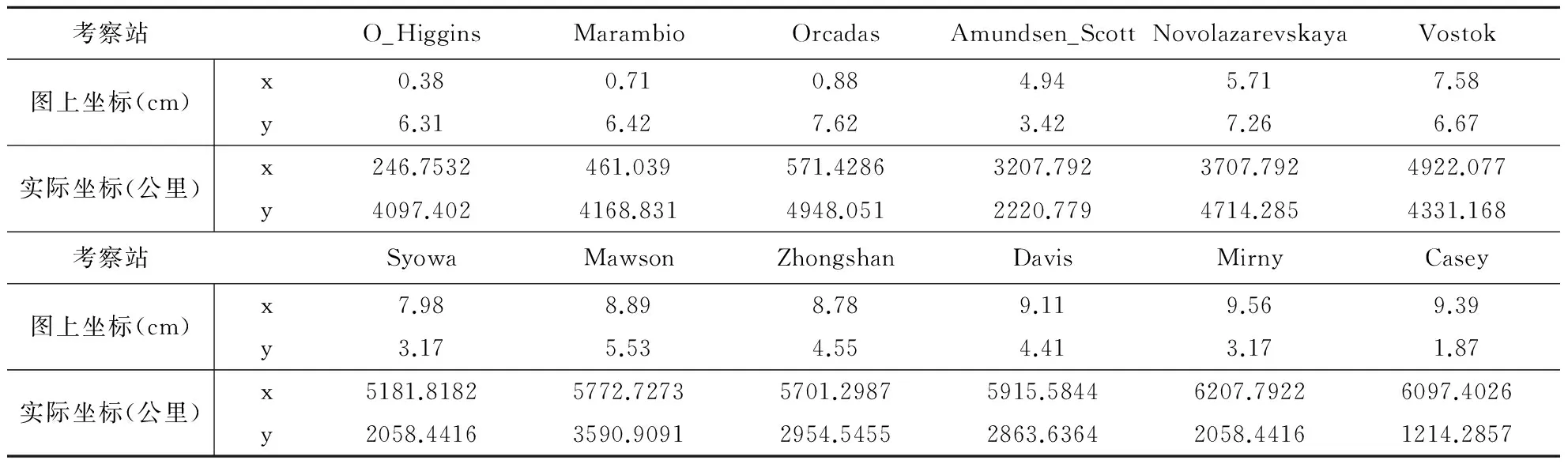
表1　考察站位置坐標數據

結合表1中的實際坐標數據，運用MATLAB軟件對坐標平面內的各個考察站進行標示，標示結果見下圖3所示。

圖3　各個考察站坐標標示

2極限區域地表平均溫度模型

2.1研究思路

據英國南極調查網站整理的數據，理想化的情況下可將區域地表平均溫度積分并與面積作比，而在實際計算中，一定區域內的溫度一般是由若干個觀測點得到的離散數據，不是一個連續函數, 所以我們建立極限區域平均溫度模型，通過三維插值進行求解。

2.2模型建立

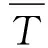
(1)

在實際計算中區域Φ內的溫度一般是由若干個觀測點得到的離散數據，不是一個連續函數，區域Φ的溫度不能都由觀測點體現，因此區域Φ內的理想平均溫度不可因此求得。

對于離散的觀測點數據，如果觀測點的數量很多，有i個。當i趨于無窮大時，那么對Φ內的i個觀測點的溫度T(r，t)進行加總并與區域Φ的面積S作比值，就得到了該區域Φ的平均溫度計算公式：

(2)

由于觀測點i是無窮大的，可理解成區域內每個觀測點所占的面積是無窮小的。設△Ti(t) 為面積大小為△的第i個觀測點的溫度，當面積△趨于無窮小時，將區域Φ內的i個觀測點的溫度進行加總并與區域Φ的面積作比值，就得到了該區域Φ的平均地表溫度計算公式：

(3)

3三維插值模型

3.1研究思路

針對上述區域Φ的平均溫度求解公式(3)，我們知道需要盡可能多的觀測點數據，這樣才能使每個觀測點所占的面積盡可能地小。在現實生活中對某個區域各個觀測點的數據采集量是有限的，遠遠無法用于公式(3)來對該地區的平均溫度進行計算。現在需要通過區域內有限個觀測點地表溫度數據得到區域內盡可能多的地表溫度數據。我們可以利用軟件MATLAB對該區域已有的有限個觀測點的的數據進行三維插值[3]，建立三維插值模型，進而得到該區域內足夠多的數據。

3.2模型建立

通過使插值點間斷盡可能小的方法進行插值，這樣就能得到該區域內極小面積內所對應的地表溫度值。假設有N個極小區域面積所對應的地表溫度數據，記作△Ti(t)。從而就可以對這N個極小區域面積所對應的地表溫度數據△Ti(t)進行加總并與區域面積作比值，這樣便得到了新的區域平均溫度估算公式：

(4)

公式(4)中的N是通過設置極小間斷進行三維插值得到的區域觀測點數量，是個很大的數量。這樣在允許的誤差范圍內，公式(4)就能對公式(3)進行數值上的估算。

3.3模型求解結果

2001—2003年插值結果見下圖4所示。

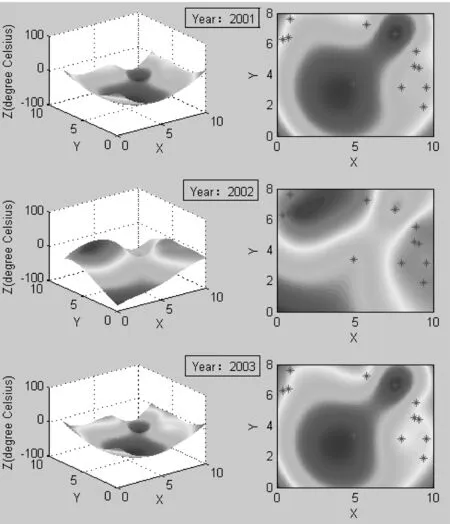
圖4　2001-2003年地表平均溫度插值結果

在上述圖4中，左側的三維曲面表示區域溫度的起伏狀況，右側是三維地表溫度的俯視圖像，其中的‘*’表示南極洲上的各個考察站。在圖中，冷色區域代表的地表溫度要低于暖色區域所代表的地表溫度，從而可以看出南極洲的平均地表溫度有高有低，存在著較大的地理區域差異性。

同樣，做出2004—2015年南極洲平均地表溫度的三維插值圖，見下圖5～圖8所示。

圖7　2010—2012地表平均溫度插值結果　　圖8　2013—2015地表平均溫度插值結果

4多項式擬合模型

4.1研究思路

要描述南極地區地表溫度和時間之間的情況,首先需要對從2001—2015年南極地區的地表溫度進行分析，找出地表溫度與年份之間的關系。

運用軟件MATLAB表1據進行散點圖繪畫，年份與平均地表溫度間的散點關系見下圖9所示。

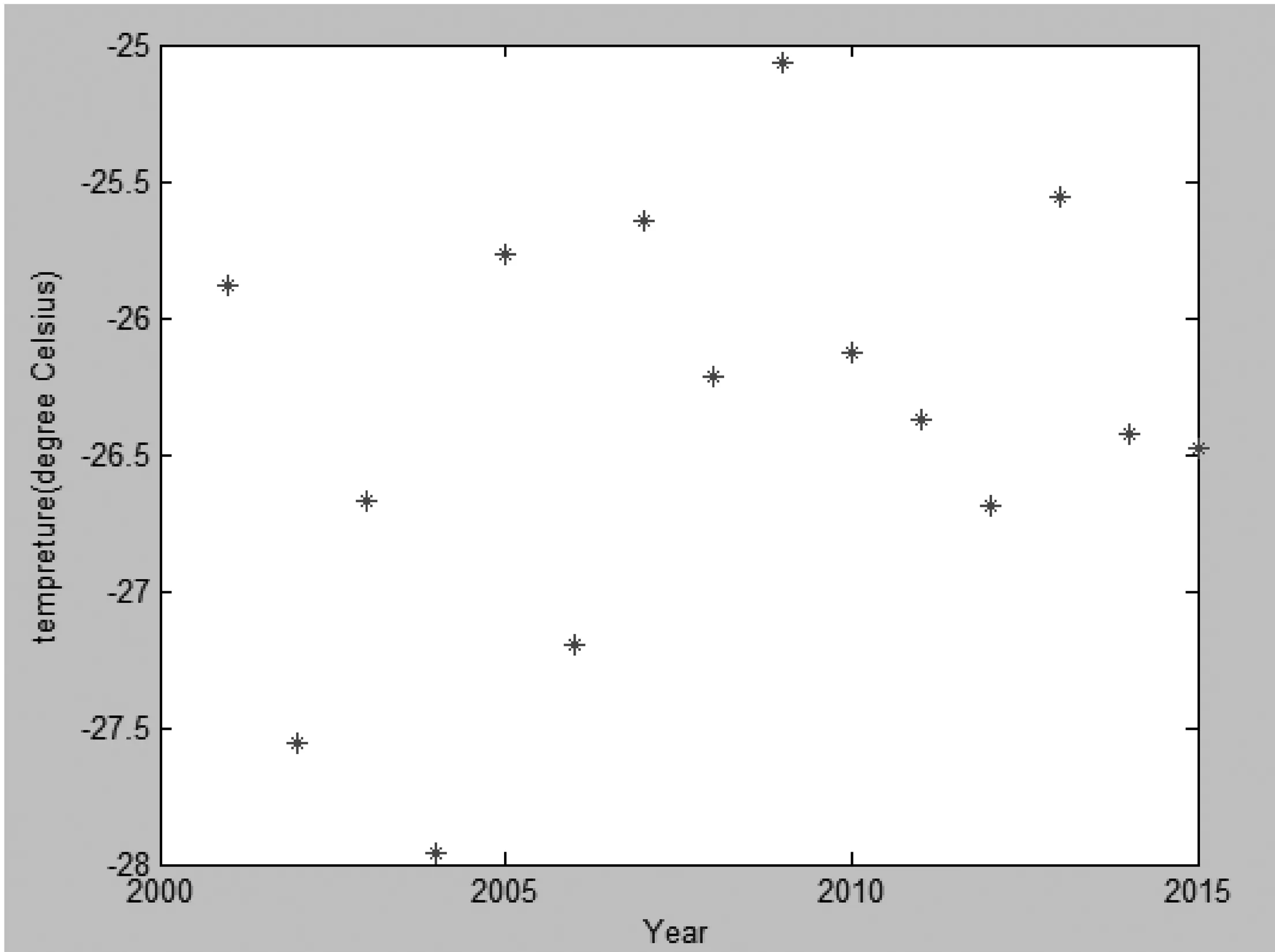
圖9　年份與平均地表溫度間的散點關系

通過上圖發現時間與地表溫度間大致呈現出多項式函數關系，所以可對散點之間進行多項式擬合。以(年份-2000)為自變量X，地表溫度為因變量Y分別進行一至四次多項式擬合：

一次多項式擬合：Y1=ax+b

(5)

二次多項式擬合：Y2=a2x2+a1x+b

(6)

三次多項式擬合：Y3=a3x3+a2x2+a1x+b

(7)

四次多項式擬合：Y3=a4x4+a3x3+a2x2+a1x+b

(8)

為了能夠更好地反映地表溫度與時間之間的關系，應對上述多項式進行誤差計算。設時間所對應的真實地表溫度值為Y，根據擬合出來的多項式計算出來的地表溫度值為Yi(i=1，2，3，4)。計算真實值與計算值間的離差平方和，選取離差平方和最小所對應的多項式。其中，離差平方和計算公式為：

(9)

運用軟件MATLAB對表1的數據分別進行一至四次多項式擬合，擬合結果和各自的離差平方和見下表2所示。

表2　擬合結果和各自的離差平方和

由上表可以看出三次多項式和四次多項式的離差平方和都比較小，下面運用軟件MATLAB畫出二者和實際數據的圖像，見下圖10所示。

圖10　擬合圖

雖然四次多項式的離差平方和小于三次多項式離差平方和，但是從上述圖中可以看出，四次多項式的最終趨勢是上升的，在未來的近幾年會達到很高的溫度，這不符合南極地區未來的地表氣溫狀況，故舍去四次多項式，最終選擇三次多項式作為2001—2015年間南極地表溫度和時間之間關系表達式。

y3=-0.0038x3+0.830x2-0.4120x-26.2556

(10)

通過上述公式(10)，可以簡單地對南極洲未來幾年的地表平均溫度進行預測。取P液，可以得到未來2016年、2017年、2018年、2019年和2020年南極洲的平均地表溫度。計算結果見下表3所示。

表3　2016年～2020年預測溫度

表3的結果反映了南極洲未來5年的平均地表溫度呈現下降的趨勢，由此可以分析：全球變暖的現象日趨嚴重，該結論正與全球變暖引起極地冰雪融化并吸收熱量，從而導致地表平均溫度逐年下降的物理現象相吻合。

5結語

我們建立了三維插值模型，通過設置極小間斷進行三維插值得到的區域觀測點數量，是個很大的數量。這樣在允許的誤差范圍內，進行數值上的估算。這近15年南極洲平均地表溫度大致在-25攝氏度～-27攝氏度范圍內，且呈現下降趨勢。最后建立了多項式擬合模型，對南極洲平均地表溫度和時間之間的關系進行了分析，得出未來近5年南極平均地表溫度也有下降趨勢的結論。

[參考文獻]

[1] 楊保，史鋒，Sonechkin D M,等.過去千年氣候變化重建研究新進展[J].中國沙漠，2011，3(2):485-491.

[2] 張曉峒.計量經濟學基礎.3版[M].天津：南開大學出版社，2007.

[3] 唐國利，王邵武，聞新宇，等.全球平均溫度序列的比較[J].氣候變化研究進展，2011，7(2):85-89.

[4] 茆詩松，程依明，濮曉龍.概率論與數理統計教程.2版[M].北京：高等教育出版社，2011.

[責任編輯：崔海瑛]

作者簡介：朱家明(1973-)，男，安徽泗縣人，副教授，數學建模實驗室主任，從事應用數學與數學建模研究。

基金項目：國家級大學生創新創業項目(201410378192)；國家自然科學基金項目(11301001)；安徽財經大學教研項目(acjyzd201429)。

中圖分類號：O119

文獻標識碼：A

文章編號：2095-0063(2016)03-0009-05

收稿日期：2015-12-24

DOI 10.13356/j.cnki.jdnu.2095-0063.2016.03.003