基于非線性彈簧的三排圓柱滾子組合轉盤軸承靜態承載能力模型
姬麗麗,王華,潘裕斌,韓云科
(南京工業大學,南京 210009)
三排圓柱滾子組合轉盤軸承廣泛應用于起重機、挖掘機等領域[1],鑒于其結構、受載、滾道力學性能的復雜性等,傳統圓柱滾子軸承的動、靜態承載能力計算方法并不適用[2-5]。基于有限元的數值法是目前復雜結構計算的主要方法,但三排圓柱滾子組合轉盤軸承中圓柱滾子/滾道接觸數目多且為非線性,直接建立實體模型進行計算時計算量大,甚至不收斂。文獻[6-7]提出了一種新穎且簡單的計算模型用來計算在單排圓柱滾子轉盤軸承中實際受載的圓柱滾子數目,但假設轉盤軸承僅承受徑向力。文獻[8]用非線性桁架單元代替三排圓柱滾子組合轉盤軸承中的圓柱滾子,研究圓柱滾子的尺寸及修形系數對圓柱滾子載荷-變形特性的影響,但只建立了1/8單個圓柱滾子與局部滾道接觸模型。文獻[9]通過比較與內圈接觸的圓柱滾子上的最大內部載荷和轉盤軸承軸向承載能力來確定外部載荷,求出三排圓柱滾子組合轉盤軸承靜態承載能力曲線,并且采用非線性桁架單元,研究螺栓數目和預緊力對轉盤軸承承載能力的影響[10]。運用非線性桁架建模時通常只建立單圓柱滾子/滾道局部接觸模型,文獻[11-12]提出采用非線性彈簧代替滾子,并基于Hertz接觸理論獲得非線性彈簧的剛度曲線,然后用于建立單排、雙排球轉盤軸承的計算模型,研究其載荷分布情況和承載能力,提高了計算效率。
文中以131.32.940Z型三排圓柱滾子組合轉盤軸承為研究對象,采用非線性彈簧模擬圓柱滾子,建立轉盤軸承模型進行仿真計算,提高了圓柱滾子/滾道非線性接觸的計算效率,探討外載荷作用下轉盤軸承內部接觸載荷的分布情況,為設計和加工提供參考。
1 非線性彈簧模擬圓柱滾子
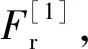
分析流程如圖2所示,首先分別求出上排和下排中最先失效的圓柱滾子所承受的最大接觸載荷,作為單個圓柱滾子接觸模擬的外載荷。然后基于有限元接觸模型的數值法計算獲取單個圓柱滾子僅承受沿圓柱滾子徑向方向外載荷時的載荷-變形曲線,并通過單圓柱滾子徑向壓縮試驗驗證,最后將其作為三排圓柱滾子組合轉盤軸承整體模型中非線性彈簧剛度曲線,進行轉盤軸承內部接觸載荷分布和整體變形分析。
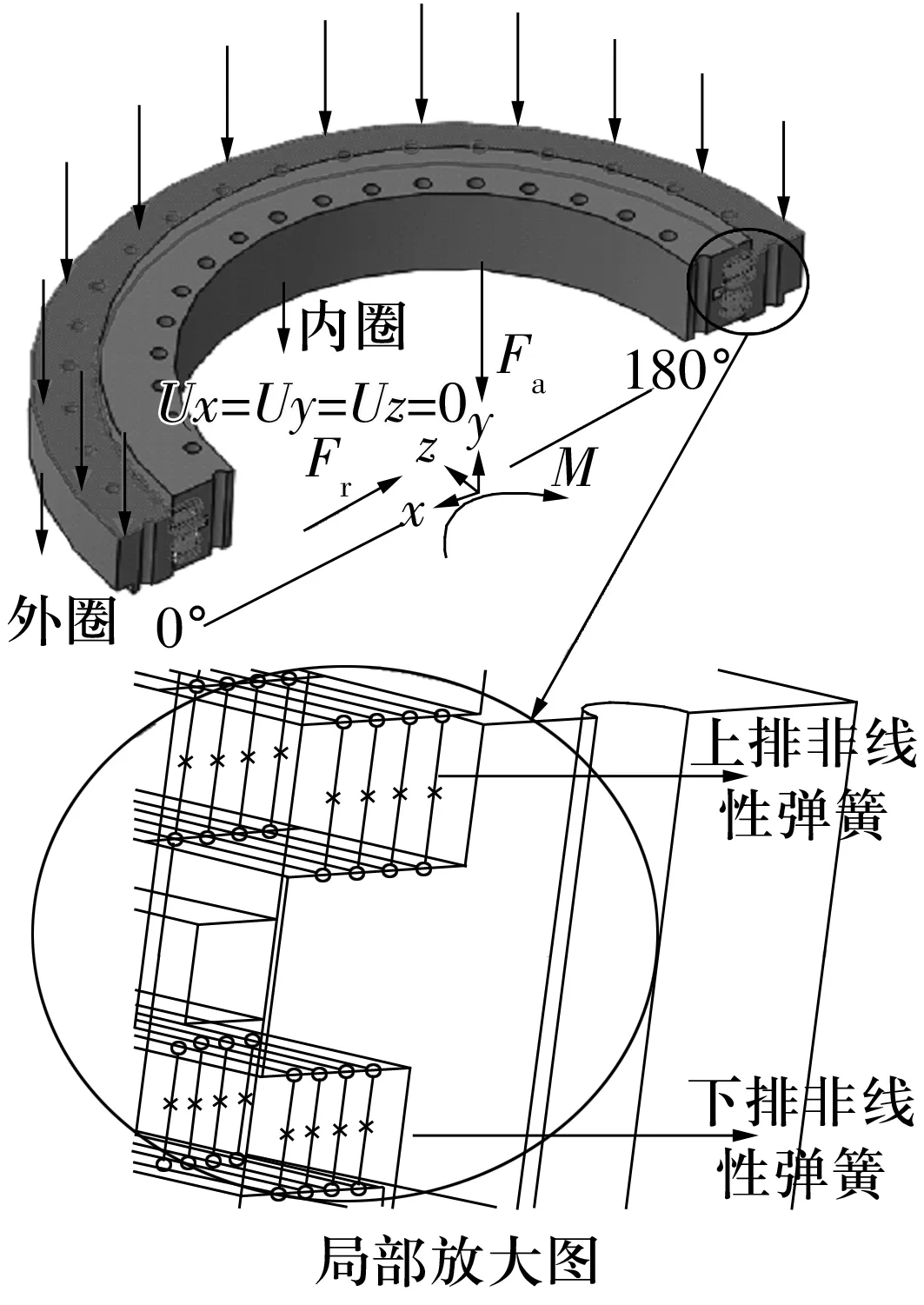
圖1 轉盤軸承受載情況

圖2 分析流程圖
2 非線性彈簧剛度計算方法及驗證
非線性彈簧模擬圓柱滾子的關鍵是獲取彈簧的非線性剛度系數。文中采用數值法計算,并通過試驗驗證獲取單圓柱滾子/滾道接觸的載荷-變形曲線,即非線性彈簧的剛度系數曲線。分析時,為簡化模型,提高計算效率,忽略了圓柱滾子邊緣修形。
2.1 最大接觸載荷
圓柱滾子與滾道之間的最大接觸載荷[14]為
(1)
式中:Dpw為滾子組節圓直徑;Z為圓柱滾子個數; “+”表示上排圓柱滾子,“-”表示下排圓柱滾子。
131.32.940Z型三排圓柱滾子組合轉盤軸承部分結構參數見表1。
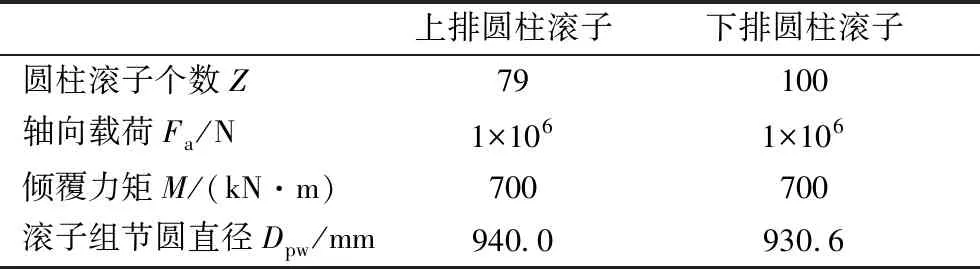
表1 轉盤軸承參數
上述數據代入(1)式得上排圓柱滾子和下排圓柱滾子的最大接觸載荷分別為25 kN和40 kN。
2.2 有限元分析
該轉盤軸承結構如圖3所示。套圈采用42CrMo,其強度高,疲勞極限高;圓柱滾子材料采用GCr15,具有良好的耐磨性、高的接觸疲勞性能。其材料參數見表2。
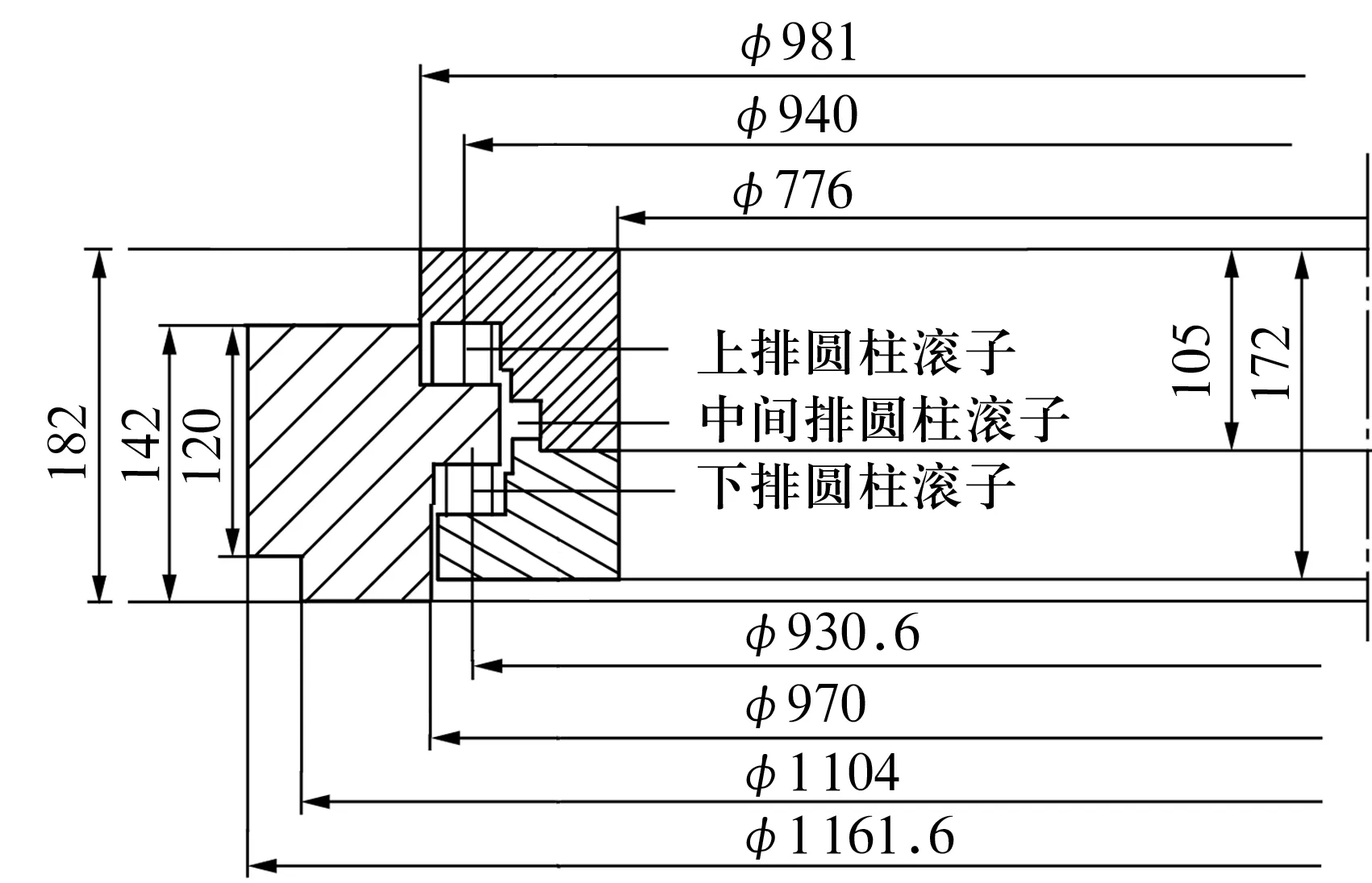
圖3 轉盤軸承結構簡圖及其相關尺寸
以上排圓柱滾子為例,建立圓柱滾子/滾道接觸副的彈塑性有限元模型,如圖4所示,施加的軸向載荷取最大接觸載荷25 kN,方向為沿x軸負方向,網格劃分的單元類型設置為C3D8R(8節點六面體線性縮減積分單元),在接觸區域進行局部細化,以提高計算效率且容易收斂。 按照實際情況在總體坐標系下完全約束下滾道上的6個自由度,釋放上滾道和圓柱滾子在x軸方向上的自由度。
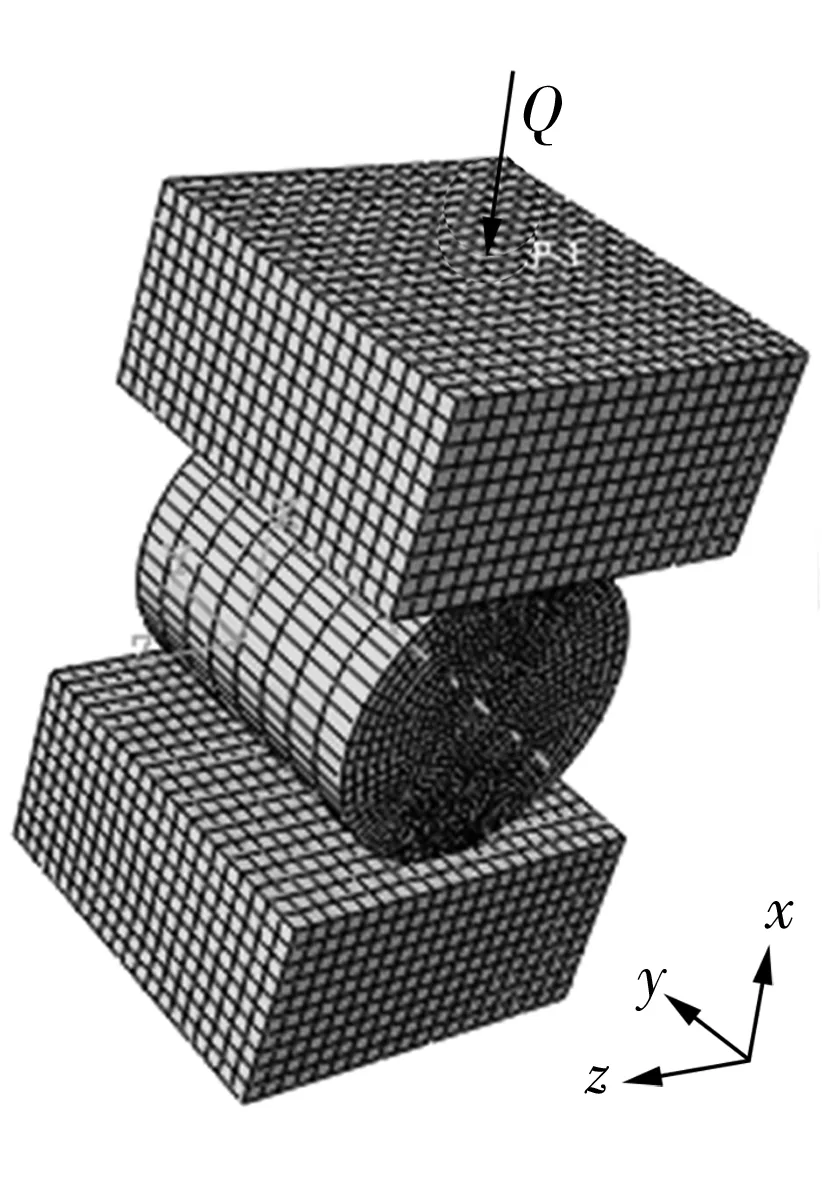
圖4 上排圓柱滾子/滾道接觸副
運行ABAQUS/Standard模塊,使用Newton-Raphson算法求解非線性問題,分析過程被劃分為一系列載荷增量步,所有增量步的響應之和為該非線性分析的近似解,有限元模型計算結果如圖5所示。由圖可知,上排圓柱滾子/滾道接觸模型的最大變形量為0.024 mm,圓柱滾子的最大總變形量為0.020 mm,圓柱滾子沿載荷作用方向的最大變形量為0.020 mm,仿真得到的載荷-變形曲線如圖6所示。同理可得下排圓柱滾子/滾道接觸模型的最大變形量為0.072 mm,圓柱滾子的最大變形量為0.059 mm,圓柱滾子沿載荷作用方向的最大變形量為0.059 mm,仿真得到的載荷-變形曲線如圖7所示。
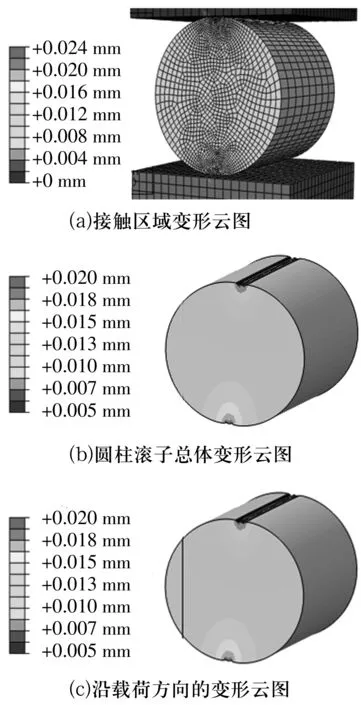
圖5 上排圓柱滾子/滾道接觸副
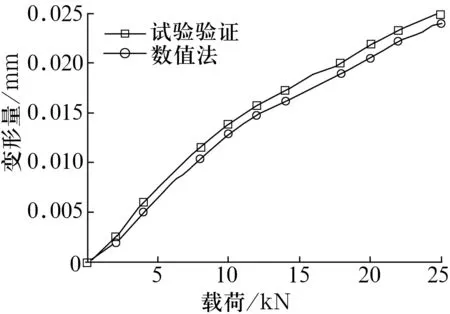
圖6 上排圓柱滾子載荷-變形曲線
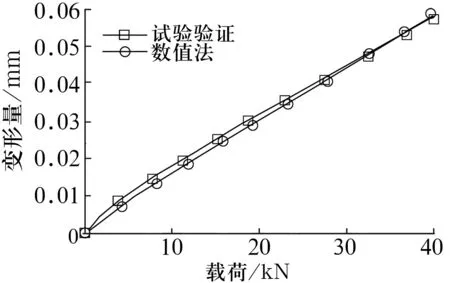
圖7 下排圓柱滾子載荷-變形曲線
輸出在分析步遞增過程中單個圓柱滾子上各個非線性彈簧上載荷和變形量的關系為[1]
,(2)
式中:di,m為圓柱滾子直徑;lt為相鄰非線性彈簧間距;δi,m為每個非線性彈簧變形量;i為圓柱滾子排索引號,1為上排,2為下排;m為單個圓柱滾子上非線性彈簧索引號。qz,j,m為圓柱滾子與內圈滾道之間的載荷在z軸上的分量。
2.3 試驗驗證
通過試驗對數值法所得圓柱滾子載荷-變形曲線進行驗證。試驗時,載荷和位移均獨立控制,疲勞壓縮試驗裝置的結構和圓柱滾子裝夾位置如圖8所示。用上下夾具夾緊固定圓柱滾子,其中下夾具與液壓伺服系統相連,載荷通過下端的液壓伺服系統施加在夾具上,電子千分表的觸點在下夾具上,圓柱滾子的變形量由千分表測量,上端內置載荷傳感器記錄加載的載荷值,并在電腦終端讀出。試驗最大加載為25 kN,將其按照等差數列分為10組,記錄每次加載值和對應的圓柱滾子沿載荷方向上的變形量,得到圓柱滾子載荷-變形曲線(圖6)。同理可得下排圓柱滾子的載荷-變形曲線(圖7)。

1—上夾頭;2—上夾具;3—上排圓柱滾子;4—下夾具;5—下夾頭;6—千分表;7—磁座
試驗結果表明,數值法與試驗法的趨勢相同,上排圓柱滾子的最大誤差點的數值法計算值和試驗值分別是0.020 4,0.021 9 mm,最大誤差為7%;下排圓柱滾子的最大誤差點的數值法計算值和試驗值分別是0.011 4,0.015 mm,最大誤差為7%,誤差較小,表明數值法所得載荷-變形曲線可直接用于計算轉盤軸承模型中非線性彈簧的剛度系數。
3 實例分析
在三排圓柱滾子組合轉盤軸承非線性彈簧有限元模型中添加數值法求得的非線性彈簧的載荷-變形數據,假設內外圈滾道為剛體,圓柱滾子為柔體,材料屬性見表2,在外圈施加沿y軸負方向軸向力和繞z軸的傾覆力矩,內圈自由度全約束,計算收斂,計算結果如圖9所示。

圖9 轉盤軸承的內部接觸載荷分布情況
由于模型網格劃分密度以及沒有考慮圓柱滾子/滾道接觸間隙等原因,有限元分析結果與理論計算所得的最大接觸載荷存在一定誤差,上排圓柱滾子的最大接觸載荷22 kN在0°位置,方向沿y軸負方向,理論計算值為25 kN,兩者相差12%,在81°~180°位置接觸載荷為0,圓柱滾子與滾道為非接觸狀態;對于下排圓柱滾子,最大接觸載荷41 kN在180°位置,方向沿y軸負方向,理論計算值為40 kN,兩者僅相差3%,在0°~72°位置接觸載荷為0,即圓柱滾子與滾道為非接觸狀態。
非線性彈簧模型的整體變形云圖和變形分布情況如圖10所示,最大變形量0.050 mm在180°位置,最小變形量0 mm在70°位置,0°位置的變形量為0.029 mm。
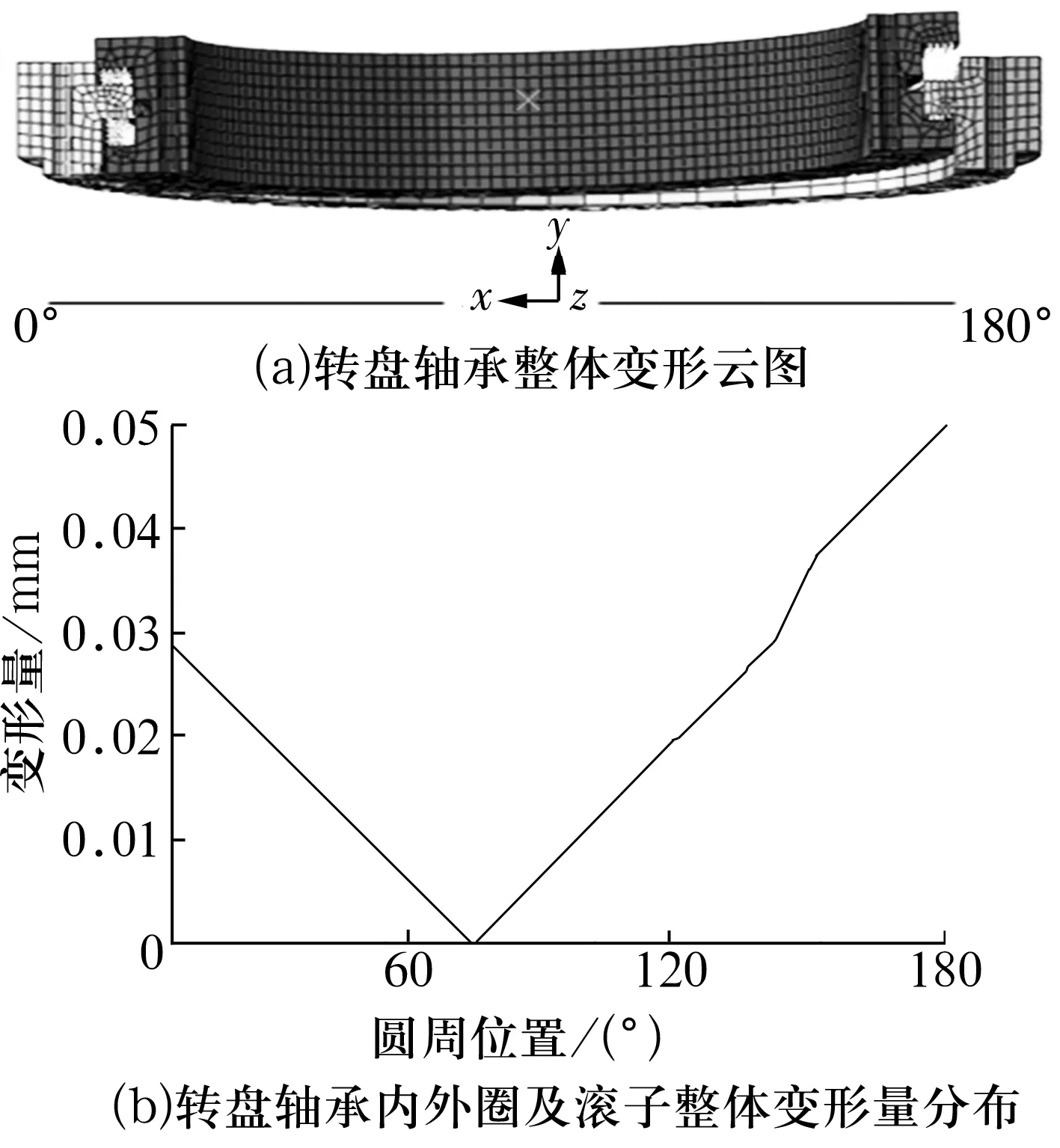
圖10 轉盤軸承變形量
當20個處理器并行時,通過監測模塊獲取的基于非線性彈簧的轉盤軸承載荷計算時間僅為 202 s,計算效率高,且易于收斂。
4 結論
1)通過數值法得到單個滾子/滾道接觸時載荷-變形曲線,并用試驗方法進行驗證,結果誤差小于7%,表明基于有限元數值方法所得載荷-變形曲線可以作為非線性彈簧剛度曲線,用于轉盤軸承的內部接觸載荷分布和轉盤軸承整體變形情況的分析計算。
2)基于非線性彈簧對三排圓柱滾子組合轉盤軸承進行計算,得到在軸向力和傾覆力矩共同作用下的內部接觸載荷分布曲線和轉盤軸承整體變形量分布情況,上、下兩排最大接觸載荷與理論計算結果基本一致,且計算時間短,因此用非線性彈簧代替圓柱滾子研究三排圓柱滾子組合轉盤軸承靜態承載能力滿足設計要求且高效。

