海洋剪切流下失穩內波流場及傳播的理論分析

鄧冰，張宇飛，朱娟，張銘

（1.北京應用氣象研究所，北京100029；2.中國海洋大學海洋環境學院，山東青島266003；3.解放軍61139部隊，北京100081；4.解放軍理工大學氣象海洋學院，江蘇南京211101）

海洋剪切流下失穩內波流場及傳播的理論分析

鄧冰1，張宇飛2，朱娟3，張銘4

（1.北京應用氣象研究所，北京100029；2.中國海洋大學海洋環境學院，山東青島266003；3.解放軍61139部隊，北京100081；4.解放軍理工大學氣象海洋學院，江蘇南京211101）

摘要：采用求解特征值的方法，探討了剪切背景流所導致的短波長海洋內波的失穩問題，并給出了其流場結構和傳播情況。按照失穩內波波陣面的法向與背景流流向夾角的不同，海洋內波不穩定可分為橫波不穩定（夾角為0°），對稱不穩定（夾角為90°）和斜交不穩定（任意夾角）3種情況，此時不穩定內波的流場呈現多種形態。對最不穩定流場而言，對稱不穩定的流場形態呈現單圈環流的傾斜對流形態，而橫波不穩定和斜交不穩定的流場形態則有貓眼結構出現。對于橫波不穩定和斜交不穩定內波，最不穩定內波與次不穩定內波兩者的流場分布幾乎互為鏡像。相應于本文的短波長內波，橫波不穩定和斜交不穩定的內波均為高頻內波，對稱不穩定內波不傳播，而僅在原地增長。相同參數下垂直方向結構最簡單的對稱不穩定內波其增長率最大。

關鍵詞：剪切流；失穩海洋內波；流場結構；傳播

1　　引言

海洋內波以約化重力為恢復力，本質是內重力慣性波，并屬海洋的中、小尺度系統。海洋內波目前受到了學者的廣泛重視［1-2］，它的存在使得海水運動以及水文要素的分布與變化更加復雜，在物理海洋學中必須要考慮其作用［3］。海洋內波動的發生、發展和演變一直是物理海洋學研究的重點和熱點［4-6］。從動力學角度分析海洋內波的失穩不僅可以豐富和深化內波理論，而且具有實際的應用價值。

研究表明，海洋剪切背景流會造成海洋內波的失穩［7-8］。在實際海洋中也發現了這樣的事實。范植松等［9］發現在渤海南部存在很強的周期約為6 min的次重力波，該次重力波具有內波的某些特性，推測其主要是由潮流的剪切不穩定所導致。Yuan等［10］分析了黑潮的不穩定性，提出了其可激發內波的機制，指出對于向西傳播的擾動，黑潮西翼流場是不穩定的，此時所導致的失穩內波的傳播方向向西；他們還解釋了衛星SAR圖像觀測到的內波與黑潮西邊界共存的現象，從而進一步驗證了以上機制。Rainville等［11］分析了中國海東部的黑潮海洋調查資料，發現黑潮中有較強剪切流；他們還分析了日本九州黑潮附近連續30 h的觀測資料，發現在黑潮中心的剪切流處，存在著向上、下傳播的高頻內波，并認為黑潮較強的剪切流是生成海洋內重力慣性波的重要因素。對剪切背景流導致內波失穩進行研究，可以了解內波產生和發展的條件，是內波研究的一個重要方面。利用標準模方法，將波動穩定性問題化為本征值的邊值問題，是解決流體穩定性問題的有效方法［12-13］。然而由于數值求解的困難，只有很少的幾種特殊情況可以解析求解該特征值問題。1990年，曾慶存等首次對正壓非地轉大氣中水平切變基本流下的大氣穩定性問題成功進行了數值求解［14-15］，之后張立鳳和張銘又將該數值求解方法引入具有垂

當前因海洋內波觀測資料的匱乏以及觀測精度的限制，很難精細觀測到內波流場的特征，這給考察失穩內波的流場結構帶來困難。為此在理論上求取失穩內波的流場結構也為解決以上困難提供了一條可行的途徑。我們在文獻［18］中提出了一個研究剪切背景流導致內波失穩的理論模型，并給出了內波的譜點分布及譜函數的垂直結構，但未給出失穩內波的流場結構。文獻［19］中，我們利用以上模型得到的特征值問題，給出了沿剪切背景流方向傳播的失穩長波長內波有關該問題的數值解，得到了其流場結構。然而失穩內波相對剪切背景流的傳播可以存在多個方向，并非只有沿著該背景流方向傳播，而且短波長內波是內波中重要的組成部分，其空間尺度小，振蕩頻率高，更難以獲取實測資料，因此對其進行理論分析就更顯必要；這種內波對潛艇航行影響更大，對其研究還有重要的應用價值。為了彌補文獻［18］和［19］的不足，本文仍利用以上模型，從理論角度考察了剪切背景流所導致的短波長海洋內波的失穩，并給出了相對背景流不同傳播方向的短波長失穩內波的流場結構和傳播情況。結果表明，這些失穩內波的流場結構彼此不同，沿背景流傳播的短波長失穩內波與文獻［19］中的長波長失穩內波的流場結構也有很大差別。

2　　數值模型和參數設計

本文采用無粘絕熱二維Boussinesq方程組［18］（可濾去聲波）考察海洋內波的失穩問題。該方程組中設海面和海底均是水平剛璧（不考慮海底地形），同時考慮了地球旋轉，取地轉參數 f為常數，并設海洋內波波陣面的法向為x方向，若內波傳播的話，則該方向也是內波的傳播方向。在此因取 f為常數，故x不必一定指向東，x的法向為y方向，這也是該內波波陣面的方向。通常內波狀態沿y方向的變化比沿x方向的變化要緩慢得多，故可近似認為內波沿y方向的狀態不變，這樣內波的各物理量在y方向的偏微商可近似看作0，這也是本文能采用二維Boussinesq方程組的原因。z方向由海底向上指向海面，并設海底z=0。在方程組中還引入了垂直方向流速具有切變而流向不變的剪切背景流U（z），其流向與x軸有一個交角δ，在x軸和y軸上的分量則分別是ū和（見圖1）。

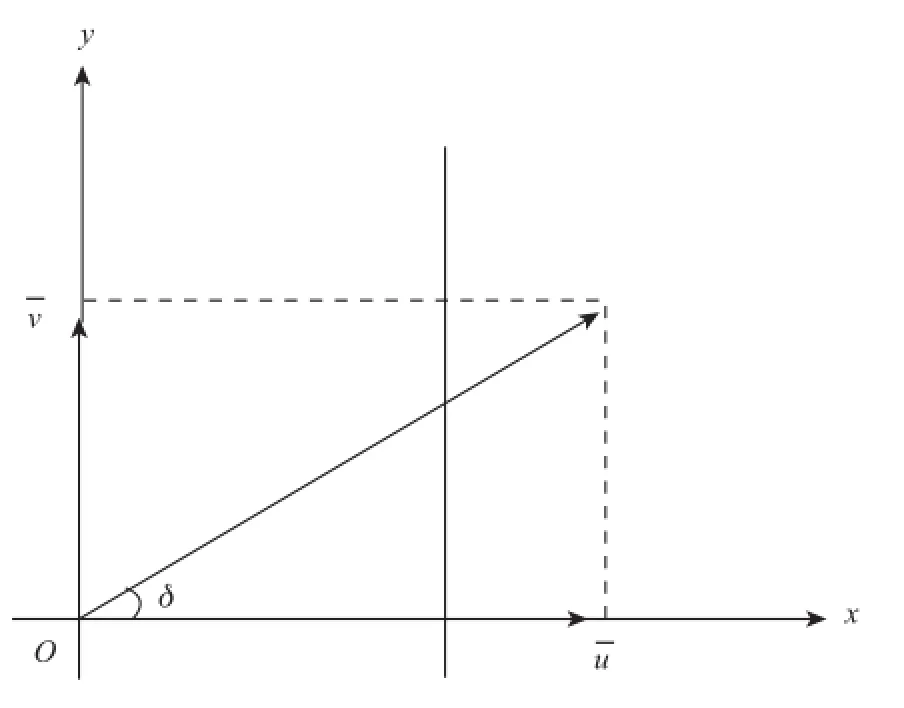
圖1剪切背景流U與內波傳播方向的示意圖

本文分析剪切背景流所導致的海洋波動不穩定發展的狀況，這里僅考慮小振幅波動的情形，因此可將上述Boussinesq方程組線性化。在文獻［18］中已給出該方程組以及線性化的過程，這里不再贅述。設波解為，這里T為矩陣轉置符號，代入該方程組后則可得到以下的常微分方程組［18-19］：

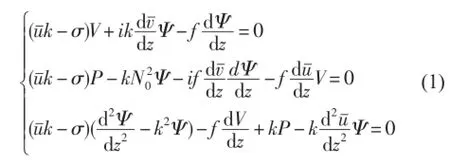
海面和海底均取水平剛璧，則有以下的上、下邊條件：

式中：常數H為海洋深度。這樣方程組（1）與邊界條件（2）構成一個變系數復常微分方程組的特征值問題，在此σ為特征值［18-19］。除極少數的特殊情況外（如無背景流且層結參數取常數的情況），該問題一般不能解析求解，為此可將其在垂直方向離散化，歸結為一個矩陣的特征值問題來近似求解，具體的操作過程可參見文獻［18］和［19］，這里也不再贅述。

數值求解該特征值問題可得到特征值（復頻率）σ，σ為一個復數，其實部為波動振蕩頻率，其虛部為不穩定波動的增長率（這里指該虛部大于0的情況，小于0的則為衰減率）；由此可知當σ不為實數時，波動可有不穩定發生。求解該問題得到的特征函數則分別給出了Ψ、V和Ρ在z方向的結構，而該特征函數乘以一個常數后仍為特征函數。在考慮所設波解后，就能得到海洋波動的結構［18-19］。

本文并不要求背景流的傳播方向與內波波陣面的法向（內波傳播方向）相一致，如上所述兩者可有一夾角δ，當δ=0°時，兩者方向相同，文獻［19］給出過此時長波長內波的計算結果，這也是研究得最多的情況。為敘述方便，仿照大氣動力學中的定義，可稱以上兩者方向相同的不穩定內波為橫波不穩定內波。另一種情況是內波的波陣面平行于背景流的流向（該波陣面的法向垂直于背景流），此時該夾角δ=90°，可稱此不穩定內波為對稱不穩定內波。而更普遍的情況是該夾角δ既不等于0°也不等于90°（見圖1），此時兩者方向斜交，可稱此時的不穩定內波為斜交不穩定內波。

由于本文只考慮不穩定海洋內波的流場結構，故僅給出流函數分布，此時圍繞流函數的正、負值中心分別有逆、順時針的流動［12-13］。在本文以下給出的流函數圖中，垂直方向取40層將海洋深度離散化，因為此時已能滿足精度要求［18-19］，而垂直坐標則用垂向分層序號n來表示，海底n=1，海面n=41，而其換算為與海底距離z的公式為z=H?（n-1）/40，在此H為海洋深度；在水平方向（內波波陣面的法方向，即x方向）則給出了兩個波長的計算結果，在此一個波長用33個格點表示，兩個則用65個格點表示；故在這些流函數圖中，橫坐標用水平格點序號l表示，l=1表示第1個水平格點，l=65表示第65個水平格點；l與水平距離 x的轉換公式為x=L?（l-1）/32，這里L為內波波長。

在計算中均取以下默認參數：內波波長L=1 000?m，這屬短波長的海洋內波。環境參數則取 f=10-4s-1和海水深度H=1 000?m。若不特別聲明，取默認層結參數，背景流則僅考慮線性垂直切變的情況，在默認情況下，取其在海面的流速為0.2 m/s，海底為0 m/s，此時該背景流的算術平均值為0.1 m/s。

3　　失穩內波流場結構和傳播情況分析

本節給出了不同斜交角情況下不穩定內波的增長率和傳播情況，并給出了x-z平面上相應的流函數分布。

3.1橫波不穩定海洋內波

圖2 a給出了取默認參數時，增長率為0.312 4× 10-5/s的最不穩定海洋內波在x-z平面上的流函數分布。該圖中縱坐標為垂向分層序號n，格點間距為25 m，橫坐標為水平格點序號l，格點間距為31.25 m。以下各圖坐標均與此相同，不再贅述。由該圖可見，此時該內波的流場主要分布在海洋上半層，并在垂直方向呈現兩個環流圈，即有貓眼結構。圖2b給出了增長率為0.308 7×10-5/s的次不穩定海洋內波的流函數分布，該次不穩定增長率與最不穩定的值很接近。由此圖可見，該內波的流場主要分布在海洋下半層，并也在垂直方向呈現兩個環流圈，即也有貓眼結構。比較圖2 a、2 b可見，兩者流場大致互為鏡像。相應兩者橫波不穩定的振蕩頻率分別為0.119 6×10-2/s和0.609 1×10-4/s，而對應的相速則分別為0.190 3 m/s和0.969 5×10-2m/s。在橫波不穩定的情況下，因斜交角為0°，平均背景流在波動等位相面法向（波動傳播方向）的投影就是其自身；將該最、次不穩定內波的相速減去該平均背景流的投影，即扣除該投影的多普勒效應，可得到相對于該投影的相速，可稱之為固有相速，其值分別為9.031 0× 10-2m/s和-9.030 5×10-2m/s，兩者的絕對值十分接近。由此可知，最、次不穩定內波分別是順、逆著該平均背景流（投影）傳播的，由內波波長和固有相速可得到該最、次不穩定內波的振蕩周期，不妨稱之為固有周期，其分別為3.075 8 h和3.075 9 h，表明此時最、次橫波不穩定內波均是高頻海洋內波。

當背景流和層結參數均取常數時，可得到該橫波型特征值問題的解析解［18］，當層結參數為正值時，內波是穩定的，并有：

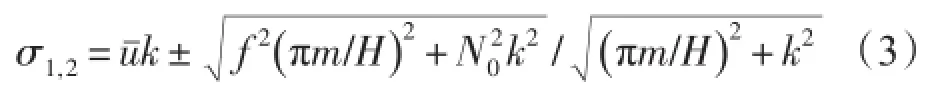
式中：m=1,?2,?…

通過以上分析，可以看出在文獻［19］中給出的橫波不穩定流場結構顯然與本文的流場結構不同。這主要是因兩者波長取得不相同所致（兩者環境參數取得相同或相近）。文獻［19］中取不穩定內波的波長為8 km和10 km，其波長比本文所取的大1個量級左右。比較本文與文獻［19］中的結果可見，橫波不穩定內波波長對其流場結構的影響很大，本文補充了橫波不穩定短波長內波的流場結構和傳播情況，也是對文獻［19］結果的重要補充。

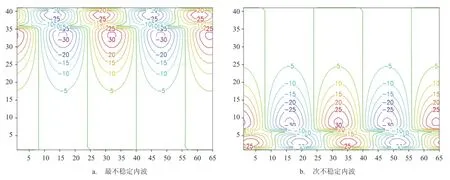
圖2 橫波不穩定內波的流函數（單位：m2/s）

3.2對稱不穩定海洋內波

仍取以上剪切背景流和層結參數的默認值，結果發現，這時得到的內波均是穩定（中性）的，無對稱不穩定出現。為考察對稱不穩定內波的流場和傳播，本文重新取了以下兩組參數做了計算。第1組層結參數仍取默認值，但增加了背景流的垂直切變，現取剪切背景流在海面的流速為0.4 m/s，海底仍為0 m/s。第2組剪切背景流仍取默認值，但減弱了層結參數，取層結參數N2為10-8/s2。取以上這兩組參數，則均有對稱不穩定發生。

取第1組參數，圖3給出了最不穩定海洋內波的流函數分布。此時最不穩定增長率為0.684 7× 10-4/s。由該圖可見，其流場表現為斜對流的形式，這種情況下流體微團在垂直方向是浮力（靜力）穩定的，在水平方向是慣性穩定的；然而其在傾斜方向則有不穩定發生，不穩定流場表現為傾斜的斜對流環流圈。在此，因對稱不穩定內波的等位相面平行于背景流方向，所以平均背景流在其等位相面法向的投影為0；這時其振蕩頻率為0，內波的傳播相速也為0，該對稱不穩定內波僅在原地增長而不傳播。

圖4 a給出取第2組參數時的計算結果，此時背景流的垂直切變值和層結參數值分別較圖3中減小了一半和一個量級。由圖4 a可見，該不穩定內波流場特征與圖3相似，也表現為傾斜環流圈。該最不穩定內波的增長率為0.884 9×10-4/s，其比圖3中的略大。與圖3中的一樣，此時對稱不穩定內波的振蕩頻率和波動相速均都為0，該內波也僅在原地增長而不傳播。圖4 b給出了取圖4 a中的參數后得到的對稱次不穩定內波的流場結構。與圖4 a不同的是，此時在垂直方向表現為兩個傾斜環流圈。該次不穩定內波的增長率為0.634 1×10-4/s，而其振蕩頻率和波動相速仍均都為0，不穩定內波同樣在原地增長而不傳播。從圖3、4的結果可見，對稱不穩定內波是不傳播而在原地增長，但此時穩定的內波還在傳播。比較圖4 a、4 b還可見，在相同參數下，垂直方向結構最簡單的對稱不穩定內波增長率最大。

圖3 對稱不穩定內波的流函數（單位：m2/s）

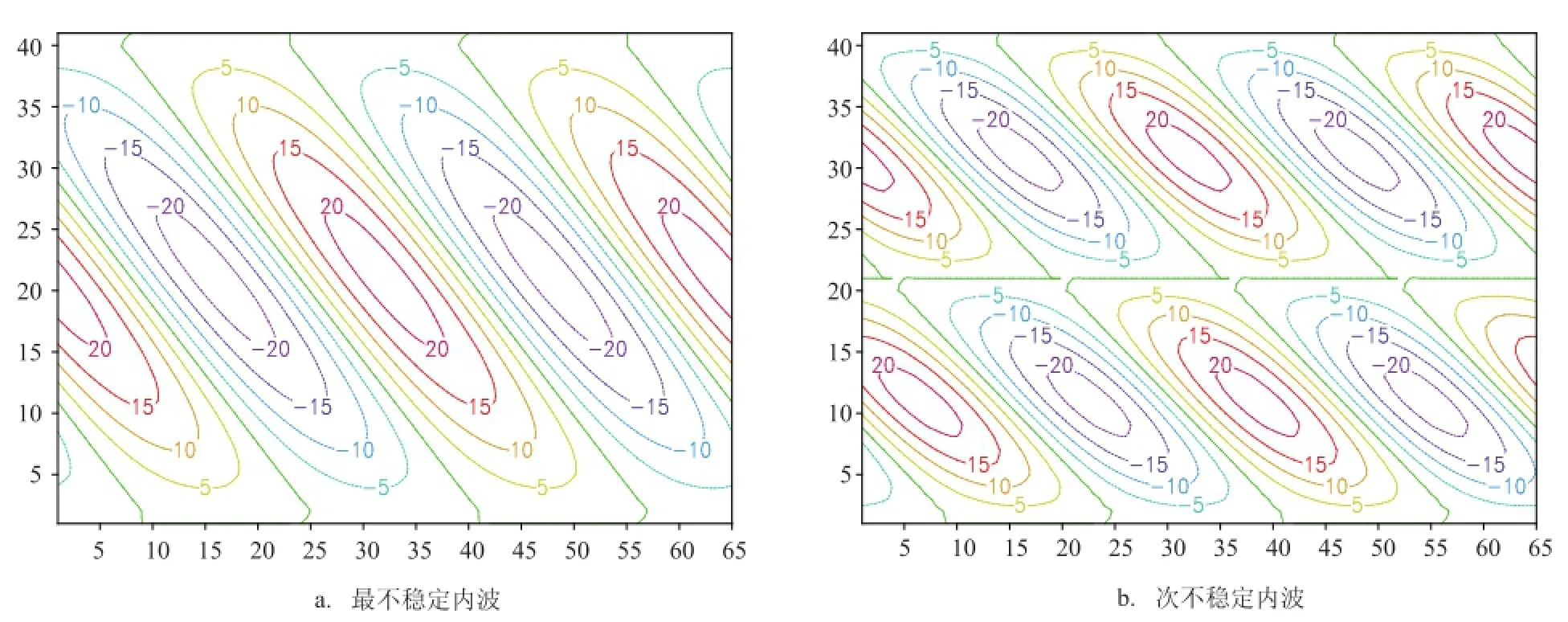
圖4改變背景流和層結參數后對稱不穩定內波的流函數（單位：m2/s）

3.3斜交不穩定海洋內波

取斜交角δ=60°，圖5a給出了取默認參數時，增長率為0.130 9×10-5/s的最不穩定內波流函數分布。由圖5a可見，該不穩定內波的流場主要分布在海洋中層，并在該處有一個明顯的環流圈，在該環流圈上方，還有流函數等值線密集的非常扁平的環流圈。圖5b給出了增長率為0.122 6×10-5/s的次不穩定內波流函數分布。由圖5b可見，該次不穩定內波的流場也主要分布在海洋中層，并在該處也有一個明顯的環流圈，在該環流圈下方，則有流函數等值線密集的非常扁平的環流圈。比較圖5 a、5 b，可見兩者的流場大致互為鏡像；兩者相應的斜交不穩定的振蕩頻率分別為0.591 3×10-3/s和0.371 2× 10-4/s，對應的相速則分別為0.941 1×10-1m/s和0.590 9×10-2m/s。考慮到該平均背景流在波動等位相面法向（波動傳播方向）的投影為0.1×cos60°= 0.05 m/s后，采用以上橫波不穩定內波的處理方法，可得到固有相速，其值分別為4.411 5×10-2m/s 和-4.409 1×10-2m/s，兩者的絕對值也十分接近；由此可知，該最、次斜交不穩定內波其分別是順、逆著該平均背景流投影傳播的。同樣可得到該最、次不穩定內波的固有周期值，其分別為6.296 7 h和6.300 0 h，兩者的值也十分接近，且也都為高頻海洋內波。

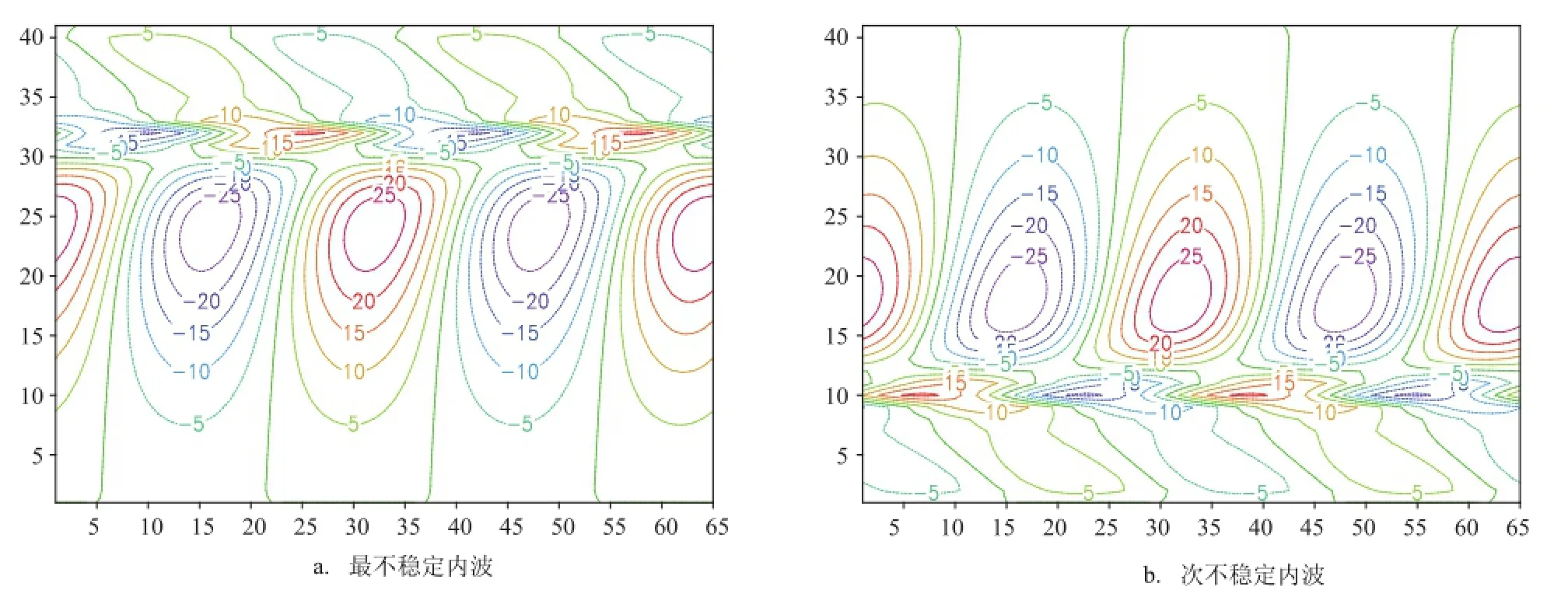
圖5 斜交角為60°時斜交不穩定內波的流函數（單位：m2/s）

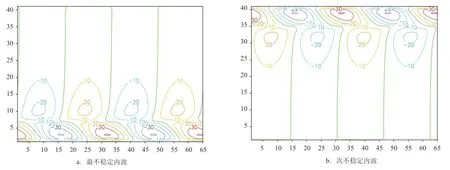
圖6斜交角為30°時斜交不穩定內波的流函數（單位：m2/s）

為考察斜交角改變后對斜交不穩定內波流場和傳播的影響，再取斜交角δ=30°和默認參數做了計算。圖6 a給出了增長率為0.305 1E×10-5/s的最不穩定海洋內波流函數分布。由圖6 a可見，該不穩定波動的流場主要分布在海洋下半層，并在垂直方向呈現兩個傾斜環流圈，也有貓眼結構，這與圖2 b的次不穩定橫波的結構有些類似。圖6 b給出了增長率為0.304 9×10-5/s的次不穩定內波流函數分布。由圖6b可見，該次不穩定波動的流場主要分布在海洋上半層，并在垂直方向也呈兩個傾斜環流圈，同樣也有貓眼結構，這與圖2 a的最不穩定橫波內波的結構有些類似。比較圖6 a、6 b可見，兩者流場同樣大致互為鏡像。這里斜交不穩定海洋內波與橫波不穩定海洋內波的結構有些類似，是因為斜交角δ不大。圖6a、b中斜交不穩定的振蕩頻率分別為0.553 2×10-4/s和0.103 3×10-2/s，而相應的相速分別為0.880 4×10-2m/s和0.164 4 m/s。在此平均背景流（0.1 m/s）在波動等位相面法向（波動傳播方向）的投影為0.1×cos30°=0.086 6 m/s。同樣采用以上橫波不穩定內波的處理方法，可得到固有相速，其值分別為-7.779 8×10-2m/s和7.780 3×10-2m/s，兩者的絕對值也十分接近；由此可知，該最、次斜交不穩定內波其分別是逆、順著該平均背景流投影傳播的，但這時最、次不穩定波動和背景流投影的配置則與圖5 a、5 b中的情況相反。同樣也可得到該最、次不穩定內波的固有周期值，其分別為3.570 5 h 和3.570 3 h，兩者的值也十分接近，且也都為高頻海洋內波。

4　　　結論

本文對剪切背景流導致的短波長海洋內波失穩做了分析，給出了該失穩內波的流場結構，討論了其傳播情況。所得主要結果為：

剪切背景流能造成短波長海洋內波的失穩，此時按照該失穩內波的波陣面的法向與背景流流向的夾角不同，可分為橫波不穩定，對稱不穩定和斜交不穩定3種情況，前兩種也是最后一種的特例。這3種情況下不穩定內波的流場呈現多種形態，對最不穩定流場而言，對稱不穩定內波流函數結構在傾斜方向呈現單圈環流的斜對流形態，而橫波不穩定內波和斜交不穩定內波的流函數結構則可有貓眼結構出現，此外在本文默認參數下，橫波不穩定內波增長率最大，斜交角為30°時斜交不穩定內波次之，斜交角為60°的斜交不穩定內波再次之，而無對稱不穩定內波出現（注意，本文中對稱不穩定內波取的環境參數不全為默認值）。對本文中的橫波不穩定內波和斜交不穩定內波而言，最不穩定的內波與次不穩定的內波兩者的流場分布幾乎互為鏡像。相應于本文所取的短波長內波，橫波不穩定和斜交不穩定的內波均為高頻內波，而對稱不穩定內波不傳播，其僅在原地增長，相同參數下垂直方向結構最簡單的對稱不穩定內波其增長率最大。

本文僅局限于討論層結參數為常數的失穩內波流場和傳播的理論分析，雖然實際海洋中也有此種情況，但畢竟海洋中躍層的存在是較普遍的情況；故而討論海洋存在躍層時剪切背景流下的內波失穩問題更有實際意義。我們已開始在該方面做了部分工作，該工作全部完成后將另文介紹。

參考文獻：

［1］Staquet C，Sommeria J.INTERNAL GRAVITY WAVES：From Instabilities to Turbulence［J］.Annual Review of Fluid Mechanics，2002，34（1）：559-593.

［2］Yang Y J，Fang Y C，Chang M H，et al.Observations of Second Baroclinic Mode Internal Solitary Waves on the Continental Slope of the Northern South China Sea［J］.Journal of Geophysical Research，2009，114（C10）：C10003，doi：10.1029/2009JC005318.

［3］Kunze E，MacKay C，McPhee-Shaw E E，et al.Turbulent Mixing and Exchange with Interior Waters on Sloping Boundaries［J］. Journal of Physical Oceanography，2012，42（6）：910-927.

［4］Venayagamoorthy S K，Fringer O B.Nonhydrostatic and Nonlinear Contributions to the Energy Flux Budget in Nonlinear Internal Waves［J］.Geophysical Research Letters，2005，32（15）：L15603.

［5］Vlasenko V，Stashchuk N，Guo C S，et al.Multimodal Structure of Baroclinic Tides in the South China Sea［J］.Nonlinear Processes in Geophysics，2010，17（5）：529-543.

［6］Lelong M P，Kunze E.Can Barotropic Tide/Eddy Interactions Excite Internal Waves？［J］.Journal of Fluid Mechanics，2013，721：1-27.

［7］Kunze E.The Relation between Unstable Shear Layer Thicknesses and Turbulence Lengthscales［J］.Journal of Marine Research，2014，72（2）：95-104.

［8］Alford M H，Peacock T，MacKinnon J A，et al.The Formation and Fate of Internal Waves in the South China Sea［J］.Nature，2015，521 （7580）：65-69.

［9］范植松，高郭平，尹訓強，等.具有內波特性的渤海南部次重力波［J］.海洋學報，2003，25（5）：136-140.

［10］Yuan Y L，Zheng Q A，Dai D J，et al.Mechanism of Internal Waves in the Luzon Strait［J］.Journal of Geophysical Research：Oceans，2006，111（C11）：C11S17，doi：10.1029/2005JC003198.

［11］Rainville L，Pinkel R.Observations of Energetic High-Wavenumber Internal Waves in the Kuroshio［J］.Journal of Physical Oceanography，2005，34（7）：1495-1505.

［12］Charney J G.The Dynamics of Long Waves in A Baroclinic Westerly Current［J］.Journal of Meteorology，1947，4（5）：135-162.

［13］Kuo H L.Three-Dimensional Disturbances in A Baroclinic Zonal Current［J］.Journal of Meteorology，1952，9：260-278.

［14］曾慶存，李榮鳳，張銘.旋轉二維可壓縮流動的譜和特征函數Ⅰ：譜點的分布［J］.大氣科學，1990，14（2）：129-142.

［15］曾慶存，李榮鳳，張銘.旋轉二維可壓縮流動的譜和特征函數Ⅱ：譜和譜函數結構的分析［J］.大氣科學，1991，15（1）：1-15.

［16］張立鳳，張銘.斜壓切變基流中橫波型擾動的特征波動Ⅱ：譜函數［J］.氣象學報，2001，59（2）：143-156.

［17］張銘，張立鳳，安潔.大氣波譜分析及其不穩定性（第一卷）：二維旋轉層結大氣中的擾動［M］.北京：氣象出版社，2008.

［18］鄧冰，張銘.海洋內部波動的波譜和譜函數.I-數學模型和計算方法［J］.水動力學研究與進展，2006，21（2）：259-266.

［19］鄧冰，張翔，張銘.海洋內重力慣性波不穩定模態分析［J］.海洋預報，2014，31（1）：36-41.

中圖分類號：P731.21

文獻標識碼：A

文章編號：1003-0239（2016）03-0001-08

DOI：10.11737/j.issn.1003-0239.2016.03.001

收稿日期：2015-08-28

基金項目：國家重點研究發展計劃（“973”計劃，2013CB956203）。

作者簡介：鄧冰（1963-），女，高級工程師，博士，主要從事物理海洋學研究。E-mail:dbing039@163.com直切變基本流的斜壓非地轉、非靜力大氣，討論了該大氣的穩定性問題以及其波譜問題［16-17］。大氣和海洋均屬地球流體，雖然其控制方程組和物理參數略有不同，但用該數值求解方法討論海洋內波的穩定性問題并無原則上的困難［18］。在有關海洋內波失穩的研究中，大多討論海洋內波的傳播方向與剪切背景流方向一致的情況，然而這兩者的方向也可以不同，如上文Yuan等［10］分析的情況；對于波動傳播方向與背景流流向不同的情況，雖在大氣中已有較多的討論［16-17］，但對海洋內波目前尚不多見。

Theoretical analysis on the stream structure and propagation of unstable ocean internal wave at background shear flow

DENG Bing1，ZHANG Yu-fei2，ZHU Juan3，ZHANG Ming4
（1.Beijing Applied Meteorology Institute，Beijing 100029 China；2.College of Marine Environment，Ocean University of China，Qingdao 266003 China；3.Unit 61139，P.L.A，Beijing 100081 China；4.PLA University of Science and Technology meteorological and Oceanographic Institute，Nanjing 211101 China）

Abstract：The unstable short wavelength ocean internal wave caused by the background shear flow is studied，as well as its stream structure and propagation by using the method of solving eigenvalue.According to the different angle between normal phase front and background flow of unstable wave，there are three types of instability，which are transversal instability（angle of 0 degree），symmetrical instability（90 degree）and heterotropic instability（arbitrary angle）.Accordingly，the stream field of each unstable ocean internal wave appears differently.To the most unstable stream field，the shape of symmetrically unstable internal wave is a kind of sideling convection with single circle.While the shape of transversally unstable internal wave and heterotropically unstable internal wave appear a cat's eye structure.With regard to the transversally unstable internal wave and heterotropically unstable internal wave，the stream fields distribution are nearly mirror images in the most unstable stream field and the second unstable stream field.To the short wavelength internal wave studied in this paper，the transversally and heterotropically unstable internal waves are all in the high frequency. While the symmetrically unstable internal wave cannot propagate but grows only in situ.The symmetrically unstable internal wave with simplest structure has the biggest growing rate on the condition of the same parameters.

Key words：background shear flow；unstable ocean internal wave；stream structure；propagation