基于一種新流水步距的工期優(yōu)化分析*
吳 韜汪 梅王艷華李海霞
(1.安徽新華學(xué)院土木與環(huán)境工程學(xué)院 安徽合肥 230088;2.合肥前城置業(yè)有限公司造價(jià)部 安徽合肥 230088)
?
基于一種新流水步距的工期優(yōu)化分析*
吳 韜1汪 梅2王艷華1李海霞1
(1.安徽新華學(xué)院土木與環(huán)境工程學(xué)院 安徽合肥 230088;2.合肥前城置業(yè)有限公司造價(jià)部 安徽合肥 230088)
摘 要:傳統(tǒng)流水施工組織方法在工程應(yīng)用中存在工期較長(zhǎng)、分層組織時(shí)主導(dǎo)施工過(guò)程不能連續(xù)作業(yè)等缺陷。為有效解決上述問(wèn)題,本文重新界定了流水步距的含義,并引入了逆流水步距概念,從而重新構(gòu)建了流水工期表達(dá)式。該表達(dá)式與流水工期的定義形式具有相同的構(gòu)造組成,可較為方便地更新現(xiàn)有《施工組織》教材中流水施工的相應(yīng)理論知識(shí)點(diǎn),且實(shí)例應(yīng)用表明,基于新型流水步距的工期優(yōu)化可以實(shí)現(xiàn)工期與資源綜合最優(yōu)的效果,且工期縮短與費(fèi)用增加可以實(shí)現(xiàn)量化評(píng)價(jià)。
關(guān)鍵詞:流水施工 流水步距 工期優(yōu)化 異步距異節(jié)拍
一、問(wèn)題的提出
流水施工是現(xiàn)代施工管理領(lǐng)域中最科學(xué)的施工組織方法之一,并已在各類型的工程建設(shè)中得到了廣泛應(yīng)用,工程實(shí)踐表明,科學(xué)合理地應(yīng)用流水施工原理可以實(shí)現(xiàn)資源供應(yīng)均衡、工期有效縮短、施工質(zhì)量專業(yè)化等綜合效益。土木類施工或施工組織的經(jīng)典教材[1-3]介紹了流水施工的基本原理,如流水施工基本概念、流水參數(shù)、流水組織方式等,其中流水步距作為基本流水參數(shù),同時(shí)也是間接性參數(shù),在流水組織過(guò)程及實(shí)現(xiàn)流水工期效益中發(fā)揮著重要作用。也一直是流水施工原理的研究熱點(diǎn)[4-6]。傳統(tǒng)的流水步距有兩種定義:其一是指相同施工過(guò)程的施工班組先后進(jìn)入同一個(gè)施工段開(kāi)始施工的最小且合理的時(shí)間間隔(不包括間歇和搭接)[3],其二是指相鄰施工班組先后入場(chǎng)的最小且合理的時(shí)間間隔(不包括間歇和搭接)[1]。第一種定義在應(yīng)用于成倍節(jié)拍流水時(shí),與其流水特性不協(xié)調(diào),因?yàn)槌杀豆?jié)拍流水的流水步距均相等的這一特性已成為行業(yè)共識(shí),而依據(jù)第一種定義顯然與此特性矛盾,因此第二種定義逐漸被學(xué)界和工程界所認(rèn)同。依據(jù)第二種定義,“最小且合理”的含義主要體現(xiàn)出如下特點(diǎn):(1)施工班組最大限度實(shí)現(xiàn)連續(xù)作業(yè);(2)相鄰施工過(guò)程盡可能平行搭接施工;(3)工作面盡可能連續(xù)利用。當(dāng)組織等步距流水(全等節(jié)拍流水和成倍節(jié)拍流水)時(shí),不分層時(shí)以上特點(diǎn)可理想化表現(xiàn),而分層時(shí)則一般需要滿足施工段數(shù)的限制;當(dāng)組織異步距流水(異步距異節(jié)拍流水和無(wú)節(jié)奏流水)時(shí),以上特點(diǎn)很難完全體現(xiàn),不分層時(shí)考慮班組連續(xù)作業(yè)則工期會(huì)相對(duì)較長(zhǎng),且工作面閑置較長(zhǎng),如圖1所示,分層時(shí)甚至連“主導(dǎo)施工過(guò)程連續(xù)作業(yè)”的關(guān)鍵流水條件也不能滿足[7],如圖2所示。工程實(shí)踐中一般會(huì)在圖1的基礎(chǔ)上進(jìn)行局部調(diào)整,如圖3所示,但這種調(diào)整缺乏理論依據(jù),調(diào)整后的流水工期不能直接應(yīng)用其定義公式(1)校核評(píng)價(jià)。式中,,1i iK+為流水步距,NT 為最后一個(gè)班組的作業(yè)持續(xù)時(shí)間,1Z為首層層內(nèi)所有間歇與搭接的代數(shù)和。
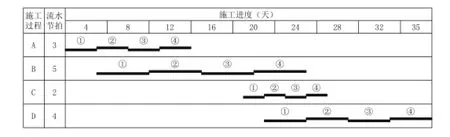
圖1 不分層時(shí)的流水施工橫道圖(工期較長(zhǎng))

圖2 分層時(shí)的流水施工橫道圖(主導(dǎo)施工過(guò)程層間作業(yè)不連續(xù))
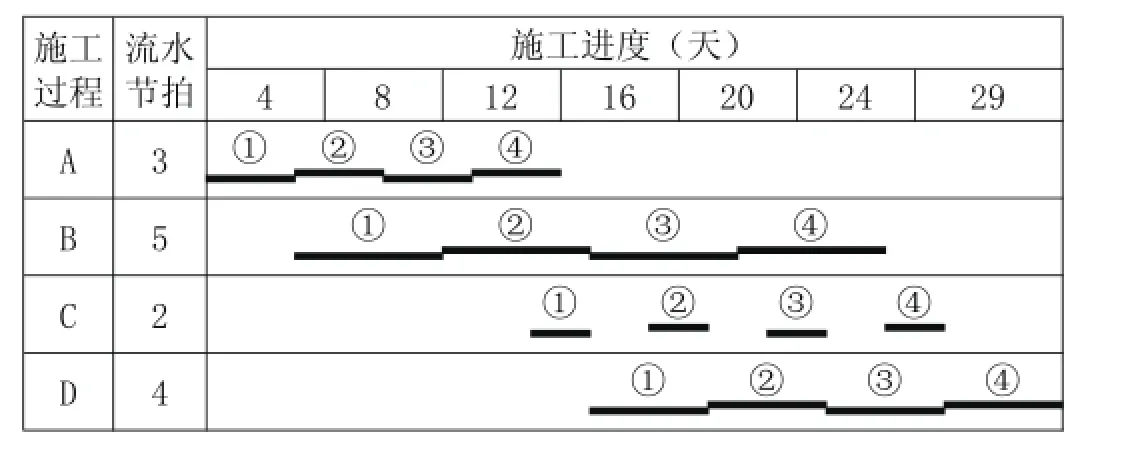
圖3 不分層時(shí)的流水施工調(diào)整橫道圖(工期較短)
二、逆流水步距與流水工期優(yōu)化原理
1.逆流水步距
為解決上述問(wèn)題,尤其是異步距異節(jié)拍流水的施工組織及工期計(jì)算問(wèn)題,本文建議適當(dāng)調(diào)整流水步距定義中“最小且合理”的含義,即將基于班組連續(xù)作業(yè)的前提改變?yōu)榛诠ぷ髅孢B續(xù)利用,并引入“逆流水步距”參數(shù)[7],所謂逆流水步距是指相鄰施工班組先后退場(chǎng)的最小且合理的時(shí)間間隔(不包括間歇和搭接),用表示,當(dāng)有N個(gè)施工班組時(shí),逆流水步距的數(shù)目為(N-1)。
于是,流水步距和逆流水步距可分別按照式(2)和式(3)計(jì)算,如圖4所示,能滿足關(guān)鍵條件“主導(dǎo)施工過(guò)程連續(xù)作業(yè)”的約束。
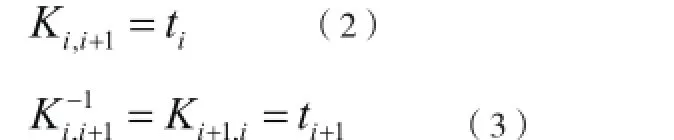
式中,it為第i個(gè)施工過(guò)程的流水節(jié)拍,1it+為第i+1個(gè)施工過(guò)程的流水節(jié)拍。
2.流水工期優(yōu)化原理
重新界定流水步距含義及引入逆流水步距后的橫道圖如圖4所示,比較圖3和圖4可知,兩者工期相同,而圖3可理解為在基于工作面連續(xù)利用的前提下實(shí)現(xiàn)最大程度的班組連續(xù)作業(yè)和施工過(guò)程最大限度的平行搭接。因此流水工期可參照?qǐng)D4,并依據(jù)定義公式(1)的概念化結(jié)構(gòu)建立其表達(dá)式(4),進(jìn)一步地,代入式(2)、(3)后,式(4)可簡(jiǎn)化成式(5)。

式中,m為施工段數(shù),maxt為主導(dǎo)施工過(guò)程的流水節(jié)拍,其他符號(hào)與前文同。
于是,在資源總量不變的情況下,合理最短的工期可根據(jù)式(5)直接確定,而最優(yōu)進(jìn)度橫道圖可參照“圖4→圖3”的優(yōu)化思路分兩步繪制。
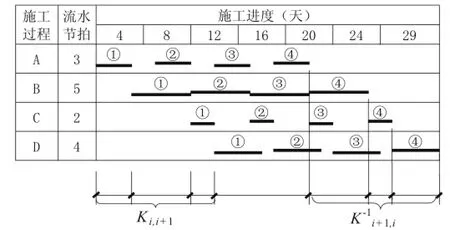
圖4 流水步距與逆流水步距
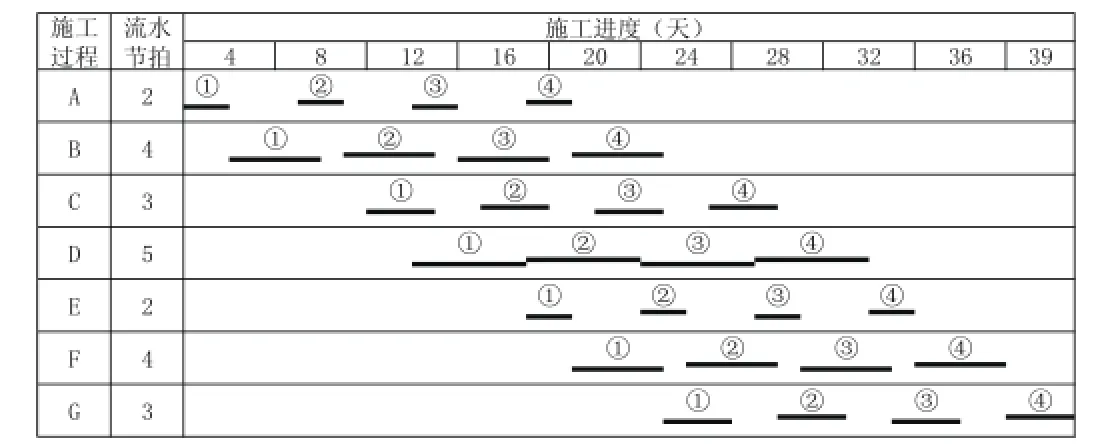
圖5 基于工期最優(yōu)原則繪制的橫道圖

圖6 基于工期和資源綜合最優(yōu)原則繪制的橫道圖
三、應(yīng)用分析
某工程按照異步距異節(jié)拍流水組織施工,包括施工過(guò)程A、B、C、D、E、F、G,含4個(gè)施工段,不分層,各施工過(guò)程的流水節(jié)拍分別為2、4、3、5、2、4、3,B、C之間存在2天技術(shù)間歇,C、D之間存在1天組織搭接。
依據(jù)式(5)計(jì)算流水工期為39天,而依據(jù)式(1)計(jì)算的流水工期為48天,可見(jiàn)應(yīng)用本文的優(yōu)化方法工期縮短了9天,降幅達(dá)18.75%。
基于工作面連續(xù)的新流水步距及其他流水參數(shù),繪制橫道圖(即工期最優(yōu)原則)如圖5所示,再按照?qǐng)D3的傳統(tǒng)思路盡量壓縮班組作業(yè)的不連續(xù)時(shí)間,優(yōu)化后的橫道圖(即工期和資源綜合最優(yōu)原則)如圖6所示。
圖6反映了C、D之間組織搭接參數(shù)的目的是為了組織D班組提前入場(chǎng)施作第一個(gè)施工段,以縮短工期,此后施工段可不考慮搭接關(guān)系;且圖6中班組作業(yè)不連續(xù)的總時(shí)間為9天,正好等于按式(5)和式(1)計(jì)算的工期縮短差值,由此也可以獲得進(jìn)一步的結(jié)論,即在不考慮間歇和搭接的前提下,依據(jù)(5)計(jì)算得到的最優(yōu)工期減少值即為班組作業(yè)不連續(xù)時(shí)間,這一結(jié)論不僅是初始橫道圖優(yōu)化的目標(biāo),還可作為工期縮短與成本增加綜合效益分析的評(píng)價(jià)指標(biāo)。
四、結(jié)論
本文在不改變流水參數(shù)具體數(shù)值的前提下,基于最優(yōu)流水工期為目標(biāo),重新界定了流水步距的含義,并引入了逆流水步距,進(jìn)而建立了流水工期新的簡(jiǎn)明計(jì)算表達(dá)式,結(jié)合不分層時(shí)的異步距異節(jié)拍流水施工組織實(shí)例表明,本文提出的新型流水步距可以實(shí)現(xiàn)最短工期及其量化的優(yōu)化目標(biāo),不僅完善了現(xiàn)有傳統(tǒng)教材中關(guān)于流水施工的理論知識(shí),而且在實(shí)例中采用的施工組織方法與思路可以直接應(yīng)用于工程實(shí)踐。
參考文獻(xiàn):
[1]重慶大學(xué),同濟(jì)大學(xué),哈爾濱工業(yè)大學(xué).土木工程施工[M],北京:中國(guó)建筑工業(yè)出版社,2008.
[2]于立君,孫寶慶.建筑工程施工組織[M],北京:高等教育出版社,2014.
[3]危道軍.建筑施工組織[M],北京:中國(guó)建筑工業(yè)出版社,2013.
[4]魯雷,崔秀琴.流水步距定義問(wèn)題的分析[J],焦作大學(xué)學(xué)報(bào),2007,(1):92-93.
[5]何夕平.搭接與間歇對(duì)流水施工工期影響分析[J],四川建筑科學(xué)研究,2004,30(2):107-108.
[6]續(xù)憲宏,向健.關(guān)于流水步距和流水工期計(jì)算方法的討論[J],甘肅科技,2007,23(6):155-156,66.
[7]吳韜,張文振,張劼,等.基于逆流水步距組織分層無(wú)節(jié)奏流水施工[J].合肥學(xué)院學(xué)報(bào)(自然科學(xué)版),2014,24(1):92-96.
本文創(chuàng)新點(diǎn):
1.重新界定了流水步距的含義
2.引入逆流水步距參數(shù),并提出其計(jì)算方法
3.基于新的流水步距和逆流水步距,構(gòu)建了最優(yōu)流水工期的計(jì)算表達(dá)式
4.提出基于工期和資源綜合優(yōu)化的流水施工組織方法
作者簡(jiǎn)介:
吳韜(1982-),男,安徽東至人,安徽新華學(xué)院土木與環(huán)境工程學(xué)院講師,碩士,研究方向:工程結(jié)構(gòu)動(dòng)力分析與防震減災(zāi)。
*基金項(xiàng)目:安徽省教育廳教研項(xiàng)目(2012jyxm584);安徽新華學(xué)院教研項(xiàng)目(2013jy036);安徽新華學(xué)院骨干教師資助項(xiàng)目(2012xgg03)。

