基于響應面更新的飛行器協同優化方法

池元成 王彥靜 董 偉 陸小兵 郭會章

中國運載火箭技術研究院研究發展中心, 北京 100076

?

基于響應面更新的飛行器協同優化方法

池元成 王彥靜 董 偉 陸小兵 郭會章

中國運載火箭技術研究院研究發展中心, 北京 100076

飛行器總體設計是一項復雜系統工程，多專業、強耦合是其特點。針對飛行器總體快速設計需求，提出基于響應面更新的協同優化方法。通過將臨時最優解納入輸入輸出樣本對方法，逐步更新響應面模型，并利用協同優化方法對復雜系統進行分解尋優。以某飛行器為應用對象進行優化設計，結果表明該方法能夠快速獲得最優解，提高求解效率。 關鍵詞 飛行器總體設計；協同優化；響應面；試驗設計

飛行器總體設計是一項復雜系統工程，涉及多專業、多變量和多約束，直接影響飛行器的作戰性能、研制周期和經費等，在飛行器整個研制過程中具有重要地位。飛行器總體設計是根據戰技要求和各項技術發展現狀，對飛行器及其各系統進行綜合、協調、研究和設計的過程，往往經過多次迭代，才能得到綜合性能最佳的飛行器總體方案[1]。

多學科優化設計(Multidisciplinary Design Optimization，MDO)最早是由Sobiesky提出[2]。由于MDO充分考慮了復雜系統內部的耦合關系，利用分級方式將強耦合降低為低耦合，各子系統優化的同時完成系統級優化，最終完成復雜系統優化。因此，非常適合求解各類復雜系統優化問題[3～5]。目前，MDO發展出了協同優化方法(Collaborative Optimization，CO)、并行子空間優化方法(ConCurrent Subspace Optimization，CSSO)、雙層集成系統綜合(Bi-Level Integrated System Synthesis，BLISS)和解析目標分流(Analytical Target Cascading，ATC)等方法，分別在各個領域發揮了作用。

本文提出的方法根據優化結果逐步更新近似模型，從而找到問題的最優解。為了研究和分析該方法的正確性，以某飛行器總體設計作為優化目標，以協同優化方法和響應面方法為研究對象，在基于近似模型的協同優化方法獲得問題的最優解之后，將最優解代入原仿真模型，并更新近似模型，再根據更新后的近似模型利用協同優化方法進行優化設計，重復上述過程直到找到問題的最優解。

1 協同優化方法

協同優化方法[6]作為代表性的MDO方法之一，主要根據專業對復雜系統優化問題進行分解、協調和優化，是一個典型的系統協調優化方法，其結構簡單且算法收斂性相對可靠。

CO是一個典型的上下2層結構：系統級和學科(專業)級，如圖1所示。CO的設計思想是在進行學科(專業)級優化時，各學科單獨優化而不考慮其他學科的影響，只須滿足各自學科的約束，獨立進行學科分析與決策。學科(專業)級的優化目標是使該學科(專業)的方案與系統級傳遞的設計目標差異最小。而每個學科級優化結果的不一致性統一由系統級協調，通過系統級和學科級之間多次優化迭代，最終找到符合學科間一致性要求的一個系統最優設計方案。

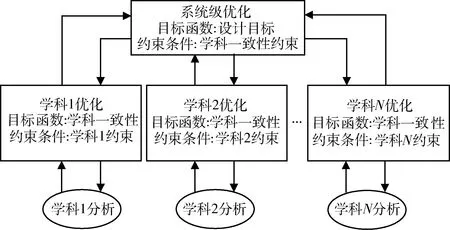
圖1 CO的結構

2 響應面方法

在對仿真模型進行計算分析與優化過程中往往要引入近似模型技術。近似模型技術利用有限的仿真模型的輸入輸出參數對，通過擬合方法建立的數學模型，是對原模型進行二次建模后的模型。近似模型可以減少計算耗時，快速分析模型復雜度和參數靈敏度。目前，常用的近似模型方法包括響應面方法(Response Surface Methodology，RSM)、神經網絡(Neural Network，NN)和支持向量機(Support Vector Machine，SVM)等。

RSM[7]是將試驗設計與數理統計相結合的方法，用于描述多個設計變量對目標變量的影響，最早由數學家Box和Wilson于1951年提出，是解決復雜工程問題的有效方法。工程中通常采用二階響應面模型，對k個隨機變量的情況，二階響應面模型的一般公式為

(1)

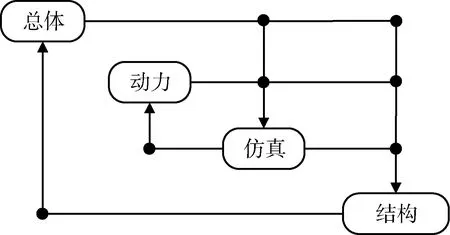
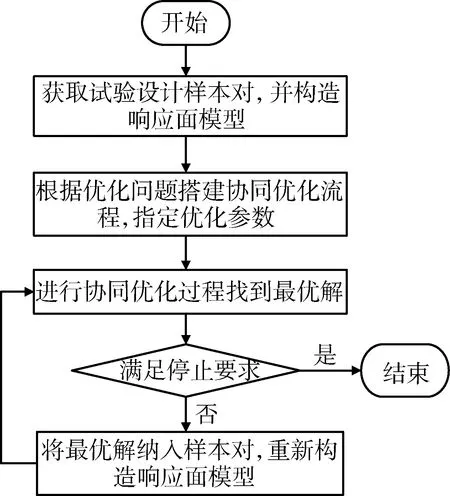
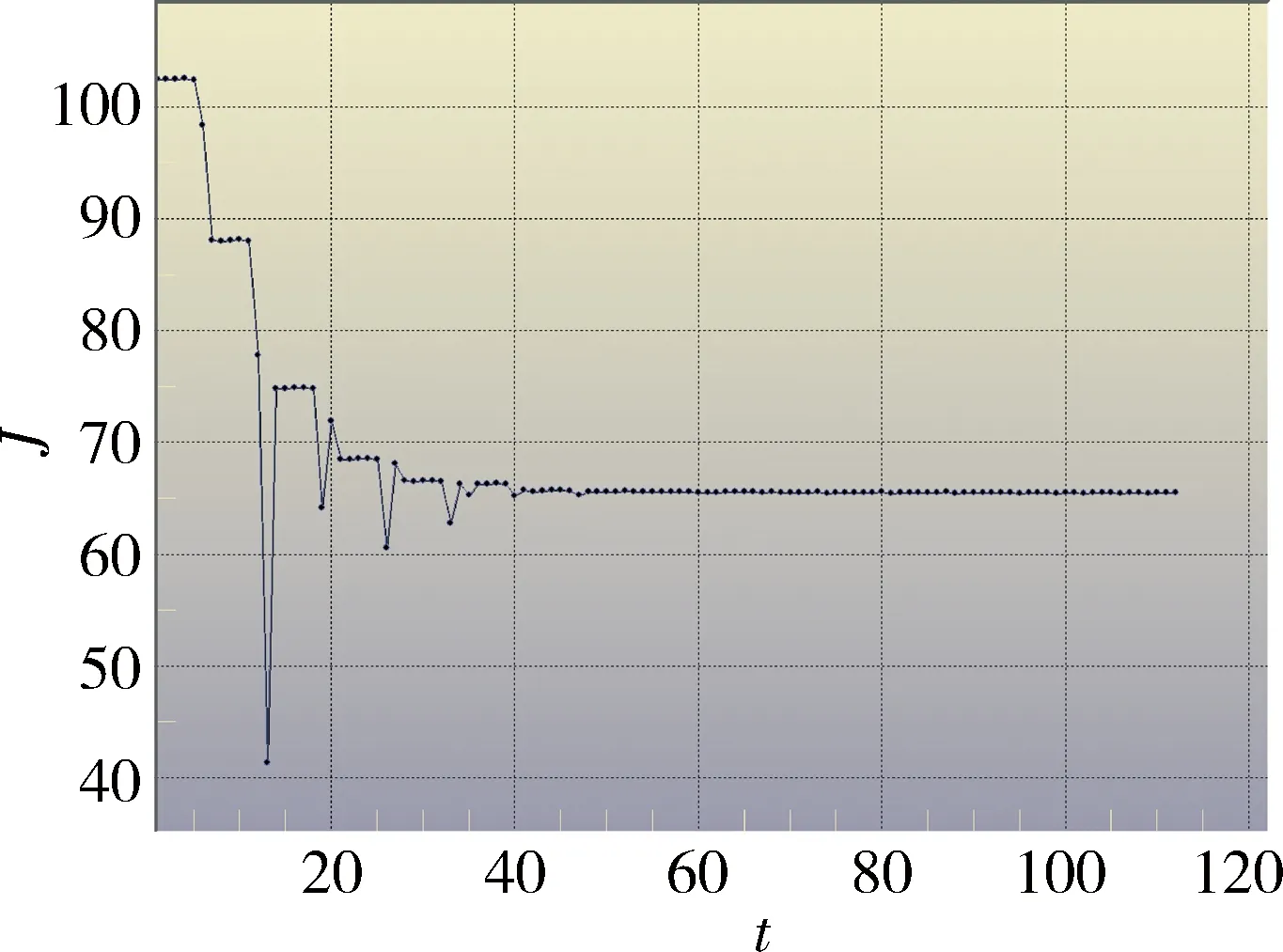
式中，y為模型輸出變量；x為模型輸入變量；βi，βii，βij為待定系數；i

3 基于響應面更新的協同優化方法

隨著對飛行器設計要求的提高，在其設計過程中引入了仿真技術，以驗證飛行器在模擬環境下的各項性能。為獲得更加準確的設計效果，越來越多的采用了高精度仿真模型。然而，這大大降低了優化效率。因此，文獻[8]提出了一種迭代更新的近似模型生成方法，首先利用試驗設計建立初步近似模型，再根據梯度、波動等特征產生補充訓練集，以便更新近似模型，最后將該方法應用于導彈總體優化設計中，用于近似精確啟動計算；文獻[9]比較了響應面模型、Kriging模型和RBF模型的性能，并基于每經過一定次數的迭代更新方法更新近似模型，雖然一定程度上提高了優化效率，但調用計算模型的次數依然較多；文獻[10]提出了基于近似模型的兩級集成系統協同優化方法，其中子系統近似模型的構建在子系統級優化之前，避免了每一次系統優化都要進行繁多的子系統分析等，利用近似模型代替原計算模型，最終獲得了最優解。然而，所獲得的最優解均是基于近似模型，在近似模型對原模型的近似程度相對較高的情況下，可以認為該最優解是原問題的最優解。但是，若近似模型對原模型近似程度不夠時，需要進一步對近似模型更新以提高其近似程度。為此，本文提出了基于響應面更新的協同優化方法。該方法首先利用試驗設計獲取設計變量分布，并通過高精度仿真模型計算輸出值，形成初設近似建模樣本對；然后，使用響應面方法對初設樣本對進行建模，產生近似模型；再利用協同優化方法基于近似模型對優化問題進行尋優，找到最優解x*，分析x*是否為最優解，這一過程可將最優解x*代入高精度仿真模型，比較輸出結果與最優值的差是否在可接收范圍內，若滿足要求則停止尋優，最優解即為x*；若不滿足要求，則將最優解x*納入初設近似建模樣本對，再利用響應面方法建模，之后依然利用協同優化方法進行求解。如此往復，直到找到全局優化解。

通過近似模型更新過程，只需在近似建模過程中調用多次高精度仿真模型。此后，只需對最優解x*進行驗證過程時調用高精度仿真模型，這樣能大大減少調用高精度仿真模型的次數，節省優化時間，而且也能保證近似模型的局部精確性。

在上述分析的基礎上，給出基于響應面更新的協同優化方法的具體步驟，如下所示：

步驟1：針對仿真模型的設計變量利用試驗設計方法計算相應輸出變量值，取得近似建模輸入輸出樣本對；

步驟2：利用輸入輸出樣本對采用響應面方法構造近似模型；

步驟3：構造協同優化流程，指定優化問題的各參數；

步驟4：運行協同優化過程，獲得最優解x*；

步驟5：將x*代入仿真模型，計算相應輸出值y*，若滿足要求則退出，否則轉步驟6；

步驟6：將(x*,y*)添加至近似建模輸入輸出樣本對，返回步驟2。

4 優化結果與分析

某飛行器總體設計過程涉及動力、結構及機動仿真等組成，首先通過結構設計矩陣梳理了各專業之間的參數傳遞關系與具體傳遞參數，并搭建了飛行器總體方案設計流程，其設計結構矩陣如圖2所示。

圖2 總體設計結構矩陣

為了達到設計要求，以起飛質量(M)最小以及飛行距離(L)最大為優化目標，本文中考慮的是單目標優化問題，為此構建了指標函數如下

J=J(M,L)=ε×M+(1-ε)×L

(2)

其中，ε為協調參數取[0,1]之間的值，通過ε的值協調起飛質量與飛行距離在優化目標中的影響程度。在本文的算例中，ε=0.5，即起飛質量和飛行距離的貢獻程度相同。如果考慮不同的影響程度時，可通過改變ε的值實現。

在此基礎上，構建基于響應面更新的協同優化流程如圖3所示。

圖3 優化流程圖

本文選取了一個初始可行點作為優化起步點，其信息如表1所示。

表1 初始點

經過基于響應面的協同優化之后，得到了滿足約束的最優解X*，將X*代入高精度仿真模型得到的信息如表2所示。

進一步，將表2中的最優解加入到輸入輸出樣本點，重新基于響應面方法構造近似模型，并基于更新后的近似模型重新進行協同優化，且優化起步點為初始可行點。經過基于響應面更新的協同優化之后，得到了滿足約束的最優解X**，將X**代入高精度仿真模型得到的信息如表3所示。

表2 最優解

表3 更新最優解

基于響應面更新的協同優化方法在飛行器總體優化設計過程如圖4所示，其中縱坐標為目標函數J，橫坐標為迭代次數t。

圖4 優化迭代圖

由表1～3可知，基于響應面更新的協同優化方法能夠找到最優的設計結果，相比于初始點，基于響應面更新的協同優化方法提高了32.4%，相比于基于響應面的協同優化方法提高了6.6%，而且隨著這一過程的重復進行能夠更加精確的找到問題的最優解。此外，從計算效率上看，一次完整的仿真過程需要耗費2個多小時，如果直接基于高精度仿真模型進行優化，至少要運行1個星期，而基于響應面更新的協同優化能夠在1h內完成。可知，該方法大大提高了優化效率和求解精度。

5 結論

為了滿足飛行器總體快速設計需求，提出了基于響應面更新的協同優化方法，將臨時解作為輸入輸出樣本對之一，通過逐步更新響應面模型的方式，提高了近似模型的精度，利用協同優化方法針對復雜系統解耦的特點，對原求解問題進行分解，提高了全局搜索效率。最后，以某飛行器總體設計為實例，驗證了該方法的有效性，求解結果能滿足應用需求。

[1] 侯世明.飛行器總體設計與試驗[M].北京: 宇航出版社, 1996.(Hou Shiming. Missile Total Design and Test [M].Beijing: China Astronautics Press, June, 1996.)

[2] AIAA White Paper . Current State of the Art: Multidisciplinary Design Optimization [R]. Washington: AIAA Technical Committee for MDO. 1991.

[3] Robert W. Roe, Sean T. Ford, Gokcin Cinar, et al. A Multi-Disciplinary Integrated Design Environment for Requirements Development and Performance Evaluation of Autonomous Systems [R]. 14th AIAA Aviation Technology, Integration, and Operations Conference, 2014.

[4] T. Zill, P. D. Ciampa, B. Nagel. A Collaborative MDO Approach for the Flexible Aircraft [R]. 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, 2013.

[5] C. Davies, M. Stelmack, S. Zink, et al. High Fidelity MDO Process Development and Application to Fighter Strike Conceptual Design [R]. 12th AIAA Aviation Technology, Integration, and Operations (ATIO) Conference and 14th AIAA/ISSM, 2012.

[6] 裴曉強, 黃海.協同優化在衛星多學科設計優化中的初步應用[J].宇航學報, 2006, 27(5): 1054-1058.(Pei Xiaoqiang, Huang Hai. Multidisciplinary Design Optimization of Satellites Using Collaborative Optimization [J]. Journal of Astronautics, 2006, 27(5): 1054-1058.)

[7] 洪煌杰, 王紅巖, 郝貴祥. 基于響應面法的空降車緩沖氣囊參數優化研究[J].系統仿真學報, 2013, 25(2): 327-332.(Hong Huangjie, Wang Hongyan, Hao Guixiang. Research on Parameter Optimization of Airbags for Airborne Vehicle Base on Response Surface Methodology [J]. Journal of System Simulation, 2013, 25(2): 327-332.)[8] 孫奕捷, 申功璋.飛行器多學科設計優化中迭代更新的近似模型生成方法[J]. 航天控制, 2009, 27(5): 58-64.(Sun Yijie, Shen Gongzhang. Iteratively Updating Method of Generating Approximation Model in Multidisciplinary Design Optimization [J]. Aerospace Control, 2009, 27(5): 58-64.)

[9] 夏昊, 諸成, 陳昌亞, 等.基于近似模型的衛星動力學多目標優化[J].上海航天, 2013, 30(5): 48-53.(Xia Hao, Zhu Cheng, Chen Changya, et al. Dynamic multi-objective optimization of satellite based on approximation models[J].Aerospace Shanghai, 2013, 30(5): 48-53.)

[10] 蔣平, 匡玲, 邵新宇, 等.基于近似模型的兩級集成系統協同優化方法[J].中國機械工程, 2012, 23(4): 395-401.(Jiang Ping, Kuang Ling, Shao Xinyu, et al. A New BLISCO Method Based on Approximate Models [J]. China Mechanical Engineering, 2012, 23(4): 395-401.)

A Collaborative Optimization Method Based on Response Surface Update Approach for Aircraft System

Chi Yuancheng, Wang Yanjing, Dong Wei, Lu Xiaobing, Guo Huizhang

Research & Development Center of China Academy of Vehicle Technology, Beijing 100076, China

Manycomplexproblemsareconfrontedintheaircraftsystemdesign,involvingmanydifferentsubsystemswhicharehighlycoupled.Byconsideringthedemandofaircraftsystemdesignoptimization,acollaborativeoptimizationbasedonresponsesurfaceupdateapproachisproposed.ThisoptimalsolutionisusedintheapproachasnewcomplementarytrainingsampletoupdateapproximationmodelandtheCOisappliedtothesystemdesignoptimization.Theresultsofexamplesshowthisapproachisfasttoobtainoptimalsolutionforaircraftsystemdesign.

Aircraftsystemdesign;Collaborativeoptimization;Responsesurfacemethodology;Designofexperiment

2015-07-29

池元成(1981-)，男，黑龍江寧安人，博士，工程師，主要研究方向為飛行器多學科設計與優化；王彥靜(1984-)，女，河北邯鄲人，碩士，工程師，主要研究方向為數字化設計；董 偉(1971-)，男，武漢人，碩士，高級工程師，主要研究方向為項目管理與協同優化；陸小兵(1985-)，男，安徽樅陽人，碩士，工程師，主要研究方向為數字化設計；郭會章(1979-)，男，遼寧盤錦人，碩士，工程師，主要研究方向為數字化設計。

TP301；V21

A

1006-3242(2016)02-0076-04