航天器燃料最優編隊機動控制的解析方法

龔德仁 陳吉安 段登平 陳昌亞

1.上海交通大學，上海 200240 2.上海衛星工程研究所，上海 200240

?

航天器燃料最優編隊機動控制的解析方法

龔德仁1陳吉安1段登平1陳昌亞2

1.上海交通大學，上海 200240 2.上海衛星工程研究所，上海 200240

針對航天器燃料最優編隊初始化、重構等機動展開研究，提出了一種解析控制方法。首先將編隊機動問題從狀態空間轉換到構型參數空間進行分析，其次基于不等式約束分別得到軌道平面內、外運動的燃料消耗下界，進一步獲得燃料最優時需要滿足的條件和可行的燃料最優編隊機動解析解，該解形式簡單，計算量小。燃料消耗量取決于相對運動尺寸參數，而最優解的存在性取決于初始狀態誤差。數值仿真結果驗證了所提方法的有效性和準確性。 關鍵詞 航天器編隊飛行；燃料最優機動；構型參數化；解析解

航天器編隊飛行具有成本低、系統可靠性高和適應性強等優點，已成為空間分布式任務研究中的熱點[1]。由于衛星攜帶燃料有限，上天后無法得到及時補充，因此在編隊機動過程中如何節省燃料非常重要，且已被廣泛關注[2]。現有的燃料優化方法可以分成2類：1)基于線性化的運動狀態模型；2)基于軌道根數差。

基于線性化運動狀態模型的燃料優化編隊機動一般采用Clohessy-Wiltshire方程[3]、Lawden方程[4]和Tschauner-Hempel方程[5]。優化方法包括線性規劃算法[6-7]、遺傳算法[8]、進化算法[9]、Hamilton-Jacobian-Bellman優化方法[10-11]、主矢量算法[12-13]、線性/非線性混合優化[14]和高斯偽譜法[15-16]等。其它的研究包括編隊重構的可達性與最優相位分析[17]、編隊最優制導設計[18]和考慮復雜攝動的繞飛控制策略[19]等。

基于軌道根數差的編隊機動控制方法采用Gauss軌道攝動模型和軌道根數差相對運動學方程，主要包括解析的雙脈沖控制方法[20-21]，三沖量方法[22]，基于燃料當量分析的編隊機動制導方法[23]，近優反饋控制方法[24]和小推力燃料優化機動控制方法[25]等。

總體來說，針對燃料最優編隊機動問題，已有研究多采用數值方法進行求解，或者在脈沖次數固定情況下獲得解析的脈沖值。數值方法并不能得到真正意義上的最優解，且計算量大，不具有普遍意義；脈沖次數限制則增加了約束條件，使最優解可能被排除在外，況且最優解既有可能是脈沖推力，也有可能是連續推力，或者理論上就不存在。

本文在構型參數空間中展開研究，分析燃料下界及其可達性，由此得到燃料最優的條件和可行的解析解，并分析了各種初始條件下最優解的存在性、推力是脈沖的還是連續的。采用數值方法對交會過程和水平投影圓編隊機動進行仿真，驗證了理論分析的正確性。

1 問題描述

航天器之間的相對運動關系一般在主航天器軌道坐標系中描述，一階近似模型為Clohessy-Wiltshire方程。假設航天器能提供3個軸向的推力，這時燃料消耗與控制力的1-范數成正比，燃料最優編隊機動可以寫成

(1)

其中：J為燃料消耗量，ΔX0為初始狀態誤差；tf為機動時間；U(t)=[ux(t),uy(t),uz(t)]T為控制力向量，脈沖控制時為δ函數的級數；Φ(t)為Clohessy-Wiltshire方程的狀態轉移矩陣，

(2)

其中，n為主航天器的平均軌道角速度。

定義構型參數P=[p,φ,s,l,q,θ]T如下：

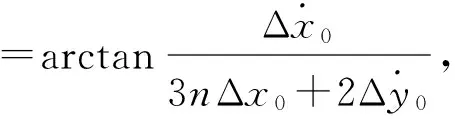
(3)

其中：p,q,s和l為尺寸參數，φ和θ∈[0, 2π)為相位參數。

采用構型參數P表示的誤差向量ΔX(t)為

Δx(t)=-pcos(nt+φ)+s,

Δy(t)=2psin(nt+φ)+l-1.5nts,

Δz(t)=qsin(nt+θ),

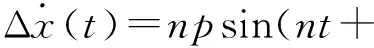
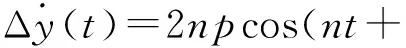
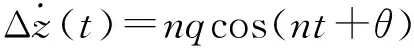
(4)

顯然，參數p和φ表示軌道平面內運動的尺寸和相位，s和l表示軌道平面內運動的中心偏移，q和θ表示軌道平面外運動的尺寸和相位。

根據初始誤差狀態ΔX0和構型參數P之間的關系，優化問題式(1)可以整理為

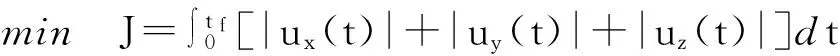
(5)

2 問題求解

定理 對于區間[0,tf],tf≥0上任意的實可積函數f(t)和g(t)，不等式

(6)

恒成立。

證明：定義平面曲線L為

(7)

顯然，初始點L(0)=(0, 0)就是坐標原點O，如圖1所示。

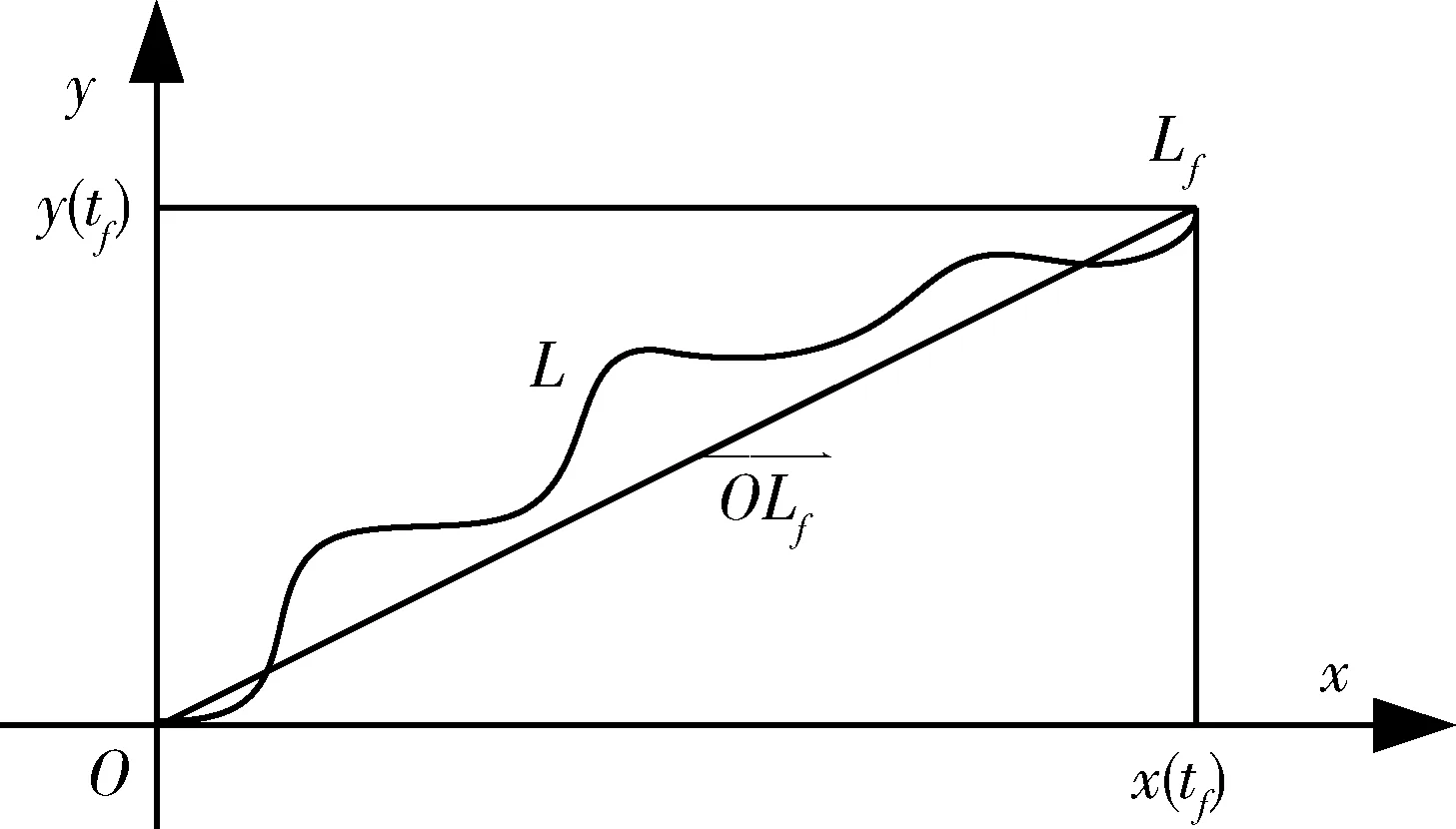
圖1 曲線L示意圖

(8)

其中，(·)′表示對變量t的導數。在平面Oxy內，連接點O和點Lf之間任意曲線的長度都大于直線OLf的長度

h2≥|OLf|2=x2(tf)+y2(tf)

(9)

其中，Lf=L(tf)是曲線L的終點。將式(7)和式(8)代入式(9)可得

(10)

當式(10)中的等號成立時，曲線L(t)變成直線OLf，此時滿足

f(t)x(tf)≥0;g(t)y(tf)≥0

(11)

其中，κ(t)為曲線L的斜率。式(11)表明終點Lf決定了滿足式(10)的曲線L的性質。

2.1 軌道平面外運動

根據方程式(5)可知，軌道平面外運動的最優機動為

(12)

根據不等式(6)可知燃料消耗Jz滿足

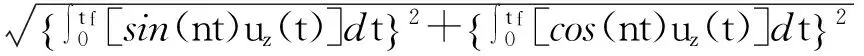
=nq

(13)

因此，nq是Jz的一個下界。僅當下列條件

(14)

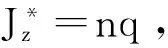
(15)

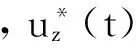
(16)

式(16)為優化問題式(12)的解析解。可知最優解不存在連續推力，只能是脈沖序列。最少僅需一次脈沖，如在t=T-Tθ時刻施加正向脈沖nq，或在t=1.5T-Tθ時刻施加負向脈沖-nq。

2.2 軌道平面內運動

根據式(5)可知，軌道平面內最優機動可以描述成

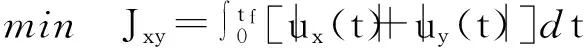
(17)

根據式(17)的前2個約束可得

(18)

因此，0.5np是燃料消耗Jxy的一個下界。當Jxy=0.5np時，燃料達到最小值，控制力需滿足

(19)

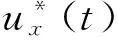
(20)

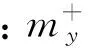
(21)

上式表明Jxy有第2個下界，此時控制力滿足

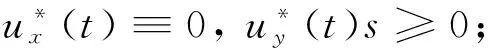
(22)

也就是徑向控制力為0，切向控制力始終為正或負，取決于初始構型中心偏移參數s。

綜合前面的討論可知，軌道平面內的燃料消耗Jxy滿足

(23)

下面針對3種不同情況分別進行討論。

Case1:p=|s|=0,l≠0

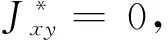
uy(1)=-uy(2)=-l/(3kT),t2=t1+kT;k∈Z+

(24)

此時燃料消耗為

Jxy=2|l|/(3kT)

(25)

Case2:p>|s|

由式(23)可知，此時最小燃料為0.5np。將式(19)代入式(17)中的其它約束,可得最優解滿足

(26)

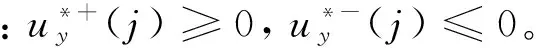
由于式(26)中對脈沖大小有3個等式約束，因此最少三脈沖就可以實現。不妨令2次為負脈沖，1次為正脈沖，此時可得

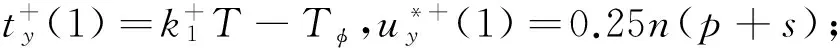
(27)

其中：α∈[0, 1]，且滿足

(28)

式(28)可稱為p>|s|時最優三脈沖編隊機動的基本方程，其解為：

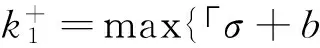
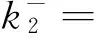
(29)

Case3:p≤|s|

(30)

根據后2個等式約束，則sl≤0時不存在最優解，只能進行次優控制。

針對式(30)前3個約束，定義平面曲線S如下

(31)

這里滿足uy(t)s≥0。曲線S的起點為坐標原點O，終點Sf的坐標為(0.5npcosφ, -0.5npsinφ)，如圖2所示。

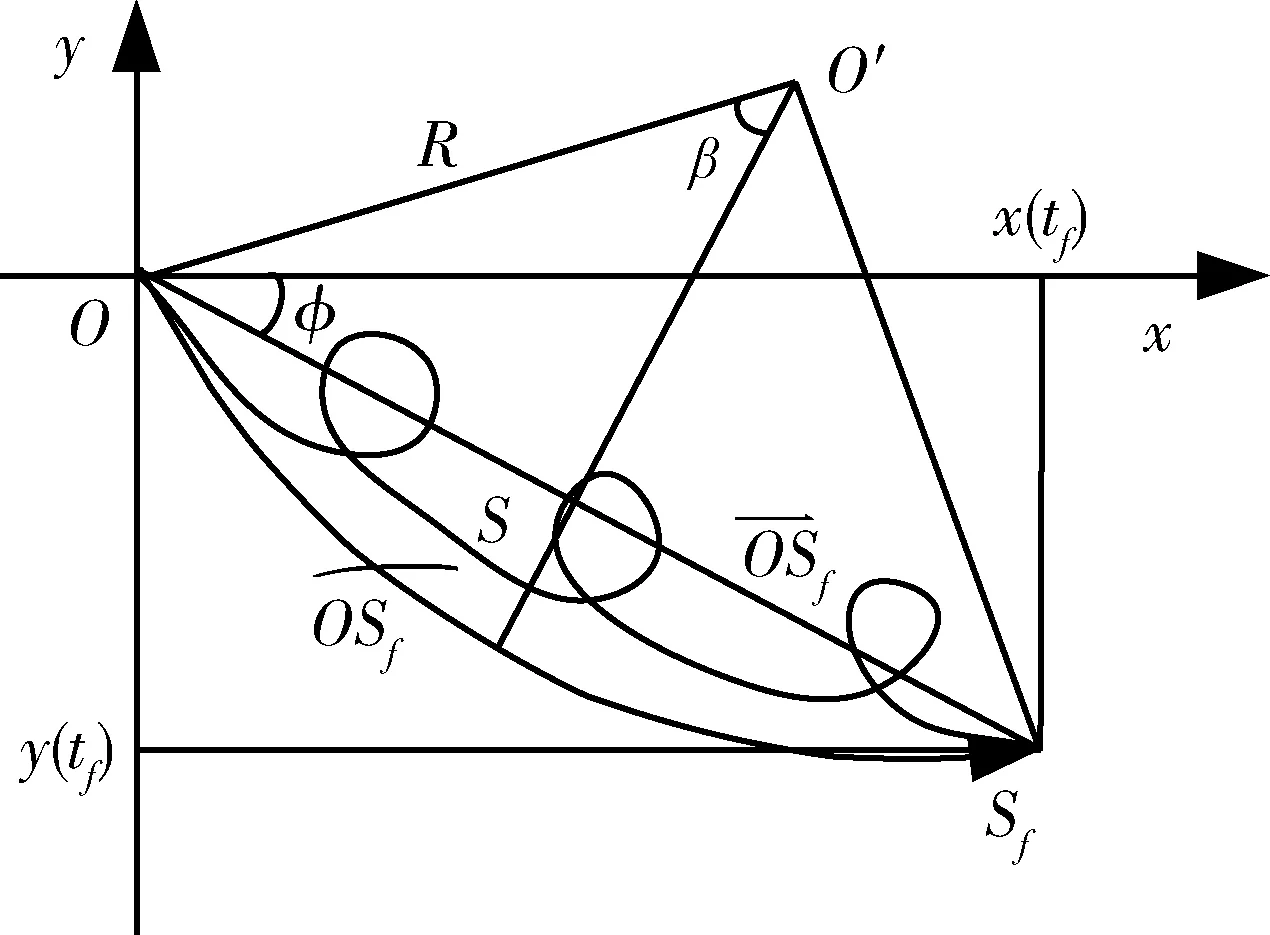
圖2 曲線S示意圖

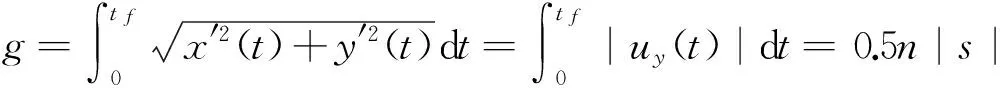
(32)

定義推力uy(t)與時間t乘積的積分為推力影響

(33)

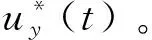
進一步可知，曲線的斜率κ(t)和曲率半徑ρ(t)分別為

(34)

可知κ(t)僅與時間相關，ρ(t)為控制力的1/n。

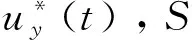
β=sinc-1(p/|s|)≥0,R=0.25n|s|/β

(35)

其中：R和β分別為圓的半徑和半圓心角，sinc(x)=sin(x)/x。

根據式(34)和(35)可知，最優控制力為

(36)

其中

(37)

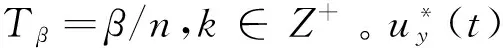
(38)

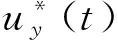
對于編隊機動(s,p)，令兩段推力產生的效果分別為(s1,p1)和(s2,p2)

(39)

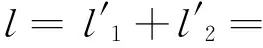
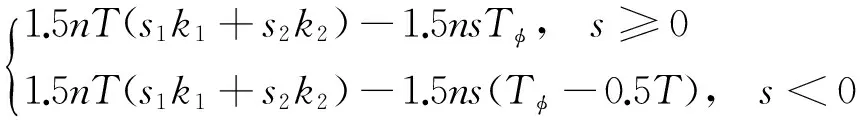
因此有

(41)

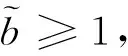
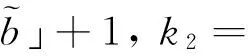
(42)

考慮到約束|s1|≥p1，|s2|≥p2和ε,η∈[0,1]，因此η的范圍為

(43)

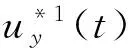
此外，也可以采用脈沖推力實現編隊機動。假設脈沖時刻為

(44)

其中：kj∈Z+，my為脈沖次數，上標“o”和“e”分別表示kj為奇數和偶數時的脈沖。由式(30)可得

(45)

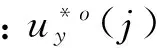
(46)

比較式(46)和式(26)的形式可知，兩者僅僅變量不同，可以采用相同方法進行求解。

當sl≤0時，最優解不存在，只存在次優解。一種策略就是分2次進行控制，第1次將p，φ和s控制為0，第2次將l控制為0。總體上是一種次優控制策略，因為將l控制為0所需的燃料隨著時間的增加呈反比例下降。

3 仿真示例

3.1 交會過程

假設目標航天器運行在800km高的近圓軌道上，軌道周期為T=6052.4s，追蹤航天器位于目標航天器后方3000m、下方100m的軌道上。初始時刻的構型參數為

P=[0m, 0°, 100m, 3000m, 0m, 0°]T

可知交會過程符合p≤|s|，且sl>0的情況。根據前面的分析結果可知，采用連續推力和脈沖推力兩種方式都可以實現最優機動。

采用連續推力控制，最優控制力為

總燃料消耗為

采用脈沖推力控制，一種最優脈沖序列為

t(1)=to(1)=0.5T,

t(2)=to(2)=1.5T,

t(3)=te=5T,

燃料消耗為

仿真結果如圖3所示，2種機動方式都是燃料最優的。

3.2 水平投影圓編隊機動

水平投影圓編隊是指輔航天器圍繞主航天器飛行，其繞飛軌跡在當地水平面內投影為圓形的編隊。該編隊構型可以用圓的半徑R和初始相位γ來描述。從一個水平圓構型(R0,γ0)到另一個水平圓構型(Rd,γd)進行機動時，相對構型參數為

P=[0.5R,γ, 0, 0,R,γ+0.5π]T。

其中，

根據前面分析可知軌道平面外采用一次脈沖

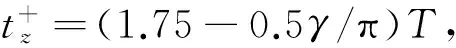
軌道平面內采用3次脈沖就可以實現燃料最優編隊機動

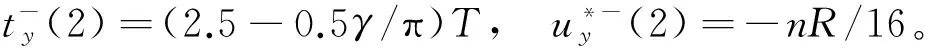
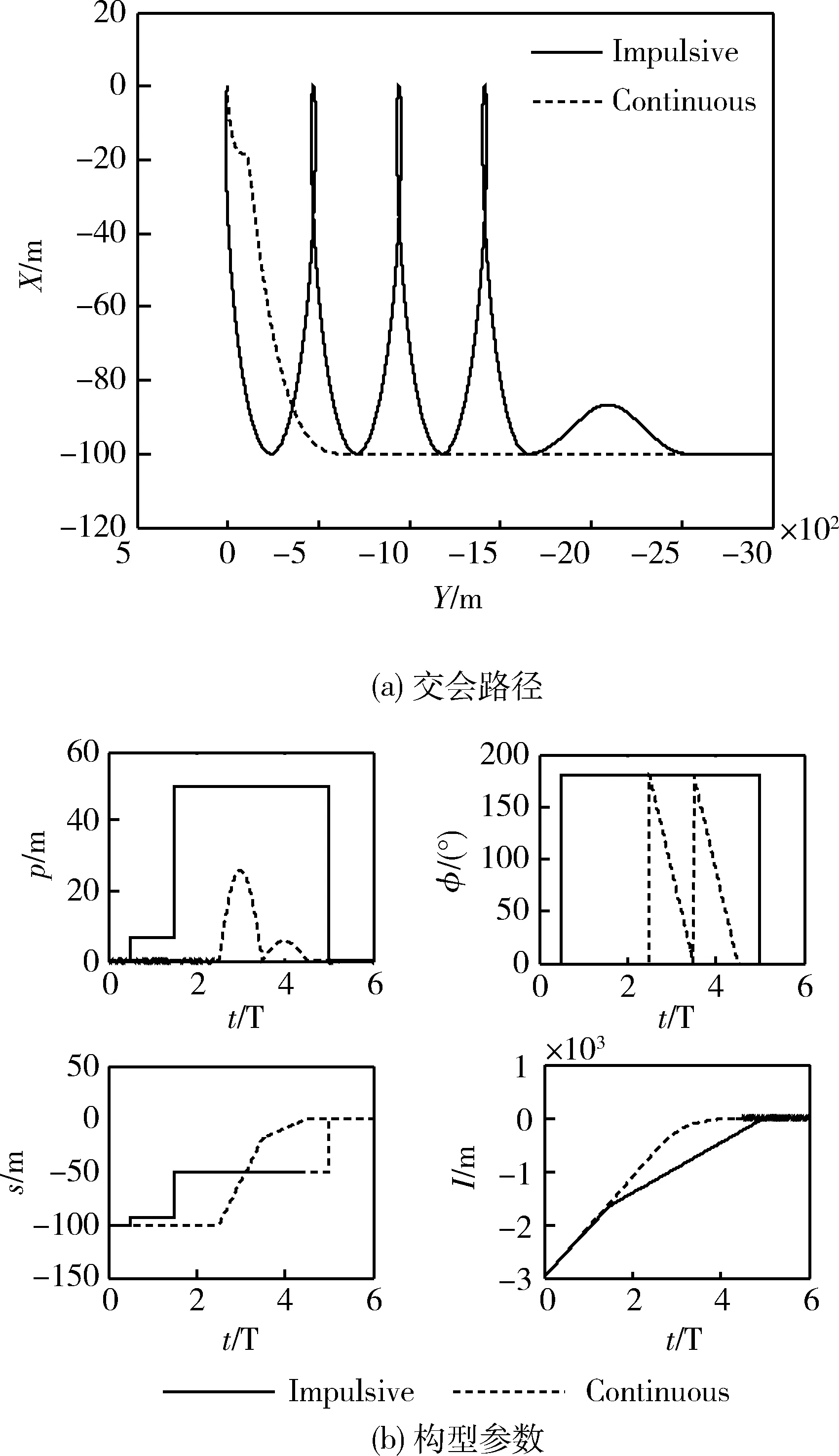
圖3 燃料最優交會

仿真結果如圖4所示，相位參數φ和θ保持不變，脈沖施加時刻滿足Δx(t)=0或Δz(t)=0。

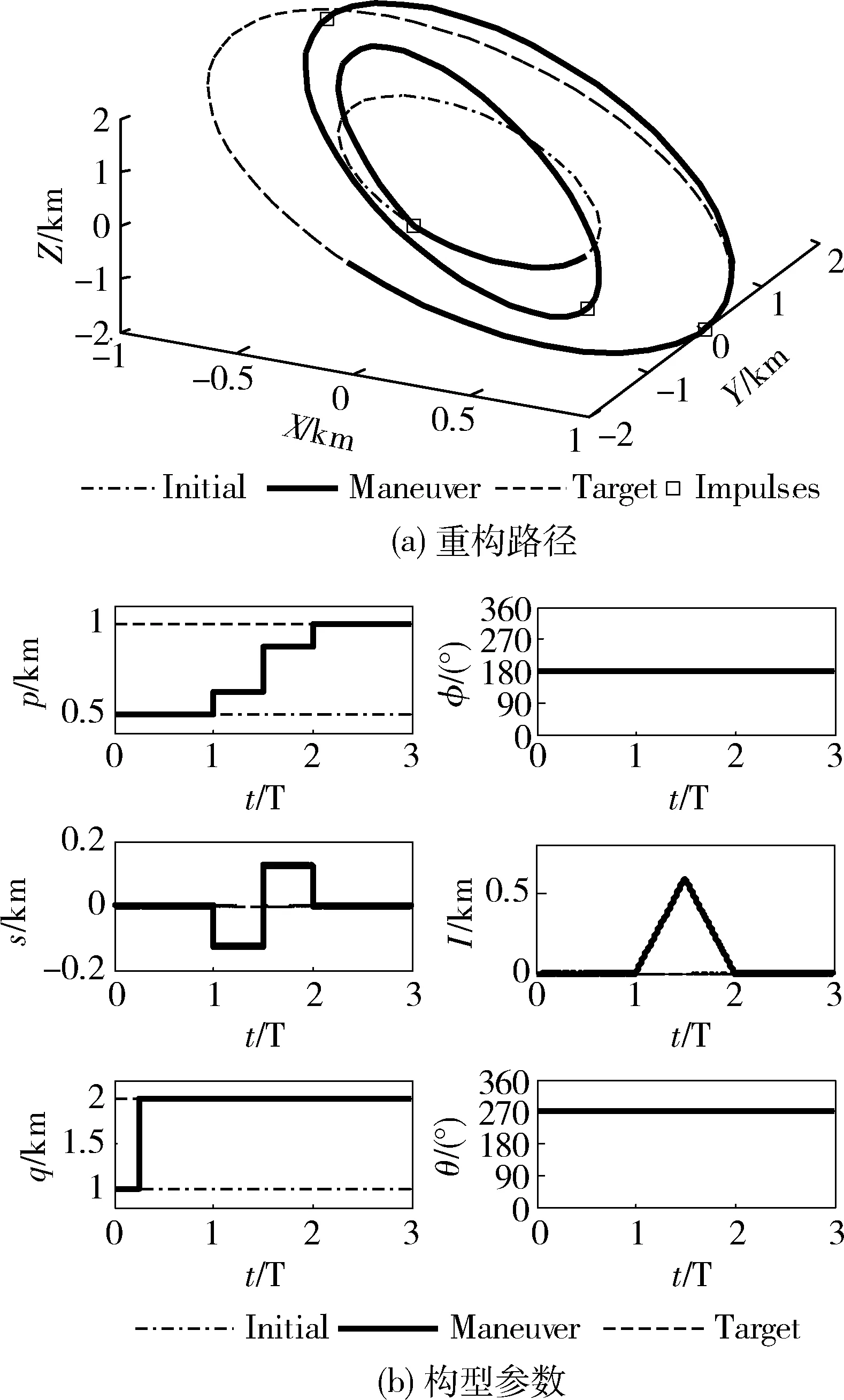
圖4 燃料最優編隊機動

4 結論

針對燃料最優編隊機動控制，采用構型參數空間分析方法得到了解析解。結果表明，燃料最優解的存在性與初始條件有關，最優解只要存在就有多種，燃料消耗與相對尺寸參數有關。該解析控制方法不僅可以用在編隊機動上，同時也可用在航天器交會過程中。

[1]ScharfDP,HadaeghFY，PloenSR.Asurveyofspacecraftformationflyingguidanceandcontrol(part1):guidance[C].Proc.ofthe2003AmericanControlConference,Dayton,Ohio,June2003: 1733-1739.

[2]IchimuraY，IchikawaA.Optimalimpulsiverelativeorbittransferalongacircularorbit[J].JournalofGuidanceControlandDynamics, 2008, 31(4): 1014-1027.

[3]ClohessyWH,WiltshireRS.Terminalguidancesystemforsatelliterendezvous[J].JournalofAerospaceSciences, 1960, 27(9): 653-658.

[4]LawdenD.Fundamentalsofspacenavigation[J].JournaloftheBritishInterplanetarySociety, 1954, 13(2): 87-101.

[5]TschaunerJ.Ellipticorbitrendezvous[J].AIAAJournal, 1967, 5(6): 1110-1113.

[6]TillersonM,InalhanG,HowJP.Co-ordinationandcontrolofdistributedspacecraftsystemsusingconvexoptimizationtechniques[J].InternationalJournalofRobustandNonlinearControl, 2002, 12(2): 207-242.

[7]UmeharaH,McInnesCR.Fuel-optimumnear-missavoidancecontrolforclusteredsatellites[C].Proc.ofthe18thnternationalSymposiumonSpaceFlightDynamics,Munich,Germany, 2004.

[8]YangG,YangQS,KapilaV,PalmerD.Fueloptimalmaneuversformultiplespacecraftformationreconfigurationusingmulti-agentoptimization[C].Proc.ofthe40thIEEEConferenceonDecisionandControl, 2001: 1083-1088.

[9]WangS,ZhengC,WangY.Atime-fueloptimalforspacecraftformationreconfiguration[C].Proc.ofIEEECongressonEvolutionaryComputation, 2007: 994-998.

[10]CampbellME.Planningalgorithmforlargesatelliteclusters[J].JournalofGuidance,Control,andDynamics, 2003, 26(5): 770-780.

[11]ZanonDJ,CampbellME.Optimalplannerforspacecraftformationsinellipticalorbits[J].JournalofGuidance,Control,andDynamics, 2006, 29(1): 161-171.

[12]MailheLM,GuzmanJJ.Initializationandresizingofformationflyingusingglobalandlocaloptimizationmethods[C].Proc.ofIEEEAerospaceConf.,BigSky,Montana,March6-14, 2004: 547-556.

[13]KimDY,WooB,ParkSY,ChoiKH.Hybridoptimizationformultiple-impulsereconfigurationtrajectoriesofsatelliteformationflying[J].AdvancesinSpaceResearch, 2009, 44(11): 1257-1269.

[14]KumarBS,NgA.Time-optimallow-thrustformationmaneuveringusingahybridlinear/nonlinearcontroller[J].JournalofGuidanceControlandDynamics, 2009, 32(1): 343-347.

[15] 趙宇, 趙洪華. 橢圓軌道衛星編隊燃料最優機動實時算法[J]. 中國空間科學技術, 2009, 29(5): 33-41. (ZhaoYu,ZhaoHonghua.Real-timeAlgorithmforFormationSatelliteFuel-optimalManeuversinEllipticOrbits[J].ChineseSpaceScienceandTechnology, 2009, 29(5): 33-41.)

[16] 董曉光, 曹喜濱, 張錦繡, 等.編隊飛行最優相對軌跡生成與跟蹤控制[J].系統工程與電子技術, 2013, 35(1): 138-145. (DongXiaoguang,CaoXibin,ZhangJinxiu,etal.Optimalrelativetrajectorygenerationandtrackingcontrolofformationflying[J].SystemsEngineeringandElectronics, 2013, 35(1): 138-145.)

[17]PalmerP.Reachabilityandoptimalphasingforreconfigurationinnear-circularorbitformations[J].JournalofGuidanceControlandDynamics, 2007, 30(5): 1542-1546.

[18]HughesSP.Generalmethodforoptimalguidanceofspacecraftformations[J].JournalofGuidanceControlandDynamics, 2008, 31(2): 414-423.

[19] 姜宇, 李恒年, 潘立公，等.衛星編隊飛行相對繞飛控制策略[J].航天控制, 2014, 32(1): 55-62. (JiangYu,Lihengnian,PanLigong,etal.Relativefly-aroundcontrolstrategyforsatelliteformationflying[J].AerospaceControl, 2014, 32(1): 55-62.)

[20]VaddiSS,AlfriendKT,VadaliSR,SenguptaP.Formationestablishmentandreconfigurationusingimpulsivecontrol[J].JournalofGuidanceControlandDynamics, 2005, 28 (2): 262-268.

[21]SchaubH,AlfriendKT.ImpulsiveFeedbackcontroltoestablishspecificmeanorbitelementsofspacecraftformations[J].JournalofGuidance,Control,andDynamics, 2001, 24(4): 739-745.

[22] 姚紅, 曾國強, 胡敏. 基于相對軌道根數的航天器編隊控制三沖量方法[J].航天控制, 2009, 27(6): 46-51.(YaoHong,ZengGuoqiang,HuMin.Three-impulsemethodforformationcontrolofspacecraftbasedonrelativeorbitelements[J].AerospaceControl, 2009, 27(6): 46-51.)

[23]HamelJF,LafontaineJD.Fuel-equivalentrelativeorbitelementspace[J].JournalofGuidanceControlandDynamics, 2008, 31(1): 238-244.

[24]HuntingtonGT,RaoAV.OptimalreconfigurationofspacecraftformationsusingtheGausspseudospectralmethod[J].JournalofGuidanceControlandDynamics, 2008, 31(3): 689-698.

[25]WuBL,WangDW,PohEK,XuGY.Nonlinearoptimizationoflow-thrusttrajectoryforsatelliteformation:Legendrepseudospectralapproach[J].JournalofGuidanceControlandDynamics, 2009, 32(4): 1371-1381.

Analytical Solutions to Fuel-Optimal Spacecraft Formation Maneuver

Gong Deren1, Chen Ji’an1, Duan Dengping1, Chen Changya2

1.Shanghai Jiao Tong University, Shanghai 200240, China 2.Shanghai Institute of Satellite Engineering, Shanghai 200240, China

Anewsimplemethodisproposedforfuel-optimalspacecraftformationmaneuver,includinginitializationandreconfiguration,andanalyticalsolutionswithoptimal/suboptimalstrategiesareobtained.Themethodconsistsoftwostages.Firstly，anewformofparameterizationofformationmaneuverstateisdevelopedforsimplicity.Secondly,theout-of-planeandin-planemotionareseparatelystudiedastheyareuncoupled.Withthehelpofausefulinequalityintroducedandproved,thelowerboundofthefuelconsumptionandthecorrespondingconstraintsofthecontrolforcesarederivedandobtained.Theresultsshowthattheminimumtotalfuelconsumptiondependsontherelativesizeparametersandtheexistenceofoptimalcontrolalgorithmdependsupontheinitialconditions.Thenumericalsimulationsofthetwoapplicationsareproventhatthetheproposedmethodisvalideandefficient.

Spacecraft-formationflying;Fuel-optimalmaneuver;Configurationparameters;Parameterization;Analyticalsolutions

2014-10-29

龔德仁(1982-)，男，湖南婁底人，講師，主要從事分布式衛星系統姿軌協同和相對導航控制研究；陳吉安(1965-)，男，吉林四平人，教授，博士生導師，主要從事飛行器結構和力學研究；段登平(1966-)，男，重慶銅梁人，教授，博士生導師，主要從事空間飛行器總體設計與研制；陳昌亞(1963-)，男，安徽安慶人，研究員，主要從事航天器總體設計和深空探測技術研究。

V448.22+4

A

1006-3242(2016)01-0037-08