基于響應曲面法的煤油發動機氣門正時優化

張　偉　毛建國　魏特特　何小明

南京航空航天大學，南京，210016

?

基于響應曲面法的煤油發動機氣門正時優化

張偉毛建國魏特特何小明

南京航空航天大學，南京，210016

利用基于仿真的響應曲面優化方法，對改型的煤油活塞發動機氣門正時多目標優化問題進行了研究。建立了發動機性能仿真模型，以進氣/排氣正時、點火提前角為優化變量，以提高有效功率和降低燃油消耗率為設計目標進行了響應曲面優化。分析結果表明：相對于原汽油機，改型的煤油機進氣門開啟時刻要推遲，排氣門關閉時刻要遲后，并且要提前一定的點火提前角，以得到最佳的發動機性能；同時，應用響應曲面法可以提升仿真優化的效率。

煤油發動機；數值模擬；響應曲面法；正時

0　引言

煤油在理化性質上，相比于汽油，具有閃點高、不易揮發的性質，而且密度比柴油小，同等質量下體積更小，所以其在安全、后勤保障方面有著重要地位[1]，以煤油為燃料的活塞發動機已成為研究熱點。國內煤油活塞發動機起步較晚，正處于理論探索階段，研究大多是在改型的汽機油的基礎上進行的[2]。因此，在發動機的各個層面還需要根據煤油的特性進行改進設計、匹配優化。由于煤油具有燃燒速率比汽油低、不易蒸發等特點，其燃燒過程與汽油有很大不同，所以需要重新設計與之相匹配的換氣過程，即需要對配氣相位進行計算分析。

許多學者進行了發動機配氣相位優化的相關工作，但大多是針對汽油、柴油機的，且優化方法上多是利用一般的配湊或直接法進行優化，優化方法不易實施且耗費很多計算時間。文獻[3-5]將氣門優化轉化為單目標優化問題，而優化時僅由經驗在仿真模型上試湊設計變量，優化結果受主觀影響，且單目標無法考慮各個優化變量間的相互作用；文獻[6-7]將仿真模型與優化算法直接耦合對配氣相位進行優化，雖然可以得到準確的最優解，但耗費了大量的仿真計算時間；文獻[8-10]采用DoE方法實現了對進排氣參數的優化，但沒有進一步結合響應曲面擬合算法，仍需要進行較多的仿真試驗。

本文以某改型的煤油活塞發動機為研究對象，采用基于仿真的響應曲面優化方法對原氣門正時進行了優化，改善了改型發動機的性能，同時將響應曲面法應用于優化中，提高了仿真優化的效率。

1　響應曲面法

響應曲面法(response surface methodology)是一種綜合了統計學和數學并適用于產品開發、改進設計、優化處理的方法，最初應用于化學生產加工。隨著其發展，響應曲面法被引入基于計算機仿真模型的優化中，利用響應曲面法建立仿真模型的近似模型，即元模型(metamodel)，然后在元模型上進行優化分析[11]。

響應曲面可以用下式表示：

y=f(β1,β2,…,βn,x1,x2,…,xk)+ε

(1)

式中，y為目標函數；xi(i=1,2,…,k)為設計變量；f為響應曲面模型，一般為多項式；ε為系統誤差；βj(j=1,2,…,n)為未知參數。

建立響應曲面的過程就是利用回歸分析方法對未知參數β進行估計的過程。

雖然直接利用高精度仿真模型進行優化可以獲得準確可靠的優化方案，然而，當仿真模型十分復雜時，每次仿真計算都需要很長的計算時間，而且一次優化分析又需要調用數次仿真計算，耗費了大量時間資源。相對于一般的優化方法，響應曲面法可以反映設計參數和目標函數之間的關系。在充足的數據點和高精度回歸方法的支持下，通過代數表達式可以形象地描繪出設計參數對目標函數的響應，因此在實際優化問題中，響應曲面法可以簡化實際的復雜仿真模型，在保證必要精度的前提下，節省大量的仿真計算消耗，并能夠完成優化任務[12]。

通常，基于仿真的響應曲面優化策略流程如圖1所示。首先，選擇試驗設計，即由設計空間中較小數量的數據點實現獲取信息最大化的方法[13]，得到一組具有代表性的初始設計點，并調用仿真模型計算這些設計點。然后對上述數據點進行統計分析，為特定的優化問題建立仿真模型的元模型[14-15]，即優化變量與目標變量的響應曲面。再驗證所建立的響應曲面的有效性，如果精度不滿足要求，則重新進行試驗設計。得到可靠的響應曲面之后，就可以在響應曲面上利用優化算法搜尋最優解。最后將選定的最優解代入仿真模型進行評估[16]。

圖1　基于仿真的響應曲面優化策略流程圖

2　原型機GT-Power仿真模型

本文以某改型的進氣道噴射四沖程煤油活塞發動機為研究對象(主要技術參數如表1所示，其中單位“°”表示曲軸轉角)，利用一維CFD仿真軟件GT-Power建立了該發動機的性能仿真模型，如圖2所示。考慮氣缸幾何形狀、混合氣運動、燃料特性以及便于點火提前角調整，燃燒模型選取EngCylCombSITurb模型；為反映進氣道噴射燃料在氣道的積累、蒸發和向氣缸傳遞的過程，進氣道、排氣道選取PipePort模型。

表1　原型機主要技術參數

圖2　原型機GT-Power模型

通過對比實驗測取的不同轉速(3000～5000 r/min)下，節氣門開度為20%時的原型機缸內壓力曲線，驗證原型機GT-Power模型的有效性。

本文選取發動機轉速為5000 r/min時的缸內壓力對比曲線為例，如圖3所示，仿真值曲線和實驗值曲線基本吻合，燃燒段誤差已遠小于5%，達到了工程允許的誤差范圍，該模型可以用于原型機的仿真、優化任務。

圖3　5000 r/min時的缸內壓力對比

3　基于響應曲面法的氣門正時優化

本文采用基于仿真的響應曲面優化策略，借助專業優化軟件modeFRONTIER(簡稱MF)，將其與GT-Power仿真模型耦合，在不改變進氣門、排氣門開啟持續期的情況下，以進氣提前角、排氣遲閉角以及點火提前角(均指曲軸轉角)為設計變量，以有效功率最大化、有效燃油消耗率最小化為目標進行優化。

3.1建立MF優化模型

整個優化策略的實現依托于在MF中建立的優化模型，如圖4所示。

圖4　MF優化模型

MF優化模型包括：①輸入參數，即設計變量進氣正時、排氣正時、點火提前角，以及常量轉速，因為原型機常用轉速在4000～5000 r/min之間，所以優化時將轉速恒定在4500 r/min；②輸出參數，即優化目標有效功率、有效燃油消耗率以及相應的約束條件；③MF與GT-Power耦合的節點，以實現MF對GT-Power進行仿真計算的調度以及優化參數和仿真數據的傳輸；④邏輯調度節點，用于定義試驗設計和優化調度算法，以確定優化計算分析的過程。優化模型中優化參數的邊界及約束條件設置見表2。

表2　優化參數邊界及約束條件的設置

3.2由試驗設計生成初始數據點

建立基于仿真的響應曲面需要提供仿真模型的一系列具有代表性的仿真數據點，響應曲面的精度與這些仿真數據點的分布密切相關。因此，如何布置數據點對建立響應曲面至關重要[17]，即合適的試驗設計是建立響應曲面的基礎。相關學者提出了許多試驗設計方法[11]，本文運用均勻拉丁超立方[18](uniform latin hypercube，ULH)方法進行試驗設計，為響應曲面的建立提供初始數據點。ULH是一種常用的十分適用于仿真模型的空間填充技術(space-filling design)，可以在設計變量空間中生成分布相對均勻的數據點。對于n個設計點，k個變量的ULH，可以看成一個n×k的矩陣。每個變量Xi服從在其上下邊界內的均勻分布，而矩陣的每一列相當于n個Xi的隨機排列。

通常，仿真模型需要用二階響應曲面模型簡化。將k個設計變量的二階響應曲面函數在點(x10，x20，…，xk0)處按泰勒級數展開，可以按x的冪次整理成如下形式：

(2)

式中，ε為系統誤差；β為泰勒展開式中各項合并后的未知常數項。

由式(2)可以明確地看出其中包含1+2k+k(k-1)/2個未知參數β。因此，確定試驗設計設計點的基本原則為必須至少有1+2k+k(k-1)/2個設計點；同時，設計中每個設計變量至少需要3個水平，以估計純二次項[11]。本文有3個設計變量，所以需要生成33=27個初始設計點，圖5所示為由ULH生成的設計變量空間。

圖5　ULH生成的設計變量空間

對以上設計點執行仿真計算，最終得到建立響應曲面所需的初始仿真數據。

3.3響應曲面的建立

由試驗設計得到的一組涵蓋仿真模型信息的數據點，利用回歸分析方法可以建立起所需的響應曲面模型。徑向基函數法(radial basis functions, RBF)是一種常用的回歸分析方法，可以較好地由ULH得到的數據點建立關于配氣正時的響應曲面。RBF適于多個離散變量插值。

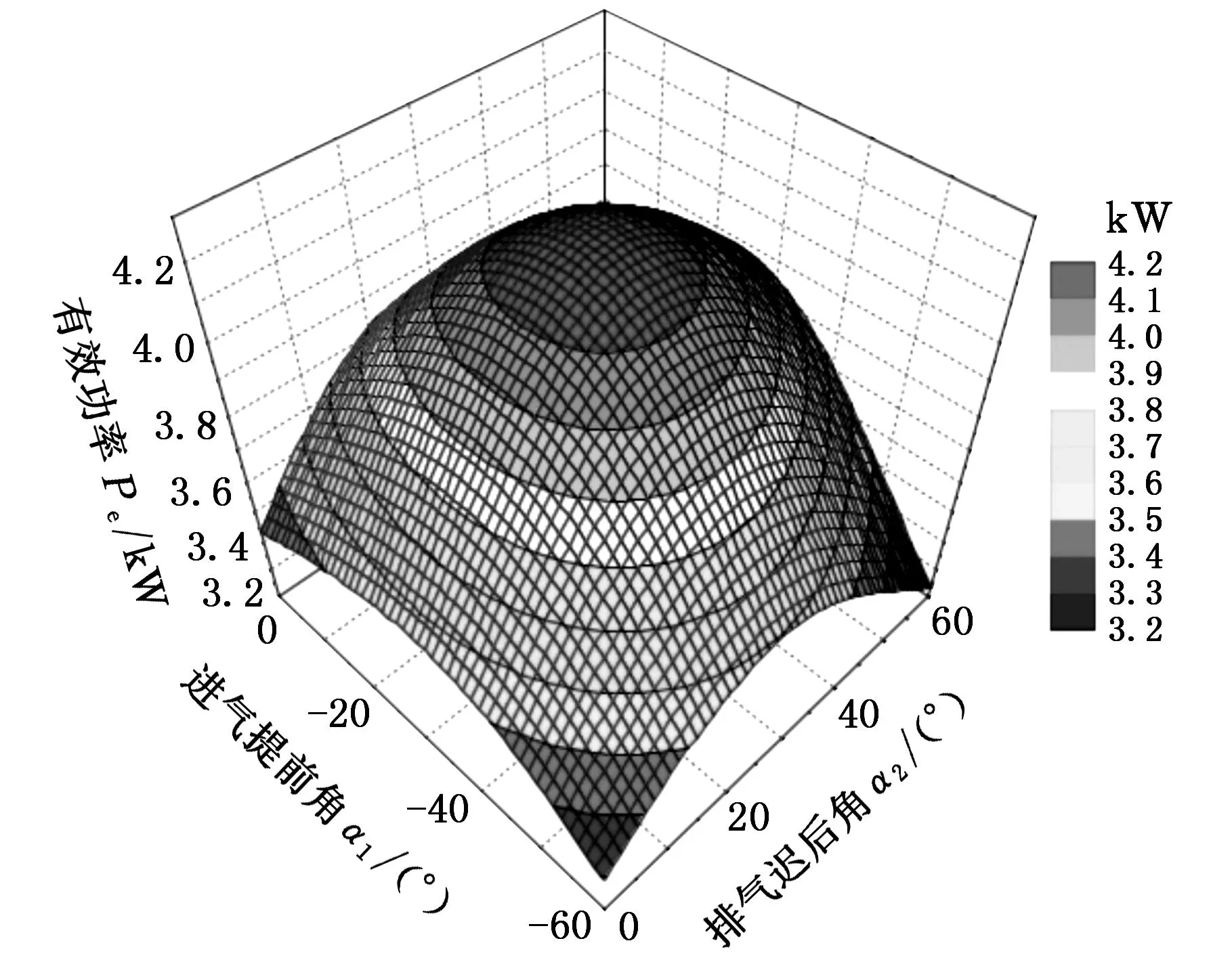
圖6　有效功率響應曲面的3D曲面

圖7　有效燃油消耗率響應曲面的3D曲面

本文有3個設計變量，2個優化目標，可以建立6個能夠直觀描繪響應曲面的3D曲面。選取其中兩個具有代表性的3D曲面，如圖6、圖7所示。從圖中可以看出，在設計變量空間中存在最優解。

3.4檢驗響應曲面的有效性

擬合精度過低的響應曲面可能會計算出錯誤的優化方案。為了確定建立的響應曲面是否能準確表示GT-Power仿真模型的特性，從而代替仿真模型進一步完成優化，十分有必要檢驗由徑向基函數法差值擬合的響應曲面的有效性。檢驗響應曲面有效性最通用的方法是在設計變量空間內隨機生成幾個測試點，并調用仿真模型進行仿真計算，然后檢查在測試點處響應曲面上對應值與仿真值的偏離程度。隨機選取的8個隨機數據點如表3所示。

表3　隨機生成的8個測試數據點

通過計算相關指數R2值描述響應曲面對仿真模型擬合程度，其計算公式為

(3)

表4　徑向基函數擬合響應曲面的R2值

3.5在響應曲面上搜尋最優值

利用驗證過的徑向基函數法建立的響應曲面，結合優化算法只需要極少的計算時間就可以完成對氣門正時的優化。優化參數設置如表2所示。優化算法采用多目標遺傳算法(MOGAⅡ)[19]，這是一種采用改進的多元搜尋精英策略的多目標遺傳算法，可以避免陷入局部最優而導致早熟收斂。遺傳算法初始種群為均勻拉丁超立方法生成的27個設計點，種群代數為100，共對2700個數據點進行了尋優，得到兩個優化目標的Pareto前沿如圖8所示，該圖表示優化算法在響應曲面上搜尋到的所有滿足條件的最優解。因為沒有設置兩個優化目標的權重，所以各個最優解是平等的。將Pareto前沿上的最優解集分析整理后，選取了5個最優解，如表5所示。

圖8　優化目標的Pareto前沿

序號進氣提前角(°)排氣遲后角(°)點火提前角(°)有效功率(kW)有效燃油消耗率(g/(kW·h))1-2831-174.24262.112-2830-174.23258.333-3029-164.23261.934-2928-174.23261.745-3127-164.22261.67

將選取的5個最優解回代到GT-Power進行仿真驗證計算，5個最優解全部滿足約束條件，由此推斷，建立的響應曲面已完全滿足優化所需的精度要求，在響應曲面上進行優化得到的最優解是準確可靠的。整個基于仿真的響應曲面氣門優化過程，一共調用了27+5+5=37次仿真，其中響應曲面的驗證調用了10次仿真，而真正建立響應曲面的過程僅用了27次，即用于試驗設計得到初始設計點。如果采用相同的DoE方法和優化算法，但直接進行優化，將對2700個設計點實施仿真，會使得計算量過大。所以響應曲面法在同樣完成優化任務的前提下，適當舍棄了過高的精度，從而大幅度提升了優化效率。

4　結論

(1)在不改變原汽油機進排氣持續期的情況下，改型的煤油機在常用轉速下，相對于原汽油機進氣提前角需要推遲10～13°，排氣遲后角需要推遲6～10°，同時為了與換氣過程相匹配點火提前角要推遲至-17～ -16°，優化后有效功率約提升4%，有效燃油消耗率基本保持不變。

(2)相比于直接優化方法，將發動機仿真模型與響應曲面法結合的方法，在保證必要計算精度的前提下，顯著節省仿真計算次數，提高優化設計效率，可以得到準確可靠的優化結果。

[1]楊致明, 李隆強. 汽油機改燒煤油或柴油的研究[C]//中國內燃機學會特種發動機分會四屆一次學術交流會論文集.北京，2006：42-50.

[2]潘鐘鍵, 何清華, 楊晶. 活塞航空重油發動機發展現狀[J]. 科技導報,2013,31(34):65-68.

Pan Zhongjian,He Qinghua,Yang Jing.Development Status of Piston Aviation Heavy Oil Engine[J].Science & Technology Review,2013,31(34):65-68.

[3]張全逾, 黎蘇, 左明偉. 配氣相位對天然氣發動機性能的影響[J].河北工業大學學報，2013,42(5):50-54.

Zhang Quanyu, Li Su, Zuo Mingwei. Study on Effect of Valve Timing on Performance of CNG Engine[J]. Journal of Hebei University of Technology, 2013,42(5): 50-54.

[4]高進, 肖龍, 任建敏, 等. 141F小型汽油機數值模擬及性能優化[J]. 內燃機,2013(4):30-33.

Gao Jin, Xiao Long, Ren Jianmin, et al. Numerical Simulation and Optimizing of 141F Gasoline Engine[J]. Internal Combustion Engines, 2013(4): 30-33.

[5]肖民, 焦濤. 6L21/31型中速柴油機配氣相位及凸輪型線優化[J]. 內燃機與動力裝置,2013,30(6):26-31.

Xiao Min, Jiao Tao. Optimization of Valve Timing and Cam Profile of 6L21 /31 Medium Speed Diesel Engine[J]. Internal Combustion Engine & Powerplant, 2013,30(6): 26-31.

[6]李露露, 黃錦成, 梁燕成, 等. 廢氣渦輪增壓汽油機可變配氣相位的優化研究[J]. 裝備制造技術,2012,28(1):8-10.

Li Lulu, Huang Jincheng, Liang Yancheng, et al. Optimize Study on Variable Valve Timing in Exhaust Turbocharged Gasoline Engine[J]. Equipment Manufacturing Technology, 2012,28(1): 8-10.

[7]黃粉蓮, 紀威, 張祿, 等. 基于OPTIMUS的柴油機配氣正時及噴油提前角的優化[J]. 農業工程學報,2012,28(15):27-32.

Huang Fenlian, Ji Wei, Zhang Lu, et al. Optimization of Valve Timing and Injection Advance Angle of Diesel Engine Based on OPTIMUS[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012,28(15): 27-32.

[8]張學文, 申立中, 雷基林, 等. 四氣門兩缸增壓柴油機配氣相位優化[J]. 昆明理工大學學報(自然科學版),2012,37(1):47-52.

Zhang Xuewen, Shen Lizhong, Lei Jilin, et al. The Valve Timing Optimization of Turbocharged & 4-Valve 2-Cylinder Diesel Engine[J]. Journal of Kunming University of Science and Technology(Natural Science Edition), 2012,37(1): 47-52.

[9]周刊, 杜愛民. 基于GT-POWER DoE的發動機多參數優化[J]. 佳木斯大學學報(自然科學版),2012,30(5):701-705.

Zhou Kan, Du Aimin. Multi-parameter Optimization of Engine Based on GT-POWER DoE[J]. Journal of Jiamusi University(Natural Science Edition), 2012,30(5): 701-705.

[10]葉年業, 劉潔, 倪計民, 等. 車用汽油機流動過程模擬及基于DoE的配氣相位優化[J]. 內燃機工程,2011,32(4):72-75.Ye Nianye, Liu Jie, Ni Jimin, et al. Flow Process Modelling of Gasoline Engine and Optimization of Valve Timing Based on DoE[J]. Chinese Internal Combustion Engine Engineering, 2011,32(4): 72-75.[11]Myers R H, Montgomery D C, Ma C C. Response Surface Methodology: Process and Product Optimization Using Designed Experiments[M]. Germany: John Wiley & Sons, 2009.

[12]Shi Yu GH-W, Reitz Rolf Deneys. Computational Optimization of Internal Combustion Engines[M]. London: Springer, 2011.

[13]Santner T J, Williams B J, Notz W I. The Design and Analysis of Computer Experiments[M].New York: Springer, 2003.

[14]Rasmussen C E. Gaussian Processes for Machine Learning[J].International Journal of Neural Systems, 2006,14(6):3011-3015.

[15]Wendland H. Scattered Data Approximation[J]. Cambridge Monographs on Applied & Computational Mathematics, 2010,10(3):336.

[16]Berbecea A. Multi-level Approaches for Optimal System Design in Railway Applications[D]. Wikipedia,France: Université Lille Nord, 2012.

[17]Persson J. Design and Optimization under Uncertainties: A Simulation and Surrogate Model Based Approach[D]. Linkoping, Sweden: Linkoping University, 2012.[18]Mckay M D, Beckman R J, Conover W J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output from a Computer Code[J]. Technometrics,2000,42(1):55-61.[19]Poles S. MOGA-Ⅱ. An improved Multi-objective Genetic Algorithm[CP/DK]. Trieste, Italy:Esteco, 2003.

(編輯郭偉)

Optimization of Valve Timing of a Kerosene Engine Based on RSM

Zhang WeiMao JianguoWei TeteHe Xiaoming

Nanjing University of Aeronautics and Astronautics,Nanjing,210016

Using optimization method of response surface based on the simulation, modified kerosene engine valve timing multi-objective optimization problem was studied. A simulation model of the engine performance was established with the intake, exhaust timing, ignition advance angle as optimization variables and with the improvement of brake power and brake special fuel consumption as the design optimization target. The results show that: relative to this gasoline engine, intake valve opening timing of modified kerosene engine must be postponed, the exhaust valve closing time must be postponed, and ignition timing must be advanced for better engine performance; and applications of response surface methodology can improve the efficiency of optimization.

kerosene engine；numerical simulation；respouse surface methodology(RSM)；valve timing

2015-06-13

國家自然科學基金青年基金資助項目(11202096)

U46DOI：10.3969/j.issn.1004-132X.2016.07.014

張偉，男，1990年生。南京航空航天大學能源與動力學院碩士研究生。主要研究方向為活塞發動機仿真與控制。毛建國，男，1957年生。南京航空航天大學能源與動力學院副教授。魏特特，男，1990年生。南京航空航天大學能源與動力學院碩士研究生。何小明，男，1972年生。南京航空航天大學能源與動力學院講師。