基于CFD的磁流體軸承潤滑膜特性分析

李　婷　馬吉恩　章　禹　方攸同

浙江大學，杭州，310027

?

基于CFD的磁流體軸承潤滑膜特性分析

李婷馬吉恩章禹方攸同

浙江大學，杭州，310027

磁流體軸承具有轉速高、密封性好、承載力強等優點，符合高速鐵路中的應用需求。提出一種磁流體軸承結構，并運用CFD方法對軸承潤滑區的承載性能以及熱效應問題進行了仿真計算，在此基礎上進一步分析了偏心率對軸承承載力及溫升的影響規律，為之后磁流體軸承的進一步設計提供幫助。

磁流體軸承；CFD；氣穴模型；潤滑特性

0　引言

高速是我國鐵路發展的主要方向。為了適應高速牽引電機軸承的高速、重載等使用要求，軸承必須具有優異的密封、振動、溫升、承載力等性能指標，才能使工作壽命延長[1]。

磁流體是由納米級尺寸的磁性固體顆粒經由界面活性劑均勻地分散在液體介質中而形成的一種磁性膠體溶液[2]。這種新型的功能性液體在具備流體特性的同時，也擁有和磁性材料相類似的特性。在外加磁場作用下，其流變性與空間形態能夠被控制。磁流體軸承就是利用磁流體的這些特殊性能而發展起來的一種新型軸承。

早在20世紀60年代，已有學者開展磁流體潤滑滑動軸承的理論研究。文獻[3]開創性地對非均勻磁場作用下的磁流體潤滑軸承進行了研究，得到了外加磁場在轉動軸上作用的磁懸浮力會使軸承的承載能力提高的結論。文獻[4]對磁流體在短軸承中的應用進行了理論研究，研究表明，在一定磁場強度范圍內，磁流體的應用令潤滑膜的承載能力大大增加，同時軸承的穩定性和剛度也得以提高。文獻[5]對耦合應力作用下的磁流體軸承承載能力進行了計算，計算結果顯示，端泄會在極大程度上降低潤滑膜承載力，高轉速則利于全油膜潤滑的建立。文獻[6]對磁流體軸承的設計以及應用進行了系統概括，并展示了近年來磁流體設計方面的成果。種種研究表明磁流體軸承相對于傳統軸承有著更多的優點。

磁流體軸承以磁流體為潤滑介質，在外加磁場的影響下，依靠磁流體的自密封能力，可以防止泄漏以及外界污染物進入軸承間隙，故具有良好的密封性；由于磁流體潤滑能夠提供平穩的低摩擦潤滑，且具有良好的可控性，因而振動小；采用磁流體潤滑的摩擦因數小，所以發熱少；由于存在磁場，使得在高速高溫情況下擁有更高的承載力。鑒于以上優點，磁流體軸承非常適合用作高速鐵路機車牽引電機軸承。

本文建立了磁流體軸承的三維仿真模型，運用Fluent軟件對磁流體軸承潤滑區特性進行仿真計算，著重分析潤滑區的承載性能以及熱效應問題。為了討論軸承承載力以及溫升情況與軸頸偏心變化的關系，分別建立了不同偏心率情況下的磁流體軸承模型，單獨改變軸頸偏心量，通過仿真分析其對軸承承載力及溫升的影響。

1　磁流體軸承的應用優勢和原理

1.1對比普通軸承的應用優勢

牽引電機軸承是保證鐵路機車安全運行的重要部件之一。對于高速鐵路機車牽引電機來說，其轉速較高、啟動快、運行久，因而對軸承的穩定性有更高的要求[7]。

目前，滾珠軸承應用最為廣泛，其在精密程度方面具有一定的優勢，但在高速以及高溫等特殊工況下工作會產生許多問題。例如，高速情況下會使潤滑脂飛濺，磨損加劇，產生振動與噪聲；高溫情況下潤滑油脂破壞會致使軸承壽命縮減等。相比較而言，空氣軸承依靠空氣不磨損接觸件的特性，使得軸承壽命大大延長。但是，空氣軸承的剛性不如機械軸承，且對生產制造工藝有很高的要求，并需要無水、無油、無塵的空氣。相比于滾珠與空氣軸承，普通油膜潤滑滑動軸承依靠其較大的黏度而具有更好的抗振能力及承載能力。但是，普通油膜潤滑滑動軸承為了實現潤滑和散熱，需要配置大功率的供油系統來不斷注入潤滑油，這使系統成本增加的同時也帶來了維護和保養的不便。

磁流體軸承是20世紀60年代配合核動力技術而發展起來的新型軸承，是以加入了磁性固體顆粒的載液(即磁流體)作為潤滑介質進行潤滑的軸承。與傳統軸承相比，這種軸承具有一系列特性：①在外加磁場的影響下，依靠磁性固體顆粒表面特殊液態膜的保護而具有更穩定的潤滑狀態，從而防止端泄以及外界污染物進入軸承間隙，起到自潤滑密封的作用；②由于加入到摩擦副中的磁性固體顆粒大小只有5～10 nm，遠小于表面粗糙度而一般不會引起磨損，故磁流體潤滑能夠提供平穩的低摩擦潤滑，振動小；③磁流體潤滑具有較小的摩擦因數，因而發熱少；④能工作于高速高溫情況，且由于磁場的存在，軸承承載能力強于同等軸承；⑤在強磁場、低偏心情況下，甚至能做到零泄漏，減少潤滑液端泄的同時簡化了系統[8-10]。

1.2磁流體軸承的原理

磁流體軸承正常工作所需要的外加磁場一般采用永磁體或直流勵磁來激發。前者可以產生磁力線形狀規則的穩定磁場，而后者則可以通過改變勵磁電流來改變磁場強度，從而進一步改進磁流體的分布。兩種磁場激發方式各有優劣。本文主要研究直流勵磁磁流體軸承，其結構如圖1所示。

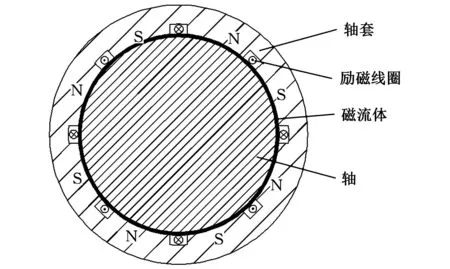
圖1　直流勵磁磁流體軸承結構

2　模型處理

本文根據高速鐵路機車牽引電機的結構，建立了轉軸以3000 r/min運行的，考慮偏心的磁流體軸承的三維模型。考慮到軸承周圍環境對軸承熱效應和熱分布的影響，加入了整段安裝軸的模型。填充軸承間隙的磁流體材料選用納米四氧化三鐵(Fe3O4)。磁流體潤滑膜的厚度為0.05 mm。所建立的三維模型如圖2所示。

圖2　三維模型

在三維建摸的基礎上，完成了對整個模型的網格劃分。網格劃分主要考慮以下兩方面的影響：一方面，要保證網格的密度，特別是關鍵區域的網格，以確保計算的精度；另一方面，對于外部環境區域里對關鍵特性分析影響不大的部分需進行網格數目的降低，以提高仿真計算的速度。根據以上兩條原則，對磁流體潤滑膜處的剖分采用等分形式并進行加密。軸套及安裝軸承的該段軸采用漸進網格的形式。其中，對于軸套的剖分，采用沿徑向由外到內網格逐漸變細，而對于安裝軸承的該段軸則采用沿徑向由外到內網格逐漸變粗。網格剖分結果如圖3所示。

圖3　網格剖分結果

3　邊界條件的施加

3.1熱邊界條件

工程中傳熱現象從物理本質上區分時，通常有三種基本形式，即熱傳導、對流換熱及輻射換熱。熱傳導是指熱量由高溫物體傳向低溫物體或者由同一物體的高溫部分傳向低溫部分的能量交換過程，可以在固體、液體以及氣體中發生，是固體傳熱最主要的方式；對流換熱是指在用流體的宏觀流動將所含熱能從物體中一處遷移到另一處的過程中，流動的流體與其所經固體表面之間所發生的熱交換過程，一般可分為自然對流和強迫對流兩種方式；輻射換熱則是指高溫物體以電磁波形式傳遞熱量的過程[11]。本文所研究的電機采用強制對流的冷卻方式，輻射換熱可以忽略不計;由于磁流體潤滑屬于流體動壓潤滑狀態，以對流散熱為主要方式，傳導散熱通常可以不予考慮。

在本文計算中，將軸承安裝位置的該段軸設置為對流換熱邊界條件，由于軸的溫度變化相對并不明顯，故將其他與軸承相距較遠的幾段軸設置為恒溫邊界條件，將軸的外表面和磁流體潤滑膜的內表面，軸套的內表面和磁流體潤滑膜的外表面設置為流固耦合面，并將前者設置為旋轉壁面，轉速與軸頸轉速相同，為3000 r/min，后者設定為固定壁面邊界條件。

開啟能量方程，由于是黏性流動，故在能量方程中考慮黏性生成熱(viscous heating)。

3.2空化邊界條件

滑動軸承內的空穴現象，主要是因為溶解在潤滑液內的空氣由于外界壓力變低，其體積膨脹析出而造成[12-13]。當考慮潤滑膜的空化效應時，壓力達到一定值后潤滑膜中就可能會有氣泡出現，此時軸承間隙處的流動是一種多相流，需要考慮氣相和液相之間的相互耦合作用，因此需要引入多相流模型。本文選用Mixture多相流模型以及Zwart-Gerber-Belamri空化模型。

4　不考慮空化的潤滑膜壓力和溫升分析

在上述網格劃分以及邊界條件設置的基礎上，不開啟空化模型，從主軸壁面開始初始化，使用Fluent進行迭代求解直至收斂，可得到磁流體潤滑膜的壓力以及溫度云圖，以偏心率ε=0.5時的工況為例的壓力和溫度云圖如圖4、圖5所示。圖6為軸承內理論潤滑膜壓力分布。

圖4　磁流體潤滑膜壓力云圖

圖5　磁流體潤滑膜溫度云圖

圖6　軸承內理論潤滑膜壓力分布

由圖4可知，潤滑膜壓力分布有兩個非常明顯的壓力集中區，一個呈現正壓，一個呈現負壓，在最小潤滑膜厚度區被明顯地分隔開來。由于軸的偏心和順時針轉動，在A區域產生了收斂楔形，從而產生了磁流體潤滑膜的正壓力。在收斂區，隨著間隙的減小，壓力逐漸增大達到正壓峰值后減小，通過最小油膜厚度處后進入發散區(B區域)，此時由于潤滑膜速度迅速增大，很快形成了一個真空區域，達到負壓峰值，之后逐漸恢復到正壓，趨于平穩。這與圖6所示的軸承內理論潤滑膜壓力分布規律一致。磁流體潤滑膜中間位置沿周向壓力分布曲線如圖7所示(此處起點位置與圖6不同，故角度不作對應)。正壓區域最大壓力為2 224 565 Pa，負壓區最大壓力為2 033 140 Pa，在正壓力和負壓力的共同作用下，產生承載力來支撐軸頸，并平衡外載荷。由Fluent計算水膜合力大小為2169.2 N。

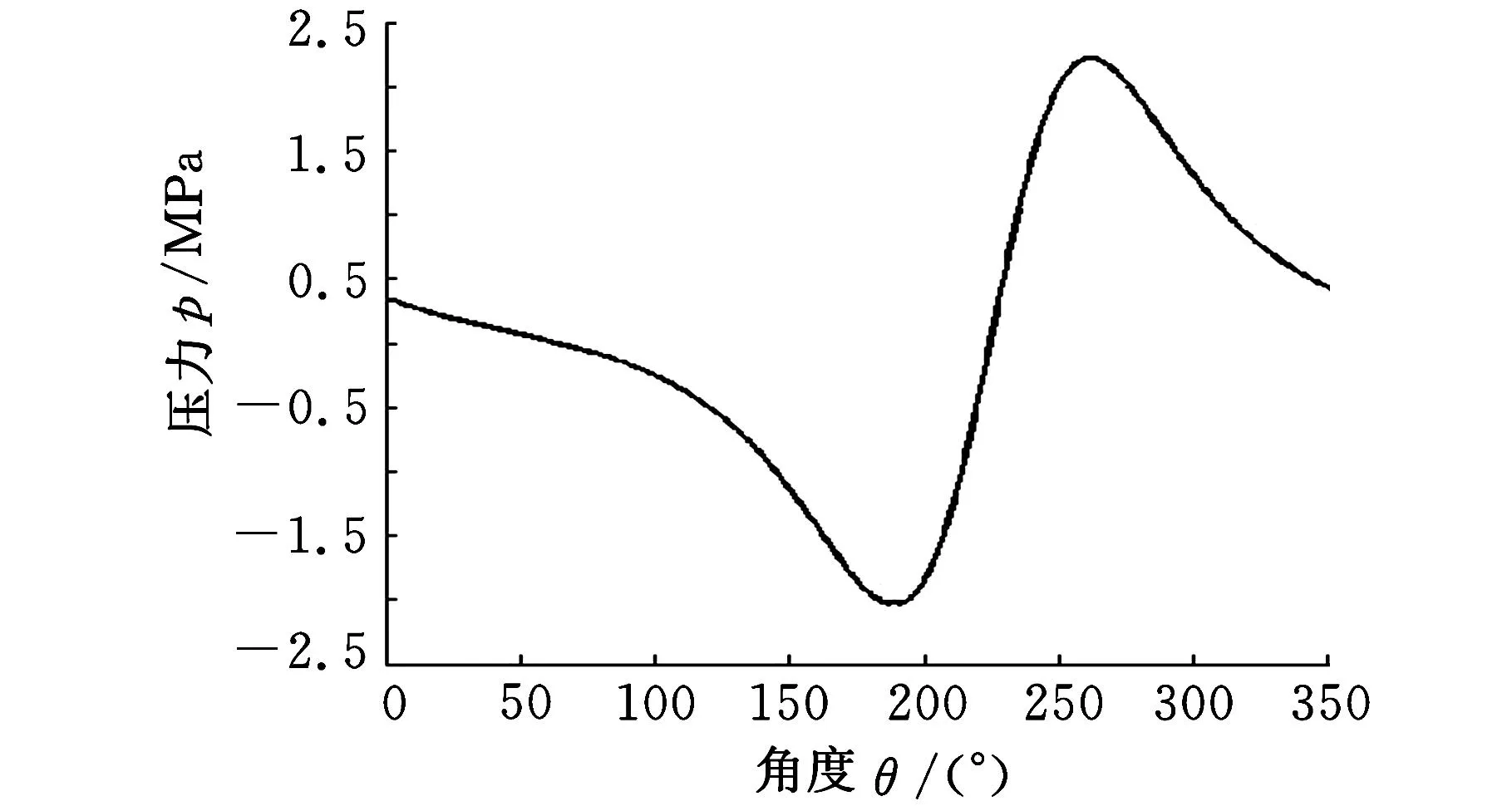
圖7　潤滑膜中心面周向壓力分布

圖5所示為轉速3000 r/min時的三維溫度場分布云圖。由圖可知，發散區(C區域)的最高溫度為98.3 ℃，離開此區域，潤滑膜溫度開始逐漸降低。可以看到，發散區的溫度普遍偏高，且同收斂區的溫差約為20 ℃。潤滑膜溫度沿軸向從中間向兩端逐漸降低，溫度分布在36～80 ℃范圍內。可知，磁流體潤滑膜處的熱量在軸向方向上，沿軸向兩端散熱情況良好。

5　加入空化模型的潤滑膜壓力和溫升分析

由于發散區負壓的存在，當壓力達到一定值，潤滑膜中就可能會有氣泡出現，引起氣穴現象。這將導致潤滑膜在負壓區迅速破裂并進一步對壓力分布產生影響。因此在計算時加入空化模型是很有必要的。

本文選用Mixture多相流模型以及Zwart-Gerber-Belamri空化模型進行了仿真計算。初始設置時將磁流體相體積分數設為100%，空氣相體積分數設為0，最終通過仿真得到最后的空氣體積分數。圖8～圖12為不同偏心率ε下的磁流體潤滑膜壓力分布云圖。

圖8　ε=0.1下的磁流體潤滑膜壓力分布云圖

圖9　ε=0.3下的磁流體潤滑膜壓力分布云圖

圖10　ε=0.5下的磁流體潤滑膜壓力分布云圖

圖11　ε=0.7下的磁流體潤滑膜壓力分布云圖

圖12　ε=0.9下的磁流體潤滑膜壓力分布云圖

對比圖4與圖8c可以看出，沒有采用空化模型時，潤滑膜在發散階段的最小壓力達-2.03 MPa，這與實際情況完全不符，而采用空化模型的計算結果更符合實際。

在仿真實驗中得知，加入空化模型后，在收斂區內，隨著間隙的減小，壓力升高，在最小間隙前某一角度，壓力達到最大值，之后壓力有所下降。當經過最小間隙進入發散區后，隨著間隙變大，由于油膜破裂，沒有產生負壓，而只有很小的正壓，并且壓力基本保持不變，其值為7550 Pa。隨著偏心率的增大，正壓區域內的壓力峰值隨之增大，高壓區范圍越來越小。這是由于潤滑膜產生楔形的直接原因是軸頸的偏心，偏心距的增大會使得磁流體潤滑膜的楔形效應增強，從而提高了磁流體潤滑膜的承載力。潤滑膜最大壓力與偏心率之間的規律曲線如圖13所示。

圖13　磁流體潤滑膜最大壓力與偏心率的關系

從偏心率0.5工況下的磁流體潤滑膜氣相體積分布的仿真可知，在收斂區內，幾乎全部潤滑面上都有完整的磁流體膜。當經過最小間隙進入到發散區后，隨著間隙的變大，在某一角度油膜開始破裂。并且油膜氣化比例隨著間隙的變大而增大。磁流體潤滑膜氣相體積分數如圖14所示。

圖14　磁流體潤滑膜氣相體積分數(ε=0.5)

圖15為加入空化模型后，偏心率0.5工況下的磁流體潤滑膜溫度分布云圖。與圖5對比可知，考慮空化后，潤滑膜的最高溫度由98.3 ℃下降到了76.6 ℃，高溫區仍然出現在發散區范圍內，但所占面積有所減小。整體來看，散熱情況較圖5更為良好。

圖15　考慮空穴效應的溫度分布云圖(ε=0.5)

6　結論

(1)對比了磁流體軸承相對于其他軸承的應用優勢，分析了其用作高速鐵路機車牽引電機軸承的理論可行性。

(2)提出了一種磁流體軸承結構，建立了其三維模型并進行了網格剖分，應用CFD方法對模型進行了仿真分析，得到了軸承潤滑膜溫度和壓力的分布規律，驗證了模型的合理性。

(3)考慮了滑動軸承內的空穴效應，為了找到磁流體潤滑膜承載性能和軸頸偏心之間的關系，建立了不同偏心率的潤滑膜模型，通過仿真，分析了不同偏心率下磁流體潤滑膜作用力的變化規律。

[1]何強, 李安玲, 張繼祝,等. 高速列車軸承的發展趨勢[J]. 徐州工程學院學報(自然科學版), 2012, 27(1):58-64.

He Qiang, Li Anling, Zhang Jizhu, et al. The Development Trend of High-speed Railway Bearing[J]. Journal of Xuzhou Institute of Technology(Natural Sciences Edition), 2012, 27(1):58-64.

[2]顧紅, 王先逵, 祝琳華,等. 磁流體技術及發展方向綜述[J]. 昆明理工大學學報(理工版), 2002, 27(1):55-57.

Gu Hong, Wang Xiankui, Zhu Linhua, et al.The Review of Magnetic Ferrofluid Technology Development and Its Application[J]. Journal of Kunming University of Science and Technology(Natural Science Edition), 2002, 27(1):55-57.

[3]Tarapov I E. Movement of a Magnetizable Fluid in the Lubricating Layer of a Cylindrical Bearing[J]. Magnetohydrodynamics, 1972(8):444-448.

[4]Tipei N. Theory of lubrication with Ferrofluids: Application to Short Bearings[J]. ASME, 1982,104:510-515.

[5]Das N C．A Study of Optimum Load-bearing Capacity for Slider Bearings Lubricated with Couple Stress Fluids in Magnetic Field[J]. Tribology International, 1998,31(8)：393-400.

[6]Ochonski W.Sliding Bearings Lubricated with Magnetic Fluids[J].Industrial Lubrication and Tribology,2007,59(6):252-265.

[7]施洪生, 張奕黃,高培慶. 高速牽引電機軸承關鍵技術的發展趨勢[J]. 機車電傳動, 2007(2): 1-5.

Shi Hongsheng, Zhang Yihuang, Gao Peiqing. Development Trend of Critical Technologies for Bearing of High-speed Traction Motor[J]. Electric Drive for Locomotive, 2007(2):1-5.

[8]王建梅, 孫建召, 薛濤,等. 磁流體潤滑技術的發展[J]. 機床與液壓, 2011, 39(6):109-112.

Wang Jianmei, Sun Jianzhao, Xue Tao, et al. The Development of Magnetic Fluid Lubricating Technology[J]. Machine Tool & Hydraulics, 2011, 39(6):109-112.

[9]王瑞金, 王常斌. 磁流體技術的工業應用[J]. 力學與實踐, 2004, 26(6):8-13.

Wang Ruijin, Wang Changbin.The Industrial Apllications of the Magnetic Fluid Technique[J]. Mechanics and Engineering, 2004, 26(6):8-13.

[10]何世權,楊逢瑜,楊瑞. 滑動軸承磁流體薄膜和潤滑特性的研究[J]. 潤滑與密封, 2007,32(1):126-128.

He Shiquan,Yang Fengyu,Yang Rui. Research on Lubricating Characteristic of Thin Film and Glide Bearings Affected by Magnetic Fluid[J]. Lubrication Engineering, 2007,32(1):126-128.

[11]魏永田, 孟大偉, 溫嘉斌. 電機內熱交換[M]. 北京：機械工業出版社, 1998.

[12]Guo Zenglin, Hirano T, Kiyk R G. Application of CFD Analysis for Rotating Machinery—Part I: Hydrodynamic, Hydrostatic Bearings and Squeeze Film Damper[J]. J. of Engineering for Gas Turbines and Power APRIL, 2005,127:445-451.

[13]張楚, 楊建剛, 郭瑞,等. 基于兩相流理論的滑動軸承流場計算分析[J].中國電機工程學報,2010,30(29):80-84.

Zhang Chu, Yang Jiangang, Guo Rui, et al. Simulation of Journal Bearing Flow Field Using Computational Fluid Dynamics Two Phase Flow Theory[J]. Proceedings of the CSEE, 2010,30(29):80-84.

(編輯郭偉)

Lubrication Characteristics Analyses of Ferrofluid Bearing Based on CFD Simulation

Li TingMa JienZhang YuFang Youtong

Zhejiang University,Hangzhou,310027

Ferrofluid bearing had a series of advantages, like high speed, good sealing, strong bearing capacity, etc.,which complied the needs of high-speed railway. A three-dimensional model of ferrofluid bearing was built and the simulation about the bearing and thermodynamic characteristics were carried out based on CFD. And then, further analyses of the influences of eccentricity were made, which laid the foundation for subsequent design of ferrofluid bearing.

ferrofluid bearing; computational fluid dynamics(CFD); cavitation model; lubrication performance

2015-03-29

國家自然科學基金資助項目(51105331, 51177144)；國家高技術研究發展計劃(863計劃)資助項目(2011AA11A101)

TH133.3;TH117.2DOI：10.3969/j.issn.1004-132X.2016.07.015

李婷，女，1990年生。浙江大學電氣工程學院碩士研究生。主要研究方向為磁流體軸承。馬吉恩，女，1979年生。浙江大學電氣工程學院助理研究員。章禹，男，1993年生。浙江大學電氣工程學院本科生。方攸同，男，1962年生。浙江大學電氣工程學院教授。