一題多解與一題多究

山東省聊城大學數學科學學院　(252000)

姜曉潔*　于興江

?

一題多解與一題多究

山東省聊城大學數學科學學院(252000)

姜曉潔*于興江

一題多解與一題多究可以深入了解題目的設計意圖、設計方法，牢固掌握題目相關知識，是中學教師提升自身知識素質的最佳途徑.筆者就2015年高考理科數學四川卷第20題為例，進行了多解分析和推廣探究,并將本題推廣到雙曲線和拋物線上，得到了相似的結論.

1　原題呈現

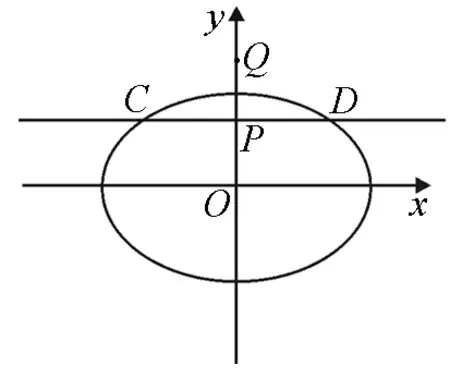
圖1

(Ⅰ)求橢圓E的方程;

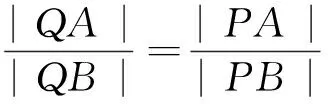
2　解法探究

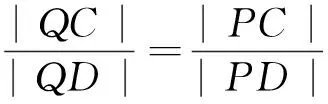
|QD|.因此Q點在y軸上，設Q(0,y0).

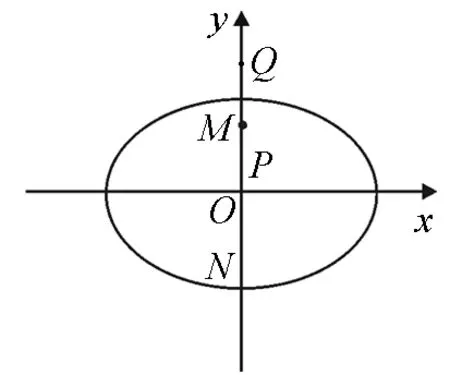
圖2

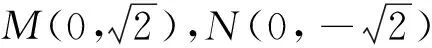
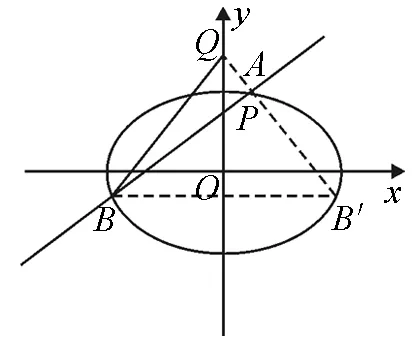
圖3

以下證明，對任意的直線l，Q(0,2)均滿足條件.

如圖3，當直線l斜率不存在時，顯然成立，以上已證.

當直線l斜率存在時，設直線l方程為y=kx+1，A(x1,y1),B(x2,y2).

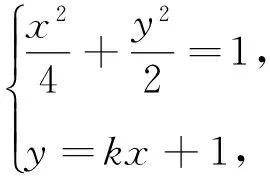
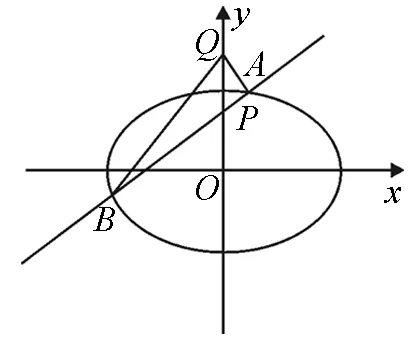
圖4

解法2:由解法1可知，若存在不同于點P的定點Q，則只能是Q(0,2).以下證明，對任意的直線l，Q(0,2)均滿足條件.

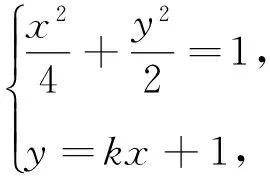
3　推廣探究

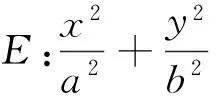
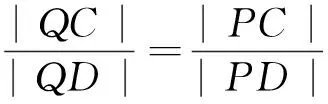
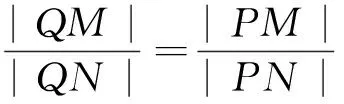
以下證明，對任意的直線l，Q(0,b2)均滿足條件.

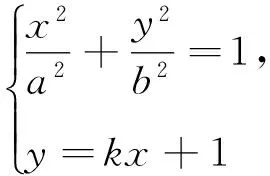
(a2k2+b2)x2+2a2kx+a2-a2b2=0.

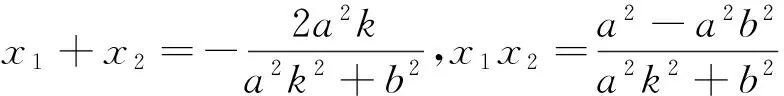
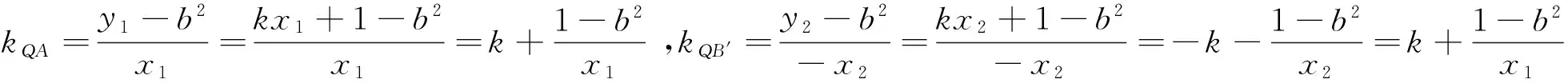
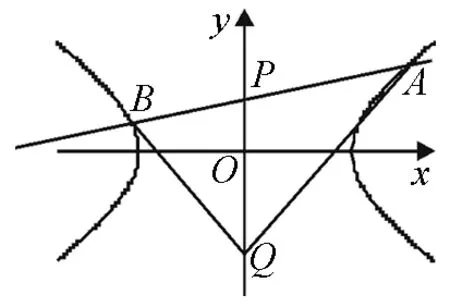
圖5

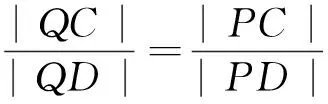
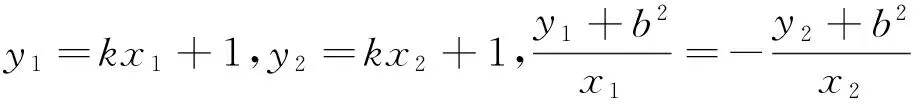
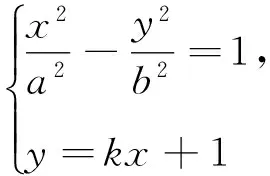
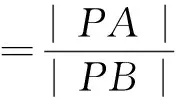
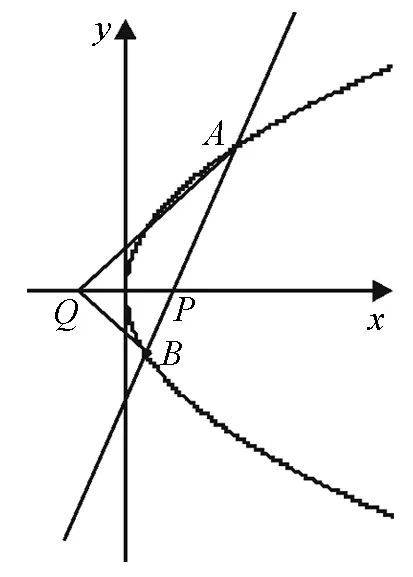
圖6

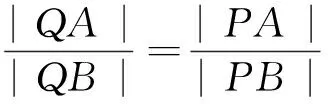
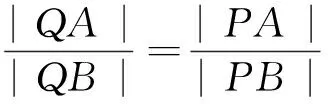
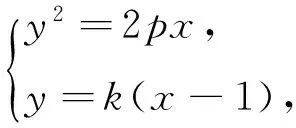
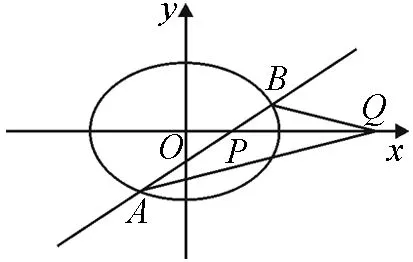
圖7

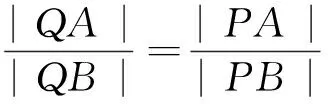
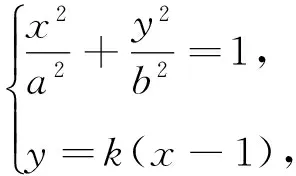
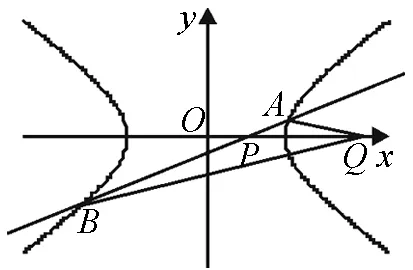
圖8

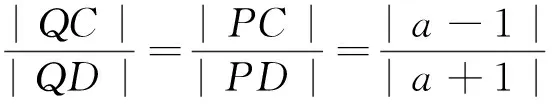
以下證明，對任意的直線l，Q(a2,0)均滿足條件.

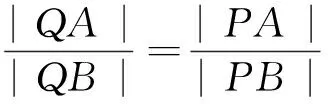
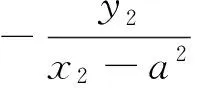
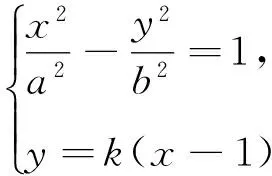
[1]柳俊婷，于興江，“圓錐曲線的一個性質”再探究[J].中學數學研究(江西)，2015，11.

[2]李靜，于興江.一道高考題的多解及推廣[J].中學數學研究(江西)，2013，12.

[3]孫玉英，于興江.探究 引申 剖析 啟示— 一道高考題的賞析[J].中學數學研究(江西)，2013，10.

[4]柳俊婷，于興江， 2015年山東理科第20題的多解分析及探究[J].中學數學研究(江西)，2015，8.

* 作者現為2015級碩士研究生.