一種重型燃氣輪機建模及其參數估計的方法

黃玉柱，　蔣洪德

(清華大學 燃氣輪機與煤氣化聯合循環國家工程研究中心，北京 100084)

?

一種重型燃氣輪機建模及其參數估計的方法

黃玉柱，蔣洪德

(清華大學 燃氣輪機與煤氣化聯合循環國家工程研究中心，北京 100084)

為研究燃氣輪機系統動態特性，基于Rowen模型建立了燃氣輪機及其控制系統的數學模型，利用燃氣輪機現場運行數據，運用質量守恒、能量守恒和動量守恒原理以及熱力學和傳熱學等基本公式，推算和估計模型的相關參數.以GE MS6001FA型燃氣輪機為研究對象，給出燃氣輪機建模及參數估計的具體方法和過程。結果表明：該模型能夠正確反映燃氣輪機的動態特性，符合機組運行規律，具有很好的研究和參考價值.

燃氣輪機； Rowen模型； 參數估計； 現場運行數據

近年來，我國電力工業迅猛發展，電網峰谷差日趨增大以及能源結構調整使得燃氣輪機及其聯合循環發電快速發展[1].借助計算機技術，建立燃氣輪機系統模型并進行數字仿真逐漸成為研究其動態特性最有效的手段[2-5].在燃氣輪機建模中，最常用的模型為Rowen模型[6-8]，作為一類重要的簡化模型，其從控制角度提出了一種新的燃氣輪機建模思路，擺脫了傳統的用微分方程組表示燃氣輪機動態特性的方法，同時借鑒了模塊化建模思想，以方塊圖表示系統數學模型，將各環節用不同方塊單元來表示，然后串聯起來形成燃氣輪機整體模型，使得模型的擴充、簡化和維護都很方便，具有較好的模型精度[9-10].然而，Rowen模型并未給出模型參數的具體含義和參數估計的方法[7-8].

筆者給出燃氣輪機模型參數的具體含義，并利用現場運行數據，運用質量守恒、能量守恒和動量守恒原理以及熱力學和傳熱學等基本公式推算和估計模型相關參數.同時以GE MS6001FA型燃氣輪機為研究對象，基于現場運行數據，給出燃氣輪機建模和參數估計的具體方法及過程.

1　燃氣輪機系統分析

燃氣輪機主體結構主要由壓氣機、燃燒室、透平和轉軸組成.燃氣輪機正常工作時，工質依次經過吸氣壓縮、燃燒加熱、膨脹做功和排氣放熱4個階段，完成由熱變功的熱力循環.具體過程如下：由壓氣機將空氣壓縮到一定壓力，送到燃燒室與燃料摻混燃燒，產生高溫高壓的燃氣，高溫高壓燃氣從燃燒室流入透平，并在透平中膨脹做功，最后燃氣壓力下降，排至大氣中.透平產生的功一部分用于驅動壓氣機，其余部分用以帶動負載，如推動與燃氣輪機同軸的發電機發電.在結構上，燃氣輪機主要分為重型燃氣輪機和航改型燃氣輪機，筆者主要討論單軸重型燃氣輪機，其結構如圖1所示.

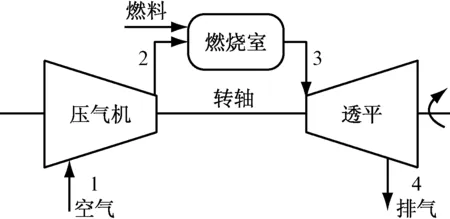
1-壓氣機入口；2-壓氣機出口；3-燃燒室出口(透平入口)；4-透平出口.

圖1單軸重型燃氣輪機結構示意圖

Fig.1Schematic structure of a typical single-shaft gas turbine

燃氣輪機簡單循環熱力過程如圖2所示，其中1～2s表示壓氣機的等熵壓縮過程，2s～3表示燃燒室內的等壓燃燒過程，3～4s表示透平的等熵膨脹過程，4s～1表示排入大氣后的等壓冷卻過程.而實際燃氣輪機循環中壓縮過程(1～2)和膨脹過程(3～4)都不是等熵的，使得實際壓縮功大于等熵壓縮功，實際膨脹功小于等熵膨脹功，即壓氣機等熵效率ηc和透平等熵效率ηt均小于1.在實際燃燒過程中，由于存在不完全燃燒和散熱損失，燃燒室燃燒效率ηb小于1.通常，散熱損失很小，可忽略，即ηb取決于不完全燃燒的程度.

圖2　燃氣輪機簡單循環溫-熵圖

2　燃氣輪機建模及參數估計

基于Rowen模型，建立簡單循環燃氣輪機及其控制系統數學模型，如圖3所示.考慮到在簡單循環下，入口可轉導葉(IGV)只在機組啟停過程中進行調整，而在正常運行下，IGV將保持最大開度；只有在燃氣-蒸汽聯合循環時需要調整IGV開度來調節壓氣機流量，以保持燃氣輪機出口溫度不變，進而保證部分負荷下聯合循環仍能獲得較高效率.故在簡單循環下，暫不考慮IGV的控制.

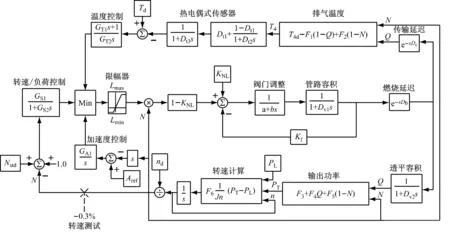
圖3　燃氣輪機及其控制系統的數學模型

2.1燃氣輪機建模及參數估計

燃氣輪機模型主要包括溫度模塊、燃燒模塊、功率模塊和轉子模塊.下文將詳細給出各模塊建模及參數估計的方法.

根據圖2，壓氣機等熵效率ηc和透平等熵效率ηt分別為

(1)

(2)

式中：hi、Ti分別為圖2中燃氣輪機簡單循環在i(i=1,2,2s,3,4,4s)處空氣(或燃氣)的焓值和溫度，kJ/kg和K.

圖2中1～2s和3～4s的等熵(可逆絕熱)過程初、終態參數的關系可由理想狀態方程及絕熱過程方程求得.

(3)

(4)

式中：p1、p2、p3和p4分別為壓氣機入口、壓氣機出口、透平入口和透平出口的壓力，kPa；πc、πt分別為壓氣機的壓縮比和透平的膨脹比；rc、rh分別為低溫段(壓氣機)和高溫段(燃燒室和透平)的比熱容比.

在燃燒室內壓力損失一般變化不大，可認為總壓恢復系數ζb為常數，即p3=ζbp2，于是πt=ζbπc.基于文獻[7]～文獻[10]，低溫段(壓氣機)和高溫段(燃燒室和透平)空氣和燃氣的比熱容和比熱容比分別為：cpc=1.005 kJ/(kg·K)，cph=1.157 kJ/(kg·K)，rc=1.4，rh=1.33.進一步可得壓氣機和透平出口溫度T2和T4分別為

(5)

(6)

在燃燒室內，來自壓氣機的壓縮空氣與經燃料噴嘴噴入的燃料混合、燃燒，將儲藏在燃料中的化學能轉化為熱能，形成高溫高壓燃氣，進入透平中膨脹做功.按照燃料發熱量的定義(燃燒室出口燃氣溫度降至與入口空氣溫度相同時所放出的熱量等于燃料的發熱量)，得到燃燒室的熱平衡方程：

(7)

式中：qm,2、qm,f分別為壓氣機出口空氣的質量流量(以下簡稱壓氣機出口質量流量)和加入燃燒室的燃料質量流量(以下簡稱燃料量)，kg/s；T3為燃燒室出口溫度，K；QLHV為燃料靜比能(即低位發熱量)，kJ/kg.

考慮到壓氣機出口的空氣質量流量遠大于進入燃燒室的燃料量，近似認為燃燒室出口質量流量qm,3=qm,2+qm,f≈qm,2.一般燃燒效率ηb的取值范圍為0.96～0.99，假定ηb=0.99，利用式(7)可得

(8)

在實際中，燃氣輪機內質量流量、壓力和溫度等參數都與其轉速密切相關，具有高度復雜的非線性關系.而在Rowen模型中，通過限定燃氣輪機轉速在額定轉速的95%～107%范圍內，近似認為燃氣輪機各參數與轉速的關系可簡化為某特定的線性關系.基于此，可推導出燃氣輪機排氣溫度(即透平出口溫度T4)和輸出功率PT的表達式.在額定轉速下，假定壓氣機出口質量流量qm,2與其ISO條件(即大氣壓力101.325 kPa，溫度 15 ℃，相對濕度60%)下的額定值qm,2d相等，即qm,2=qm,2d，聯立式(5)、式(6)和式(8)可得

(10)

式中：Q為實際燃料量qm,f與額定燃料量qm,fd之比；下標d表示ISO條件下對應的燃氣輪機額定參數，即設計值.

進一步可得不同轉速下排氣溫度T4：

(11)

式中：N為實際轉速n與額定轉速nd之比；系數F2表征排氣溫度T4與轉速偏差(1-N)的線性關系，其值約為額定排氣溫度T4d的0.55～0.65倍.

假定壓氣機出口質量流量qm,2等于透平出口質量流量qm,4，即qm,2=qm,4，則燃氣輪機輸出功率PT為

(12)

在額定轉速下，假定qm,2=qm,2d，根據式(5)、式(6)、式(8)和式(12)可得

(13)

(15)

進一步可得不同轉速下輸出功率PT：

(16)

式中：系數F5表征輸出功率PT與轉速偏差(1-N)的線性關系，其值約為額定功率PTd的0.5～0.67倍.

轉子是燃氣輪機中主要的慣性環節，用來連接壓氣機、透平和發電機，完成透平做功的傳遞.根據動量守恒原理，建立轉子動態模型:

(17)

式中：J為轉子的轉動慣量，kg·m2；PL為負載功率，kW；系數F6=91.282.

如圖3所示，建立燃燒延遲環節來反映燃料噴入與燃燒完成之間的延遲，對于當代重型燃氣輪機，燃燒延遲系數Db多為ms量級.

2.2控制和測量回路建模及參數估計

在簡單循環下，不考慮IGV控制，燃氣輪機控制系統數學模型主要包括轉速/負荷控制模型、溫度控制模型、加速度控制模型及相關測量回路模型.

為了適應不同的負載特性，轉速/負荷控制作為最基本的控制回路，主要分為“有差調節”和“無差調節”.燃氣輪機發電并網運行時采用“有差調節”，以便對負荷進行調節，轉速調節器為比例模塊.具體過程是通過調整轉速基準值，使得轉速基準與實際轉速存在偏差，從而改變輸出的燃料基準，最終達到調整負荷的目的.當燃氣輪機處于獨立電網或用于機械驅動時采用“無差調節”，無差調節器為比例積分模塊，保證實際轉速與參考轉速一致.本文所研究的燃氣輪機用來并網發電，采用“有差調節”，且對應的不等率取3%～7%，其模型見圖3.

溫度控制主要限制燃氣輪機透平入口溫度(即燃燒室出口溫度T3)，防止透平超溫.實際運行中，由于透平入口溫度T3很高，難以長期直接測量和控制，于是通過控制排氣溫度T4來限制T3.溫度調節器為比例積分模塊.因此，溫度控制回路可近似為比例積分環節，其數學模型見圖3.

在某些特殊情況下(如起動加速、甩負荷)，加速度控制能夠抑制轉子動態超速，保證機組的安全.該控制回路可通過對實際轉速微分得到轉子加速度，然后將其與參考值進行比較，再進行調節來實現.加速度調節器為積分模塊，其數學模型見圖3.

為了保證燃氣輪機各控制回路能協調一致，每個控制回路要經過最小值選擇器后輸出最小的燃料基準值(即燃料閥門給定值)，并將其輸入燃料伺服系統.控制系統模型相關參數可根據實際控制系統的參數設置得到.

在燃料系統中，通過調整燃料(液體或氣體)閥門的位置(開度)來調節進入燃燒室的燃料量.盡管液體與氣體燃料閥門調整存在差別，但都是通過閥門位置的閉環反饋控制來實現的，基本原理見圖4.燃料閥門調整的控制回路模型如圖5所示.對于液體燃料閥門的調整，通過改變旁通燃料來調節進入燃燒室的燃料量，即調整旁通調節閥；其模型參數a和b的值可參考廠商提供的數據，而Kf要保證整個閥門調整回路的增益為1，即Kf=1-a.對于氣體燃料閥門的調整，可直接調整燃料通路上閥門開度來調節進入燃燒室的燃料量；其模型參數a=1，Kf=0，b根據廠商提供數據得到.

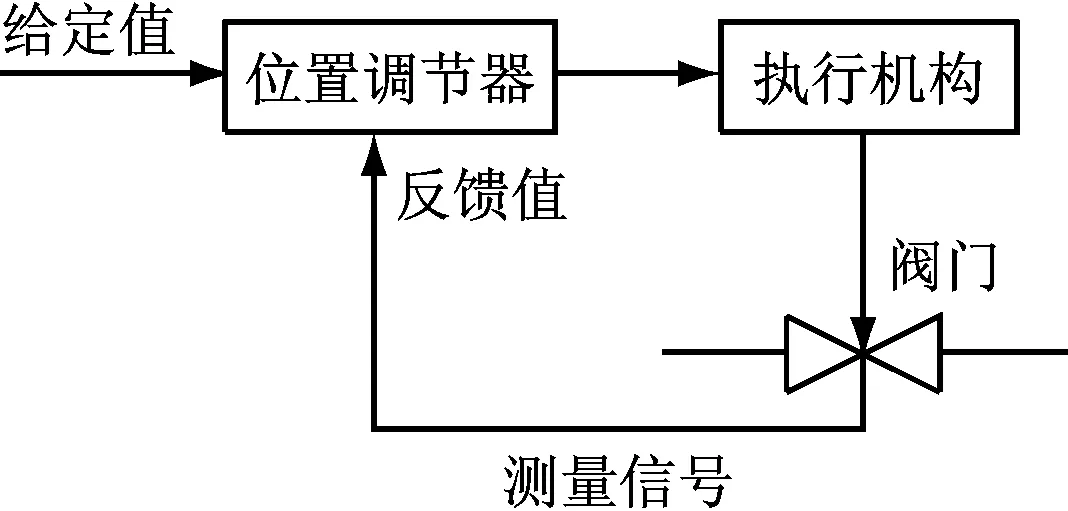
圖4　燃料閥門調整原理圖

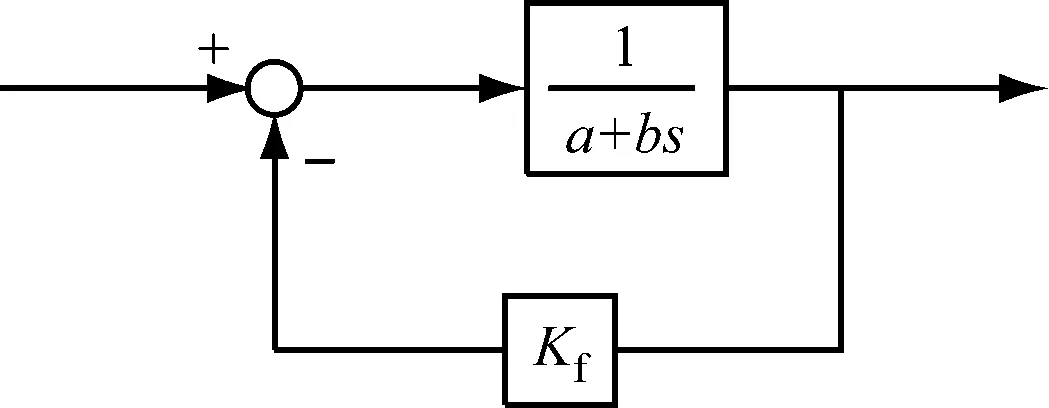
圖5　燃料閥門調整的控制回路模型

考慮到燃料相關管路系統的容積特性，當閥門動作后，進入燃燒室的燃料量的變化會存在一定延遲.同理，考慮到透平的容積特性，進入透平的燃氣量的變化也會存在延遲.在建模時，通過設置延遲時間來集中反映燃氣輪機各部件的容積特性對其質量流量的影響.假定某一部件容積如圖6所示，基于流量連續方程，可得容積延遲時間參數Dv為

(18)

(19)

式中：pv為該容積內穩態壓力，kPa；qm,v為該容積的穩態質量流量，kg/s；V為容積，m3；v為比體積，m3/kg；Φ為在溫度Tv下由壓力變化而導致的該容積內密度ρ(ρ=1/v)的變化,kg/m3.

為了計算Φ，假定pv1和pv2分別為該容積內某一較小壓力波動產生的前后壓力值，v1和v2分別對應pv1和pv2下的比體積，且此期間內Tv保持不變，于是近似可得Φ：

(20)

根據式(18)～式(20)計算得到該容積延遲時間參數Dv.對于氣體燃料和工質，由于其可壓縮性，比體積變化較大，所以相應的容積延遲時間也會較長.

圖6　燃氣輪機部件容積示意圖

通常采用熱電偶式傳感器測量得到燃氣輪機排氣溫度.首先，考慮到排氣溫度測點位置，燃燒室內燃料與空氣摻混燃燒形成的高溫燃氣傳輸到透平出口溫度傳感器處需要一定的時間，因此從燃燒放熱到傳感器測得溫度變化過程中存在時間延遲，延遲時間參數Dc取決于重型燃氣輪機的尺寸和燃氣的平均流速，一般為ms量級.熱電偶式傳感器的基本結構如圖7所示.從圖7中傳感器測量端的結構可知，熱傳遞過程的影響將導致燃氣溫度的測量有一定的延遲.基于文獻[10]，熱電偶式傳感器測量端建模如下：

(21)

式中：Tmea和Texh分別為燃氣輪機排氣溫度的測量值和實際值；Dt1、Dt2為該模型相關參數，可由相應的熱電偶式傳感器結構參數確定.

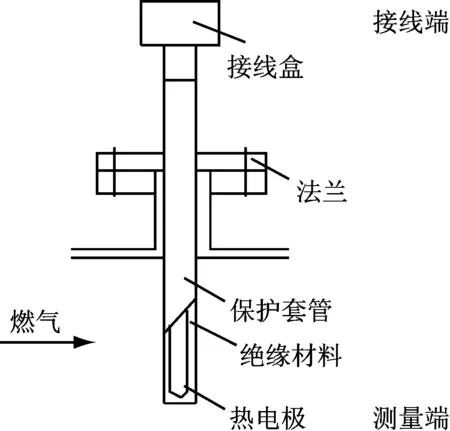
圖7　熱電偶式傳感器結構示意圖

考慮到傳感器測量處理過程本身具有的延遲特性，存在熱電偶式傳感器延遲參數Dt3，可通過實際傳感器的響應時間確定.

3　GE MS6001FA型燃氣輪機建模

信息采集、存儲和處理技術的普遍利用和不斷發展，使得燃氣輪機運行過程中大量生產以及設備和過程數據的收集和存儲成為可能，這是燃氣輪機建模及參數估計的基礎.GE MS6001FA型燃氣輪機額定工況(ISO條件)下的性能參數如表1所示.該機組的燃料為天然氣，燃氣輪機控制系統數學模型如圖3所示，其中未考慮IGV的建模.

表2給出了GE MS6001FA型燃氣輪機一組典型的現場運行數據.在建模中，機組轉速限定為額定轉速的95%～107%，并假定壓氣機等熵效率、燃燒室燃燒效率和透平等熵效率保持不變且均為額定效率值.

表1　GE MS6001FA型燃氣輪機額定工況下的性能參數

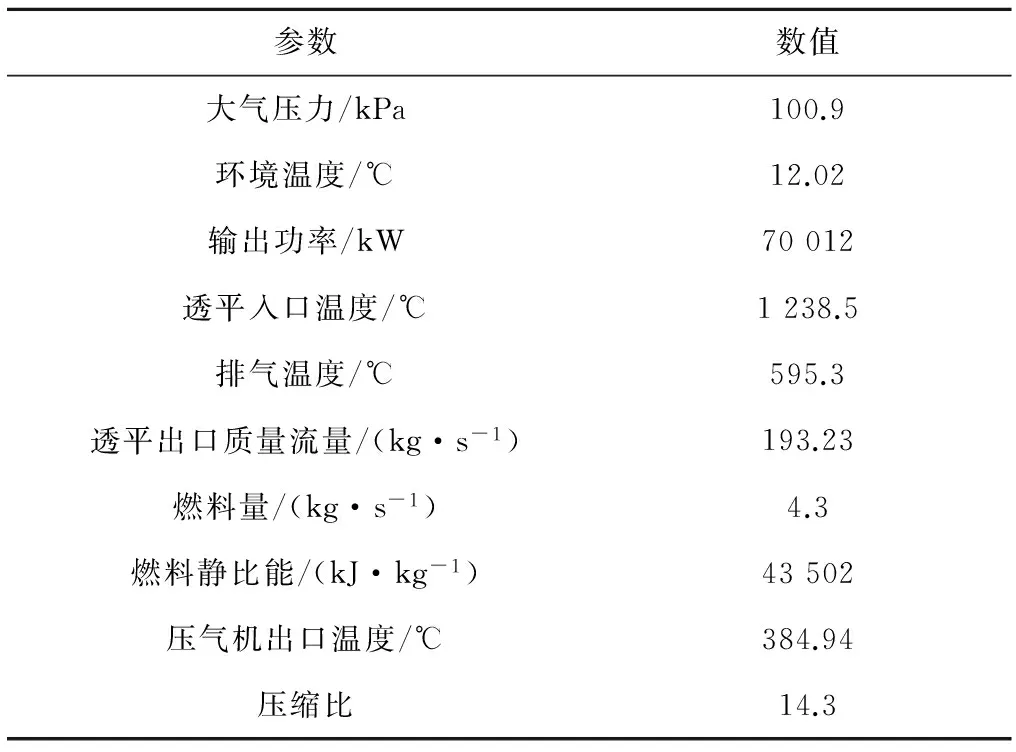
表2　燃氣輪機的現場運行數據

關于壓氣機等熵效率和透平等熵效率，首先假定燃燒室總壓恢復系數ζb=0.96，利用表2中數據、式(3)和式(4)，可得壓氣機和透平等熵出口溫度T2s(w)和T4s(w)：

(22)

(23)

式中：下標(w)表示對應表2中該燃氣輪機運行值.

利用式(1)和式(22)計算可得ηc=0.87.

同理，基于表2中的數據，利用式(2)和式(23)計算可得ηt=0.89.

由式(14)計算可得F3=-11 308.23.

由式(15)可得

(24)

考慮到額定工況下轉速偏差為0且Qd=1，式(12)可簡化為

(25)

將F3和F4代入式(30)可得qm,fd=4.64 kg/s，F4=87 178.23.

再由qm,fd和式(10)計算可得F1=457.40.

基于前文分析可知，系數F2和F5分別為

(26)

(27)

至此，模型相關系數F1、F2、F3、F4和F5均可通過計算得到.

關于重型燃氣輪機，即使不帶負荷，燃氣輪機空載運行也需要相當一部分的燃料量.于是在建模中，進入燃燒室的燃料信號為2部分之和，其中一部分為常數KNL，另一部分為(1-KNL)與控制系統輸出信號的乘積.如圖3所示，控制系統輸出要經過一個限幅器L，其最大值Lmax限制燃料過量，防止透平超溫；其最小值Lmin為負值，反映透平吸收瞬時功率的能力(逆功率情況).基于表3中燃氣輪機空載和最小燃料量數據，計算KNL和Lmin：

(28)

(29)

而Lmax一般為額定燃料量的1.5倍左右，即Lmax=1.5.

表3燃氣輪機空載燃料量和最小燃料量

Tab.3No-load and minimum fuel flow of the gas turbine

kg/s

注：1) 燃氣輪機空載(不帶負荷全速運行)和最小(保證不熄火)燃料量是從現場運行數據中提取和推算出來的，“～”表示推算值.

關于燃料管路系統容積特性，計算其容積延遲時間參數Dv1.首先，基于表4中數據，假設該溫度下存在一較小壓力波動，并結合理想氣體狀態方程，根據式(20)可得

(30)

表4　燃料系統相關數據

利用式(18)和式(19)可得Dv1=0.67s.

同理，關于燃燒室及透平的容積特性，計算燃氣量變化延遲時間參數Dv2.基于表5中數據，利用式(20)可得

(31)

利用式(18)和式(19)可得Dv2=0.43 s.

根據熱電偶式傳感器的結構參數測量燃氣輪機排氣溫度，可以確定式(21)中參數Dt1和Dt2；根據實際傳感器的響應時間，可以確定熱電偶式傳感器延遲參數Dt3.在本文中，選取Dt1=0.85、Dt2=12.2和Dt3=1.7.

表5　透平燃氣相關數據

圖3中所示的燃氣輪機控制系統數學模型的相關參數可根據實際控制系統的參數設置得到，具體見表6.

表6　控制系統數學模型參數

注：1)GS1=1/δ，δ為轉速調節系統的不等率，取δ=4%.

4　仿真結果與分析

在Matlab/Simlink環境下，基于圖3和以上分析得到的模型參數，建立GE MS6001FA型燃氣輪機系統模型來模擬其動態特性.下面給出燃氣輪機在30%基本負荷(即PL=0.3PTd)下加、減負荷的動態變化情況.首先，基于不等率δ=4%，設定轉速基準Nstd的變化曲線(見圖8).由圖8可知，模擬過程如下：仿真開始50 s內，燃氣輪機運行在30%基本負荷下；在50～110 s內加負荷到100%基本負荷，并運行至150 s；在150～170 s內減負荷到70%基本負荷，并運行至210 s；在210～260 s內減負荷到50%基本負荷，運行直至仿真結束.

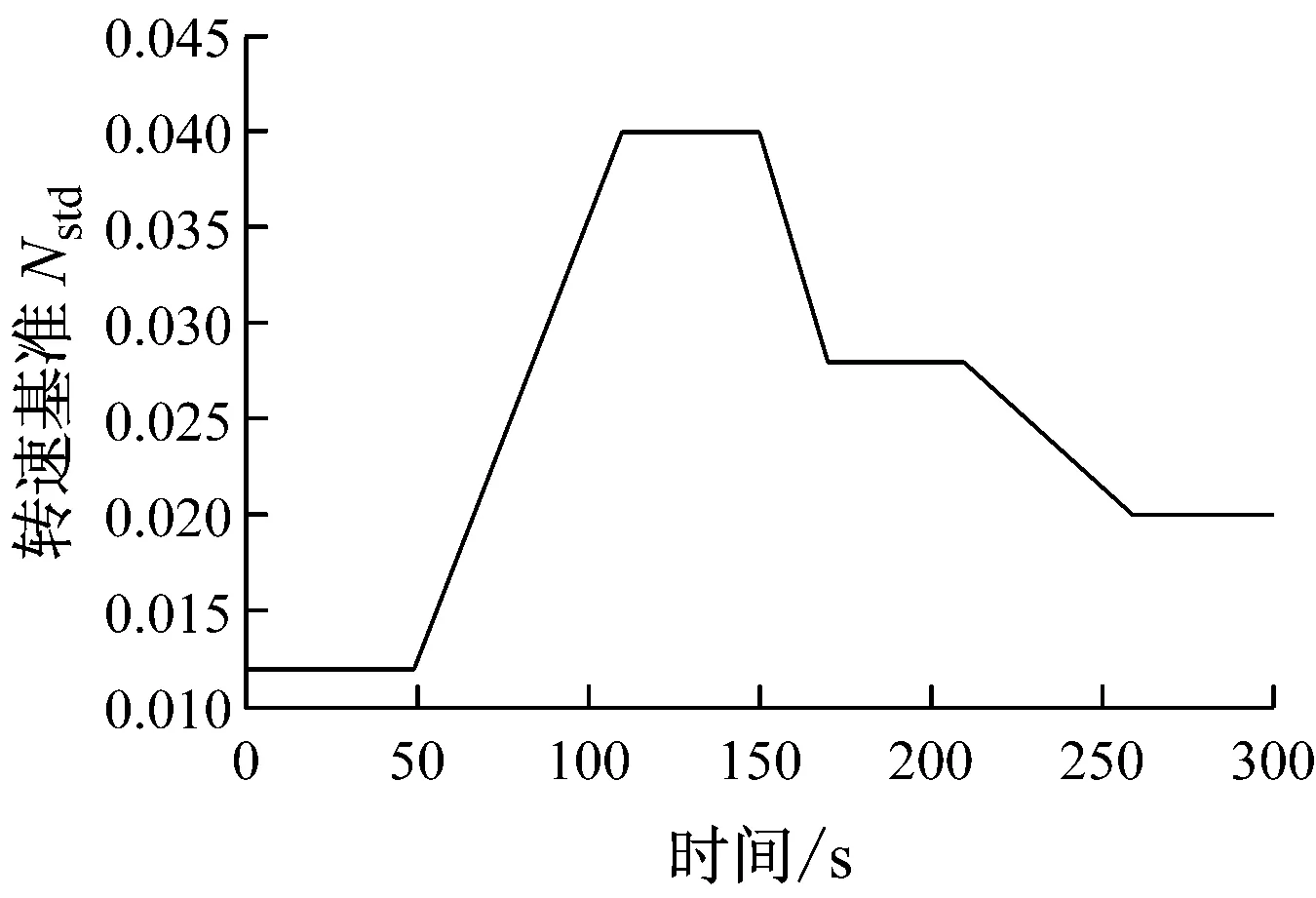
圖8　轉速基準Nstd曲線

圖9～圖11給出了燃氣輪機加、減負荷過程的模擬結果.由圖9～圖11可知，隨著轉速基準Nstd的升、降變化(模擬加、減負荷過程)，燃氣輪機排氣溫度T4、輸出功率PT和燃料量qm,f都隨之升、降，這與實際過程的變化趨勢吻合.

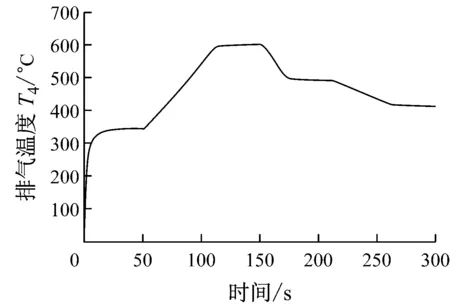
圖9　排氣溫度T4變化曲線

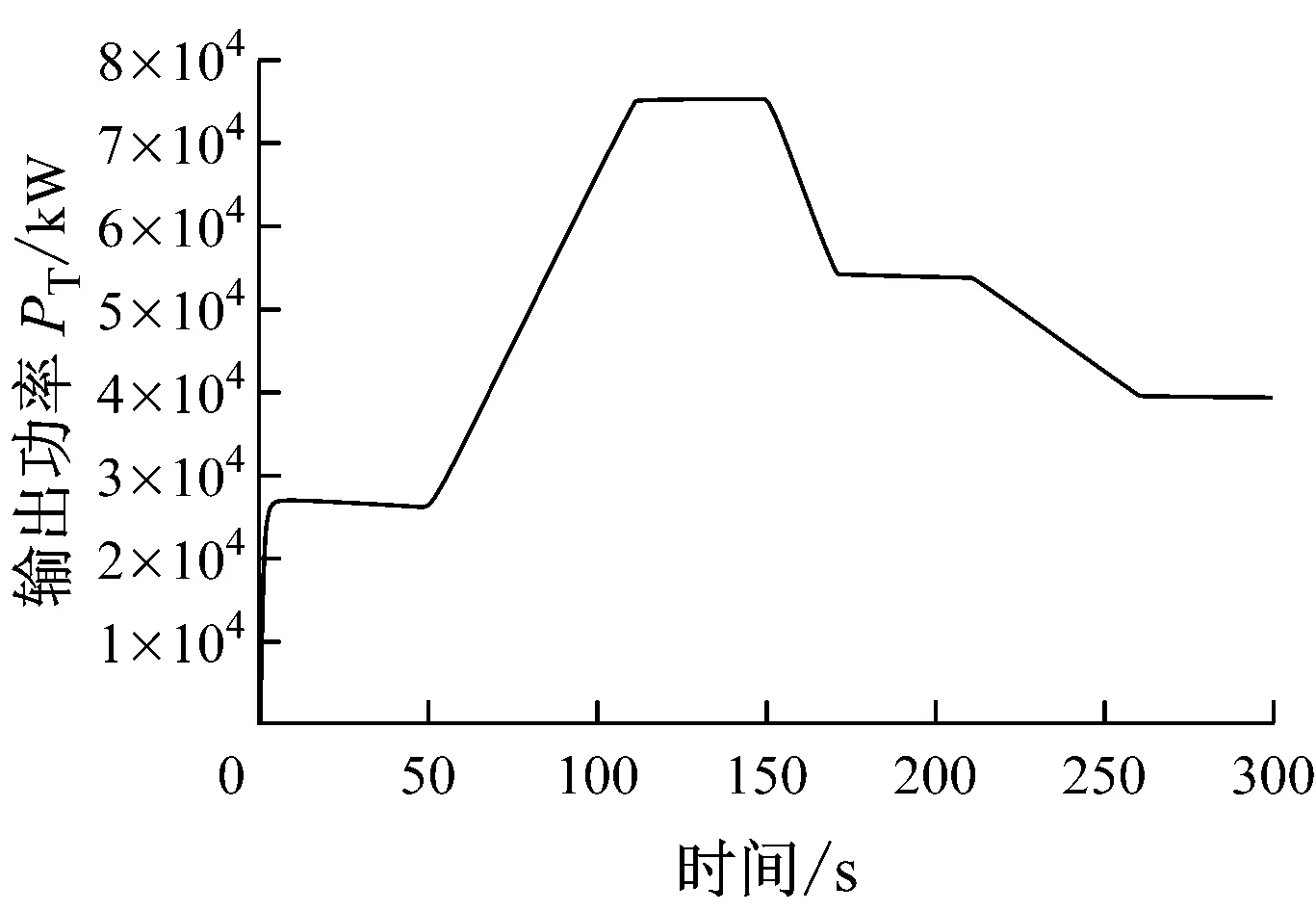
圖10　輸出功率PT變化曲線

為了進一步驗證燃氣輪機系統模型，在該系統中，將-0.3%額定轉速(即-0.3%nd)加到額定轉速下進行測試，如圖3所示.相關測試結果如圖12和圖13所示.由圖12和圖13可知，加入-0.3%nd的轉速擾動(約60 s時)后，溫度控制介入并減少燃料量qm,f，從而降低排氣溫度T4，保護燃氣輪機免受高溫損害，這與實際情況相符合.

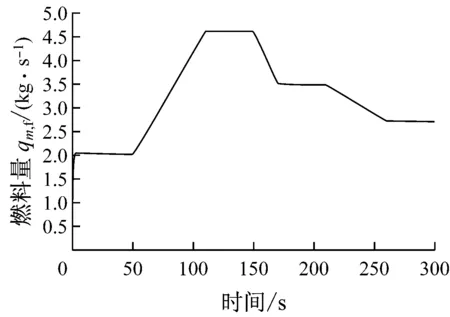
圖11　燃料量qm,f變化曲線

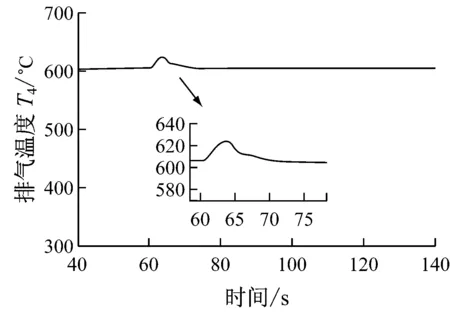
圖12　排氣溫度T4變化曲線(-0.3%nd)

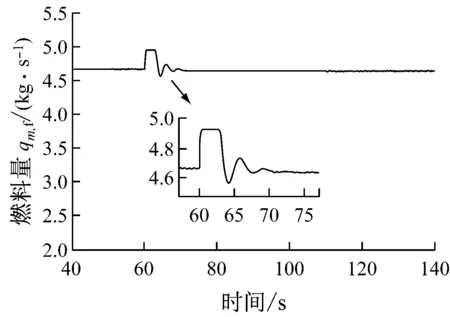
圖13　燃料量qm,f變化曲線(-0.3%nd)

5　結　論

基于Rowen模型，建立燃氣輪機及其控制系統的數學模型，并利用機組現場運行數據，對模型相關參數進行估計.同時，以GE MS6001FA型燃氣輪機為研究對象，給出燃氣輪機建模及參數估計的具體方法和過程，并進行了相關仿真實驗.仿真結果表明，該模型能夠正確再現燃氣輪機加、減負荷等工況，且符合燃氣輪機實際運行規律，具有一定的研究和參考價值.

[1]蔣洪德. 加速推進重型燃氣輪機核心技術研究開發和國產化[J].動力工程學報，2011，31(8)：563-566.

JIANG Hongde. Promote heavy duty gas turbine core technology development and industrial application in China[J]. Journal of Chinese Society of Power Engineering, 2011, 31(8): 563-566.

[2]付云鵬，黃宜坤，張會生，等. 一種考慮變幾何特性的重型燃氣輪機建模方法[J].動力工程學報，2014，34(3)：200-204.

FU Yunpeng, HUANG Yikun, ZHANG Huisheng,etal. A modeling method for heavy gas turbines considering variable geometry characteristics[J]. Journal of Chinese Society of Power Engineering, 2014, 34(3): 200-204.

[3]韋思亮，劉尚明，倪維斗. 有差調節系統燃氣輪機在Matlab/Simulink中的實現[J].動力工程，2001，21(6)：1555-1559.

WEI Siliang, LIU Shangming, NI Weidou. Simulation of gas turbine with droop control system under Matlab/Simulink[J]. Power Engineering, 2001, 21(6): 1555-1559.

[4]魏靜，陳艷軍，張建國. 聯合循環電站燃氣輪機控制系統的建模研究[J].燃氣輪機技術，2011，24(1)：45-50.

WEI Jing, CHEN Yanjun, ZHANG Jianguo. Research on modeling of gas turbine control system in combined cycle power plant[J]. Gas Turbine Technology, 2011, 24(1):45-50.

[5]鄔健，余又紅，賀星. 幾種典型燃氣輪機控制模型的比較和分析[J].燃氣輪機技術，2015，28(2)：44-49.

WU Jian, YU Youhong, HE Xing. Comparison and analysis of several typical gas turbine control models[J]. Gas Turbine Technology, 2015, 28(2):44-49.

[6]劉尚明，李忠義. 基于SIMULNK的單軸重型燃氣輪機建模與仿真研究[J].燃氣輪機技術，2009，22(3)：33-39.

LIU Shangming, LI Zhongyi. Modeling and simulation of single shaft heavy duty gas turbine using SIMULINK[J]. Gas Turbine Technology, 2009, 22(3):33-39.

[7]ROWEN W I. Simplified mathematical representations of heavy-duty gas turbines[J]. ASME Journal of Engineering for Power, 1983, 105: 865-869.

[8]ROWEN W I. Simplified mathematical representations of single shaft gas turbines in mechanical drive service[C]//ASME 1992 International Gas Turbine and Aeroengine Congress and Exposition. Germany: American Society of Mechanical Engineers, 1992.

[9]YEE S K, MILANOVIC J V, HUGHES F M. Overview and comparative analysis of gas turbine models for system stability studies[J]. IEEE Transactions on Power Systems, 2008, 23(1): 108-118.

[10]TAVAKOLI M R B, VAHIDI B, GAWLIK W. An educational guide to extract the parameters of heavy duty gas turbines model in dynamic studies based on operational data [J]. IEEE Transactions on Power Systems, 2009, 24(3): 1366-1374.

A Modeling Method for Heavy Duty Gas Turbines and the Parameters Estimation

HUANGYuzhu,JIANGHongde

(National Research Center of Gas Turbine and IGCC Technology, Tsinghua University,Beijing 100084, China)

To study the dynamic characteristics of a gas turbine, models of the gas turbine and its control system were developed based on Rowen model, while the model parameters were estimated with field data according to the laws of mass, momentum and energy conservation using basic thermodynamic formulas. Taking the GE MS 6001FA gas turbine as an object of study, specific modeling way of the gas turbine was described in detail, including its parameters estimation. Results show that the model developed can effectively reflect the dynamic characteristics conforming to actual operating rules of the gas turbine, which therefore may serve as a reference for study of similar gas turbines.

gas turbine; Rowen model; parameters estimation; field data

2015-06-03

2015-11-30

中國博士后科學基金資助項目(2014M560974)

黃玉柱(1985-)，男，河北石家莊人，博士，主要從事火電機組建模、控制與優化等方面的研究.電話(Tel．)：13401146281；

E-mail：hyzweed@163.com．

1674-7607(2016)08-0600-08

TK47

A學科分類號：470.30