三角形內外角平分線定理在數學解題中的妙用

江西省萍鄉市上栗中學　(337009)

肖　鋒

?

三角形內外角平分線定理在數學解題中的妙用

江西省萍鄉市上栗中學(337009)

肖鋒

三角形內外角平分線性質定理：

三角形的內外角平分線內、外分對邊與其延長線所得的兩條線段與夾這個角的兩邊對應成比例.

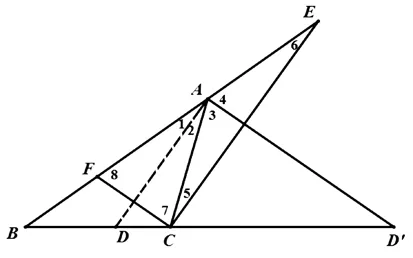
圖1

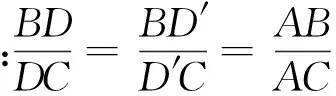
從上述推證過程，我們不難發現，這個定理的逆定理也是成立的，而且AD⊥AD′，不知出于何種原因，這一十分有趣的定理在現行教材中已蹤影全無，然而本定理所產生的重要結論，對于目前高中數學解題實踐，有著十分重要的作用.

(1)求橢圓的標準方程；

(2)點P是橢圓C上除長軸端點外的任一點，連接PF1,PF2，設∠F1PF2的角平分線PM交C的長軸于點M(m，0)，求m的取值范圍.

(3)略.

(2)命題組提供的標準答案，計算十分復雜，現引錄如下：

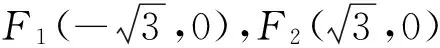
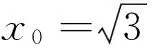
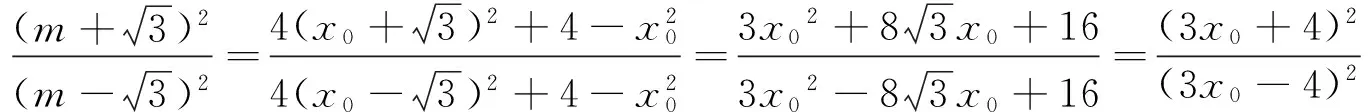
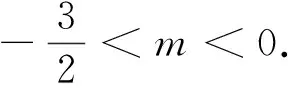
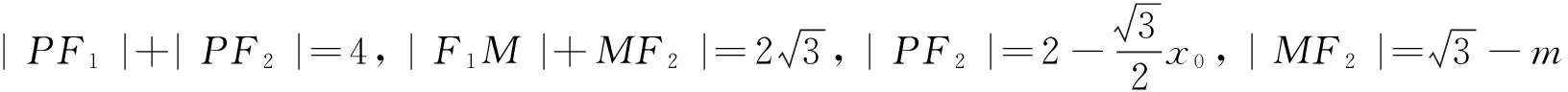
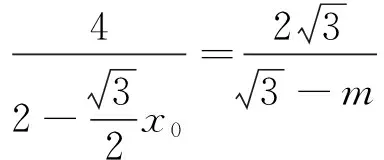
下面我們將其推廣到一般情形.

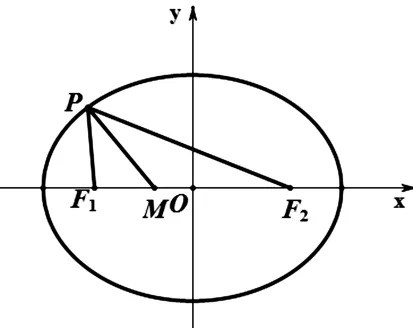
圖3

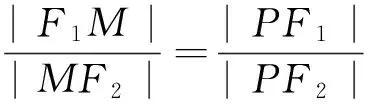
e|PF2|?e(a-ex0)=c-m?m=e2x0，由x0∈(-a，a)，知m∈(-ae2，ae2)，這里的e表示橢圓的離心率.

循著這個思路，我們來探討一下雙曲線的類似情形.

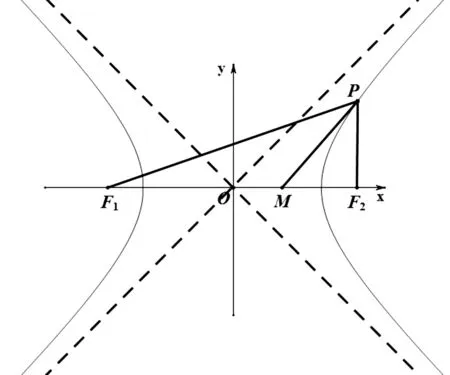
圖4

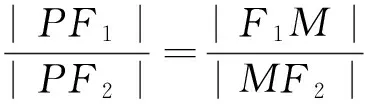
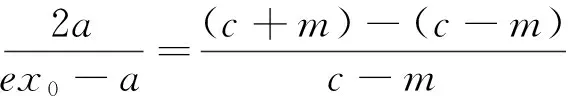
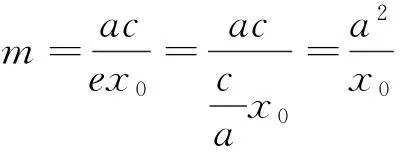
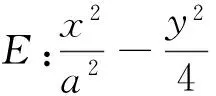
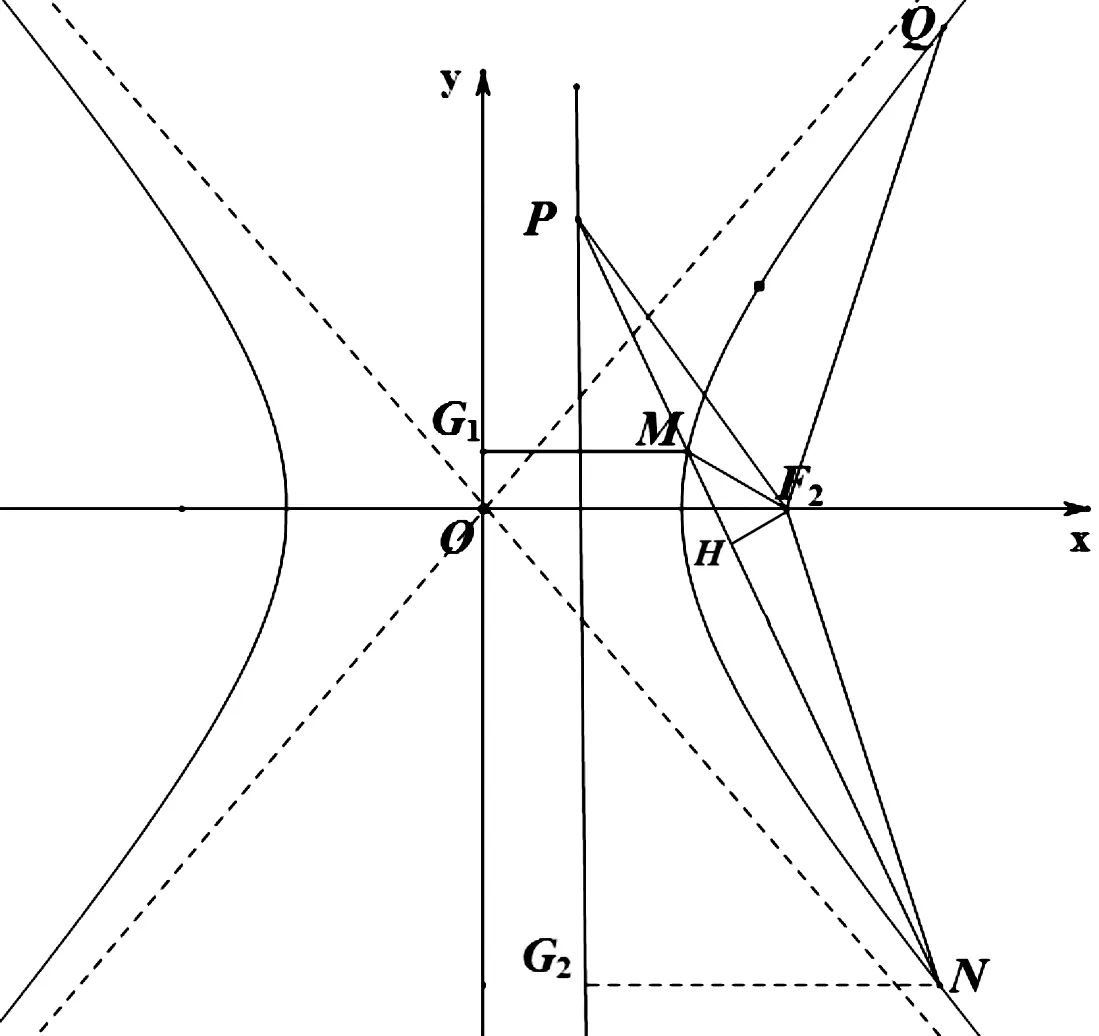
圖5

(1) 求實數a的值，并證明PQ與OQ連線的斜率之積是定值；

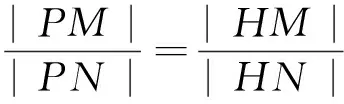
對于本題的第2問，我們先欣賞一下原創題的標準解法：

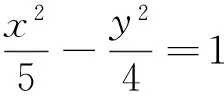
由①×③，②×④得

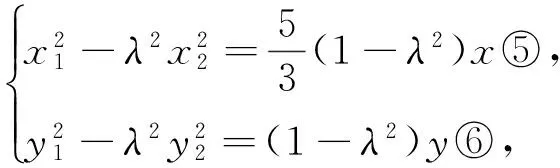
從上述解法可以看到，構思之精巧，運算之難對于一個過分依賴于計算器的當代高中生來說，只能是望而興嘆.下面筆者介紹一種解法，運用三角形內外角平分線性質定理及逆定理，將此題輕松拿下.

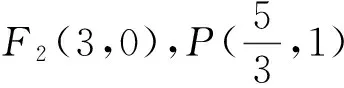
上述結論還可以推廣到雙曲線的一般情形.

值得我們注意的是此類問題對于其它圓錐曲線同樣適用.

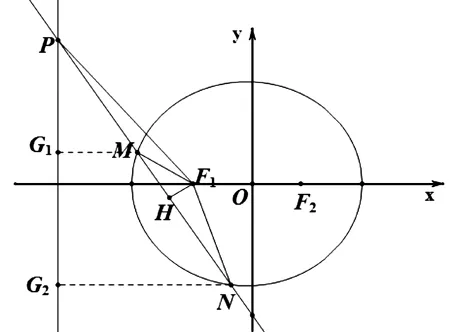
圖6

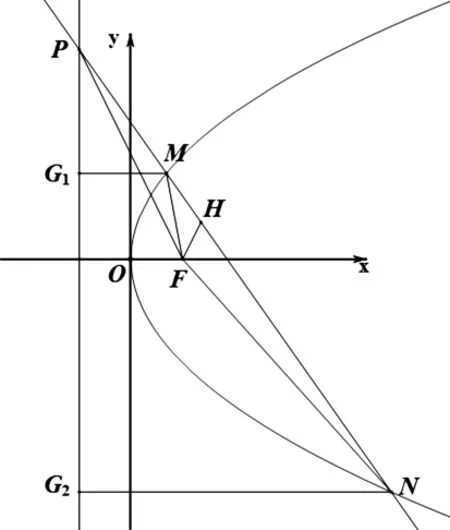
圖7

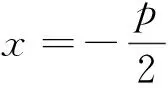
三角形內外角平分線性質定理，雖然現在初高中教材都不將其列于其中，但由于此定理形式美觀，可廣泛應用于“折直”比例置換，顯然在高中數學解題中有著重要作用，望讀者切勿輕視.