微積分及其在生活中的應用
葛家寶
吉林市廣播電視大學,吉林 吉林 132022
?
微積分及其在生活中的應用
葛家寶*
吉林市廣播電視大學,吉林吉林132022
微積分在近代工業、科研等方面發揮著重要作用。特別是微積分的創建為近代數學的發展起到了很大的推動作用,它是近代數學進一步發展和拓展的重要基礎。本文從微積分的創建、定義、以及在生活中的應用等方面剖析微積分的起源、內涵與它的重要作用。
微積分;近代數學;應用
一、微積分的早期以及創立
微積分(Calculus)目的在于研究微分、積分等問題的概念以及應用這一知識解決實際問題。微積分的應用主要是在函數與極限方面的應用。主要是將變化的不可直接計算的量微分成可計算的,求出結果再將結果積分起來。積分學,在求體積面積等方面有非常典型的應用。
微積分的創建并非是一時之工,由上文的敘述可知,它建立的基礎是很多極限思想的形成。它的極限思想更多得表現在求面積、求體積。尤其是對曲線斜率的求法,它的微分極限思想更是充分得表現。如果把新設的點沿著函數的圖象慢慢向那個點逼近,當無限逼近的時候就得到函數圖象的切線,這就是微分。
二、微積分的應用
(一)微積分在求不規則體積方面的應用
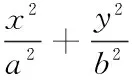
同樣,根據第一個類型的思路即可將第二種旋轉方式用類似的方法求出。即:
(二)微積分在求平面圖形的面積的計算
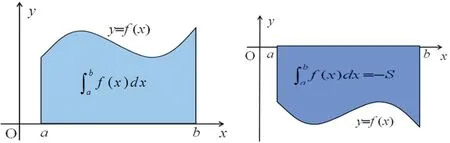
當f(x)≤0時,由y=f(x)、x=a、x=b與x軸所圍成的曲邊梯形位于x軸的下方。
牛頓——萊布尼茨公式

運用微積分知識求下列積分:


在日常生活中有很多地方要應用到面積計算問題,下面就是幾個不規則圖形面積計算的相關題目。
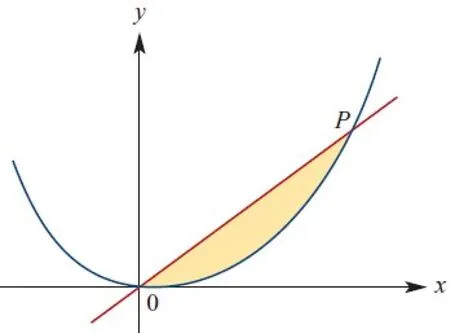
3.求曲線方程y=x2以及曲線方程y=2x所圍成的區域面積。
解:先求出P點坐標。
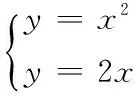
∴P點的坐標是(2,4)。

三、總結
微積分在當今生活運用之廣泛,使得人們對微積分越來越重視,在各類理工專業的學習上,微積分都是不可缺少的一類工具。不僅如此,微積分的思想在哲學方面的貢獻也不容忽視,他對立統一的思想非常契合唯物辯證法的觀點。它先微分后積分的方法使得很多不容易計算的問題變得容易解決,很多需要嘗試性試探的問題可以直觀處理。
[1]馬國良. 微積分發展淺議[J]. 云南財貿學院學報, 2000, 2:45-47.
[2]祁衛紅,羅彩玲. 微積分學的產生和發展[J]. 山西廣播電視大學學報, 2003(02).
[3]馬建珍.反例在數學分析中的作用[J].宜賓學院學報,2006,6(12).
葛家寶(1984-),男,漢族,吉林德惠人,本科,吉林市廣播電視大學,講師,研究方向:高等數學、經濟數學基礎、微積分初步。
V249
A
1006-0049-(2016)17-0253-01

