可數(shù)半連續(xù)格的序同態(tài)

周　莉，姜廣浩，周　玲（.淮北師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院，安徽 淮北 35000；.崇陽縣第一中學(xué)，湖北 咸寧 437500）

ZHOU Li1，JIANG Guanghao1，ZHOU Ling2（1.School of Mathematical Science，Huaibei Normal University，Huaibei 235000，Anhui Province，China；2.Chongyang No.1 Middle School，Xianning 437500，Hubei Province，China）

可數(shù)半連續(xù)格的序同態(tài)

周莉1，姜廣浩1，周玲2
（1.淮北師范大學(xué) 數(shù)學(xué)科學(xué)學(xué)院，安徽 淮北 235000；2.崇陽縣第一中學(xué)，湖北 咸寧 437500）

摘要：引入半素可數(shù)極小集的概念，并研究它的若干性質(zhì)及內(nèi)部刻畫.此外，借助半素可數(shù)極小集給出可數(shù)半連續(xù)格序同態(tài)的一個(gè)內(nèi)部刻畫，推廣了相關(guān)文獻(xiàn)的結(jié)果.

關(guān)鍵詞：可數(shù)半連續(xù)格；半素可數(shù)極小集；序同態(tài)

ZHOU Li1，JIANG Guanghao1，ZHOU Ling2
（1.School of Mathematical Science，Huaibei Normal University，Huaibei 235000，Anhui Province，China；
2.Chongyang No.1 Middle School，Xianning 437500，Hubei Province，China）

1　引言與預(yù)備知識(shí)

由于Scott、Lawson、Plotkin等的重要工作，連續(xù)格及其推廣引起了人們的廣泛興趣［1-2］.文獻(xiàn)［3］基于半素理想子集系統(tǒng)，借助半素理想將way-below關(guān)系“?”推廣到了二元關(guān)系“?”，進(jìn)而引入了一種新的類型格——半連續(xù)格，推廣了連續(xù)格.此后，許多學(xué)者對(duì)半連續(xù)格進(jìn)行了深入研究，得到一系列成果.文獻(xiàn)［4］在完備格上引入了半素極小集的概念，給出了半連續(xù)格的2個(gè)序同態(tài)擴(kuò)張定理，進(jìn)而將文獻(xiàn)［2］中關(guān)于連續(xù)格的序同態(tài)擴(kuò)張定理推廣到了半連續(xù)格的情形.隨著研究的進(jìn)一步深入，文獻(xiàn)［5］借助可數(shù)定向集從另一角度推廣了連續(xù)格的概念，引入了可數(shù)連續(xù)格的概念，并且得到其與連續(xù)格很多類似的性質(zhì).文獻(xiàn)［6］借助可數(shù)定向極小集得到了可數(shù)連續(xù)格序同態(tài)的一個(gè)內(nèi)部刻畫.文獻(xiàn)［7］借助半素可數(shù)理想引入了可數(shù)半連續(xù)格的概念，討論了它的一些基本性質(zhì)，進(jìn)而推廣了半連續(xù)格與可數(shù)連續(xù)格.本研究引入半素可數(shù)極小集的概念，并研究它的若干性質(zhì)及內(nèi)部刻畫；此外，借助半素可數(shù)極小集給出可數(shù)半連續(xù)格序同態(tài)的一個(gè)內(nèi)部刻畫，推廣了文獻(xiàn)［4］和［6］中的相關(guān)結(jié)果.

定義1［5-6］設(shè)L是一個(gè)完備格，a、b∈L.如果對(duì)于L中任意一個(gè)可數(shù)定向集D，b≤sup D，存在d∈D，滿足a≤d，則稱a可數(shù)way-below b，記作a?cb.

定義2［7］設(shè)L是一個(gè)完備格，Ic?L是可數(shù)理想，若?x、y、z∈L，當(dāng)x＞y∈Ic，x＞z∈Ic時(shí)，有x＞（y＜z）∈Ic，則稱Ic為L的半素可數(shù)理想.

Rdc（L）表示所有半素可數(shù)理想構(gòu)成的集合.

定義3［7］設(shè)L為完備格，定義關(guān)系?c如下：x、y∈L，x?cy??I∈Rdc（L），當(dāng)y≤sup I時(shí)，有x∈I.

記?cx=｛y∈L|y?cx｝.

定義4［7］設(shè)L為完備格，若?x∈L，x≤sup?cx，則稱L為可數(shù)半連續(xù)格；若?x∈L，x=sup?cx，則稱L為強(qiáng)可數(shù)連續(xù)格.

命題1［7］設(shè)L是可數(shù)半連續(xù)格，則關(guān)系?c具有插入性質(zhì)，即?x、y∈L，若x?cy，則?z∈L，使得x?cz?cy.

命題2［7］若L是強(qiáng)可數(shù)連續(xù)格，則L是可數(shù)連續(xù)格.

定義5［7］設(shè)L1、L2為完備格.

（1）映射f：L1→L2稱為保半素可數(shù)理想的，若f保序，且?I∈Rd（cL1），有↓（fI）∈Rd（cL2）.

（2）映射f：L1→L2稱為保半素可數(shù)理想并的，若f保序，且?I∈Rd（cL1），有（fsup I）=sup （fI）.

定義6［7］設(shè)L1、L2為完備格，映射f：L1→L2稱為保?c的，如果?x、y∈L1，x?cy，有（fx）?c（fy）.

定義7［7］設(shè)L1、L2為可數(shù)半連續(xù)格，保序映射f：L1→L2稱為是序同態(tài)的，若f保半素可數(shù)理想并和?c關(guān)系.

2　主要結(jié)論

定義8設(shè)L為完備格，a∈L，B∈Rd（cL）.稱B 為a的一個(gè)半素可數(shù)極小集，若以下條件成立：

（1）a≤sup B；

（2）?I∈Rd（cL），若a≤sup I，則?b∈B，?i∈I，使得b≤i，即B?↓I.

命題3設(shè)L為完備格，a∈L，B∈Rd（cL），則有

（1）B是a的一個(gè)半素可數(shù)極小集?a≤sup B，且B??ca；

（2）若a存在半素可數(shù)極小集，則最大半素可數(shù)極小集為B（a）=?ca.

證明（1）設(shè)B為a的半素可數(shù)極小集，且I∈Rd（cL），a≤sup I，由定義8知，?b∈B，?i∈I，使得b≤i.又I為下集，故b∈I.因此，由定義3有b?ca. 故B??ca.

反之，設(shè)a≤sup B，且B??ca，設(shè)I∈Rd（cL），且a≤sup I.由B??ca，有?b∈B，b?ca，故b∈I，從而B?I?↓I，即B是a的半素可數(shù)極小集.

（2）若a存在半素可數(shù)極小集，由（1）可知a≤sup B≤sup?ca，故a≤sup?ca，又由（1）知?ca是a的半素可數(shù)極小集.顯然?ca是a的最大半素可數(shù)極小集.

推論1設(shè)L為完備格，a∈L.a存在半素可數(shù)極小集?a≤sup?ca.

推論2設(shè)L為完備格.?a∈L，a存在半素可數(shù)極小集?L是可數(shù)半連續(xù)格.

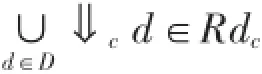
定義9映射f：X→Y稱為保半素可數(shù)極小集的，若?a∈X，當(dāng)B是a的半素可數(shù)極小集時(shí)，（fB）是（fa）的半素可數(shù)極小集.

定理1設(shè)X是可數(shù)半連續(xù)格，Y為強(qiáng)可數(shù)連續(xù)格，f：X→Y保半素可數(shù)理想，則以下條件是等價(jià)的：

（1）f保半素可數(shù)極小集.

（2）?a∈X，↓（f?ca）是（fa）的半素可數(shù)極小集.

（3）f是序同態(tài)的.

證明 （1）?（2）：由于X是可數(shù)半連續(xù)格，?a∈X，?ca是a的（最大）半素可數(shù)極小集，故↓（f?ca）是（fa）的半素可數(shù)極小集.

（2）?（3）：由條件知，?a∈X，有f（?ca）??c（fa），故f保?c.又Y為強(qiáng)可數(shù)連續(xù)格，從而（fa）= sup?c（fa）=sup （f?ca）.設(shè)I∈Rd（cX），記a=sup I，則由命題4有

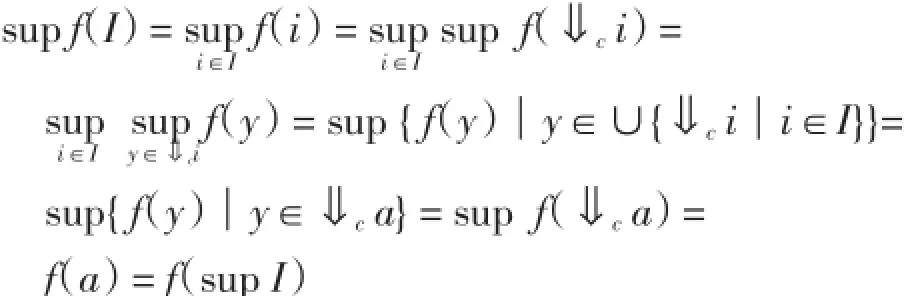
因此，f保半素可數(shù)理想并，由定義7知f為序同態(tài).

（3）?（1）：設(shè)a∈X，且B是a的半素可數(shù)極小集，則a≤sup B，且B??ca，由f保?c，有（fB）?f（?ca）??c（fa）.又f是保半素可數(shù)理想的，則有↓（fB）∈Rd（cY）.再由f是保半素可數(shù)理想并的，有sup （fB）=（fsup B）≥（fa）.故由命題3的（1），知（fB）是（fa）的半素可數(shù)極小集.

定理2設(shè)X是可數(shù)半連續(xù)格，Y是強(qiáng)可數(shù)連續(xù)格，映射f：X→Y保?c，?a∈X，令f（*a）=sup（f?ca），則f*是取值不大于f的最大的序同態(tài).

證明先證明f*是保半素可數(shù)理想并的.顯然f*是保序的，設(shè)I∈Rd（cX），記a=sup I，由命題4有

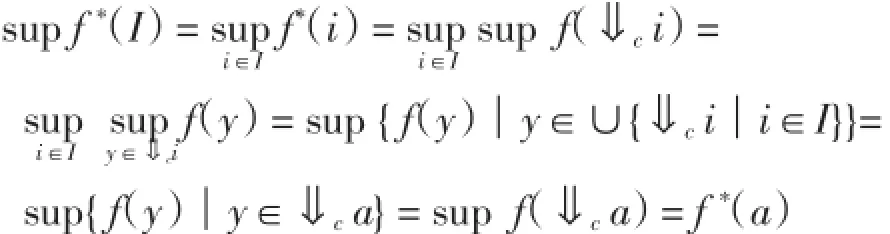
故f*保半素可數(shù)理想并.

再證明f*保?c.設(shè)a、b∈X，且a?cb.因?yàn)閄是可數(shù)半連續(xù)格，由命題1有，?z∈X，使得a?cz?cb，從而z∈?cb.又由f*的定義，有（fz）≤sup （f?cb）= f（*b），即（fz）≤f（*b）.?x∈?ca，由于f保?c，故有（fx）?c（fa）?c（fz），又Y是強(qiáng)可數(shù)連續(xù)格，由命題2 知Y是可數(shù)連續(xù)格，故（fx）?c（fa）?c（fz），即（fx）≤（fa）?c（fz），從而有

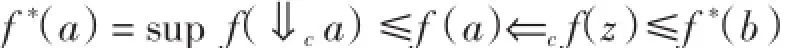
因此有f（*b）?cf（*b）.

最后證明f*是最大的.由上面的證明可知f*≤f. 設(shè)g是序同態(tài)，且g≤f，則?a∈X，有

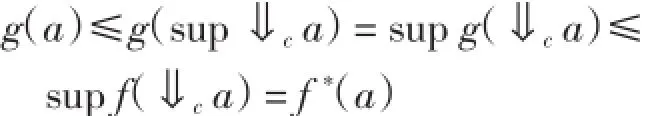
即g≤f*，這說明f*是最大的.

參考文獻(xiàn)：

［1］ GIERZ G，HOFMANN K H，KEIMEL K，et al.Continuous Lattices and Domains［M］.Cambridge：Cambridge University Press，2003.

［2］覃鋒.連續(xù)格的序同態(tài)［J］.江西師范大學(xué)學(xué)報(bào)：自然科學(xué)版，2000， 24（2）：126-130. QIN F.Homomorphisms of the continuous lattices［J］.Journal of Jiangxi Normal University:Natural Science Edition，2000，24（2）：126-130（in Chinese）.

［3］ZHAO D.Semicontinuous lattices［J］.Algebra Universalis，1997，37：458-476.

［4］康建平，徐曉泉.半連續(xù)格的半素極小集與序同態(tài)擴(kuò)張［J］.模糊系統(tǒng)與數(shù)學(xué)，2012，26（2）：142-146. KANG J P，XU X Q.Semiprime minimal sets of semicontinuous lattices and homomorphic extensions［J］.Fuzzy Systems and Mathematics，2012，26（2）：142-146（in Chinese）.

［5］陸志軍，尤飛.可數(shù)連續(xù)格與局部Lindel?f空間［J］.徐州師范大學(xué)學(xué)報(bào)：自然科學(xué)版，2008，26（3）：57-60. LU Z J，YOU F.Countable continuous lattices and local Lindel?f spaces ［J］.Journal of Xuzhou Normal University:Natural Science Edition，2008，26（3）：57-60（in Chinese）.

［6］占詩源，姜廣浩.可數(shù)連續(xù)格的序同態(tài)［J］.淮北師范大學(xué)學(xué)報(bào)：自然科學(xué)版，2014，35（2）：7-9. ZHAN S Y，JIANG G H.Homomorphisms of the countable continuous lattices［J］.Journal of Huaibei Normal University：Natural Science，2014，35（2）：7-9（in Chinese）.

［7］周莉，姜廣浩，占詩源.可數(shù)半連續(xù)格［J］.佳木斯大學(xué)學(xué)報(bào)：自然科學(xué)版，2016，34（1）：10-13. ZHOU L，JIANG G H，ZHAN S Y.Countable semicontinuous lattices［J］. Journal of Jiamusi University:Natural Science Edition，2016，34（1）：10-13（in Chinese）.

（責(zé)任編校馬新光）

第一作者：周莉（1990—），女，碩士研究生.

中圖分類號(hào)：O189.1；O153.1

文獻(xiàn)標(biāo)志碼：A

文章編號(hào)：1671-1114（2016）01-0014-03

收稿日期：2015-04-15

基金項(xiàng)目：國家自然科學(xué)基金資助項(xiàng)目（11361028，11001001）；安徽高等學(xué)校省級(jí)自然科學(xué)研究重點(diǎn)資助項(xiàng)目（KJ2013A236）.

通信作者：姜廣浩（1973—），男，副教授，主要從事一般拓?fù)鋵W(xué)方面的研究.

Homomorphisms of countable semicontinuous lattices

Abstract：The concept of semiprime countable minimal set is introduced and examined.And then its some intrinsic characterizations are given.In addition，an intrinsic characterization of homomorphisms of the countable semicontinuous lattices is obtained by semiprime countable minimal sets.These theorems generalize corresponding results in reference.

Keywords：countable semicontinuous lattice；semiprime countable minimal set；homomorphism