基于自適應EKF的BDS/GPS精密單點定位方法

趙　琳, 張勝宗, 李　亮, 王　雪

(哈爾濱工程大學自動化學院, 黑龍江 哈爾濱 150001)

?

基于自適應EKF的BDS/GPS精密單點定位方法

趙琳, 張勝宗, 李亮, 王雪

(哈爾濱工程大學自動化學院, 黑龍江 哈爾濱 150001)

為使精密單點定位(precise point positioning,PPP)獲得更短的收斂時間和更高的定位精度,多個導航系統的集成(例如北斗衛星導航系統(Beidou navigation satellite system,BDS)與全球定位系統(global positioning system,GPS)的組合)和更優的定位方法是兩種可行選擇。針對傳統最小二乘(least square,LS)法解算孤立各歷元觀測量之間的關系以及擴展卡爾曼濾波(extended Kalman filter,EKF)解算先驗信息不準的問題,在PPP中,運用自適應擴展卡爾曼濾波(adaptive extended Kalman filter,AEKF)對過程噪聲進行調整,以達到對系統狀態的最優估計。文章通過實測數據對算法進行了分析和驗證,測試結果表明,與傳統的EKF算法相比,基于AEKF算法的PPP收斂速度可提高9 min,定位精度可提高33.7%。

精密單點定位; 收斂時間; 定位精度; 自適應擴展卡爾曼濾波

0　引　言

精密單點定位(precise point positioning,PPP)技術指針對單臺接收機的載波相位觀測值,分別利用國際GNSS服務(international GNSS service,IGS)所發布的精密衛星軌道與精密衛星鐘差等產品,以及其他誤差修正模型對多種主要誤差源進行改正來實現絕對定位的方法[1]。

目前PPP技術應用較為廣泛,基于偽距與載波相位觀測數據,其靜態數據最終定位結果達到厘米級[2],相關技術已經比較成熟。文獻[3]利用9個參考站模擬基于北斗的動態定位,其結果顯示僅利用北斗系統的PPP，其定位精度可以達到分米級。但是,目前針對北斗衛星導航系統(Beidou navigation satellite system,BDS)與全球定位系統(global positioning system,GPS)組合的PPP研究相對較少,組合BDS/GPS系統進行PPP,不僅能夠增加觀測衛星數,提高量測冗余度,而且,較之單一系統,組合系統定位的可靠性、連續性、精度都有了顯著的改善。隨著全球導航衛星系統(global navigation saiellite system,GNSS)的現代化進程,雙系統甚至多系統聯合定位已經成為一種趨勢。通過組合可以充分發揮各系統的優勢,解決單系統在觀測條件不佳時可用衛星數不足的問題,以提高定位的連續性[4]。

最小二乘(least square,LS)和擴展卡爾曼濾波(extended Kalman filter,EKF)是實現PPP兩種傳統的方法,其中傳統的LS解算方法,算法簡單有效,但由于忽略了各歷元之間的關系,尤其是在高采樣率的條件下,短時間內空間信號誤差存在較強的相關性[5]。由于忽略了歷元之間的相關信息,傳統LS方法需要更長的時間完成定位收斂的過程。卡爾曼濾波是在線性無偏最小方差估計原理下推出的一種遞推濾波方法[6]。然而,傳統基于EKF的PPP方法大都采用經驗模型設置濾波先驗狀態誤差協方差陣[7-8],實際在動態定位的情況下,先驗信息很難與真實的導航狀態相匹配,導致定位需要很長的時間才能收斂。而在自適應擴展卡爾曼濾波(adaptive extended Kalman filter,AEKF)算法中,對過程噪聲和量測噪聲的估計可以優化濾波算法的性能。系統過程噪聲和量測噪聲作為系統的主要先驗信息,對卡爾曼濾波的估計性能和穩定性有著重要的意義,對于兩者估計不準確,可能會導致有偏估計,甚至濾波發散[6]。來源于真實量測信息的新息數據,對于卡爾曼濾波性能的評估而言具有重要的意義[9],通過新息方差對過程噪聲和量測噪聲實時估計和調整,從而更好適應外界環境變化所引起的噪聲統計特性的不一致性,使得濾波器具有更佳的收斂性能[9]。使用AEKF能夠避免先驗信息估計不準對卡爾曼濾波性能的影響,可以進一步提高PPP定位的收斂時間和精度。

由于動態導航環境對傳統卡爾曼模型的擾動,以及過程噪聲和量測噪聲的變化等因素的影響,制約了傳統卡爾曼濾波應用的普適性[10]。通過采用極大似然準則下的AEKF算法,對系統的過程噪聲進行實時的估計和調整,使得濾波器可以對于系統噪聲統計特性的變化做出最優化的適應。針對BDS/GPS組合系統,對這種自適應濾波算法進行了分析。實測計算結果證明該算法的有效性和可行性。

1　組合精密單點原理與技術分析

1.1觀測方程及誤差處理

衛星導航定位中基本的觀測方程為

(1)

(2)

式中,φ、P分別為載波相位以及測碼偽距觀測量;ρ為用戶與衛星之間真實的幾何距離;c為電磁波在真空中的傳播速度;dtr、dts分別為接收機鐘差以及衛星鐘差;I為電離層延遲誤差;T為對流層延遲;dorb為衛星軌道誤差;dtid為潮汐誤差;drel為相對論效應誤差;N為整周模糊度;dant為天線相位誤差;dphw為相位纏繞誤差;εφ為載波相位觀測噪聲和多路徑誤差;εP為偽距觀測噪聲和多路徑誤差。

實際應用中,根據電離層介質的彌散性質,采用雙頻觀測值消除電離層折射影響[11]。考慮組成L1、L2(B1、B2)頻率上的線性組合的觀測值,其組合系數α1、α2滿足:

(3)

式中,f1、f2分別為載波L1、L2(B1、B2)的頻率。原則上,α1、α2可以是任意一組滿足式(3)的值。但在實際應用中,經常選擇[12]

(4)

由此,可以利用雙頻觀測值消除電離層影響。通常使用無電離層組合(ionosphere-free,IF)觀測值,組合觀測量如下:

(5)

(6)

式中,φIF、PIF分別為無電離層組合載波相位和偽距觀測值;NIF為組合整周模糊度;νφ、νP分別為無電離層相位和偽距組合觀測噪聲,此外

(7)

(8)

式(7)和式(8)中所涉及誤差處理方法如表1所示。

表1　PPP誤差處理方法

在對各部分誤差進行處理后,可以得到修正后的IF組合載波相位觀測值和偽距觀測值:

(9)

(10)

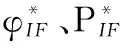
1.2參數估計方法

在上述對PPP各部分誤差進行相應的處理后,PPP的估計參數有接收機三維位置、三維速度(動態)、接收機鐘差、接收機頻漂、對流層濕分量延遲、組合模糊度。濾波處理中選取的狀態向量為

(11)

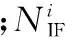
表2　狀態處理方法

選取的量測量為每顆可視衛星的IF組合載波相位與偽距觀測值:

(12)

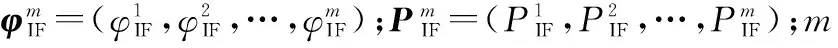
然后對系統進行建模,考慮到系統的非線性,需要先將濾波方程線性化,其中,量測方程非線性,系統模型表示為

(13)

(14)

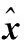
(15)

其中

(16)

其中

(17)

令

(18)

(19)

則將非線性量測函數式(14)一階線性化后得到量測方程為

(20)

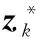
至此,可以得到線性化的系統模型式(13)和式(20),其中狀態轉移陣Φ和量測陣H可表示為

(21)

式中,I表示單位陣。靜態模式時A=03×3,B=03×3,C=[1,0;0,0];動態模式時A=TsI3×3,B=I3×3,C=[1,Ts;0,1],Ts是狀態方程的差分步長,在這里也等于測量過程的采樣時間間隔。

(22)

式中,G3×k=(lk,mk,nk)(k=1,2,…,m)表示接收機到衛星的觀測向量的方向余弦矩陣;I表示單位陣;E=[I1×m,01×m,I1×m,01×m];M1×m=(M1,M2,…,Mm)表示對流層濕分量映射函數矩陣。

在得到由精密星歷文件計算的衛星位置誤差方差,由精密鐘差文件計算的衛星鐘差誤差方差,IF組合觀測噪聲方差以及對流層誤差方差之后,可以較為準確地得到量測噪聲方差陣。此外,同時對過程噪聲和量測噪聲進行調整的AEKF算法,容易導致濾波發散及濾波過程不穩定[6]。因此，下面所推導的自適應過程僅對過程噪聲進行調整估計。

本文運用基于極大似然準則的AEKF對系統狀態進行估計,極大似然準則綜合新息以及新息協方差的變化,使其能夠適應模型擾動以及噪聲統計特性變化的影響[13]。已知系統的線性模型如式(13)和式(20)所示,基于參考文獻[6]可以計算自適應過程下的過程噪聲為

(23)

式中,N為平滑窗口寬度;Δx為狀態更正量;P為估計誤差方差陣。

2　數據處理與分析

為充分驗證所提出算法的性能,通過靜態和動態PPP實驗進行了測試。需要指出的是,測試過程中,BDS和GPS精密星歷與精密鐘差數據分別由中科院測地所和IGS中心提供,更新時間分別為15 min和5 min。

在對數據進行處理時,還應考慮各個觀測值的權重大小,權重表示了各個觀測值對整個解的貢獻大小,正確匹配權值才能獲得最優的結果,這其中涉及的以衛星高度角定權的一種隨機模型形式為

(24)

(25)

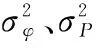
在濾波過程中,由式(23)可知在估計過程噪聲Q時涉及到Δx項,從而直接反映系統的狀態變化,由此可見,準確地估計過程噪聲將會使得濾波器更好地跟蹤動態條件系統狀態的變化情況。所以在數據處理中,必須恰當地選擇平滑窗口的寬度N,為此,測試時對N進行了不同的取值,取N從50開始,按步長50增加,通過比較分析可知,當窗口寬度N取200時,狀態估計誤差精度達到最高。

2.1靜態模式

為測試靜態條件下BDS/GPS組合系統及單系統PPP的效果,采用澳大利亞CUT0站2014年6月17日的數據進行定位解算,其接收機為Trimble Net R9,該觀測數據采樣率為30 s,截止高度角設為15°。在AEKF處理過程中,BDS和GPS載波相位觀測量的觀測噪聲標準差均設為0.003 m,偽距觀測量的觀測噪聲標準差分別設為0.6 m和0.3 m。

本文分別對BDS單系統,GPS單系統,BDS/GPS組合系統3種情況進行AEKF數據處理。以XYZ三方向的位置誤差(分別用errorX、errorY、errorZ表示)均達到10 cm以內定義濾波收斂。對BDS/GPS組合系統分別應用LS、EKF、AEKF 3種方法進行解算,得到實驗結果如圖1～圖4以及表3所示。

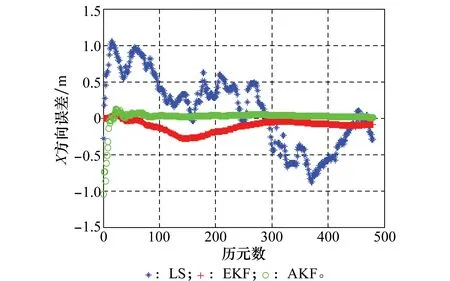
圖1　3種解算方法X方向誤差圖Fig.1　X-component error of three methods

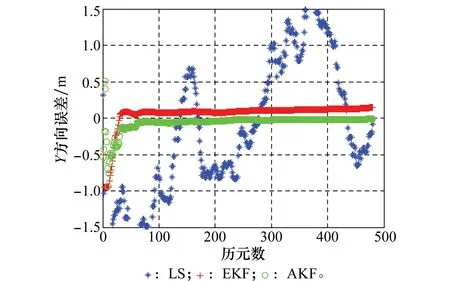
圖2　3種解算方法Y方向誤差圖Fig.2　Y-component error of three methods

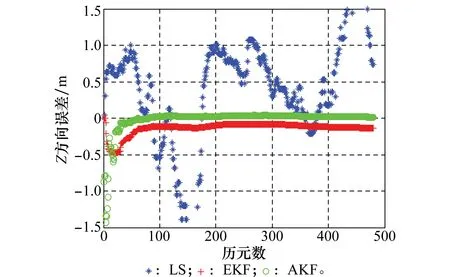
圖3　3種解算方法Z方向誤差圖Fig.3　Z-component error of three methods

對比圖1～圖3中組合系統3種解算方法的位置誤差曲線,可以看出,AEKF算法較之LS、EKF在定位精度及收斂速度方面有很大提升。LS方法由于沒有將不同時刻的定位值聯系起來相互制約,因而定位結果通常顯得相當粗糙、雜亂,無法實現收斂;EKF方法由于初值及先驗信息估計不夠準確,導致收斂時間增加,收斂后的定位精度不夠高;而AEKF方法由于通過LS方法得到了較為準確的濾波初值,濾波時間較短,定位結果較為理想。

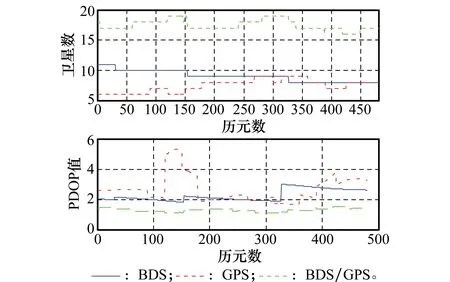
圖4　3種定位方式衛星數及PDOP值Fig.4　Numbers of satellites and PDOP value of different systems

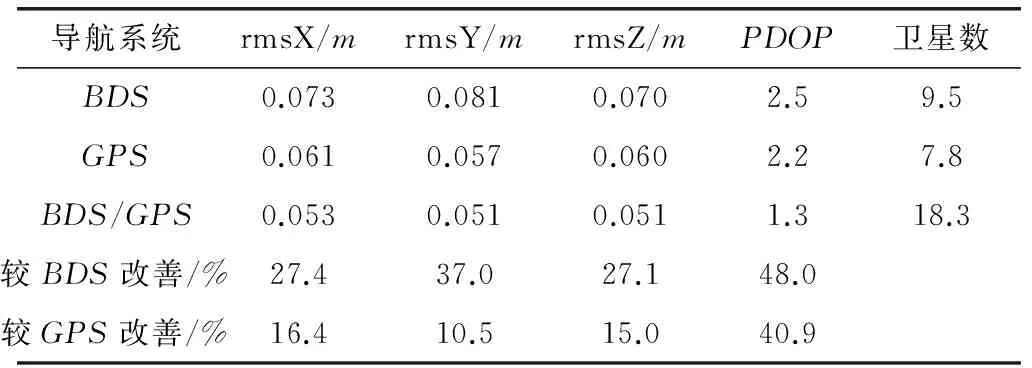
表3　BDS、GPS、BDS/GPS組合定位性能比較

對比圖4及表3可以發現,雖然在大部分時間里BDS系統的衛星數要多于GPS系統,但是定位精度因子(positiondilutionofprecision,PDOP)有時沒有GPS衛星的小,這主要是由于目前BDS系統的中地球軌道衛星較少,衛星空間結構不好造成的。目前BDS系統正處于全球組網階段,其跟蹤站數量有限,所提供的BDS衛星的精密軌道數據精度還不夠高,而PPP解的優劣與衛星軌道和衛星鐘差修正的精度有很大關系,并且,目前BDS系統只有14顆可用衛星,而GPS系統有32顆,其幾何強度要遠比BDS好。因此當前條件下BDSPPP的收斂時間明顯長于GPSPPP[7]。而BDS/GPS組合系統相較單系統來說,極大提高了可用衛星的數目,從而改善了空間衛星幾何分布。另外由圖4可以看出,組合系統對PDOP值有平滑作用,使得數據處理收斂效果較好。這也是組合系統能夠加快收斂時間的主要原因。定量分析發現,靜態條件下,BDS系統PPP的X分量大部分優于5cm,Y分量大部分優于6cm,Z分量大部分優于5cm。GPS系統PPP的X分量大部分優于3cm,Y分量大部分優于3cm,Z分量大部分優于3cm。BDS/GPS組合系統PPP的X分量大部分優于1cm,Y分量大部分優于2cm,Z分量大部分優于2cm。

GPS系統X、Y、Z 3個方向上的均方根誤差(rootmeansquare,RMS)統計均小于BDS系統,這是因為目前BDS衛星數較少,導致衛星幾何構型和可靠性較差[14]以及精密軌道和精密鐘差的精度相對較低。而BDS/GPS組合系統的衛星數目增加了約一半,衛星數目的增加使得相應的PDOP值有較大改善,定位精度可以得到明顯提高。

2.2動態模式

為進一步驗證算法在動態模式下的性能,在校園環境內開展動態試驗。基準站和移動站均采用NovAtelPP6接收機,基準站與移動站之間的距離小于1km,整個動態實驗時間約為22min,接收機運動速度較低(小于10m/s),數據采樣率為1s,截止高度角為10°,圖5為移動站運動軌跡圖。在AEKF處理過程中,BDS和GPS載波相位觀測量的觀測噪聲標準差均設為0.003m,偽距觀測量的觀測噪聲標準差分別設為0.6m和0.3m。

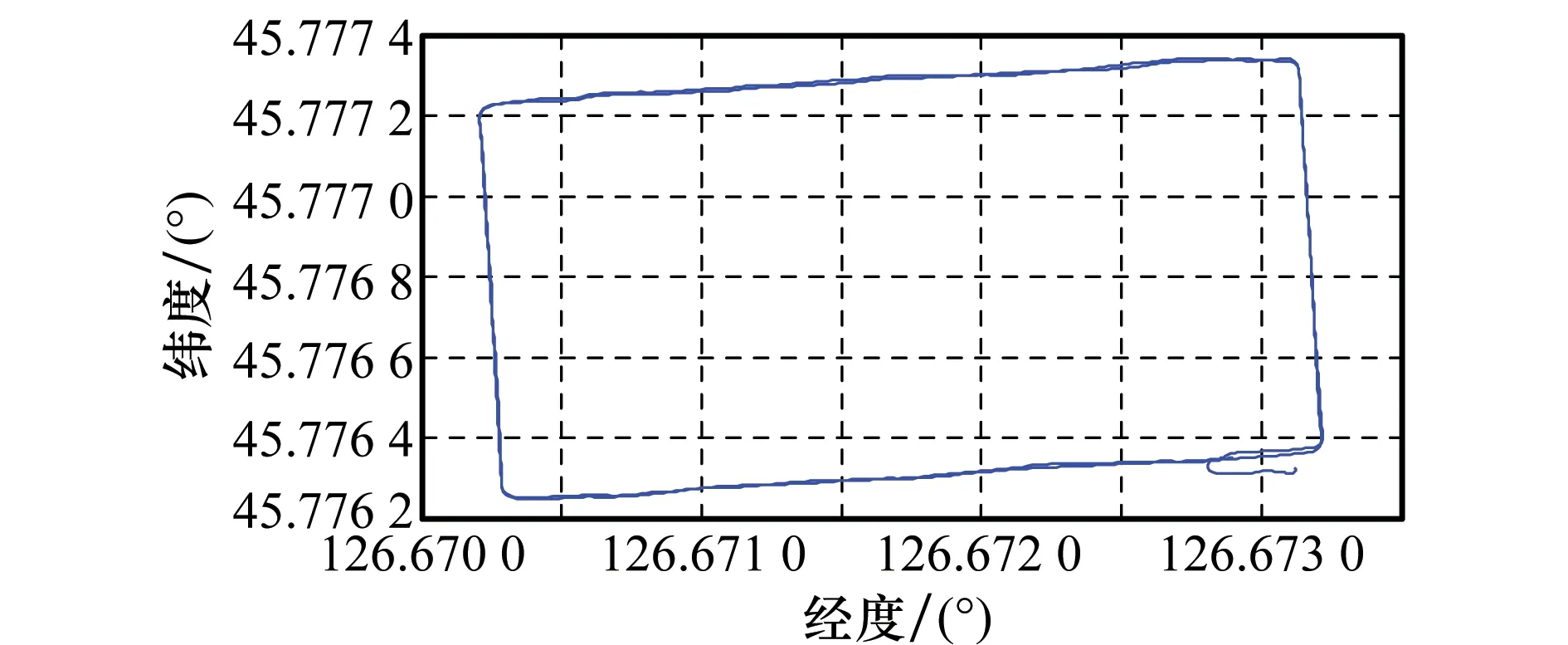
圖5　移動站運動軌跡圖Fig.5　Reference trajectory of rover user

為評估動態PPP精度,定位參考坐標來自于開源軟件包RTKlib中的雙頻載波相位差分定位技術,定位精度可達到10cm級別。

運用LS、EKF、AEKF對BDS/GPS組合系統進行解算,以及運用AEKF對BDS單系統、GPS單系統、BDS/GPS組合系統進行分析,得解算結果如圖6～圖9及表4所示。

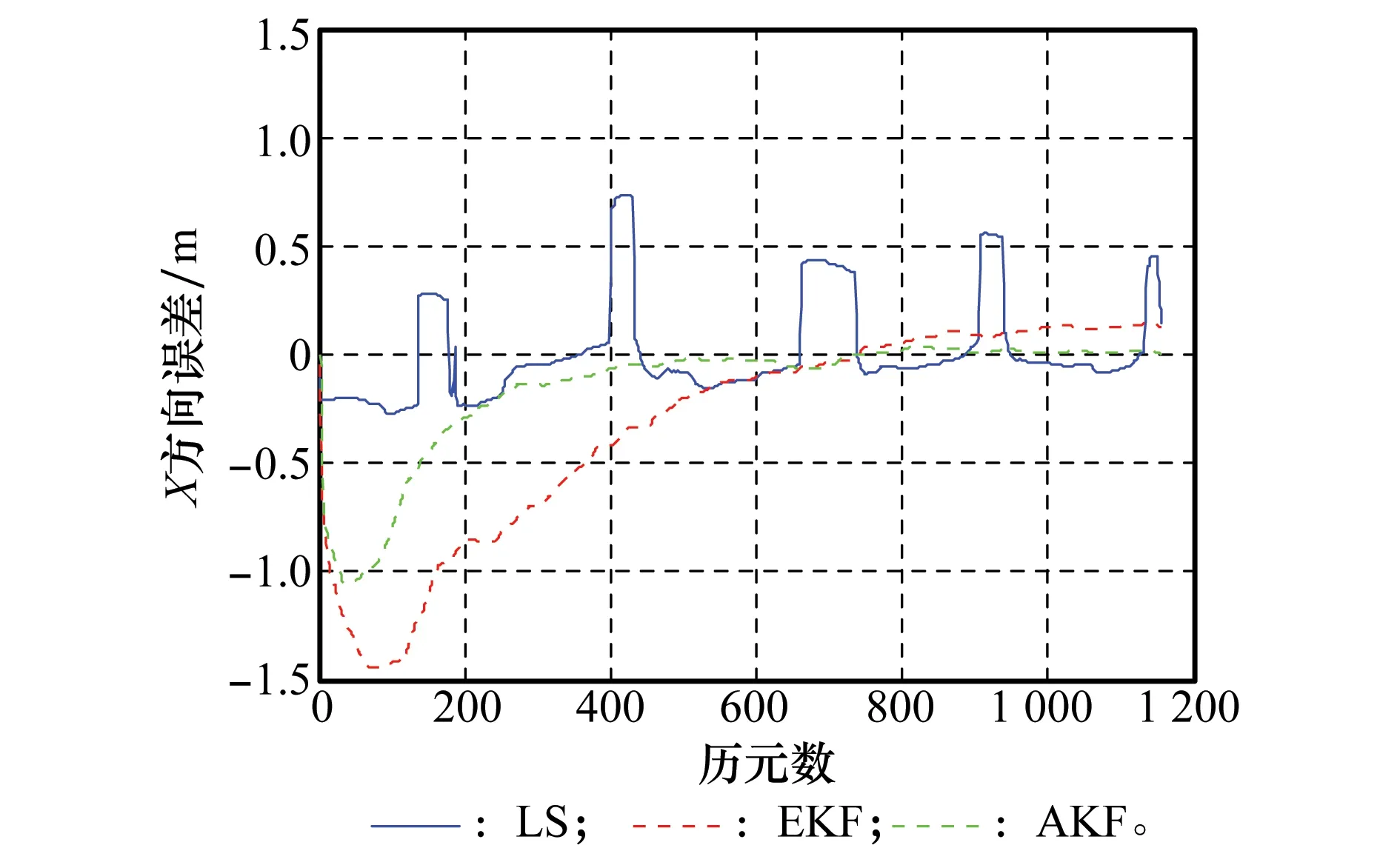
圖6　3種解算方法X方向動態誤差圖Fig.6　X-component kinematic error of three methods

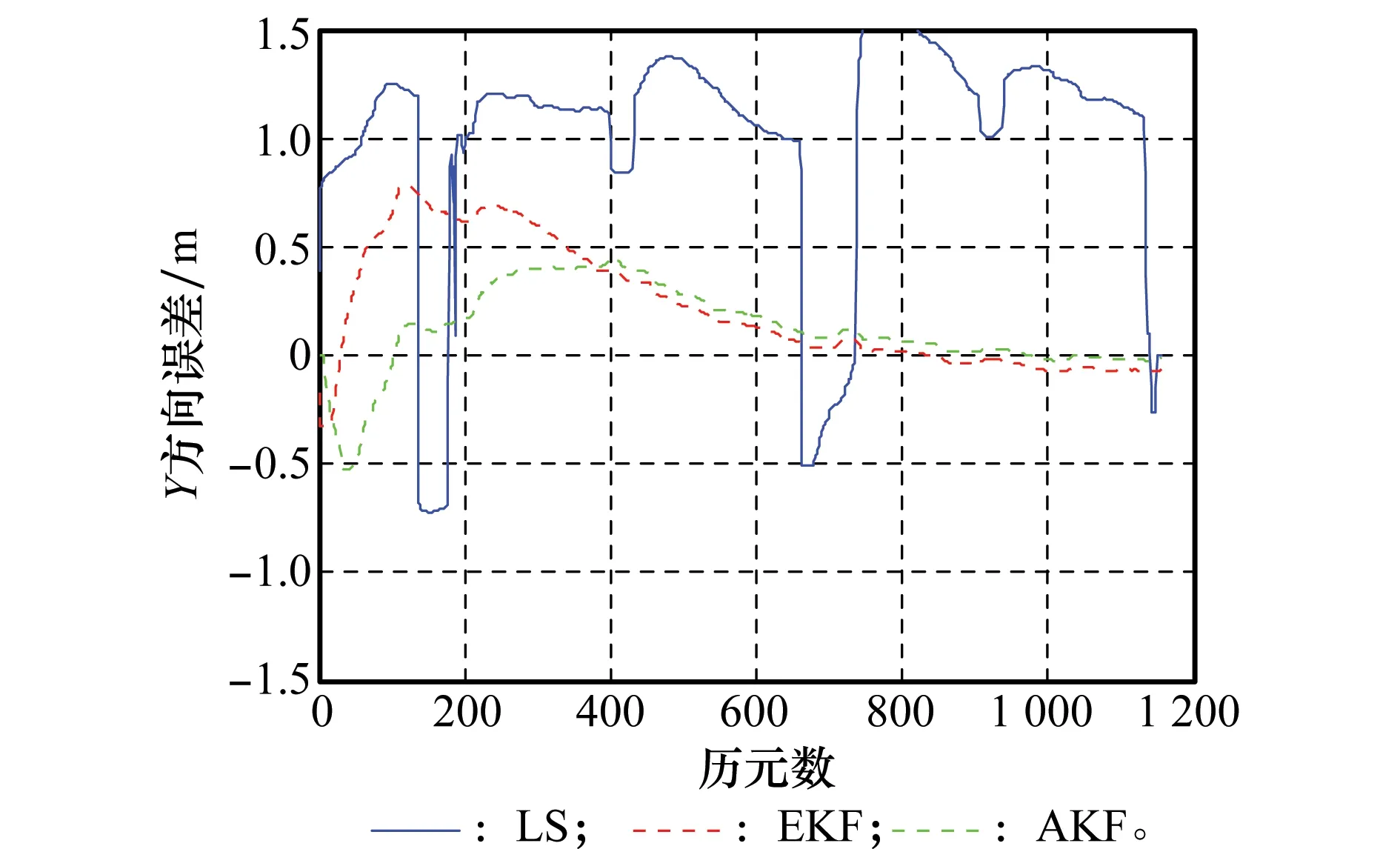
圖7　3種解算方法Y方向動態誤差圖Fig.7　Y-component kinematic error of three methods

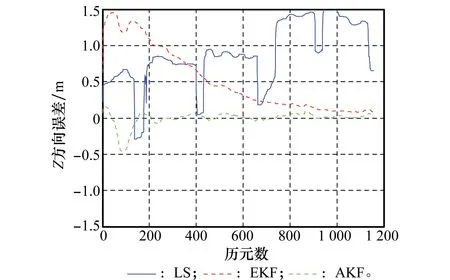
圖8　3種解算方法Z方向動態誤差圖Fig.8　Z-component kinematic error of three methods

對比圖6～圖8中組合系統3種解算方法的位置誤差曲線,可以看出,AEKF算法較之LS、EKF在定位誤差及收斂速度方面有很大提升。與靜態的情況相比,動態模式較為復雜,實際系統中,接收機的運動狀態往往是未知的,同時運動的背景環境也可能是比較復雜的。因此在動態高采樣率的情況下,LS方法由于忽略了各歷元之間的關系,各歷元定位結果之間存在突變情況,無法實現收斂,另外由圖9中PDOP值的突變,解釋了LS方法中定位誤差的突變情況;同樣地，在動態模式下,EKF對初值及先驗信息的估計準確度更為敏感,由于先驗信息估計不夠準確,使得EKF估計方法收斂時間增加,收斂后的定位結果還不夠好;AEKF的濾波初值及先驗信息由最小二乘法得到,與通過經驗值進行濾波初值設置的方法相比,本文所提AEKF算法的濾波性能相對更好,這在一定程度上彌補了運動的復雜性及高動態性,使得濾波時間相對較短,定位結果較為理想。

圖9　3種動態定位方式衛星數及PDOP值Fig.9　Satellite number and PDOP in the kinematic mode

對比圖9及表4可以發現,BDS系統的衛星個數要少于GPS系統,BDS對應PDOP值要明顯大于GPS,然而隨著BDS組網建設,將大大增加中軌道衛星的數目,因此BDS衛星的空間幾何結構將會得到有效改善。此外,BDS測距精度和信號穩定性較GPS略差[15],相應地，在定位精度上BDS系統比GPS系統要差,而BDS/GPS組合系統由于衛星數量上的提高,使得系統的幾何結構及定位可靠性增強,PDOP值相對單系統來說顯著減小,使得定位精度有較大提高。

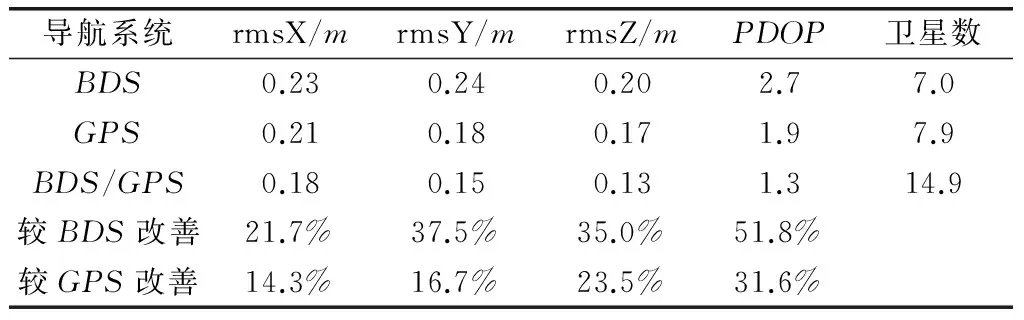
表4　BDS、GPS、BDS/GPS組合動態定位性能比較

從數值上看,組合系統對BDS系統PDOP值的改善效果要比GPS大得多,這主要是因為BDS尚不完善,衛星幾何構型還不夠好,因此導致其PDOP值較大。雖然目前BDS系統并不完善,在軌衛星較少,但是已經可以為GPS觀測提供冗余觀測量,對GPS幾何構型的改善效果是顯著的。單一的GPS或者BDS系統PDOP值在一些時刻變化較大,說明雖然該觀測時段內系統的可用衛星數平均較多,但是由于衛星分布不均勻及信號失鎖等原因,會造成單一系統定位結果不夠準確,系統組合很好地解決了這個問題。為分析濾波收斂后的定位精度和穩定性,對結果進行分析,可以發現,動態條件下,收斂之后BDS系統PPP的X分量優于11cm,Y分量優于12cm,Z分量優于6cm。GPS系統PPP的X分量優于9cm,Y分量優于10cm,Z分量優于5cm。BDS/GPS組合系統精密單點定位的X分量優于4cm,Y分量優于6cm,Z分量優于4cm。

與靜態模式相比,動態模式下,由于接收機的運動以及較高的采樣率,使得對系統狀態的估計更為困難,采用多系統組合相比單系統可以成倍地增加可視衛星數,衛星數目的增加使得相應的PDOP值有較大改善。另外,衛星數目的增加使得量測量增加,提高了量測冗余度。對比靜態模式,可以看出,動態模式下,組合系統在性能上較之單系統幅度提高更大,效果更為明顯。系統定位可靠性、連續性、精度都有了顯著的改善。因此,多系統聯合精密定位是可行的。

3　結　論

采用AEKF的方法,本文針對BDS/GPS組合PPP進行了改進研究與實現。一方面,與單系統PPP結果的對比分析發現,組合系統較單一系統在定位精度與收斂速度上都有顯著提高,而且組合系統具有更多的可用衛星,能夠保證定位的可靠性、可用性和連續性。另一方面,將AEKF應用于組合系統,相比傳統方法,組合系統性能達到最優化,對動態的適應性有很大提高。

從實驗結果來看,雖然單獨BDS系統可以實現高精度定位,但是多個衛星導航系統聯合定位,可以進一步提升精密定位的性能,本文的研究可為多個GNSS組合情況下的PPP提供一定的參考。

[1]ZumbergeJF.AutomatedGPSdataanalysisservice[J].GPS Solutions, 1999, 2(3): 76-78.

[2]ZhangXH,LiuJN,ForsbergR.Applicationofprecisepointpositioninginairbornesurvey[J].Geomatics and Information Science of Wuhan University, 2006, 31(1): 19-22.

[3]LiX,GeM,ZhangH,etal.TheGFZreal-timeGNSSprecisepositioningservicesystemanditsadaptionforCOMPASS[J].Advances in Space Research, 2013, 51(6): 1008-1018.

[4]HeF,GaoCF,PanSG.ApplicationofrobustHelmertvariancecomponentestimationinGPS/BDS/GLONASSintegratedpositioning[J].Journal of Navigation and Positioning, 2013, 1(3): 56-61.

[5]ZhaoL,LiL,SunM,etal.NoveladaptivehatchfiltertomitigatetheeffectsofionosphereandmultipathonLAAS[J].Journal of Systems Engineering and Electronics, 2010, 21(6): 1046-1053.

[6]ZhaoL,WangXX,LiL,etal. Nonlinear system filtering theory[M].Beijing:NationalDefenseIndustrialPress,2012.(趙琳,王小旭,李亮,等.非線性系統濾波理論[M].北京:國防工業出版社,2012.)

[7]ZhangXH,ZuoX,LiP.ConvergencetimeandpositioningaccuracycomparisonbetweenBDSandGPSprecisepointpositioning[J].Acta Geodaetica et Cartographica, 2015, 44(3): 250-256.

[8]MengXG,GuoJM.ResearchonGPS/GLONASSintegratedprecisepointpositioning[J].Geomatics and Information Science of Wuhan University, 2010, 35(12): 1409-1413.

[9]LiL.Groundbasedaugmentationsystempositioningandintegritymonitoring[D].Harbin:HarbinEngineeringUniversity,2012. (李亮. 陸基增強系統定位與完好性監測技術研究[D]. 哈爾濱: 哈爾濱工程大學, 2012.)

[10]SouzaMFD,LuoZQ.Finite-horizonrobustKalmanfilterdesign[J].IEEE Trans. on Signal Processing, 2001, 49(9): 2103-2112.

[11]ZhangSX. Technology and application of GPS[M].Beijing:NationalDefenseIndustrialPress, 2004. (張守信.GPS技術與應用[M]. 北京: 國防工業出版社, 2004.)

[12]YeSR.TheoryanditsGPSprecisepointpositioningusingun-differencedphaseobservation[D].Wuhan:WuhanUniversity, 2002.(葉世榕.GPS非差精密單點定位理論與實現[D]. 武漢: 武漢大學, 2002.)

[13]YueXK,YuanJP.AnadaptiveKalmanfilteringalgorithmbasedonmaximum-likelihoodcriterion[J].Journal of Northwestem Polytechnical University, 2005, 23(4): 469-474.

[14]JinB,YangSW,LiuWK.AnalysisofGPS/BDSintegratedsinglepointpositioning[J].Hydrographic Surveying and Charting, 2013, 33(4): 39-41, 65.

[15]TangWM,XuK,JinL,etal.TestandanalysisofBeidou/GPScombinedpseudorangepointpositioningperformance[J].Geomatics and Information Science of Wuhan University, 2015, 40(4): 529-533. (唐衛明, 徐坤, 金蕾, 等. 北斗/GPS組合偽距單點定位性能測試和分析[J].武漢大學學報(信息科學版), 2015, 40(4): 529-533.)

李亮(1984-),通信作者,男,講師,博士,主要研究方向為衛星導航定位與完好性監測。

E-mail:liliang@hrbeu.edu.cn

王雪(1992-),女,碩士研究生,主要研究方向為精密單點定位。

E-mail:wangxue_407@hrbeu.edu.cn

BDS/GPS integrated precise point positioning based on adaptive extended Kalman filter

ZHAO Lin, ZHANG Sheng-zong, LI Liang, WANG Xue

(CollegeofAutomation,HarbinEngineeringUniversity,Harbin150001,China)

In order to achieve the shorter convergence period and better positioning accuracy for precise point positioning (PPP), the combination of multiple navigation satellite, such as the Beidou navigation satellite system (BDS) and the global positioning system (GPS), and the better positioning method are two ways to choose. However, since the traditional least square (LS) estimator ignores the temporal correlation of observations, and the extended Kalman filter (EKF) is limited by inaccurate prior information, a novel PPP method based on adaptive extended Kalman filter (AEKF) is used to adjust the process noise with the measurement consistency test. The experiment results show that, compared with traditional EKF solution, the convergence period of PPP based on AEKF can be shorten by 9 minutes, and the accuracy of positioning can be increased by 33.7%.

precise point positioning (PPP); convergence period; positioning accuracy; adaptive extended Kalman filter (AEKF)

2015-10-14；

2015-12-21；網絡優先出版日期：2016-02-18。

國家自然科學基金(61304235，61273081, 61304234)；中央高校基本科研業務費(HEUCF160416)；黑龍江省博士后科研啟動基金(LBH-Q15033, LBH-Q14054) 資助課題

U 666.1

A

10.3969/j.issn.1001-506X.2016.09.25

趙琳(1968-),男,教授,博士,主要研究方向為衛星導航、慣性導航。

E-mail:zhaolin@hrbeu.edu.cn

張勝宗(1988-),男,碩士,主要研究方向為衛星導航、精密單點定位。

E-mail:zhangshengzong@hrbeu.edu.cn

網絡優先出版地址：http://www.cnki.net/kcms/detail/11.2422.TN.20160218.1209.004.html