利用格網改正法計算橢球面面積
茹仕高,朱紫陽,區永洪,施一民
(1. 廣東省國土資源測繪院,廣東 廣州 510500; 2. 同濟大學測繪與地理信息學院,上海 200093)
?
利用格網改正法計算橢球面面積
茹仕高1,朱紫陽1,區永洪1,施一民2
(1. 廣東省國土資源測繪院,廣東 廣州 510500; 2. 同濟大學測繪與地理信息學院,上海 200093)
在對高斯投影面積變形定量分析的基礎上,提出了基于高斯投影格網改正的橢球面積計算方法,實現了一次計算、長久受益。該方法直接基于高斯投影面積與已知的格網修正系數,可直接將高斯投影面積轉換為橢球面積,計算簡便、精度高。分別采用一個大圖斑區域和一個小圖斑區域進行了計算驗證,結果表明,該方法能實現相對精度優于1/100萬的計算結果,具有較大的推廣價值。
格網改正;橢球面積;投影變形
面積計算是常見的測量工作,高斯投影面積、橢球面積和地表面積是3類常用統計量[1]。高斯投影面積通常的做法是測量邊界點的坐標,然后計算封閉區域面積,由各頂點的平面直角坐標計算多邊形面積已有簡易可行的熟知公式[2]。隨著地理信息在各領域的廣泛應用,真實地表面與平面差異也需顧及,面積計算由平面轉為橢球面,如第二次全國土地調查、第一次全國地理國情普查要求計算圖斑橢球面積[3-4]。平面面積與橢球面積相比,投影變形不容忽視,王解先[5]等討論了高斯投影中央子午線變化和投影面高程變化引起的面積變形及橢球面面積與高斯面上面積的差異;施鳳翔[6]分析地籍測量中高斯平面上用解析法計算宗地面積的不足,提出了地籍調查宗地面積也應在橢球面上利用封閉區域界址點的大地坐標精確計算宗地面積的方法;呂長廣[7]等分析了土地調查中城鎮和農村分別采用投影平面和橢球面計算面積存在的差異,并提出了采用改算系數法進行平面面積改算。然而,按現有方法用大地經緯線計算橢球面多邊形面積計算量巨大,為提高計算效率,相關科技工作者進行了大量研究以簡化計算量,李玉寶[8]等討論了高斯投影變形引起的面積測算誤差,并分析了變形的量級、性質,提出以高斯平面計算值作為觀測值,運用最小二乘原理、擬合出高斯投影變形拋物線函數,對高斯投影面積計算值進行改正;劉洋[9]等在對高斯投影面積變形的性質及量級進行全面分析的基礎上,顧及地球曲率,提出拋物線擬合面積修正法,用于計算橢球面區域的面積;施一民[10]等推導了基于大地線與測地平行線正交格網的橢球面三角形面積計算公式。上述研究成果對簡化計算量起到了很大的作用,但未就不同拋物線擬合修正適應范圍作出分析;測地型橢球面面積主要適用于測地坐標系,對于大地坐標系需要轉換,轉換計算工作量較大。格網改正法在坐標轉換中現已得到廣泛的應用[11-13],那么可否將其引入用于基于高斯投影平面格網改正的橢球面積計算中呢?本文將探索如何采用這種格網改正法來進行簡便而又精確的橢球面多邊形面積計算。
一、改正原理
1. 高斯投影面積變形
高斯投影為正形投影,根據面積比計算公式可得面積比n與長度比m的關系[14-15]
(1)
式中,Rm為地球平均曲率半徑;y為高斯投影橫坐標。取至二次項為
(2)
由于高斯投影的正形投影的特性,通過計算高斯投影面上的面積比,則直接可以基于高斯投影面積計算橢球面積。由于高斯投影面為一連續面,計算中不可能也無法實現整個面的面積比計算,也無法通過連續面面積比實現橢球面計算,應用中需進行離散化處理,即格網化處理,在計算誤差范圍內以格網中心面積比代替格網內任意處面積比。
2. 格網間距確定
從式(2)可以得出,投影平面上面積變形差異最大的方向為沿橫軸方向,相近等面積圖斑S面積變形差橫軸方向上面積都等于S的兩圖斑的面積變形之差,即
(3)
式中,ym、Δy分別為兩相近圖斑點高斯投影橫坐標均值與差值。為保證計算精度,同名格網內各區域面積變形差應控制在相應的范圍υ限內,即υ≤υ限,由于實際應用中取格網中心處面積變形修正值作為格網內區域變形修正值,同名格網內各區域面積變形最大差可放大1倍,即υ≤2υ限,則
(4)
式中,Δy即為滿足計算精度要求的最大格網尺寸。在南方地區,若取北回歸線(緯度23°26′N)、Rm=6371 km,要求面積變形相對誤差均達到百萬分之一以下,則測區離開中央子午線的距離與格網間距的關系見表1。

表1 測區離開中央子午線的距離與格網間距的關系
實際應用中,大中比例尺測量與調查采用的是3°帶投影,此時測區離開中央子午線的最大距離不超過1.5°,格網間距采用1km即可滿足面積變形相對誤差達到百萬分之一以下。若只需滿足面積變形相對誤差優于10萬分之一,則采用10km的格網間距即可。
3. 格網修正系數計算
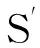
(5)
所對應的橢球面上的面積為
(6)
在南方地區,若取北回歸線(緯度23°26′N)、2000國家大地坐標系橢球、格網間距為1km,則測區離開中央子午線的距離修正系數的關系見表2。
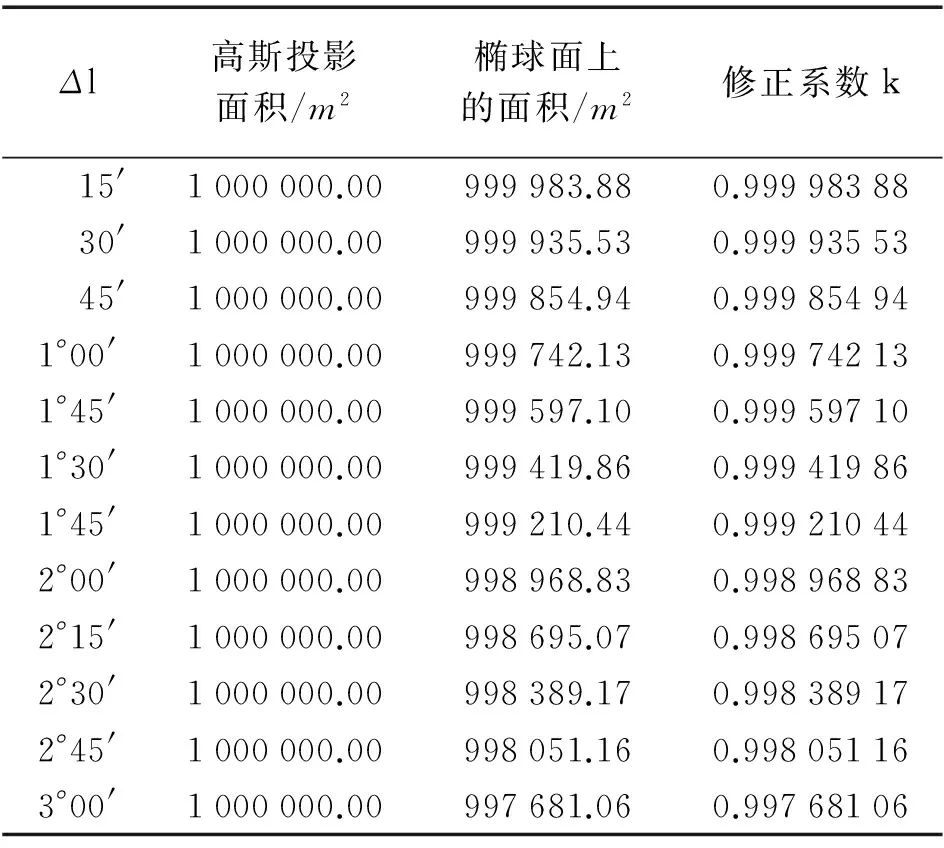
表2 離開中央子午線的距離與修正系數的關系
由表2可知,格網橢球面上的面積小于高斯投影面積,隨著梯形遠離中央子午線面積變形值和面積變形相對誤差逐漸增大,且與式(2)對應的呈拋物線特性,在高斯投影6°帶邊緣地區面積變形相對誤差達到1/430最大。
同時可知,離投影中央子午線越遠,修正系數k值越小。同一格網內,格網中心處修正系數接近真實值;格網中遠離中央子午線計算修正系數k值略大于實際修正系數;格網中近中央子午線計算修正系數k值略小于實際修正系數。因此,格網改正法計算格網內圖斑面積,離中央子午線近的圖斑面積略小于真實圖斑面積,離中央子午線遠的圖斑面積略大于真實圖斑面積。
4. 計算步驟
1) 根據計算精度要求,確定格網間距。
2) 根據格網間距,建立覆蓋計算區域的格網(若用于軟件開發,可計算覆蓋整個中國區域),并計算各格網對應的橢球面上的面積及修正系數。
3) 對圖斑與格網進行空間分析,計算圖斑對應的格網。
4) 需計算橢球面積多邊形的高斯投影面積。
5) 進行計算多邊形的面積變形修正,獲取各多邊形對應的橢球面上的面積。
二、實例分析
1. 算例1
為說明該方法的通用性,選擇了如圖1所示南方某一縣級行政區的遙感調查成果進行圖斑橢球面上的面積計算。計算區域總面積約2365km2,離中央子午線最小、最大距離分別為43′、1°25′,共有圖斑109 865個,圖斑最小上圖圖斑面積200m2,最大圖斑面積235.3km2,平均圖斑面積20 712.9m2。按照1km間距建立CGCS2000高斯投影格網,采用10m間距加密格網邊界,采用真實橢球面上的面積計算公式分別計算各格網橢球面上的面積及修正系數。

圖1 試驗區域及圖斑邊界
為比較計算精度,采用真實橢球面上的面積計算公式計算了各圖斑的真實橢球面上的面積,另采用本文介紹的格網改正法計算了各圖斑橢球面上的面積,兩者比較的統計結果見表3。
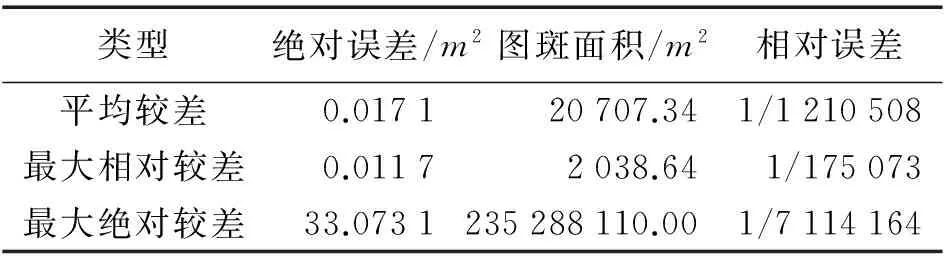
表3 圖斑格網改正法計算誤差統計
計算結果表明,以格網改正法計算的109 865個圖斑的橢球面上的面積與理論面積相比較,面積較差絕對值均值為0.017 1m2、相對誤差為1/1 210 508,即平均面積變形相對誤差在百萬分之一以下;最大較差絕對值為33.07m2,其對應相對誤差為1/7 114 164,優于700萬分之一;最大相對較差為1/175 073,其對應較差絕對值為0.011 7m2,優于10萬分之一。
計算結果同時表明,相對精度優于百萬分之一的圖斑為40 715個,占37.1%,未達到設定的要求百萬分之一。究其原因主要是真實橢球面上的面積與改正計算橢球面上的面積差異很小(較差小于1m2的為109 673個圖斑,占99.8%;較差大于10m2的圖斑數僅為15個),0.000 1m2的計算誤差將產生原本優于百萬分之一的相對誤差而變為相對誤差僅優于10萬分之一,而實際絕對較差很小,對面積計算產生的影響完全可以忽略。故整體改正計算效果應是顯著的。
2. 算例2
為說明該方法的通用性,選擇了廣東陸域行政區各縣級行政區進行橢球面上的面積計算。計算區域總面積約17.96萬km2,選擇114°作為高斯投影中央子午線,計算區域離開中央子午線最大距離為4°21′,共有多邊形123個,最大多邊形面積5634km2,平均多邊形面積1 463.13km2。按照10km間距建立CGCS2000高斯投影格網,采用10m間距加密格網邊界,采用真實橢球面上的面積計算公式分別計算各格網橢球面上的面積及修正系數。
為比較計算精度,采用真實橢球面上的面積計算公式計算了各圖斑的真實橢球面上的面積,并采用本文介紹的格網改正法計算了各圖斑橢球面上的面積,得到各圖斑的兩種面積結果其統計見表4。
表4用格網改正法計算各縣級行政區橢球面上的面積的誤差統計
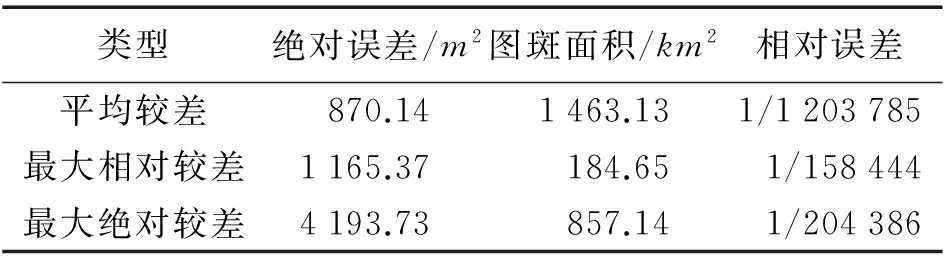
類型絕對誤差/m2圖斑面積/km2相對誤差平均較差870.141463.131/1203785最大相對較差1165.37184.651/158444最大絕對較差4193.73857.141/204386
計算結果表明,以格網改正法計算的123個縣級行政區的橢球面上的面積與理論面積相比較,面積較差絕對值均值為870.14m2、相對誤差1/1 203 785,即平均面積變形相對誤差在百萬分之一以下;最大較差絕對值為4 193.73m2,其對應相對誤差為1/204 386,優于20萬分之一;最大相對較差為1/158 444,其對應較差絕對值為1 165.37m2,優于10萬分之一。如此大區域計算,都能滿足計算精度要求。
計算結果同時表明,相對精度優于百萬分之一的圖斑為96個,占78.0%;相對精度優于50萬分之一的圖斑為112個,占91.1%。遠優于按照預定的格網間距相對精度應優于10萬分之一的要求,究其原因主要有兩個方面:①格網間距達到了對相對精度的最低要求;②各圖斑跨越格網,格網改正法修正面積與實際橢球面上的面積有正有負,存在計算誤差相互抵消的現象。
三、結束語
本文結合地理空間信息應用中大量橢球面上的面積計算的需要,對高斯投影面積變形進行了分析,在此基礎上,顧及橢球面上的面積計算的復雜性、高斯投影面積計算的簡單性,提出了基于高斯投影格網改正的橢球面上的面積計算方法。該方法直接基于高斯投影面積及已知的格網修正系數,可直接將高斯投影面積轉換為橢球面上的面積,計算簡便、精度高。
分別采用了一個2000多平方千米的縣級行政區遙感調查涉及109 865個圖斑、廣東省所有縣級行政區陸域(含南澳縣)123個圖斑,分別采用真實橢球面上的面積計算公式與格網改正法計算了相應圖斑橢球面上的面積。結果表明,計算結果能實現總體百萬分之一的計算精度,能滿足應用上的各項需求,該方法具有較大的推廣價值。
[1]薛樹強,黨亞民,秘金鐘,等. 顧及非線性地形因子的地表面積計算[J]. 測繪學報,2015,44(3):330-337.
[2]顧孝烈,鮑峰,程效軍. 測量學[M]. 4版.上海:同濟大學出版社,2011.
[3]中華人民共和國國土資源部.第二次全國土地調查技術規程:TD/T1014—2007[S].北京:[s.n.],2007.
[4]第一次全國地理國情普查領導小組辦公室.地理國情普查基本統計分析技術規定:GDPJ02—2013[S].北京:[s.n.],2013.
[5]王解先,俞振武. 高斯投影引起的面積誤差[J]. 測繪通報,2003(4):5-6.
[6]施鳳翔. 基于橢球面的城鎮地籍宗地面積量算方法研究[C]∥地理信息與物聯網論壇暨江蘇省測繪學會2010年學術年會論文集. 無錫:江蘇省測繪學會,2010.
[7]呂長廣,張先為,李淑青. 土地調查中城鄉土地面積計算的差別及其處理方法[J]. 地礦測繪,2008,24(3):9-11.
[8]李玉寶,曹智翔. 顧及地球曲率的面積計算問題[J]. 重慶交通學院學報,2007,26(1):152-154.
[9]劉洋,高井祥,王堅,等. 基于拋物線擬合的橢球面區域面積計算方法[J]. 大地測量與地球動力學, 2015, 35(2): 228-231.
[10]施一民,朱紫陽. 測地坐標計算橢球面上凸多邊形面積的算法[J]. 同濟大學學報(自然科學版),2006,34(4):504-507.
[11]郭充,呂志平,李巖,等. 基于格網的坐標轉換方法[J]. 信息工程大學學報,2010,11(2):166-169.
[12]呂志平,魏子卿,李軍,等.CGCS2000高精度坐標轉換格網模型的建立[J]. 測繪學報,2013,42(6):791-797.
[13]劉文建,施闖. 基于格網改正的CORS實時三維坐標服務系統[J]. 測繪通報,2013(10):70-72.
[14]施一民. 現代大地控制測量[M]. 2版.北京:測繪出版社,2007.
[15]孔祥元,郭際明,劉宗泉. 大地測量學基礎[M]. 2版.武漢:武漢大學出版社,2010.
Study on Ellipsoid Surface Area Calculation Method Using Grid Correction Technology
RU Shigao,ZHU Ziyang,OU Yonghong,SHI Yimin
10.13474/j.cnki.11-2246.2016.0274.
2015-10-08;
2016-03-07
國家科技支撐計劃(2012BAB16B01);國家自然科學基金(40471114)
茹仕高(1965—),男,高級工程師,主要研究方向為大地測量和工程測量。E-mail:332575991@qq.com
P226
B
0494-0911(2016)08-0124-04
引文格式:茹仕高,朱紫陽,區永洪,等.利用格網改正法計算橢球面面積[J].測繪通報,2016(8):124-127.

