基于無監督判別投影的滾動軸承故障診斷

江　麗　郭順生

武漢理工大學,武漢,430070

?

基于無監督判別投影的滾動軸承故障診斷

江麗郭順生

武漢理工大學,武漢,430070

針對滾動軸承故障樣本不平衡和故障特征存在冗余性問題，提出了基于無監督判別投影(UDP)的滾動軸承故障診斷方法。該方法首先從時域和時頻域提取多個特征參數，從而構造一個原始的高維特征集，隨后運用UDP算法從該特征集中提取最敏感的低維流形特征，最后利用K-近鄰分類器識別出滾動軸承的運行狀態。將該方法分別應用于軸承故障類型和內圈故障嚴重性的識別，并與傳統方法進行了比較，驗證了該方法的可行性和優越性。

故障診斷；特征提取；流形學習；無監督判別投影

0　引言

滾動軸承是現代工業設備中應用最廣泛也最易失效的零件之一，其運行狀態將直接影響到整臺設備的可靠性、使用壽命和安全性。因此，滾動軸承的故障診斷對保障設備可靠運行、延長其使用壽命和避免重大事故具有重要意義[1-4]。為了全面獲取滾動軸承的故障信息，常從多個角度提取較多的特征參數，但這會導致特征維數過高。另外，特征參數之間可能存在冗余性或不相關性，往往會降低后續分類器的診斷精度，因此，必須采用維數約簡的方法，提取有利于軸承故障分類的低維融合特征[5-7]。

傳統的維數約簡方法，如主成分分析(principalcomponentanalysis，PCA)算法[8]和線性判別分析(lineardiscriminantanalysis，LDA)算法[9]，主要用于處理歐氏空間中具有全局線性結構的高維故障數據。然而，大多數機械零件的失效都伴隨著非線性行為[10]。流形學習算法由于能充分挖掘非線性數據中的潛在幾何結構和內在規律，近年來它在機械故障診斷中的應用研究備受國內外研究者的關注[1-7,11-12]。經典的流形學習算法無法獲取從高維空間到低維空間的映射函數，因此He等[13]提出了局部保持投影(localitypreservingprojections，LPP)算法。雖然LPP算法能很好地解決樣本外點問題，但是它與大多數流形學習算法一樣，都是基于保持局部幾何結構進行流形建模，這與分類目標并無直接關系。無監督判別投影(unsuperviseddiscriminantprojection，UDP)[14]算法是一種新型的流形學習算法，它不僅具有較強的泛化能力，而且通過最小化局部散度同時最大化非局部散度來建立目標函數，從而挖掘潛藏在高維數據中的低維流形，因而其提取的低維特征具有更強的分類能力。

機械設備的故障診斷實質上是多個故障模式的識別問題。由于機械設備大多處于正常的運行工況，因此滾動軸承多類故障樣本的積累往往是一個極其緩慢的過程，其獲取過程比較費時費力。隨著傳感器技術的飛速發展，獲取大量正常狀態的樣本非常容易。由此，產生了樣本不平衡問題。為了解決滾動軸承多個故障模式的識別、故障特征存在冗余性和樣本不平衡等問題，本文首次提出了基于無監督判別投影的滾動軸承故障診斷方法。該方法首先提取滾動軸承的多個特征參數，從而構造一個原始的高維特征集；然后通過UDP算法挖掘嵌入在高維特征集中的低維流形結構，并提取最敏感的低維流形特征；最后利用K-近鄰(K-nearestneighbor，KNN)分類器實現滾動軸承故障類型和內圈故障嚴重性的識別。

1　無監督判別投影

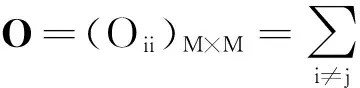
(1)

其中，SL為局部散度矩陣，其定義為

(2)

在低維嵌入空間Rd中非局部散度JN(w)定義為

wT(ST-SL)w

(3)

其中，ST稱為總體散度矩陣，即數據集的協方差。定義非局部散度矩陣SN=ST-SL。

為了保證高維空間中，兩個近距離的樣本投影到低維空間后離得更近，兩個遠距離的樣本投影到低維空間后離得更遠，必須最大化非局部散度，同時最小化局部散度。因此，UDP算法的最終優化目標函數為

(4)

通過矩陣變換理論，式(4)可以轉化為廣義特征方程SNw=λSLw的最大特征值分解問題。其中，λ為特征值。因此，UDP算法的最佳投影方向為其d 個最大特征值所對應的特征向量。

對于一個新樣本點xnew，它的低維嵌入ynew為

ynew=(w*)Txnew

(5)

2　基于無監督判別投影的軸承故障診斷模型

本文根據滾動軸承的故障特點，在UDP算法基礎上，提出了基于多域特征構建、維數約簡和特征融合、模式分類的診斷模型，如圖1所示。其基本思想是：從故障信號中提取多個特征參數構造高維特征集，利用UDP算法對高維特征集進行流形學習，提取能有效挖掘故障數據本質結構的低維敏感特征來表征軸承的運行狀態，并將所有低維流形特征輸入分類器進行模式分類，找出故障原因。該模型的故障診斷過程如下。

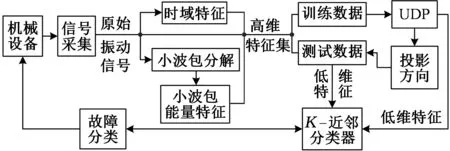
圖1　基于UDP算法的故障診斷模型

2.1構造高維特征集

為了更全面地獲取滾動軸承的故障信息，將綜合利用時域統計特征參數和小波包能量特征參數來描述滾動軸承的運行狀態。從監測設備采集振動信號后，提取原始振動信號的11個時域統計特征(均值、標準方差、均方根值、方根幅值、峰-峰值、偏度、峭度、峰值因子、裕度因子、波形因子、沖擊因子)；采用db2小波包對原始振動信號進行4層正交小波包分解后，得到16個子頻帶的小波包重構信號，將16個子頻帶的小波包能量和第4層所有頻段的小波包總能量的比值作為小波包能量特征參數。因此，共得到具有27個特征參數的原始高維特征集來表征軸承的運行狀態，其詳細的計算公式和定義見文獻[15]。

她不穿襪子，任憑俊氣的、涂了紅色指甲油的腳指頭從兩只白涼鞋的露孔中鉆出來，更加惹人注意。這很像咖啡館里的光線，是種撩撥人的暗色的場景。使人聯想到某個深夜里的某一種夢境，伴著咖啡館里細碎的音樂，肆意的彌漫和張揚。

2.2提取低維流形特征

盡管上述27個特征參數可以較全面地描述軸承的運行狀態，然而它們之間可能存在冗余性或不相關性，這往往會降低后續分類器的診斷性能。因此，利用UDP算法進行維數約簡和特征融合，從原始高維特征集中，提取有利于故障分類的低維敏感特征，并剔除原始高維特征集中的冗余或不相關信息。首先，將27維特征集分成兩部分，一部分用作訓練數據，一部分用作測試數據。然后，利用UDP算法對27維特征集中的訓練數據進行流形學習，挖掘27維訓練樣本中的潛在故障信息，從而得到其低維流形特征和最佳投影方向。最后，根據最佳投影方向可得到27維測試樣本的低維流形特征。

2.3故障模式分類

將訓練樣本和測試樣本的 d 維流形特征輸入KNN分類器，根據訓練樣本的類別信息，對測試樣本進行故障模式分類，從而診斷出滾動軸承的故障類型或者內圈故障損傷程度。

由于UDP算法通過構建局部近鄰圖來挖掘潛藏在高維數據中的低維流形，因此近鄰點數k的選取將影響低維流形特征的提取，繼而影響后續分類器的診斷性能。根據文獻[14]的研究結果，本文最優的近鄰點數k為每類訓練樣本數減一，并根據最高的故障識別精度來選取最優的嵌入維數d。

3　故障診斷實驗

本文實驗數據來源于美國凱斯西儲大學(CaseWesternReserveUniversity)電氣工程實驗室的滾動軸承故障模擬實驗臺[16]。如圖2所示，實驗臺由1491.4W三相電動機、扭矩傳感器和加載電機組成，待測試的滾動軸承(型號為6205-2RSJEMSKF)安裝在電動機驅動端，加速度傳感器粘貼于電動機驅動端正上方的機殼上。當電機轉速為1772r/min、工作載荷為745.7W時，四種直徑的單點故障通過放電加工引入到滾動軸承，所有故障深度均為0.28mm。故障軸承的振動數據由一個16通道的數據記錄儀獲取，采樣頻率為12kHz，數據樣本長度為1024。

圖2　滾動軸承故障模擬實驗臺

為了驗證本文方法的有效性和優越性，進行了滾動軸承故障類型和內圈故障損傷程度的識別，并與經典的模式識別方法，如PCA+KNN算法、LDA+KNN算法以及LPP+KNN算法進行了比較，具體如下：分別采用PCA算法、LDA算法或者LPP算法，從原始高維特征集中提取低維故障特征后，再采用K-近鄰分類器進行故障模式分類。

3.1滾動軸承故障類型的識別

當滾動軸承的單點損傷直徑為0.18mm時，模擬了滾動軸承的 4 種故障狀態：①內圈故障；②滾動體故障；③外圈故障；④正常運行狀態。 前三種故障狀態各采集50個樣本，正常運行狀態采集90個樣本。每類選取后20個樣本為測試樣本，其余為訓練樣本。根據第2節的方法，確定UDP算法的近鄰點個數k=29。

當采用四種特征提取算法來識別滾動軸承四種故障類型時，其對應的最高分類精度見表1。從表1中可以看出，LDA算法的最高故障分類精度(滾動體故障為55%，正常狀態為55%)明顯低于基于UDP算法的故障診斷方法(對應分類精度均為100%)。與PCA算法相比較，UDP算法對應的滾動體故障和正常狀態的最高故障識別率分別提高了25%和5%。可見，LDA算法和PCA算法的基于全局結構的數據挖掘特性不利于故障分類，因而它們只能完全區分內圈故障和外圈故障。盡管LPP算法能保持故障數據的局部幾何結構，而且可以完全區分三類故障狀態，但滾動體故障的最高分類精度只有75%。這是因為UDP算法通過最小化局部散度同時最大化非局部散度來挖掘潛藏在故障數據中的低維流形，從而剔除原始高維特征集中的冗余或不相關信息，保留能表征軸承運行狀態的低維敏感特征，因而它比只考慮局部散度的LPP算法具有更好的分類性能。另外，基于UDP算法的故障診斷方法以相對較低的特征維數取得了最好的故障識別效果。因此，與PCA算法、LDA算法和LPP算法相比較，UDP算法能明顯提高不平衡樣本情況下軸承四種故障類型的識別精度。

表1不同特征提取算法對應的最高故障分類精度

%

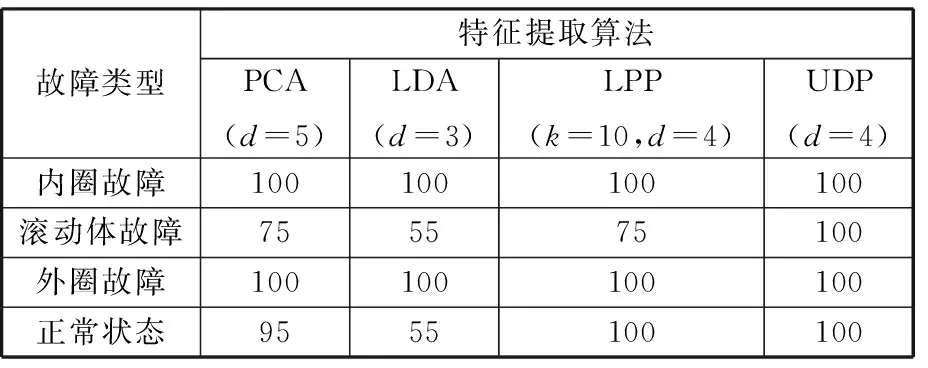
為了檢驗UDP算法的噪聲魯棒性，將隨機噪聲添加到滾動軸承的四類測試樣本中。圖3所示為不同噪聲百分比條件下，上述四種特征提取算法的故障識別結果。由圖3可知，當噪聲百分比不超過30%時，除了LDA算法外，另外三種特征提取算法都能取得比較滿意的故障識別效果。而且，在相同噪聲百分比條件下，UDP算法的故障識別性能均要優于另外三種特征提取算法，特別是當噪聲百分比為50%時，UDP算法的故障識別精度高于85%，而另外三種特征提取算法均低于80%。因此，與PCA算法、LDA算法和LPP算法相比較，基于UDP算法的故障診斷模型具有最優的故障識別性能及抗噪性能。

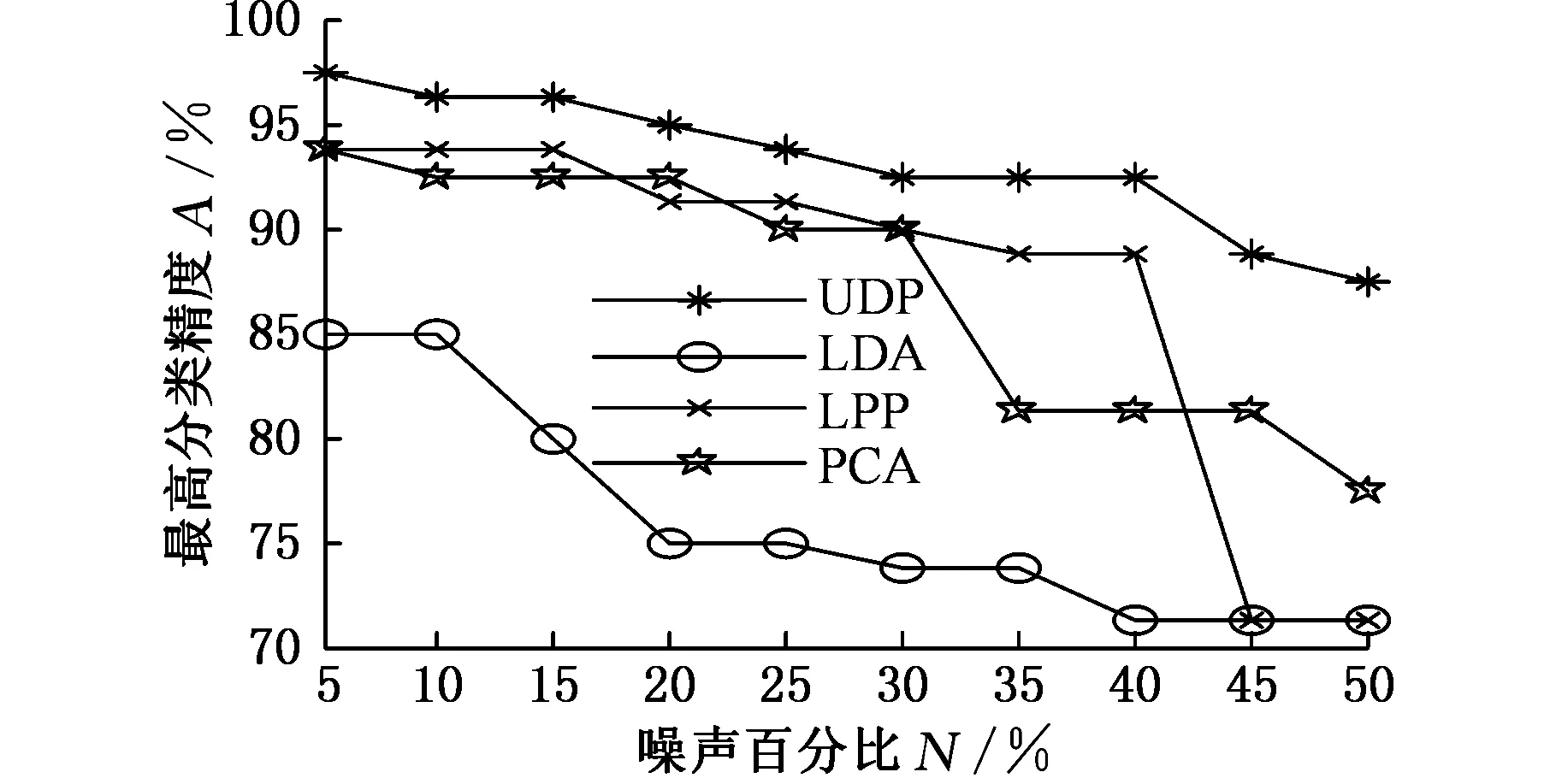
圖3　不同噪聲百分比下軸承故障類型的識別精度

3.2內圈故障嚴重性的識別

模擬了滾動軸承內圈的 5種損傷狀態：①輕度內圈故障(單點損傷直徑為0.18 mm)；②中度內圈故障(單點損傷直徑為0.36 mm)；③重度內圈故障(單點損傷直徑為0.54 mm)；④非常重度內圈故障(單點損傷直徑為0.72 mm)；⑤正常運行狀態。前四種故障狀態各采集50個樣本，正常運行狀態采集90個樣本。每類選取后20個樣本為測試樣本，其余為訓練樣本。根據第2節的方法，確定UDP算法的近鄰點個數k=29。

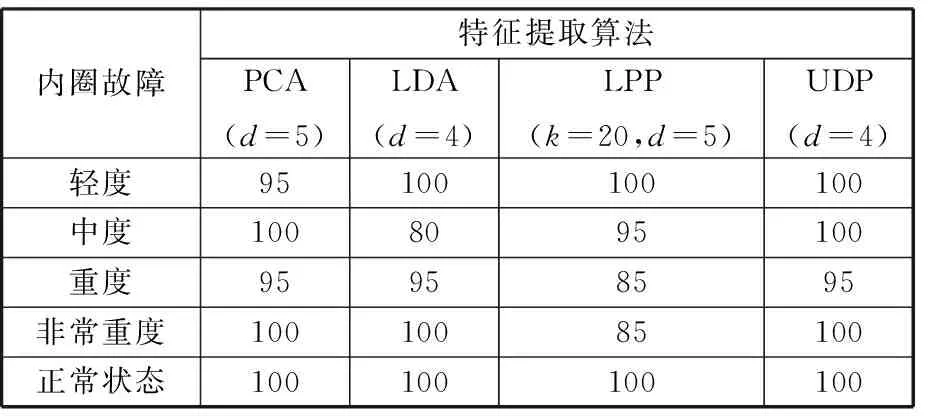
當采用四種特征提取算法來識別滾動軸承內圈五種損傷狀態時，其對應的最高分類精度見表2。由表2可以看出，與另外三種特征提取算法相比較，LPP算法具有最差的故障分類性能，它只能完全區分軸承內圈的三種損傷狀態，其最高故障分類精度(中度內圈故障為95%、重度內圈故障為85%、非常重度內圈故障為85%)低于基于UDP算法的故障診斷方法(對應值分別為100%、95%和100%)，這是因為LPP算法只能保證屬于同一個聚類的故障樣本投影到低維空間后離得更近，但是無法保證不同聚類的故障樣本投影到低維空間后離得更遠。與LDA算法相比較，UDP算法對應的中度內圈故障的分類精度提高了20%；與PCA算法相比，UDP算法對應的輕度內圈故障的分類精度提高了5%。因此，相對于另外三種特征提取算法而言， UDP算法能明顯提高不平衡樣本情況下軸承內圈故障嚴重性的識別精度。

表2不同特征提取算法對應的最高故障分類精度

%

將隨機噪聲添加到軸承內圈的五類測試樣本中，圖4所示為不同噪聲百分比條件下，上述四種特征提取算法的故障識別結果。由圖4可知，在相同噪聲百分比條件下，UDP算法的故障識別性能均要優于另外三種特征提取算法。而且，當噪聲百分比從5%增大到50%時，UDP算法的故障識別率的波動幅度最小。因此，與PCA算法、LDA算法和LPP算法相比較，基于UDP算法的故障診斷模型具有更好的噪聲魯棒性。

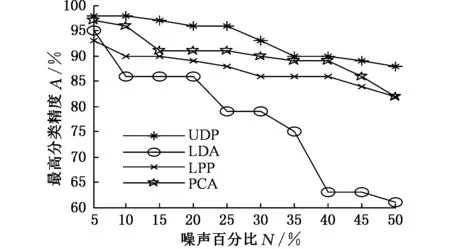
圖4　不同噪聲百分比下內圈損傷程度的識別精度

4　結論

本文提出一種基于UDP算法的滾動軸承故障診斷方法，該方法從故障信號中提取11個時域統計特征和16個小波包能量特征后，利用UDP算法挖掘高維特征集中的潛在流形結構，從而提取低維敏感特征來表征軸承的運行狀態。將該方法應用于滾動軸承四種故障類型和內圈五種損傷程度的識別，實驗結果表明，相對于LDA算法、LPP算法和PCA算法，UDP算法能明顯提高不平衡樣本情況下軸承的故障識別精度，其提取的低維流形特征具有更優的故障識別性能和噪聲魯棒性。

[1]劉麗娟, 陳果, 郝騰飛. 基于流形學習與一類支持向量機的滾動軸承早期故障識別方法[J]. 中國機械工程，2013，24(5): 628-633.

LiuLijuan,ChenGuo,HaoTengfei.IncipientFaultRecognitionofRollingBearingsBasedonManifoldLearningandOne-classSVM[J].ChinaMechanicalEngineering, 2013，24(5): 628-633.

[2]歐璐, 于德介. 基于拉普拉斯分值和模糊C均值聚類的滾動軸承故障診斷[J]. 中國機械工程，2014，25(10): 1352-1357.

OuLu,YuDejie.RollingBearingFaultDiagnosisBasedonLaplacianScoreandFuzzyC-meansClustering[J].ChinaMechanicalEngineering, 2014，25(10): 1352-1357.

[3]WangYi,XuGuanghua,LiangLin,etal.DetectionofWeakTransientSignalsBasedonWaveletPacketTransformandManifoldLearningforRollingElementBearingFaultDiagnosis[J].MechanicalSystemsandSignalProcessing, 2015, 54: 259-276.

[4]DingXiaoxi,HeQingbo,LuoNianwu.AFusionFeatureandItsImprovementBasedonLocalityPreservingProjectionsforRollingElementBearingFaultClassification[J].JournalofSoundandVibration, 2015, 335: 367-383.

[5]YuJianbo.BearingPerformanceDegradationAssessmentUsingLocalityPreservingProjections[J].ExpertSystemswithApplications, 2011, 38(6): 7440-7450.

[6]HuangYixiang,ZhaXF,LeeJ,etal.DiscriminantDiffusionMapsAnalysis:aRobustManifoldLearnerforDimensionalityReductionandItsApplicationsinMachineConditionMonitoringandFaultDiagnosis[J].MechanicalSystemsandSignalProcessing, 2013, 34(1): 277-297.

[7]黃宏臣, 韓振南, 張倩倩，等. 基于拉普拉斯特征映射的滾動軸承故障識別[J]. 振動與沖擊，2015，34(5): 128-134.

HuangHongchen,HanZhennan,ZhangQianqian,etal.MethodofFaultDiagnosisforRollingBearingsBasedonLaplacianEigenmap[J].JournalofVibrationandShock, 2015，34(5): 128-134.

[8]JolliffeIT.PrincipalComponentAnalysis[M].NewYork:Springer, 1986.

[9]BelhumeurPN,HespanhaJP,KriegmanDJ.EigenfacesVs.Fisherfaces:RecognitionUsingClassSpecificLinearProjection[J].IEEETransactionsonPatternAnalysisandMachineIntelligence, 1997, 19(7): 711-720.

[10]HeQingbo.Time-frequencyManifoldforNonlinearFeatureExtractioninMachineryFaultDiagnosis[J].MechanicalSystemsandSignalProcessing，2013, 35(1/2):200-218.

[11]蘇祖強, 湯寶平, 劉自然，等. 基于正交半監督局部fisher判別分析的故障診斷[J]. 機械工程學報，2014，50(18): 7-13.

SuZuqiang,TangBaoping,LiuZiran,etal.FaultDiagnosisMethodBasedonOrthogonalSemi-supervisedLocalFisherDiscriminantAnalysis[J].JournalofMechanicalEngineering, 2014，50(18): 7-13.

[12]孫斌, 劉立遠, 牛翀，等. 基于局部切空間排列和K-最近鄰分類器的轉子故障診斷方法[J]. 中國機械工程，2015，26(1): 74-78.

SunBin,LiuLiyuan,NiuChong,etal.RotorFaultDiagnosisMethodsBasedonLocalTangentSpaceAlignmentandK-NearestNeighborClassifier[J].ChinaMechanicalEngineering, 2015，26(1): 74-78.

[13]HeXiaofei,NiyogiP.LocalityPreservingProjections[C]//Proceedingofthe17thAnnualConferenceonNeuralInformationProcessingSystems.Cambridge:MITPress, 2003: 153-160.

[14]YangJian,ZhangDavid,YangJingyu,etal.GloballyMaximizing,LocallyMinimizing:UnsupervisedDiscriminantProjectionwithApplicationstoFaceandPalmBiometrics[J].IEEETransactionsonPatternAnalysis&MachineIntelligence, 2007, 29(4): 650-664.

[15]JiangLi,ShiTielin,XuanJiangping.FaultDiagnosisofRollingBearingsBasedonMarginalFisherAnalysis[J].JournalofVibrationandControl, 2014, 20(3): 470-480.

[16]LoparoKA.BearingsVibrationDataSet[DB/OL][2014-10-28].http: //Csegroups.Case.Edu/Bearingdatacenter/Home.

(編輯盧湘帆)

FaultDiagnosisofRollingBearingsBasedonUnsupervisedDiscriminantProjection

JiangLiGuoShunsheng

WuhanUniversityofTechnology,Wuhan,430070

Aimingattheimbalancedfaultsamplesandredundantfaultfeaturesofrollingbearings,arollingbearingfaultdiagnosismethodwasproposedbasedonUDP.Themethodfirstlyextractedseveralfeatureparametersfromtimedomainandtime-frequencydomain.Thus,therawhigh-dimensionalfeaturesetwasconstructed.Subsequently,themostsensitivelow-dimensionalmanifoldfeatureswereextractedfromthefeaturesetbyemployingUDPalgorithm.Finally, K-nearestneighborclassifierwasutilizedtorecognizetheoperatingconditionsofrollingbearings.Themethodwasappliedtotheidentificationofbearingfaultcategoriesandinnerfaultseveritiesseparately.Comparedwiththetraditionalmethods,thefeasibilityandsuperioritywerevalidated.

faultdiagnosis；featureextraction；manifoldlearning；unsuperviseddiscriminantprojection(UDP)

2016-03-29

國家自然科學基金資助項目(71171154);湖北省自然科學基金資助項目(2015CFB698);湖北省科技支撐計劃資助項目(2014BAA032，2015BAA063)

TP206；TP391.4

10.3969/j.issn.1004-132X.2016.16.013

江麗，女，1980 年生。武漢理工大學機電工程學院助理研究員。主要研究方向為機械設備狀態監測與故障診斷、模式識別。發表論文3篇。郭順生(通信作者)，男，1963 年生。武漢理工大學機電工程學院教授、博士研究生導師。