排水口旋渦的壓強與速度分布

方愛平　田蓬勃　孫迪昊　牛斯雋　朱明輝　魏明華　喻有理　王小力（西安交通大學理學院，陜西西安 710049）

物理與工程

排水口旋渦的壓強與速度分布

方愛平田蓬勃孫迪昊牛斯雋朱明輝魏明華喻有理王小力
（西安交通大學理學院，陜西西安 710049）

本文對自由表面液體在重力作用下形成排水旋渦的性質(zhì)進行了研究，分析了當旋渦達到穩(wěn)定狀態(tài)時內(nèi)部速度與壓強的分布，并由此確定了旋渦產(chǎn)生的凹陷液體上表面形狀.本文用類似蘭金渦模型的思想，以一臨界半徑為界線，半徑以外采用自由旋渦模型，在靠近渦心處使用等角速度模型以避免奇點的出現(xiàn).這一模型可以給出旋渦內(nèi)部的壓強和速度分布規(guī)律，能定性解釋不同粘度流體形成旋渦形狀的差異.

自由旋渦；蘭金渦；點匯；點渦

生活中，當一些容器由下方排水孔排水時，在一定條件下，排水孔上方會出現(xiàn)水流的旋轉(zhuǎn)運動，轉(zhuǎn)動較劇烈時，液面會下凹，形成一個旋渦.這種排水渦旋的具體形成機制較為復雜，其具體原因不在本文討論范圍之內(nèi).本文主要探究旋渦進入穩(wěn)定狀態(tài)（排水中期，旋渦隨時間幾乎不發(fā)生形態(tài)變化）時，液體內(nèi)部的壓強、速度分布及液體表面形態(tài).

1　自由旋渦模型

自由旋渦模型在計算中不考慮粘滯阻力的影響，僅從流體的動力學出發(fā)，在一定范圍下可以對旋渦進行描述.

1.1二維的自由旋渦流動

相比于三維流動，二維平面上的速度分布更容易求解，現(xiàn)考慮二維平面上的排水旋渦，在極坐標極點設一排水口，液體一邊繞極點旋轉(zhuǎn)流動，一邊匯入極點.

對于較為復雜的二維平面勢流，可以表示為一些簡單平面勢流的線性疊加.一般情況下，認為平面的自由匯聚旋渦可以看作是點匯平面勢流（如圖1所示）和點渦平面勢流（如圖2所示）的疊加［1］.

點匯勢流中，液體流線均指向極點，等速度面為同心圓，液體沿徑向流入極點排水口，無旋轉(zhuǎn)運動.由于流體的不可壓縮性，假設單位時間由極點排出的流量為Q［1］，其基本屬性可描述為

速度勢函數(shù)：

流函數(shù)：

速度分布：

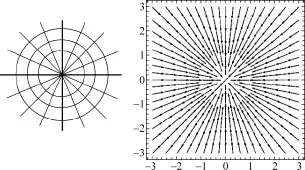
圖1 點匯勢流（左）和點匯速度場分布圖（右）

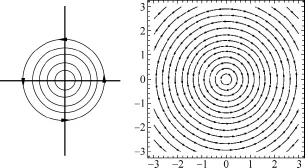
圖2 點渦勢流（左）和點渦速度場分布圖（右）

點渦勢流中，液體不作徑向方向的流動，流線為圓心位于極點的同心圓族.根據(jù)亥姆霍茲定理，其每一條流線的速度環(huán)量（點渦強度）為一定值，設為Γ（這里忽略了粘性作用）［1］.其基本屬性可描述為

速度勢函數(shù)：

流函數(shù)：

速度分布：

將點匯與點渦的速度分布進行疊加，就可以得到二維平面排水旋渦的速度場分布

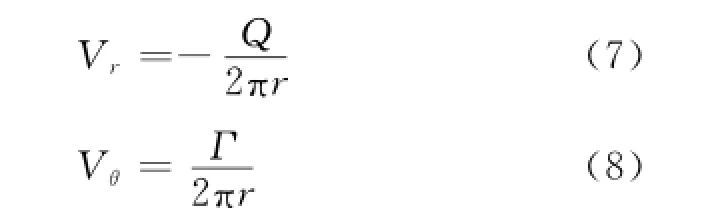
其分布圖如圖3所示.

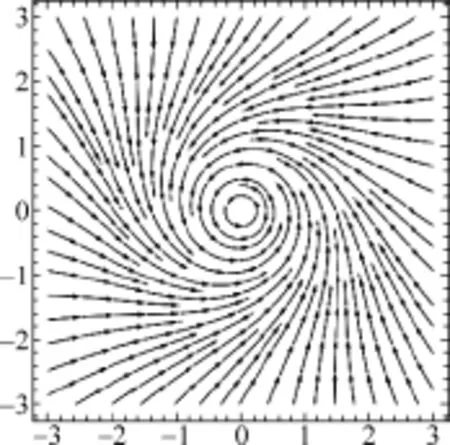
圖3 二維排水旋渦速度場分布

1.2 三維的自由旋渦流動

對于三維的流動情況，液體將一邊在水平面內(nèi)作渦旋流動，一邊受重力向下運動至出水口流出（如圖4左圖所示）.若在某一半徑處取一個環(huán)形柱面，則該柱面上的流量等于排水孔流量，并且重力的作用只對豎直方向的速度產(chǎn)生影響，因而認為流體內(nèi)部的水平面的速度分布與二維流動的情形一致，即

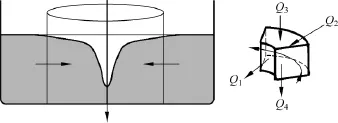
圖4 三維旋渦（左）和三維旋渦微元（右）

由上述結(jié)論，我們可以得出一個推論，在流體中取一小微元（如圖4右圖所示），其徑向方向流入量等于流出量，即Q1=Q2，由于Vθ與θ無關(guān)，故與轉(zhuǎn)動方向正交的兩個平面的流入量之和為零，即Q3=Q4，由此可以推出

則三維流動的速度分布滿足

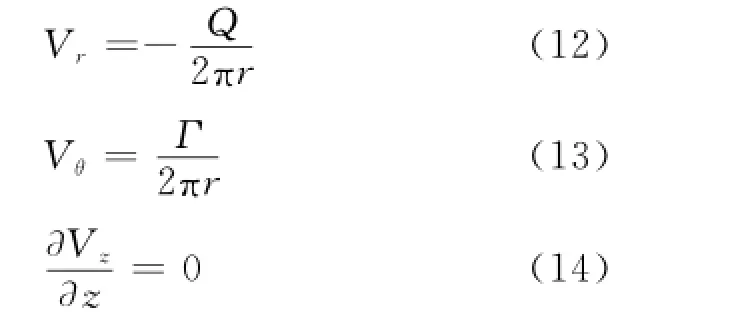
根據(jù)方程（12）～（14），可以繪制出速度場圖像（如圖5所示）.

圖5　三維旋渦速度場分布

1.3三維自由旋渦內(nèi)的壓強分布

不考慮粘滯阻力的情況下，流體內(nèi)部的壓強是空間位置的函數(shù)，在柱坐標系下可寫為p= p（r，θ，z），其微分表達式為

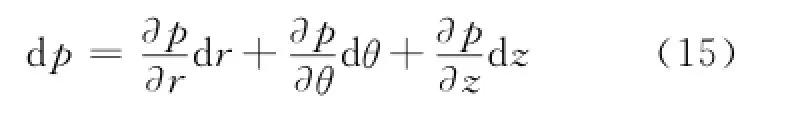
在相對靜止流體中，單位質(zhì)量流體所受的重力、慣性力與壓力相平衡［1］，即

其中，g為重力加速度，a為慣性加速度，p為流體密度.在柱坐標系下各分量表達為

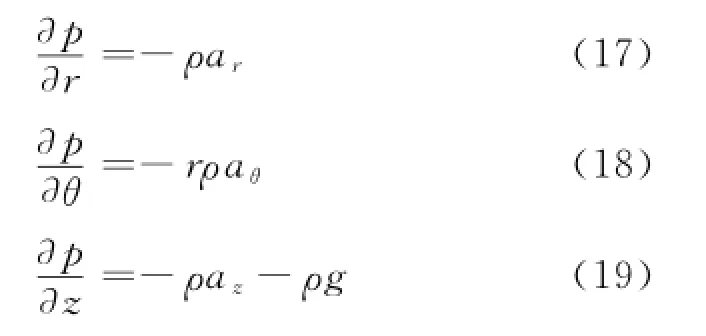
根據(jù)之前求得的速度場分布式（12）～式（14），可以計算出各點的加速度表達式

將式（20）～式（22）代入式（17）～式（19），可得壓強各分量的偏導數(shù)

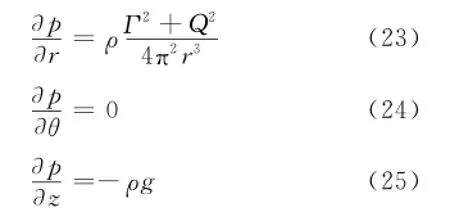
積分可得

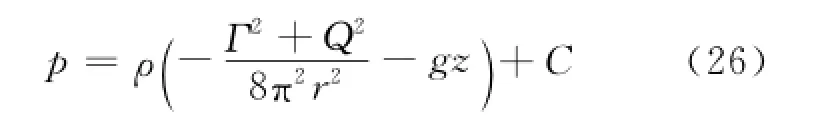
其中，C為待定常數(shù)，設原流體平面為z軸零點，則當r→∞時，p→p0（p0為液體表面大氣壓），從而可以確定C=p0，壓強表達式為

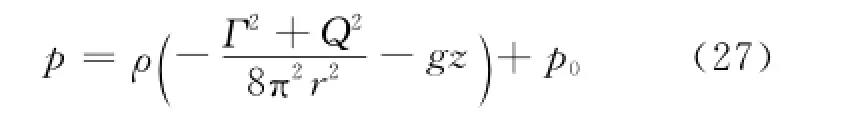
該公式即描述了液體內(nèi)部的壓強分布情況.

1.4三維自由旋渦的上表面形態(tài)

根據(jù)壓強分布式（26），可以繪制等壓強面.而液體上表面即為p=p0的等壓面，代入壓強分布表達式（26），可得等壓強曲面方程為

荔枝 性溫、味甘、酸，具有補脾益肝、生津止渴、解毒止瀉等功效。荔枝可改善人的肝腎功能，加速人體內(nèi)毒素的排出，有促進人體細胞的生成以及保持皮膚細嫩等作用。

由此可以得到三維自由旋渦上表面圖（如圖6所示）.

圖6　三維自由旋渦上表面

從圖6中可以看出，該模型較好地模擬出了液體旋渦的表面凹陷，并且描述其中心空氣管會伸向無窮遠即伸出排水口.但是在渦心r=0處速度為無窮大是不合理的，因而在半徑較小處該模型會失真［1，2］.但是對于低粘度流體，這種效應的影響不明顯.

2　等角速度轉(zhuǎn)動模型對靠近渦心處的修正

2.1蘭金渦模型［2-4］

蘭金渦是一種旋渦模型，認為旋渦是自由渦與強迫渦的復合，提出了渦核半徑rm的概念.在內(nèi)區(qū)域內(nèi)區(qū)（r≤rm），有旋流，屬強迫渦運動；外區(qū)（r＞rm），無旋勢流，各圓周上Γ相等，屬于自由渦運動（如圖7所示）.

蘭金渦模型也是一種廣為應用的旋渦模型，但其并不能用來描述排水旋渦，因為其未考慮水流的徑向速度.但是該模型引入了渦核半徑的概念，并以此為界線，使用兩個不同的模型描述旋渦，避免了渦心處速度為無窮大的荒謬結(jié)論.將這一方法應用于本文進一步修正上述自由旋渦模型在渦心處的奇異情形.

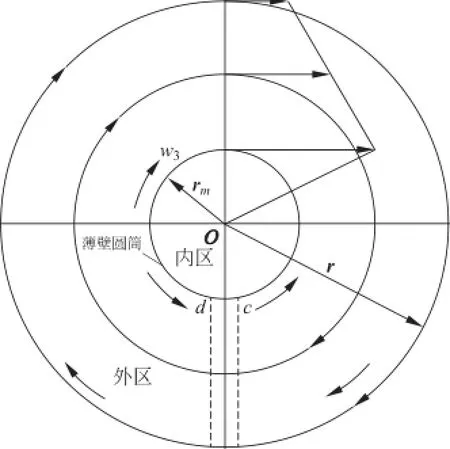
圖7　蘭金渦示意圖［2-4］

2.2等角速度轉(zhuǎn)動模型

由于自由旋渦模型中并未考慮粘滯阻力的影響，而事實上靠近渦心處，液體的速度較大，粘滯阻力已經(jīng)成為一個不可忽略的因素.在粘性阻力的限制下，液體的角速度會有一個上限.因而，不妨設一臨界半徑r0（如圖8所示），當r≤r0時，液體達到粘性阻力限制下的最大角速度，因而在內(nèi)部做等角速度轉(zhuǎn)動，徑向速度為零.而當r＞r0時，仍忽略粘性阻力的影響，采用自由旋渦模型.

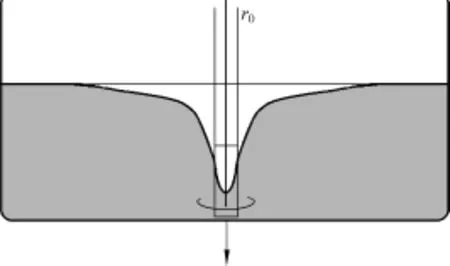
圖8　三維旋渦圖

2.3等角速度轉(zhuǎn)動模型的速度與壓強分布［1，5］

等角速度轉(zhuǎn)動模型如圖9所示，一圓柱形容器繞軸線以角速度ω轉(zhuǎn)動，內(nèi)盛粘性流體，當達到穩(wěn)定狀態(tài)后液體將呈現(xiàn)等角速度轉(zhuǎn)動，液面也將下凹.此時的速度分布有

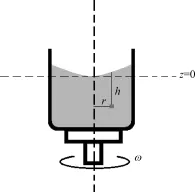
圖9　等角速度轉(zhuǎn)動模型

其中，z′坐標的零點取在下凹表面的最低點.

考察其上表面形狀，令p=p0，則曲面方程為

為一旋轉(zhuǎn)拋物面形.

2.4等角速度模型在渦心處的修正

引入一個臨界半徑r0（其取值會與液體粘度和排水孔的大小相關(guān)），分別在臨界半徑兩側(cè)應用自由旋渦模型和等角速度轉(zhuǎn)動模型，并認為半徑內(nèi)的液體是在r0液體層的驅(qū)動下做等角速度轉(zhuǎn)動.因而其速度分布與壓強分布都是一個分段函數(shù).其液體上表面也是兩個曲面的拼接，計算結(jié)果如圖10所示.

可以看出，該模型修正了渦心處的情形，有了較合理的解釋，同時，給出了高粘度流體在形成旋渦時，液體上表面是一個封閉曲面，而不會總有空氣管伸入排水口的情形發(fā)生.

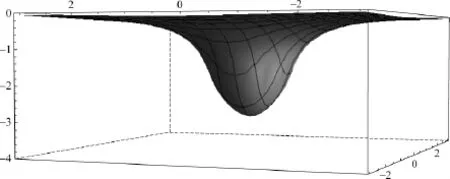
圖10　渦心修正后的液體上表面形態(tài)

3　總結(jié)與應用展望

本文提出的三維自由旋渦理論對低粘度下非靠近渦心的情形有較好的描述，但是其在中心點將失去意義.而本文引入一個臨界半徑，利用粘性作用下的等角速度轉(zhuǎn)動模型，可以避免中心點的奇異性，并對于粘度較高的流體旋渦也能進行一定的解釋.

但到目前為止，實驗對于理論的驗證還處于定性的層面，該理論的準確性還需要通過實驗精準地測定流體內(nèi)部壓強與速度分布，以對不同粘度流體的情形.本文未給出臨界半徑r0的經(jīng)驗公式，同樣，需要大量的實驗進行精準的測定.

旋渦是實際中很常見的一種現(xiàn)象，在工業(yè)中有一定的危險性，因為旋渦的形成會減少進流量、降低流量系數(shù)；引起機械振動；降低機組效率，強烈的吸氣旋渦可降低機組工作效率；卷吸水面漂浮物、造成攔污柵堵塞或損壞［1］.因而旋渦的研究意義重大，還有許多問題值得深入的研究與探索.

［1］ 景思睿，張鳴遠.流體力學［M］.西安：西安交通大學出版社，2001.

［2］ 杜敏.進水口漩渦形成機理及縮尺效應.天津大學建筑工程學院，博士論文，2008.

［3］ 趙永志，顧兆林，郁永章，等.盆池渦渦動過程數(shù)值研究［J］.水利學報，2002（12）：1-6.

［4］ 趙永志，顧兆林，郁永章，等.自由水渦結(jié)構(gòu)及運動特征的數(shù)值研究［J］.西安交通大學學報，2003（1）：85.

［5］ 黃楚迪，王奔，盧志健，等.暗流和漩渦的壓強分布簡化物理模型研究［J］.科技創(chuàng)新導報，2013（24）：67-70.

DISTRIBUTION OF PRESSURE AND VELOCITY IN THE VORTEX APPEARING NEAR A DRAIN

Fang Aiping Tian Pengbo Sun Dihao Niu Sijun Zhu Minghui Wei Minghua Yu Youli Wang Xiaoli
（School of Science，Xi，an Jiaotong University，Xi，an，Shaanxi 710049）

The research aims at the property of the vortex appearing near a drain in gravitational field.Due to the analysis of the distribution of pressure and velocity in a stable vortex，the shape of its surface can be determined as a concave surface.Similar to the thought of Rankine vortex model，two vortex models are used in the article，divided by a critical radius.Free vortex model is used to simulate the vortex outside the radius.Near the core of the vortex，constant angular velocity model is adopted to avoid the singularity.These models show the patterns of pressure and velocity distribution in a vortex，and explain qualitatively the differences between the shapes of vortexes in liquids with various coefficients of viscosity.

free vortex；Rankine vortex；point sink；point vortex