“加法”的前概念研究

沈百軍

一、加法的認識

合久必分、分久必合，合與分是世界上兩種基本存在形態。從數學的角度來分析，合所對應的是加法，分所對應的是減法，其中等數量的合就是乘法，等數量的分就是除法。再從運算的關系來看，減法是加法的逆運算，除法是乘法的逆運算，由此可知加法是最為基礎的運算，是其他運算的基石。

按照集合論的觀點，兩個自然數a和b相加的和為a+b，是指如果a和b分別是互不相交的兩個集合A和B的基數，那么，a和b所代表的集合A、B是互不相交的，而a+b則是并集A∪B的基數（《小學數學研究》第26頁）。在小學階段，加法的含義就是指兩部分的合并，也可以說加法是對一類客觀現實中具有合并現象的數學化表征。例如，左手有3顆糖果，右手有2顆糖果，合起來是5顆，寫成數學算式就是3+2=5。小學生建立加法概念需要借助具體的生活情境和操作活動，孔企平老師在《小學數學課程和教學論》一書中說得非常明確，具體情境是小學生理解加減法的基礎，當一個數的運算與代表情境中的物體相聯系時，才能在學生的頭腦中獲得真正的意義。

二、學生已有經驗的分析

現行教材都把“加法的認識”這一內容放在一年級上冊，緊接在“5以內數的認識”之后進行的教學。一年級剛入學的學生大多是六周歲半左右，那么，這一年齡段的學生對加法有哪些認識呢？

（一）生活中關于加法經驗的積累

加法作為一種生活現象司空見慣，隨處可見，兒童的成長過程中經常會遇到并經歷具有加法含義的活動。嬰兒從出生到上小學的六年多時間中，天天會遇到具有加法意義的生活現象，如：

現象1：家里有爸爸、媽媽和小貝，今天外婆來了，家里就多了一個人。

現象2：小貝已經有2輛玩具車了，今天叔叔又送給他一輛嶄新的玩具車，現在有3輛玩具車了。

現象3：小貝喜歡畫畫，上午畫了3個小動物，下午又畫了2個小動物，數一數，總共畫了5個小動物。

上述現象都是兩部分的合并，也就是都具有加法結構的模型。孩子從出生到上幼兒園常常會遇到或發生類似與加法有關的事情，學生在不知不覺中已經積累了關于加法的直觀感知，至少能夠正確判斷多了還是少了。

（二）知識學習過程中積累的加法經驗

盡管上小學之前，兒童還沒有明確的要求需要學習一定的知識和技能，但受望子成龍、望女成鳳的思想觀念影響，讓孩子盡早地識字認數、會數數、會做加減運算是多數家長的殷切期望，因此學生的學習已經先于學校教育而開始。

首先，多數兒童在上學前學會了數數，尤其是能夠指著具體的實物進行點數，也就積累了最為原始的加法運算的能力。

其次，在幼兒園孩子要認識很多圖形，做很多活動和基礎性的練習，從中會有不少與加法運算有關的內容，如：

湊數活動：小朋友心中想好一個確定的數，然后從1～10這十張撲克牌中找出兩張，使得兩張牌的點數正好湊成心中確定的數。

打靶游戲：在靶上標出1～5這五個數字，小朋友用沙包打靶兩次，并把兩次打中的分數加起來作為最后的成績。

6以內的加減運算練習：小朋友吃掉5瓶果奶，還剩下1瓶果奶，活動室里原來有幾瓶果奶？

[注：以上活動和習題均出自浙江省《幼兒園課程指導》編寫委員會編寫的《大班教育活動設計（上冊）》，新時代出版社出版。]

三、前測的意圖及習題

從上述的分析來看，學生有比較豐富的生活經驗和知識儲備，但就每個個體而言，對加法的感知是否如上所說，他們當中存在著怎樣的差異呢？為了更好地幫助學生學習并建構加法的概念及基本的運算技能，我們試圖通過前測了解學生以下幾個方面的現實起點，從而為教學提供有利的資源和借鑒。

第一，學生面對兩部分合并的情境時，會自覺運用加法計算的占多大比例？

第二，學生正確進行10以內加法運算的比例如何？

第三，學生對加法含義的理解達到何種程度？能否用具體的動作和直觀圖示進行表征？

第四，面對具體的現實情境，學生能否借助加法運算進行解答？

基于這樣的意圖，為了便于操作，我們設計了如下前測題：

四、測試要求和數據統計

（一）測試的對象

一年級學生120人，在開學初第一周或第二周完成。（為了對比研究，可以選幼兒園大班學生進行測試）

（二）測試的方法

統一采用面試。先做好測試題課件（包括錄音），逐一對學生進行面試，有條件的可以錄像，但不要對學生產生影響。

（三）數據統計

每個測試題需要統計的數據：

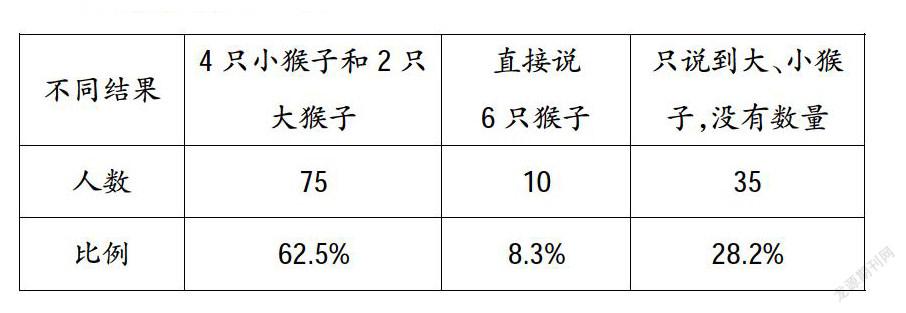
測試題1：（1）正確說出大、小猴子數量的人數及比例；（2）正確說出結果是6只的人數及所占的比例。

測試題2：（1）正確表述題意并算出結果的人數及比例；（2）在同一情境下不同算法的人數和比例。

測試題3：（1）口算結果正確的人數及比例；（2）會正確表征兩部分之和的人數及比例。

測試題4：（1）正確判斷是否夠的人數及比例；（2）不同方法解決這個問題的人數及比例。

五、測試結果分析和教學建議

（一）測試結果（一年級剛入學初）

我們選擇了城區中心小學和鄉鎮小學共6所120名剛入學的一年級新生進行了前測，其結果如下：

測試題1：課件出示靜態圖：左邊4只小猴子，右邊2只大猴子。

（1）你看到了什么？

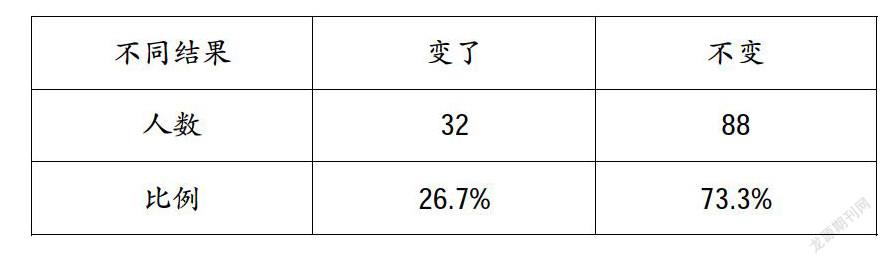
（2）課件中變化猴子的位置，問學生總數是否變了，為什么？

絕大多數學生還能正確說出不變的原因：只是猴子的位置變了，還是6只（或者4小2大）猴子，少數學生因為不理解“總數”的含義，未能正確回答。

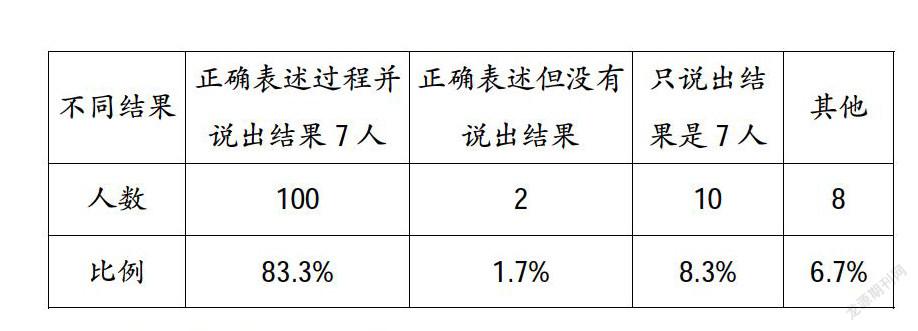
測試題2：課件出示5個學生，動態演示又來了2個學生。

（1）用語言表述：你看到了什么？

（2）你是怎么算的？

測試題3：口答2加3等于多少？請用身邊的實物或是動作來表示2加3。

（1）120人正確回答結果是5的，占100%。

（2）用身邊的實物或動作表示2+3的如下表所示：

測試題4：小明的媽媽有3元錢，小明的爸爸有5元錢。他們要買一本7元錢的圖畫書給小明，夠嗎？（有課件和語音）

（1）有119人回答錢夠了，占99.2%。

（2）在119人中，有23人是通過數的方法獲知還多出1元；有82人是通過先加（3+5=8），然后與7比較，認為多出1元；還有12人通過計算（3+4=7）比父母的總錢少1元來判斷的；只有2人不會說其中的原因。

（二）測試結果分析

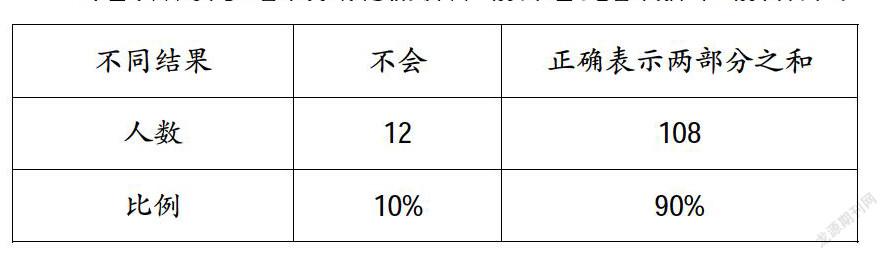
第一，一年級剛入學的學生已經具備了簡單的加法運算能力，特別是5以內數的加法正確率很高。

第二，一年級新生對加法有了比較全面的直觀理解：一是知道兩部分合并可以用加法來計算；二是對一個加法算式能用不同的直觀圖示來表征，初步具備了數學符號化的意識；三是在面對具體問題時，多數學生已經具備了先加再比的策略意識。

第三，在計算5+2、3+5等算式時，尚有20%左右的學生采用了數的方法，而且從1開始數的占到一半左右。

第四，學生對加法意義的理解是淺層次的，對加法所具有的高度抽象性和概括性的認識還不夠深入。

第五，通過對幼兒園大班兒童的前測，兩者之間的差距不是很大，主要在兩個方面存在一些差異：一是一年級新生在表達上要稍稍高出大班兒童，如第二題，看課件演示能正確表述過程并說出結果是7人的，一年級新生高達83.3%以上，而大班兒童只有41.7%。二是一年級新生在解決具體問題（如測試題4）時，直接用算式解決的比例要高于大班兒童。

第六，城區學校、鄉鎮學校和山區學校之間沒有明顯的差異。

（三）教學建議

根據前測數據分析，我們對加法初步認識一課的教學提出如下建議。

第一，這是一節以建立“加法”概念為主的概念教學課，而非很多教師認為的加法計算教學課。

第二，這節課的重點是讓學生在豐富的現實情境中真正理解加法的含義，而不是進行加法算法的探究。在具體計算時，只需要引導學生正確數就可以了。如3+1，就是在3的基礎上繼續往下數得到4；同理，4+2就是在4的基礎上繼續往下數到6。

第三，應該讓學生理解加法算式的表征作用，初步感受數學抽象的魅力。要讓一年級學生經歷一個從具體情境到抽象算式的歸納抽象過程，還要讓學生展開想象，看到算式能想到不同的具體情境，從而比較深刻地理解加法的本質含義。教師需要為學生提供不同的素材（如靜態的：左邊3個蘋果右邊1個蘋果，樹上3只猴子樹下1只猴子；還可以是動態的：停車場原來有3輛汽車，又開來了1輛汽車），讓學生表達并寫出算式“3+1=4”，然后根據算式“3+1=4”來編類似的故事情境（如媽媽給我3顆奶糖，爸爸又給了我1顆，我一共得到了4顆奶糖）。有了這樣豐富而完整的學習經歷，學生才能漸漸體會數學算式不再只是一個算式，而是具有豐富的內涵，也逐漸體悟到數學的高度抽象性。這樣的學習過程，不僅學到了知識，而且還很好地滲透了數學思想方法，讓小學生從小經歷數學抽象、數學歸納和數學演繹，而這些正是最為基本的數學思想方法。

第四，一年級學生的數學學習需要動手、動眼、動口、動腦，創設情境讓學生主動參與，特別是要把學生看到的、動手做的表達出來，表達的方式除了用語言，還要用表象和抽象的符號和算式。表達的過程就是思維內化的過程，也是學生思考不斷深入的過程。

（浙江省寧波市鄞州區東裕小學 315100）