水平軸風力機多渦格升力面渦尾跡法的研究

王淵博，李春,2，欒忠駿

(1.上海理工大學 能源與動力工程學院，上海 200093； 2．上海市動力工程多相流與傳熱重點實驗室，上海 200093)

?

水平軸風力機多渦格升力面渦尾跡法的研究

王淵博1，李春1,2，欒忠駿1

(1.上海理工大學 能源與動力工程學院，上海 200093； 2．上海市動力工程多相流與傳熱重點實驗室，上海 200093)

針對NREL Phase VI實驗雙葉片水平軸風力機，采用基于多渦格升力面的自由尾跡法模擬其低風速及高風速氣動性能。由于高風速失速延遲導致尾緣分離滯后，建立Kirchhoff-Helmholz尾緣分離預估模型與Du-Selig失速延遲模型耦合的三維尾緣分離預估模型。計算低風速及高風速不同的偏航角工況，對比分析不同渦格數對模擬結果的影響。研究結果表明：渦格數對低風速工況影響甚小，對高風速影響很大，且采用兩渦格的三維尾緣分離預估模型對法向力系數和弦向力系數的模擬最為精確。

水平軸風力機；多渦格升力面；自由渦尾跡；渦格數；偏航；失速延遲；尾緣分離

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20160624.1127.014.html

為準確預估水平軸風力機在不同風速工況下所受氣動力及氣動力矩，以提高風力機設計水平，建立準確的氣動模型是其根本前提[1]。常用的風力機氣動研究方法有：動量葉素法[2]、渦尾跡法[3-4]和基于求解N-S方程的CFD方法。渦尾跡法計算精度高于動量葉素法，計算效率優于CFD方法，可準確用于計算低速不可壓流動[5]。其中，自由尾跡法根據尾跡各點合速度更新尾跡位置，能模擬葉尖渦卷起和尾跡畸變現象[6]。文獻[7]基于自由渦尾跡方法對四種動態來流風下的NREL Phase VI風力機性能和結構進行計算，發現非穩態來流風會導致風力機性能下降、疲勞載荷增加。文獻[8]采用非線性升力面方法，建立軸向和偏航風條件下的水平軸風力機氣動載荷及尾跡的數值模擬方法，證明了該方法可實現較好的工程數值模擬。文獻[9]利用渦尾跡方法進行風力機氣動載荷計算，結果表明大型風力機葉片幾何非線性可較為明顯地減小靜氣動彈性位移，同時降低動氣動彈性的響應幅值。以上研究均采用單渦格升力面模型，當葉片弦長較大時誤差較大，而本文時間步進自由尾跡法采用多渦格升力面模型，可精確模擬大弦長葉片的氣動性能。此外，由于渦尾跡法基于不可壓縮勢流理論[10]，物面邊界方程認為葉片表面流動不發生分離，適用于低風速小攻角工況，而對于高風速大攻角工況，葉片尾緣流動將發生分離，且分離點受三維旋轉效應影響發生滯后現象，文獻[7-9]并沒有考慮這一問題。針對高風速大攻角工況，筆者建立了Kirchhoff-Helmholz尾緣分離預估模型[11]與Du-Selig三維失速延遲模型[12]耦合的三維尾緣分離預估模型，考慮高風速下各徑向位置尾緣流動分離情況，并通過引入分離角偏轉矩陣對原物面邊界方程做出相應修正。在此基礎上分別計算不同渦格數對各工況氣動性能的影響，得到葉片最佳渦格數布置。

1　多渦格升力面模型

采用離散的渦分布升力面模型，即所謂渦格法(vortex lattice method, VLM)，將葉片分為徑向和弦向若干個渦格，環量沿徑向和弦向都存在變化，更好的描述了葉片表面的三維流動。

升力面渦格法網格劃分采用在葉片弦向布置M個渦格，徑向布置N個渦格[5-6]，如圖1所示。沿徑向的渦線為附著渦，弦向的渦線為自由渦，控制點布置在渦格中心。每個渦格四條渦線具有相同環量值，渦格環量方向根據右手定則與渦格法向量同向。

圖1　葉片升力面渦格劃分Fig.1　Vortex lattice distribution of blade lifting surface

渦尾跡法通過對每個渦格控制點滿足物面邊界條件求解葉片渦線環量。對于低風速工況，滿足原物面邊界方程式(1)即可:

(1)

式中：Vk為相對來流速度，Vind為尾跡及葉片渦線對控制點的誘導速度，n為渦格的法向量。對于高風速工況，需引入分離因子f進行修正，其定義為分離點距尾緣的弦向距離與弦長的比值，如圖2所示。數值模擬時，對于高風速10m/s，取分離角為5°。

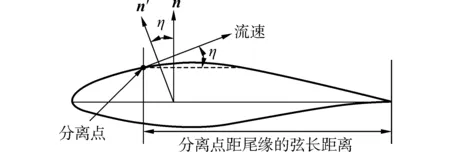
圖2　高風速葉片尾緣流動分離示意圖Fig.2　Trailing edge separation of high wind speed

在圖2尾緣分離的情況中，分離點之前的渦格運用式(1)即可，而對于分離點之后的渦格，原物面邊界方程已不適用。假設流動分離角η，將原法向力旋轉分離角η，得到n′，令合速度與之垂直，通過在原物面邊界方程中引入一分離角η偏轉矩陣，以滿足尾緣流動分離求解環量。修正后的物面邊界方程：

(2)

為考慮粘性對誘導速度的影響，且避免計算誘導速度時出現奇值，采用Lamb-Ossen渦核模型，并引入時間補償參數改變渦核起始半徑，式(3)為隨時間增大的渦核半徑：

(3)

式中：α為經驗系數，取常數1.256 43；ν為空氣運動粘度；t為時間。根據文獻[13]，時間補償參數Sc取值0.1，擾動粘性系數δν取100。

2　三維尾緣分離預估模型

對于高風速工況，為考慮葉片尾緣分離，準確計算出葉片各徑向位置分離點的位置，建立了Kirchhoff-Helmholz尾緣分離預估模型與Du-Selig失速延遲模型耦合的三維尾緣分離預估模型。

2.1Du-Selig三維失速延遲模型

文獻[14]對比了6種三維失速延遲模型，其中Du-Selig模型的預測結果與實驗值吻合最好，因此，本文采用該模型考慮風力機三維旋轉效應。

Du和Selig通過求解旋轉坐標系下風力機葉片表面三維積分邊界層方程，在二維翼型升、阻力系數上添加一個增量進行三維修正：

(4)

(5)

式中：Cl,2D和Cd,2D分別為二維升、阻力系數；Cl,P=2π(α-α0)，α0為零升力攻角，α為實際攻角；Cd,0為二維零攻角阻力系數。經過與實驗數據的關聯，得到上式中fl、fd經驗修正系數：

(6)

(7)

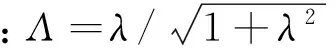
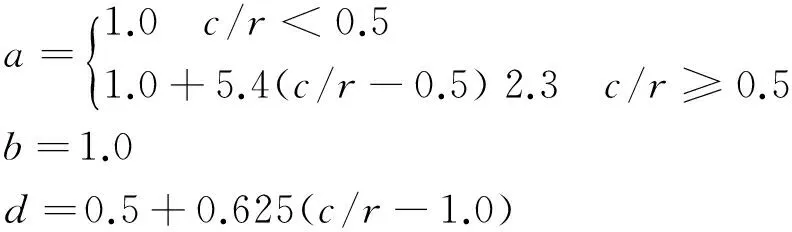
(8)

采用NRELPhaseVI實驗葉片[15]為算例，以OSU大學在雷諾數Re=106下所測S809翼型的二維升、阻力系數實驗數據為基礎，在V=10 m/s，Ω=72 r/min工況下，將葉片各徑向位置處弦長、當地尖速比代入式(4)和式(5)，計算經過Du-Selig三維失速延遲模型修正后的葉片各徑向位置升、阻力系數，得到圖3。分析三個徑向位置，葉片無量綱半徑(r/R)分別為0.3、0.47和0.8。

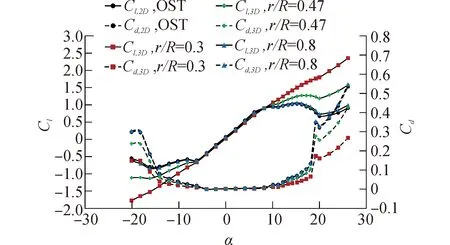
圖3　Du-Selig模型修正后的三維升、阻力系數Fig.3　3D lift and drag coefficient corrected with Du-Selig model

從圖3可知，Du-Selig三維失速延遲模型對小攻角線性增長區幾乎無影響，而對于大攻角失速區，從葉尖到葉根，三維失速延遲模型的修正效果增強。

對于r/R=0.3，在大攻角失速區，升力系數幾乎隨攻角增大一直保持增長趨勢，阻力系數相對原二維翼型阻力系數也降低很多，說明葉片徑向流動對靠近葉根處的作用最為明顯，尾緣分離點得到很大程度的推移；在r/R=0.45中間葉高處，失速攻角相應推遲，升力系數明顯增大，阻力系數也相應減小；在r/R=0.8接近葉尖處，三維修正后的升、阻力系數與二維實驗數據幾乎一致，說明葉尖處周圍流場影響較大，葉片徑向流動效果明顯減弱，幾乎不造成尾緣分離點的推移。

2.2Kirchhoff-Helmholz尾緣分離預估模型

Kirchhoff-Helmholz模型基于二維翼型氣動力系數，尾緣分離因子f可表示為翼型法向力系數Cn,2D的函數：

(9)

式中：α為當地攻角，α0為零法向力系數對應攻角，Cn,0對應法向力系數為零處的梯度。

將Kirchhoff-Helmholz尾緣分離預估模型與Du-Selig三維失速延遲模型耦合，考慮三維旋轉情況下葉片徑向流動對尾緣分離點位置的影響。在上節對升、阻力系數進行三維失速延遲修正后，通過下式得到相應修正后的三維法向力系數：

(10)

將Du-Selig模型得到的三維法向力系數Cn,3D代替式(9)Kirchhoff-Helmholz模型中的翼型二維法向力系數Cn,2D，得到耦合后的三維失速延遲特性的尾緣分離預估模型，用Kirchhoff-DuSelig模型代稱。計算二維Kirchhoff-Helmholz模型及耦合后的三維Kirchhoff-DuSelig模型尾緣分離因子隨攻角變化規律，并與二維翼型風洞實驗數據[16]進行對比，如圖4所示。

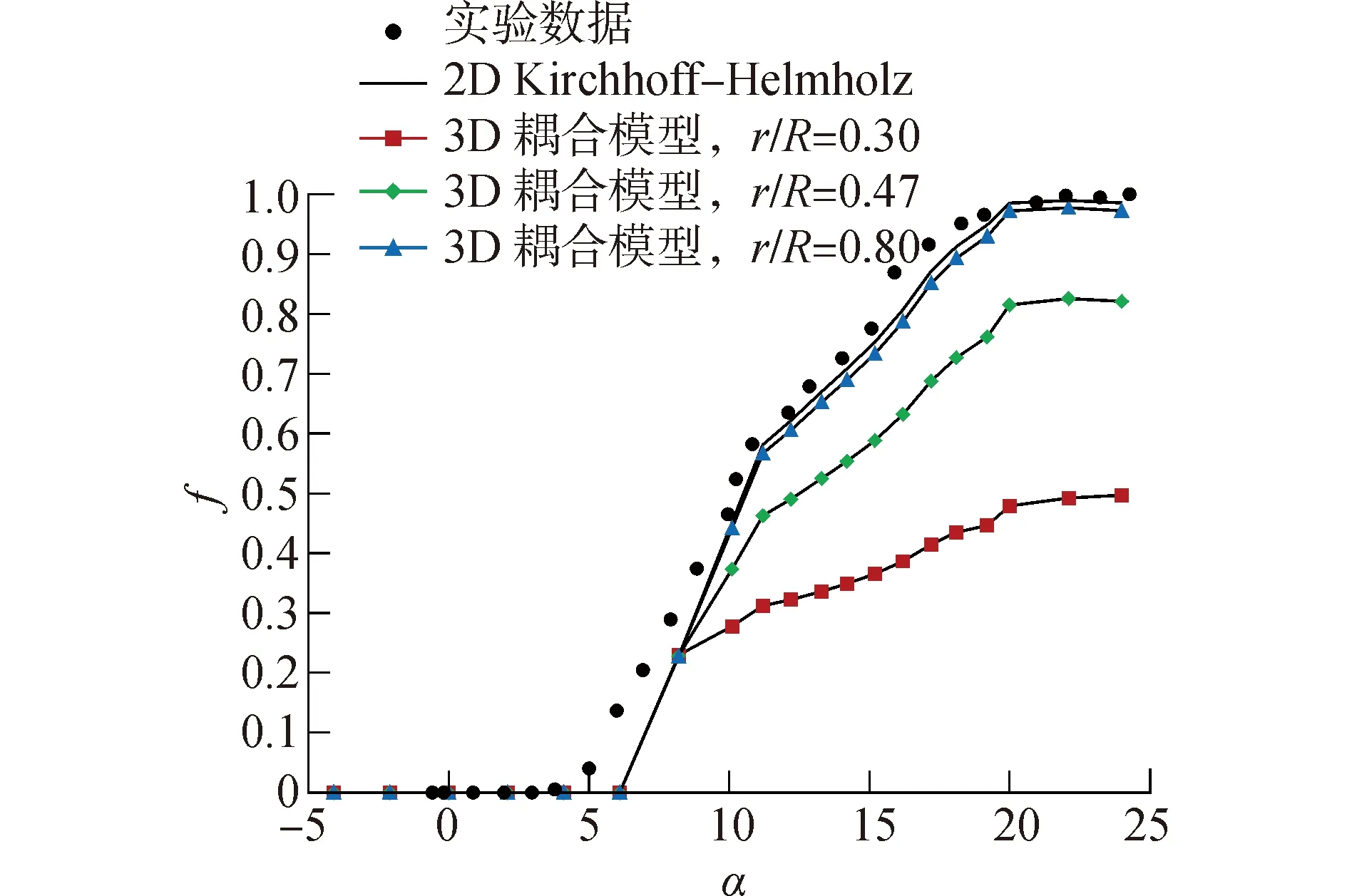
圖4　預估模型分離因子Fig.4　Separation factor of prediction models

從圖4可知，二維Kirchhoff-Helmholz模型分離因子與實驗值非常接近，說明不考慮三維旋轉效應時，Kirchhoff-Helmholz模型可準確模擬大攻角時二維翼型尾緣分離點位置。而耦合后的三維尾緣分離預估模型在不同徑向處的分離因子與二維預估模型各不相同，體現出實際三維旋轉效應使得葉片各徑向位置的尾緣分離有不同程度的推移。攻角為-5°～8°，二維和三維耦合模型的分離因子相同，因為攻角在8°之前，升、阻力系數處于線性增長區，Du-Selig模型對升、阻力系數無影響，如圖3所示。且在攻角小于6°時，分離因子都為0，尾緣流動不發生分離。隨著攻角增大，分離因子相應增大，則尾緣流動分離發生的越快。

在r/R=0.3處，分離因子增大的幅度很小，因為葉片徑向流動引起失速延遲現象，分離點推移，在靠近葉根處尤為明顯。在r/R=0.8處，三維耦合模型的分離點預測幾乎與原始二維模型一樣，說明在靠近葉尖處，尾緣分離情況與二維翼型相差不大，沒有發生明顯的失速延遲現象。

3　低風速氣動性能模擬

以NRELPhaseVI實驗雙葉片風力機為研究對象，葉片長5.03m，槳距角3°，風輪轉速72r/min，葉片弦長及扭角數據參考文獻[15]。計算風速5m/s，偏航角θ分別為10°、30°、45°和60°工況，葉片弦向渦格數M分布采用1、2和3，得到不同渦格數所模擬的葉片徑向法向力系數Cn和弦向力系數Ct，圖5為模擬值與實驗數據對比圖。

(a)V=5 m/s ,θ=10°

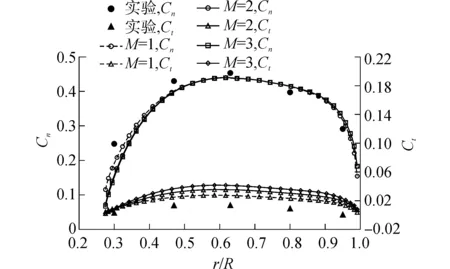
(b)V=5 m/s, θ=30°

(c)V=5 m/s ,θ=45°

(d)V=5 m/s ,θ=60°圖5　風速5 m/s時不同偏航角徑向Cn和Ct分布Fig.5　Normal force and tangent force coefficient of 5 m/s wind speed under different yaw angle

由圖5可知，多渦格升力面法對低風速氣動性能的模擬值與實驗值吻合度很高。隨著偏航角增大，徑向法向力系數和弦向力系數減小，尤其當偏航角為60°時，能夠模擬出靠近葉根處出現負攻角導致的負法向力系數，說明渦尾跡法對低風速氣動性能的模擬精度很高。升力面采用不同的渦格數，對低風速模擬結果影響不大，因為低風速時，有效攻角很小，葉片尾緣未發生分離，弦向采用一個渦格已可準確表示葉片附著渦環量，亦無需采用三維尾緣分離預估模型求解分離點位置。

4　高風速氣動性能模擬

4.1葉片氣動力系數

模擬高風速10m/s，偏航角為10°和30°工況，采用基于Kirchhoff-DuSelig三維尾緣分離預估模型多渦格升力面法，渦格數M分別為1、2和3。圖6對應葉片徑向法向力系數和弦向力系數與實驗數據對比圖。

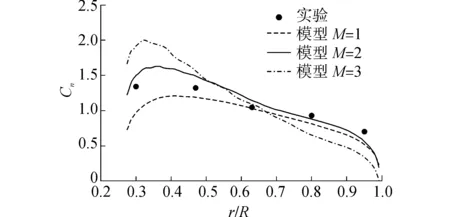
(a)V=10 m/s，θ=10°，Cn

(b)V=10 m/s，θ=10°，Ct

(c)V=10 m/s，θ=30°，Cn

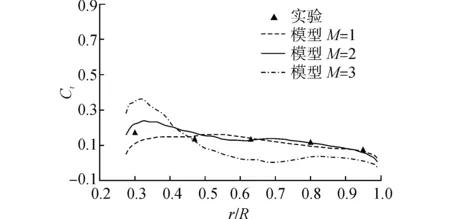
(d)V=10 m/s，θ=30°，Ct圖6　風速10 m/s時不同偏航角徑向Cn和Ct分布Fig.6　Normal force and tangent force coefficient of 10 m/s wind speed under different yaw angle

圖6說明，采用弦向渦格數M=2的Kirchhoff-DuSelig三維尾緣預估分離模型得到的法向力和弦向力模擬值與實驗值吻合度最好。

當弦向渦格數M=1時，只在葉片弦向布置一個渦格略顯粗糙，即認為葉片從1/4弦向處就發生分離，這樣葉片表面分離過早，計算得到的法向力系數相對于實驗值偏小。而Kirchhoff-DuSelig、M=2模型適當的增加了渦格數，更準確的描述尾緣分離點位置，所預測的法向力系數和弦向力系數與實驗值最接近。Kirchhoff-DuSelig、M=3模型在葉片上布置了3個渦格，雖然能更準確的描述尾緣分離點位置，但是葉片上的渦格增多會引起對葉片附著渦誘導速度的增大，尤其是軸向誘導速度，從而導致靠近葉根模擬值偏高，靠近葉尖處模擬值偏低。

當葉片弦長增大時，渦格數需相應增加，具體弦長所對應的M值可通過與實驗或精確CFD模擬結果對比求得。

4.2葉片分離因子

為了清晰直觀地了解風速10m/s時，在不同的偏航角下，葉片表面各徑向位置尾緣分離情況。圖7給出了4個旋轉周期內，在各個方位角葉片徑向尾緣分離因子分布云圖。

圖7表明，各徑向位置尾緣分離因子隨當地攻角呈周期性變化，在靠近葉根處，由于三維旋轉效應引起的失速延遲現象，尾緣分離點后移，分離因子較小，在靠近葉尖處，由于攻角很小，分離因子也較小。而在中間葉高處，失速延遲效應沒有近葉根處明顯，且攻角較大，因此，分離因子最大。而在每個旋轉周期內，分離因子總在90°方位角取得最小值，在270°方位角取最大值，因為在90°方位角，來流速度在x軸的偏航分速度與相對旋轉速度同向，造成攻角大幅減小，尾緣分離減弱。而在270°方位角，來流速度在x軸的偏航分速度與相對旋轉速度反向，造成攻角大幅增大，尾緣分離加強。

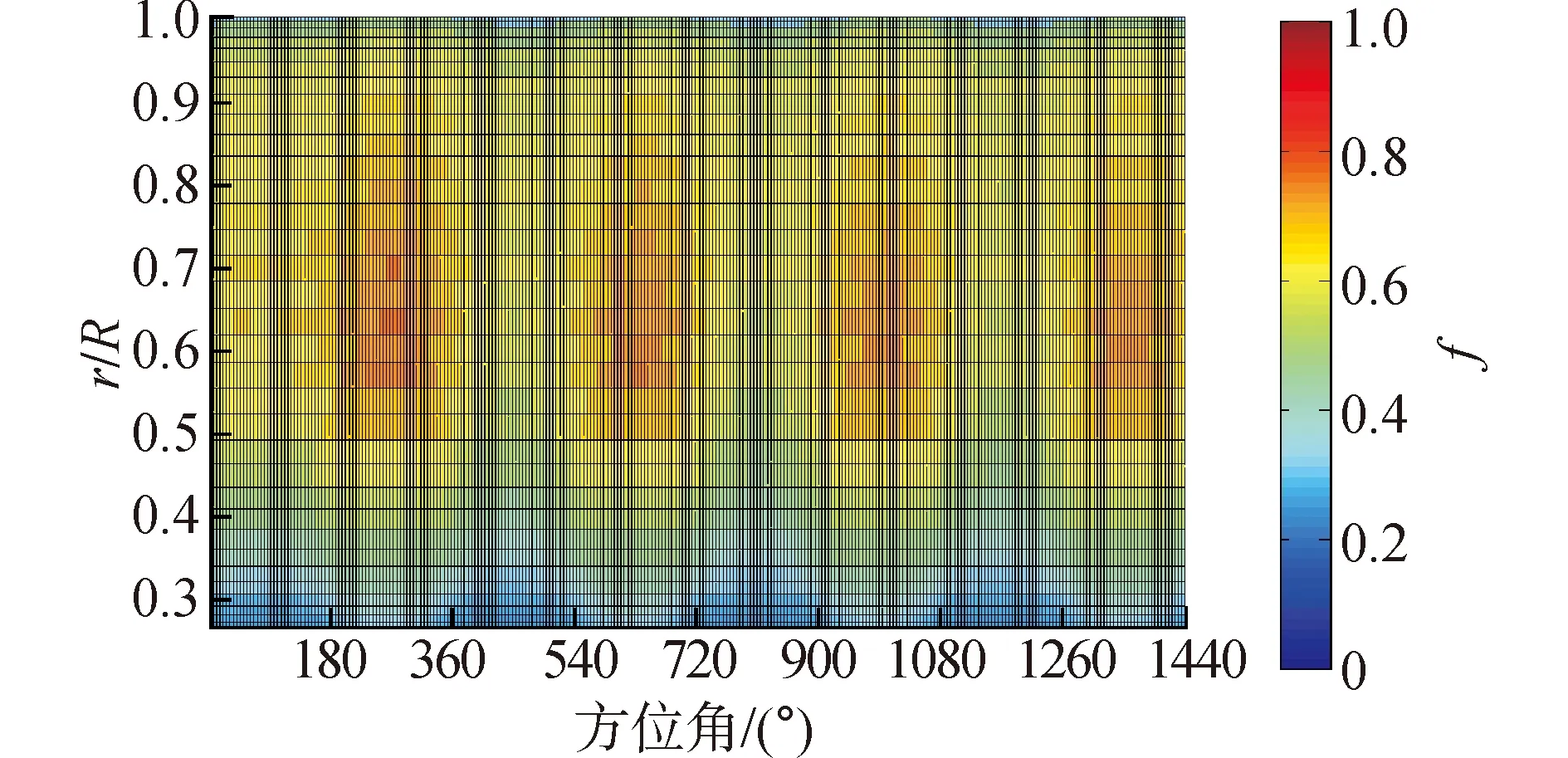
(a)V=10 m/s，θ=10°

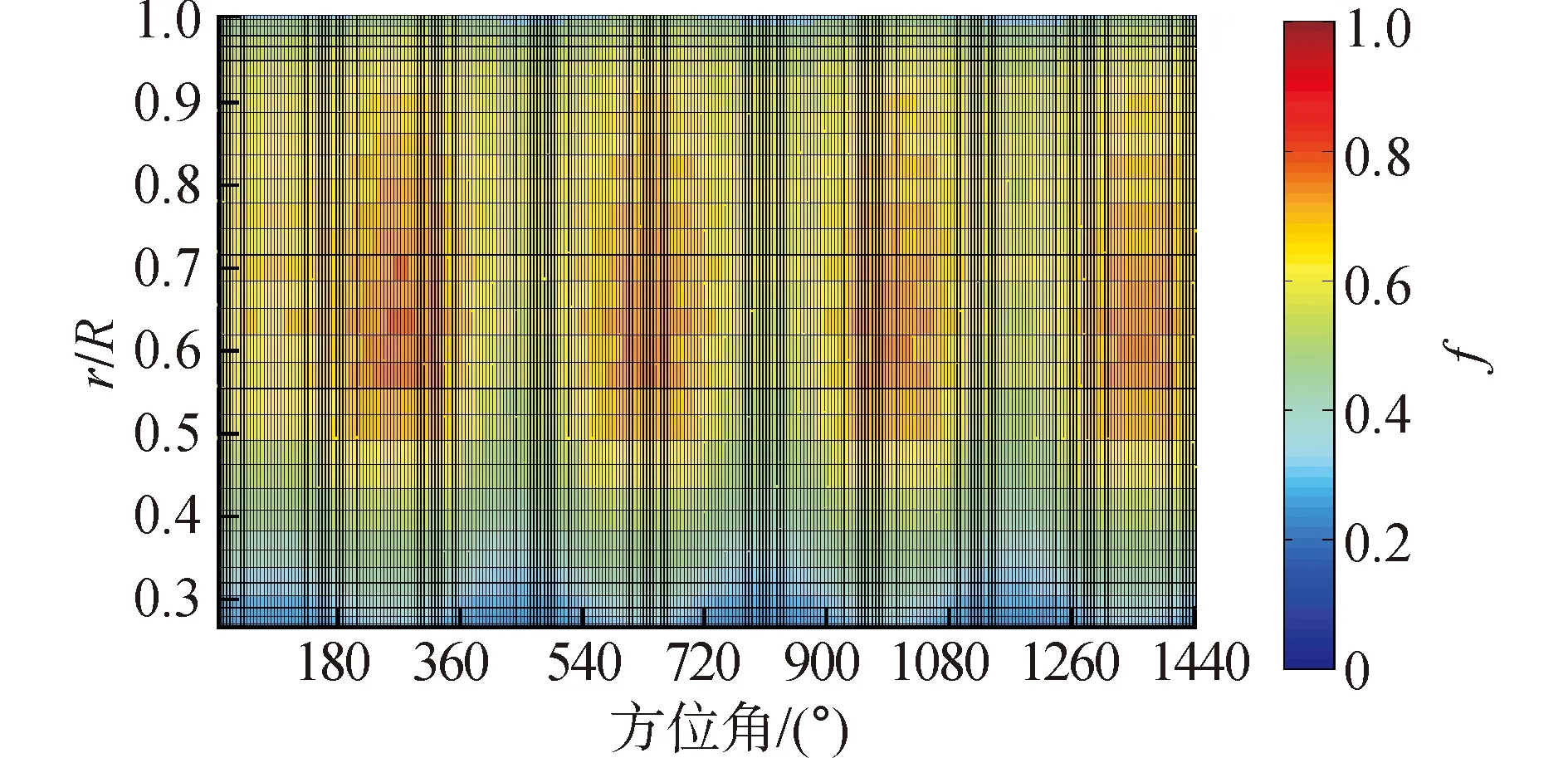
(b)V=10 m/s，θ=30°圖7　風速10 m/s時不同偏航角周向尾緣分離因子分布Fig.7　Azimuthal trailing edge separation factor of 10 m/s wind speed under different yaw angle

4.3葉片氣動力矩

根據圖7中尾緣分離因子隨方位角變化關系，分析尾緣分離因子對葉片主軸扭矩和揮舞力矩的影響。圖8為風速10m/s，偏航角分別為10°和30°，主軸扭矩和揮舞力矩在4個周期內隨方位角變化的關系。

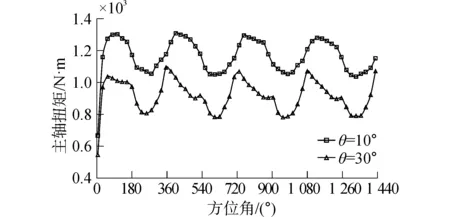
(a)主軸扭矩

(b)揮舞力矩圖8　風速10 m/s不同偏航角主軸扭矩和揮舞力矩Fig.8　Shaft torque and flap-wise moment of 10 m/s under different yaw angle

計算葉片氣動力矩需查詢升阻力系數表，其中升力系數呈正弦分布，阻力系數不呈正弦分布，由于攻角較小，揮舞力矩受升力系數影響大，主軸力矩受阻力系數影響大，因此揮舞力矩呈正弦波動，而主軸扭矩呈鋸齒狀周期波動。此外，隨著偏航角的增大，主軸扭矩和揮舞力矩相應減小，受圖7中尾緣分離因子的影響，主軸扭矩在方位角90°左右取最大，在方位角270°左右尾緣分離較劇烈，扭矩值最小，因此，Kirchhoff-DuSelig三維耦合尾緣分離預估模型較準確地預估了不同方位角各徑向位置尾緣分離點，從而表現出尾緣分離情況對主軸扭矩的影響，主軸扭矩直接影響風力機的輸出功率。

5　結論

1)多渦格升力面模型對低風速工況的氣動性能模擬精度很高，且渦格數對結果影響不大；

2)渦格數對高風速氣動性能模擬結果影響較大，采用兩渦格的Kirchhoff-DuSelig三維尾緣分離預估模型，考慮了尾緣分離所引起的氣動力系數降低，且適當增加渦格能準確地表示尾緣分離點位置，模擬結果與實驗值最為接近。

3)得出風速10m/s時不同偏航角下，葉片徑向分離因子隨方位角分布規律。中間葉高處分離因子較大，且在每個旋轉周期內，分離因子在90°方位角最小，在270°方位角最大，因此，葉片主軸扭矩在270°方位角輸出最小。

[1]李春, 葉舟, 高偉, 等. 現代大型風力機設計原理[M]. 上海: 上海科學技術出版社, 2013: 110-147.

LI Chun, YE Zhou, GAO Wei, et al. Modern large-scale wind turbine design principle[M]. Shanghai: Shanghai Scientific and Technical Publishers, 2013: 110-147.

[2]OKULOV V L, VAN KUIK G A M. The Betz-Joukowsky limit: on the contribution to rotor aerodynamics by the British, German and Russian scientific schools[J]. Wind energy, 2012, 15(2): 335-344.

[3]KOMNINOS K. Modeling considerations of the optimum rotor using vortex method[D]. Denmark: Technical University of Denmark, 2008: 7-119.

[4]SHENKAR R. Design and optimization of planar and nonplanar wind turbine blades using vortex methods[D]. Denmark: Technical University of Denmark, 2010: 1-86.

[5]BOUATEM A, ALMERS A, BOUTAMMACHTE N. Load evaluation of horizontal-axis wind turbine rotor using coupled Beddoes near-wake model and free-wake method[J]. International journal of energy and environmental engineering, 2013, 4: 35.

[6]CHKIR S. Unsteady loads evaluation for a wind turbine rotor using free wake method[J]. Energy procedia, 2011, 6: 777-785.

[7]周文平, 唐勝利, 呂紅. 風剪切和動態來流對水平軸風力機尾跡和氣動性能的影響[J]. 中國電機工程學報, 2012, 32(14): 122-127.

ZHOU Weiping, TANG Shengli, LV Hong. Effect of transient wind shear and dynamic inflow on the wake structure and performance of horizontal axis wind turbine[J]. Proceedings of the CSEE, 2012, 32(14): 122-127.

[8]仇永興, 康順. 基于非線性升力面方法的風力機尾跡數值模擬[J]. 工程熱物理學報, 2012, 33(12): 2072-2075.

QIU Yongxing, KANG Shun. Numerical simulation of wind turbine wake based on nonlinear lifting surface method[J]. Journal of engineering thermophysics, 2012, 33(12): 2072-2075.

[9]唐迪, 陸志良, 郭同慶. 大型水平軸風力機葉片氣動彈性計算[J]. 應用數學和力學, 2013, 34(10): 1091-1097.

TANG Di, LU Zhiliang, GUO Tongqing. Aeroelastic analysis of large horizontal axis wind turbine blades[J]. Applied mathematics and mechanics, 2013, 34(10): 1091-1097.

[10]陳浩, 張亮. 漂浮式潮流電站載體水動力性能分析[J]. 應用科技, 2014, 41(1): 65-68.

CHEN Hao, ZHANG Liang. Hydrodynamic performance analysis of floating current power station[J]. Applied science and technology, 2014, 41(1): 65-68.

[11]LEISHMAN J G, BEDDOES T S. A generalised model for airfoil unsteady aerodynamic behaviour and dynamic stall using the indicial method[C]//Proceedings of the 42nd Annual forum of the American Helicopter Society. Washington DC, 1986: 243-265.

[12]杜朝輝. 水平軸風力渦輪設計與性能預估方法的三維失速延遲模型——Ⅲ. 模型改進[J]. 太陽能學報, 2000, 21(2): 145-150.

DU Zhaohui. A 3-D stall-delay model for HAWT performance prediction: Ⅲ. model improvement[J]. Acta energiae solaris sinica, 2000, 21(2): 145-150.

[13]SANT T, VAN KUIK G, VAN BUSSEL G J W. Estimating the angle of attack from blade pressure measurements on the NREL phase VI rotor using a free wake vortex model: axial conditions[J]. Wind energy, 2006, 9(6): 549-577.

[14]許波峰, 王同光, 張震宇. 風力機三維旋轉效應模型研究[J]. 太陽能學報, 2014, 35(4): 562-567.

XU Bofeng, WANG Tongguang, ZHANG Zhenyu. Investigation on three dimensional rotational effect model for wind turbine[J]. Acta energiae solaris sinica, 2014, 35(4): 562-567.

[15]Hand M M, Simms D A, Fingersh L J, et al. Unsteady aerodynamics Experiment Phase VI: Wind Tunnel Test Configurations and Available Data Campaigns[M]. Golden, Colorado: National Renewable Energy Laboratory, 2001: 5-45.

[16]SHENG Wanan, GALBRAITH R A M, COTON F N. On the S809 airfoil′s unsteady aerodynamic characteristics[J]. Wind energy, 2009, 12(8): 752-767.

本文引用格式：

王淵博，李春，欒忠駿.水平軸風力機多渦格升力面渦尾跡法的研究[J]. 哈爾濱工程大學學報, 2016, 37(8): 1070-1075.

WANG Yuanbo, LI Chun, LUAN Zhongjun.Research on multi-lattice lifting surface vortex wake method in horizontal-axis wind turbine[J]. Journal of Harbin Engineering University, 2016, 37(8): 1070-1075.

Research on multi-lattice lifting surface vortex wake method in a horizontal-axis wind turbine

WANG Yuanbo1, LI Chun1,2, LUAN Zhongjun1

(1.School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China；2. Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, Shanghai 200093, China)

In this study, we used a free vortex wake method based on a multi-lattice lifting surface to simulate aerodynamic performance at low and high wind speeds of the NREL Phase VI experimental two-blade horizontal axis wind turbine. To address the trailing edge separation lag caused by stall delay at high wind speeds, we coupled the Kirchhoff-Helmholz trailing edge separation prediction model and the Du-Selig 3D static stall delay model. We then calculated the aerodynamic performance at both low and high wind speeds for different yaw angle conditions. We also discuss the influence of different vortex lattice numbers on calculation accuracy. Our simulation results demonstrate that, at low wind speeds, the vortex lattice number has little influence, while it has great impact at high wind speeds. We obtained the best simulation results of the normal force and tangent force coefficients for the set of two vortex lattices on the lifting surface.

horizontal-axis wind turbine; multi vortex lattice lifting surface; free wake method; number of vortex lattices; yaw; stall delay; trailing edge separation

2015-06-12.網絡出版日期：2016-06-24.

國家自然科學基金項目(E51176129)；上海市科學技術委員會項目資助(13DZ2260900)；教育部高等學校博士學科點專項科研基金(博導類)項目(20123120110008).

王淵博(1991-)，男，碩士研究生;

李春(1963-)，男，教授，博士生導師.

王淵博，E-mail:shlgwyb@163.com.

10.11990/jheu.201506038

TK83

A

1006-7043(2016)08-1070-06