基于MATLAB的整體式轉向梯形優(yōu)化設計

喻超，王保華（湖北汽車工業(yè)學院，湖北 十堰 442002）

?

基于MATLAB的整體式轉向梯形優(yōu)化設計

喻超，王保華
（湖北汽車工業(yè)學院，湖北 十堰 442002）

以整體式轉向梯形機構的平面模型為基礎，建立了以實際外輪轉角與理想轉角偏差均方根為最小的目標函數(shù)。首先根據(jù)圖解法對整體式轉向梯形機構進行了初步分析，然后基于MATLAB優(yōu)化工具箱，對整體式轉向梯形機構進行優(yōu)化設計，與圖解分析結果進行對比，驗證了優(yōu)化結果的正確性。最后基于MATLAB/GUI設計了可視化的交互界面，簡化了整體式轉向梯形的優(yōu)化計算。

整體式轉向梯形；優(yōu)化設計；MATLAB/GUI

10.16638/j.cnki.1671-7988.2016.08.046

CLC NO.: U463.45Document Code: AArticle ID: 1671-7988(2016)08-141-04

為了減小行駛阻力和輪胎磨損，理想的轉向傳動機構應使車輛在轉彎過程中各車輪處于純滾動而無側滑的狀態(tài)，即在設計轉向梯形時，希望汽車內(nèi)外輪轉角完全符合Ackerman轉向原理[1]，但是由于轉向梯形機構自身的限制，其實際轉角與 Ackerman理想轉角之間存在一定的偏差。目前對整體式轉向梯形機構的優(yōu)化設計，大多是建立某一目標函數(shù)，根據(jù)各種約束條件得到最優(yōu)解[2～4]，但求解非線性優(yōu)化問題時，優(yōu)化結果與初始條件及約束條件有關，導致優(yōu)化結果各異且得不到驗證。本文首先根據(jù)圖解法得到某整體式轉向梯形機構[5]不同梯形臂長及梯形底角下的實際與理論左右轉向輪轉角關系曲線，然后提出了一種以實際外輪轉角與理想轉角偏差均方根為最小的目標函數(shù)，通過對轉向梯形機構的優(yōu)化，使其能夠最大限度的接近理想轉向梯形機構。優(yōu)化結果與圖解結果進行比對，驗證了優(yōu)化結果的正確性，并基于 MAT LAB/GUI，設計了可視化交互界面，能夠避免大量的重復性計算，直接得到優(yōu)化結果，對工程實際具有一定的借鑒作用。

1、整體式轉向梯形機構數(shù)學建模

1.1理想轉角關系的確定

汽車在轉向行駛時，受輪胎側偏角的影響，轉向中心點不在后軸延長線，而是位于前軸與后軸的某一點，由于影響輪胎側偏角的因素很多，此點位置難以確定。為了便于計算，忽略車輪定位參數(shù)的影響，假設車輪為剛性體，且轉向梯形機構為平面機構。

假設左轉為正。若要保證全部車輪繞一個轉向中心行駛，則梯形機構應保證內(nèi)、外車輪轉角滿足（如圖1所示）：

其中δi、δo分別為內(nèi)外輪轉角，k為兩主銷中心線延長線到地面交點之間的距離，l為汽車軸距。由式（1）可得同一軸理想的內(nèi)外輪轉角關系為：

1.2整體式轉向梯形數(shù)學建模

轉向梯形機構一般分為兩種：整體式轉向梯形與斷開式轉向梯形機構，而對于轉向橋采用非獨立懸架的汽車，一般采用整體式轉向梯形。當軸距一定時，內(nèi)外輪轉角的關系主要由梯形底角γ及梯形臂長d的設計決定，所以在設計時一般選取這兩個關鍵參數(shù)進行優(yōu)化。當車輪轉動時，內(nèi)、外車輪轉角與梯形底角及梯形臂長的關系如圖2所示。

根據(jù)三角函數(shù)關系

可得同一軸實際的內(nèi)外車輪轉角關系如下：

2、初步分析

對于某型號的汽車，其轉向機構的基本參數(shù)如下：k=2030mm，1=5000mm。在設計轉向梯形機構時，梯形底角γ及梯形臂長d過大，將使梯形機構的空間布置困難；γ及d過小時，轉向橫拉桿上的轉向力過大，容易使其發(fā)生變形，影響轉向精度。轉向梯形機構的優(yōu)化意味著在滿足約束條件的情況下，要使實際的內(nèi)、外輪轉角關系盡可能的接近阿克曼理論轉向。這里假設滿足阿克曼運動學條件就是理想的轉向系統(tǒng)，那么可以首先通過圖解法比較所設計的轉向梯形與理想的轉向梯形之間的關系，來評價設計的優(yōu)劣。

通過對相同梯形臂長，不同梯形底角的轉向梯形機構的分析（如圖3所示）， 可以看出：在相同的內(nèi)輪轉角下，隨著梯形底角的增大，實際的內(nèi)外輪轉角關系曲線逐漸偏離Ackerman理想轉角關系。當內(nèi)輪轉角在 10°范圍以內(nèi)時，曲線重合度較好；當內(nèi)轉向輪大于10°后，當梯形底角γ略大于70°時曲線與Ackerman理想曲線重合度最好。不同的梯形底角γ對內(nèi)外輪轉角關系影響較大。

當梯形轉向機構的梯形底角相同，取不同的梯形臂長值時（如圖4所示），可以看出，梯形臂長對內(nèi)外輪轉向關系影響較小，但是誤差值Δδo與梯形臂長成正比變化。

由上圖我們得到如下結論：梯形底角的變化對內(nèi)外輪轉角之間的關系有較大影響，梯形臂長的變化則影響梯形轉向機構的空間布置，進而影響汽車轉向性能的改變。

3、建立目標函數(shù)

3.1整體式轉向梯形數(shù)學建模

對于梯形轉向機構的優(yōu)化設計問題，其實是一個小型約束非線性規(guī)劃問題，可以通過調用 MATLAB（2014a）優(yōu)化工具箱中的fmincon函數(shù)來求解這個問題。

由于式（6）中的δDO及δAO為連續(xù)變量，對于所設計的梯形轉向機構而言，不能明確定義目標函數(shù)。因此，可以將式（6）改寫為在轉向梯形機構一般工作范圍-30°≤δi≤30°內(nèi)的偏差函數(shù)：

通過對一系列δi的計算分析，我們可以得出偏差e的變化趨勢。如果可以得到e的最小值，那么就可以找到相應的最優(yōu)解，另外，也可以通過分析e的變化趨勢來得到尋找最優(yōu)解的方向。

3.2約束條件

其中δmaxo為最大外輪轉角。

3.3優(yōu)化結果分析

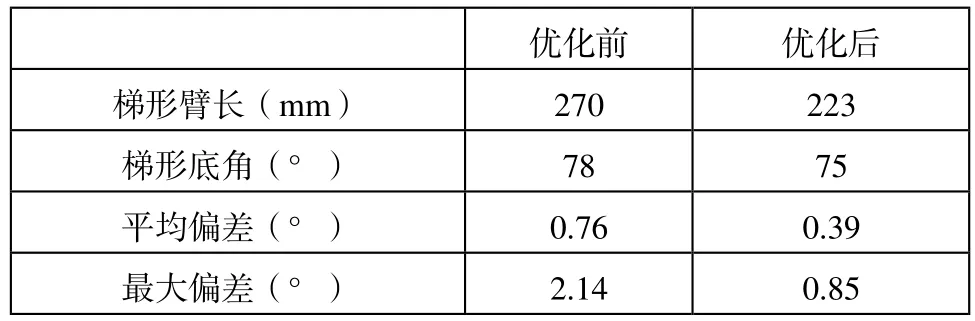
表1　某汽車轉向梯形機構優(yōu)化結果

從表1可以看出，經(jīng)過目標函數(shù)的優(yōu)化，在整個轉向梯形工作范圍內(nèi)，實際的外輪轉角與 Ackerman理論外輪轉角之間的平均偏差減小了0.4°左右，最大偏差值減小了1.3°。為了防止優(yōu)化后的局部最優(yōu)解，將優(yōu)化值與圖3、圖4的初步分析結果相對比，證實了優(yōu)化結果與圖解法相吻合，證明了優(yōu)化程序的正確性。優(yōu)化結果比較理想，可以有效提高轉向精度，改善輪胎的磨損。

4、GUI界面設計

為了更加直觀便捷地體現(xiàn)實際的內(nèi)外輪轉角與Ackerman理論轉角之間的變化關系以及優(yōu)化效果，基于MATLAB/GUI，設計了一個可視化的交互界面。GUI是指由窗口、菜單、按鍵、光標、圖標、對話框及文本框等各種圖形對象組成的用戶界面，它讓用戶定制用戶與MATLAB的交互方式。在此界面下，用戶通過輸入汽車基本參數(shù)如兩主銷中心距、汽車軸距以及允許的最大內(nèi)輪轉角，以及待優(yōu)化的轉向梯形機構梯形底角及梯形臂長的初始值，通過點擊優(yōu)化按鈕可以直接得到優(yōu)化后的結果，并可以輸出優(yōu)化前后內(nèi)外輪轉角與 Ackerman理論值之間的關系曲線以及優(yōu)化后的外輪偏差曲線，如圖5所示。

5、結語

本文通過對某汽車轉向梯形機構的初步圖解分析，以及MATLAB優(yōu)化工具箱進行優(yōu)化，得到了能夠最大程度接近Ackerman理想轉角關系的轉向梯形機構，兩者相互印證，保證了優(yōu)化結果的正確性。并基于MATLAB/GUI，設計了人機交互的可視化界面，通過簡單的參數(shù)輸入，即可得到最優(yōu)值，且能直觀地了解實際梯形轉向機構的內(nèi)外輪轉角與理想轉角之間的關系，對工程實踐具有一定的指導作用。

[1]Simionescu,P.A，Beale,D.Optimum synthesis of the four-bar generator in its symmetric embodiment:the Ackermann steering linkage[J].Mechanism and Machine Theory，2002，37(12)：1487-1504.

[2]劉旋，李騰飛，鄭帥廣.汽車整體式轉向梯形機構優(yōu)化設計[J].汽車實用技術,2014,3：28-30.

[3]王計廣，邢號彬，常秀巖，等.基于MATLAB優(yōu)化工具箱的整體式轉向梯形優(yōu)化設計[J].汽車零部件，2010,10:60-62.

[4]何正強，石凱凱.整體式轉向梯形機構的優(yōu)化設計[J].現(xiàn)代機械，2012,2:33-35.

[5]Reza N.Jazar.Vehicle dynamics:theory and application[M].Phoenix Lieb press,2008.

[6]羅永革，馮櫻.汽車設計[M].北京：機械工業(yè)出版社，2011.

Optimization Design Based on MATLAB for Integral Steering Trapezoidal Mechanism

Yu Chao,Wang Baohua
(Hubei University of Automotive Technology,Hubei Shiyan 442002)

Based on the plane model of integral steering trapezoidal mechanism,an optimum math model of objective functions which is minimum error of root mean square between practical and ideal outer corner angle was established.Firstly,according to the graphic method,the integral steering mechanism was analyzed,and based on the MATLAB optimization design of the integral steering trapezoid mechanism was carried out to verify the correctness of the optimization results.Finally,the interactive interface was designed based on MATLAB/GUI,which simplifies the optimization calculation.

integral steering trapezoidal mechanism; optimization design; MATLAB/GUI

U463.45

A

1671-7988（2016）08-141-04

喻超（1991-），男，碩士研究生，就讀于湖北汽車工業(yè)學院，從事傳動與控制方面的研究。

湖北省自然科學基金（2015BAA046）。