善于提問：基于習題教學的視角

☉江蘇省張家港市護漕港中學陳桂芬

善于提問：基于習題教學的視角

☉江蘇省張家港市護漕港中學陳桂芬

華東師大鐘啟泉教授在《“教會提問”的教學》一文中指出：“‘提問’的特征是懂得的人（教師）問不懂得的人（兒童）.這跟日常不懂得的人向懂得的人的發問，形成了鮮明的對照.正因為如此，在提問之際，必須明確地意識到為什么而問.”根據上述觀點，我們思考了習題教學中的提問角度，本文就基于日本教育心理學家佐伯胖歸納的教育現場的經驗，結合近年來習題教學的案例，解讀提問視角與反思教學立意，與同行研討.

一、促進深思的提問案例與意圖解讀

（一）改變視點的提問

題例1：如圖1，∠MON內有一點A.

（1）過點A畫AB∥ON交OM于B，畫AC∥OM交ON于C；

（2）過點M畫MH⊥ON，垂足為H；

（3）在上面畫圖的基礎上，度量、比較（用“=”“＞”“＜”填空）：∠MON_______∠BAC；OB______AH.

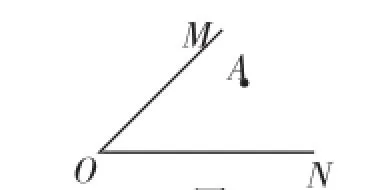
圖1

預設追問：如圖2，直線BE、CD相交于點A，且CD∥OB，AB∥ON.

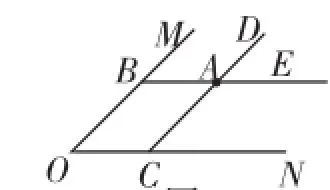
圖2

追問1：若∠MON=45°，求∠ACN的度數；

追問2：若∠DAE=45°，求∠MON的度數；

追問3：像（2）中的∠BOC、∠BAC稱為四邊形ABOC的一組“對角”，則該四邊形的另一組對角相等嗎？說明理由.

追問4：小睿同學提出一個命題：如果一個角的兩邊與另一個角的兩邊分別平行，那么這兩個角一定相等.請直接判斷這個命題是真命題還是假命題.

設計意圖：初看后續4個追問，貌似與前面的題例沒有關聯，其實在前面題例畫圖的基礎上，已經得到如圖2所示的圖形，所以我們的“追問”實際上是圍繞學生已畫出的圖形展開提問，也即改變視點的提問，把學生對這個圖形的認識引導到平行線的性質與判定的研究上來，并且在最后一問設計了一道判斷真假命題的較難問題，然而答案又恰恰在圖2中，因為在圖2中既能找到正例，也能找到反例.

（二）引進別的假定的提問

題例2：請結合夏新同學的收支情況表，思考下面的問題：

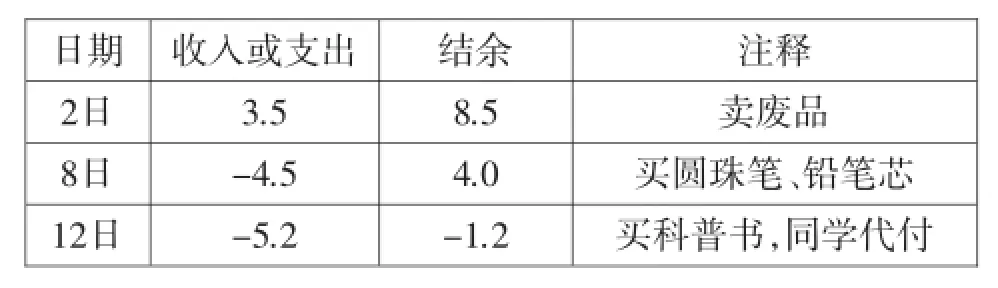
收支情況表

這是教材上容易找到的一個生活情境，我們在課前預設了如下的一些問題.

問題1：請將表格中第2、3列的6個數據分成兩個集合，注明分類依據；

問題2：從表格中可發現算式：8.5-4.5=4.0，類似地，請再寫出一個算式：________________；

問題3：小敏同學經過思考，發現了夏新同學在2日之前的零花錢數，你知道她是怎么想的嗎？

在學生成功解答上述問題之后，我們再引入目前較為流行的一種“新定義考題”，如問題4.

問題4：給出定義：給出兩個數a、b（a＞b），當a-b≤1時，稱（a，b）為“相鄰數對”，a-b為“相鄰數差”.如上面表格中的（4.0，3.5）就是“相鄰數對”，此時“相鄰數差”為0.5.

請寫出表格中另外的“相鄰數對”及“相鄰數差”.

設計意圖：針對一個生活現實，追求設問的角度多樣化.從本質上說，就是倡導開放式數學教學，把學生的思考引向“四面八方”.

（三）舉出例子的提問

題例3：在數軸上，點A、B分別對應著數a、b.

（1）①當a=2，b=6時，AB=_______；

②當a=-6，b=-2時，AB=_______；

③當a=____，b=_____時，AB=_______.（寫一組符合要求的即可）

（2）用含a、b的式子表示AB.

（3）式子|3-2|或|2-3|的圖形意義可以是：數軸上表示3、2的兩點之間的距離.

的圖形意義：_____________________；

|2+5|的圖形意義：_______________________.

設計意圖：初一學習數軸時，為了引導學生數形結合地分析問題，預設了上述問題，也是為了學生積累數軸上兩點之間距離公式而研制，同時還導引著后續平面直角坐標系中兩點距離公式的基礎.上面的（3）是結合數軸進行理解，其實我們還可通過恰當的設計，引導學生給出反例，比如在八年級學生學習了特殊等腰三角形性質之后，我們曾提出如下問題.

練習期間，小舟“發現”一個猜想：如果直角三角形中有兩邊之比為1∶2，則該直角三角形中必有一銳角為30°！請判斷小舟同學的“發現”命題的真假.如果是真命題，給出證明；如果是假命題，給出反例.

設計意圖：這個問題就是讓學生舉出反例，訓練學生的批判性思維.

（四）思考案例的提問

題例4：（1）求下列各數的算術平方根：①0.0025；②81；③32.

設計意圖：這是初學平方根后的一組運算練習，一般來說，新接觸一類數后，學習套路通常是這類新數的定義及相關概念，接著是這類數如何運算，所以這里安排一組化簡與簡單運算，就是遵循這樣的學習套路，在此基礎上，我們還可增加如下的追問.

追問：有同學在練習兩個無理數的運算后發現：兩個無理數相加（減），結果一定是無理數；而兩個無理數相乘，結果卻難確定.你怎么看這個同學的“發現”？建議舉例后再配文字闡述你的觀點.

追問意圖：通過這一追問，促進學生運算后的反思經驗，追求成果擴大，本質上是對實數運算是否封閉的深入思考.

（五）抽絲剝繭的提問

題例5：如圖3，△AOB中，A、B兩點的坐標分別為（2，4）、（6，2），求△AOB的面積.

圖3

（1）用兩種方法求三角形AOB的面積.

（2）小舟同學發現：過點B作y軸的垂線交AO于P，這時把三角形AOB分割成兩個三角形……也就能求出面積了！你能否完善這種思路？

設計意圖：這是學生初學平面直角坐標系后的一道習題，鼓勵學生從不同角度計算三角形面積之后，我們還可把設問視角“引向他處”，比如促進學生發現特殊圖形，追問如下.

追問：小杰經過度量發現，三角形AOB好像是個等腰直角三角形，……結合上面求出的面積就可以求出AO、BO的長……你能否完善這種思路.

追問意圖：學生雖然此時還沒有勾股定理的知識儲備，但是可以利用三角形面積與數的開方等知識來作出解釋，通過這一追問，抽絲剝繭，讓學生復習“一條主線”上的數學概念和性質.

（六）提示矛盾的提問

題例6：思考：x取哪些整數值時，2≤3x-7＜8成立？

（1）解不等式2≤3x-7；

設計意圖：這是一道基礎習題，初學不等式之后學生應該都能掌握，為了變換問題呈現的形式，多角度啟發學生思考，我們還預設了如下兩個追問.

追問1：小舟認為：不轉化為不等式組，也可以直接

解2≤3x-7＜8！你覺得小舟同學是怎樣解的？

小舟看到后，就指出小杰第一步就出錯了！……

你知道錯誤原因是什么嗎？請求出2x≤3x-7＜8的解集.

追問意圖：通過引入錯漏解法，讓學生參與辨析，學會診斷、糾錯與究錯，融錯于學習中.順便指出，還有一類應用問題本身由于記錄有誤，也是引發矛盾很好的題例，請看鏈接習題.

鏈接習題：【帳目閱讀】某家商店的帳目記錄顯示，某天賣出26支牙刷和14盒牙膏，收入264元；另一天，以同樣的價格賣出同樣的39支牙刷和21盒牙膏，收入393元.

【傾聽理解】該商店的會計人員稍加演算就發現上述記錄有誤！

【一起參與】請思考為什么上述記錄有誤.你能用二元一次方程組的知識來解釋嗎？

這個記錄是否有誤.如果有誤，請說明理由.

（七）提示發現的提問

題例7：如圖4，AD、BE、CF是△ABC的三條中線，若△ABC的周長是acm，當a=24時，求AE+CD+BF的值.

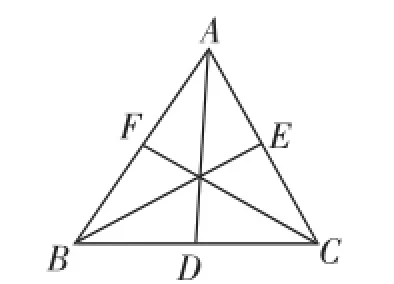
圖4

設計意圖：這是一道經典習題，利用中線性質，整體處理就可獲得解答.關鍵是我們增設了如下追問，促進學生發現問題、成果擴大.

追問1：小杰完成練習之后，發現CE+BD+AF的值也能求出，你會嗎？

追問3：設三條中線交于G點，小婧度量后發現：GE∶GB=GF∶GC=…，可是理由呢？你知道她發現什么了嗎？

追問意圖：這三個追問層層遞進，前兩問是從特殊到一般，最后一個追問更是隱含著三角形“重心定理”.

（八）變化條件的提問

題例8：如圖5，四邊形ABCD為矩形，過點D作對角線BD的垂線，交BC的延長線于點E，取BE的中點F，連接DF，DF=3.

（1）當F在BC的延長線上時，若AB=2，求矩形ABCD的面積.

（2）設AB=a，AD=b，請分析代數式a2+（b-3）2的值是否為定值？如果變化，說明理由；如果不變，求出這個定值.

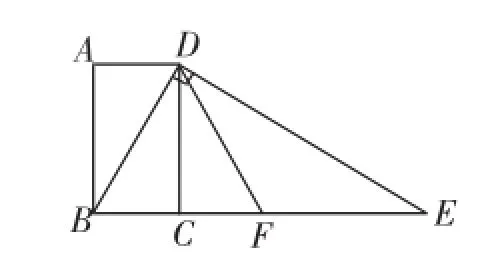
圖5

設計意圖：這是一次習題講評課上針對一道2015年中考題的變式講評，我們增設了（1），讓學生從常量計算過渡到變量最值的思考，并且在（1）限制了點F在BC的延長線上，避免了分類討論，事實上，對于優秀學生，我們還可跟進如下拓展思考.

拓展思考：若AB=1，畫圖分析矩形ABCD的周長.

這樣就需要分不同情形進行討論了，比如點F在邊BC上，或點F在BC的延長線上.通過這樣變化條件，從限制到開放，對學生縝密思維的考查就比較到位.

二、寫在最后

從本質上說，本文關注的其實是命題基本功，所謂“教會提問”“善于提問”，都需要教師在“三個理解”上持續修煉，不斷精進，既需要深入理解數學本質、數學基本思想，又需要理解學生，特別是不同學段學生的理解能力，還需要懂得教學，知道什么時候增加設問、追問是恰時恰點恰當的.當然，在這方面，知易行難，我們一起努力.

1.鐘啟泉.“教會提問”的教學［J］.基礎教育課程，2014（9）.

2.鮑建生，顧泠沅，等.變式教學研究［J］.數學教學，2003（1，2，3）.

3.鄭毓信.善于提問［J］.人民教育，2008（19）.

4.鄭毓信.善于優化［J］.人民教育，2008（20）.

5.劉東升.對時育物，有效追問——淺論初中數學課堂教學中的追問藝術［J］.中學數學教學參考（中），2012（4）.Z