新定義曲線問題的創(chuàng)新解答

☉湖南省長沙市周南中學　張璐瑤

新定義曲線問題的創(chuàng)新解答

☉湖南省長沙市周南中學張璐瑤

以新定義為背景的高考命題屢見不鮮，此類問題不僅能有效考查考生對基礎知識的掌握程度，而且對考生的創(chuàng)新能力和應用能力提出了更高的要求.解題此類問題時要徹底理清“新定義”的內(nèi)涵，結合相關知識加以靈活處理.下面以一類新定義曲線問題為例，就問題的創(chuàng)新解答進行分析.

一、題目展示

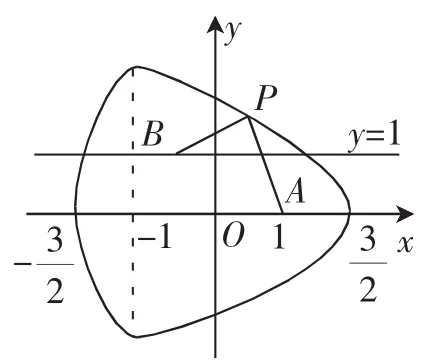
引例曲線C是平面內(nèi)與三個定點F1（-1，0），F(xiàn)2（1，0）和F3（0，，1）的距離的和等于的點的軌跡.給出下列四個結論：

①曲線C關于x軸、y軸均對稱；

②曲線C上存在一點P，使得|PF3|=

③若點P在曲線C上，則△FPF面積的最大值是1；

④△PF2F3面積的最大值為

其中所有真命題的序號是__________.

命題意圖：命題中定義一個新的概念，能有效考查學生即時學習的能力、培養(yǎng)學生的創(chuàng)新意識.對于解析幾何問題，可從數(shù)（方程）與形（曲線）兩個角度來認識事物，這兩種方式互為補充.

二、創(chuàng)新解答

1.把握新定義原理，直奔主題

新定義曲線是平面內(nèi)與三個定點的距離的和等于定值的點的軌跡，因此可直接設出動點坐標結合兩點間距離公式得出曲線方程.

設曲線C上任意一點坐標為P（x，y），由題意可知C的方程為

2.把握相關原理，間接判斷

對于①，判斷一個陌生曲線的對稱性問題，我們不易畫出曲線的圖像，所以利用對稱性的定義是首選策略.

在此方程中，用-x，-y分別取代x，y，可知C只關于y軸對稱，不關于x軸對稱.故①錯.

同理判斷一條曲線是否關于某條直線對稱，設直線為x=a，通過驗證f（2a-x）與f（x）的關系來實現(xiàn).

判斷某點是否為曲線的對稱中心，設點坐標為（a，b），可通過驗證F（2a-x，2b-y）與F（x，y）之間的關系來實現(xiàn).

3.把握問題本質(zhì)直接判斷

對于②，若|PF3|=，故②錯.

對于④，此時需要先考慮以F2，F(xiàn)3為焦點，實半軸為的橢圓E，其短軸頂點到直線F2F3：x+y-1=0的距離為.此時△PF2F3的面積為但是曲線C應該在此橢圓內(nèi)部，所以△PF2F3的面積應小于.故④正確.

三、變式演練

變式1曲線C是平面內(nèi)到定點A（1，0）的距離與到定直線x=-1的距離之和為3的動點P的軌跡，則曲線C與y軸交點的坐標是______；又已知點B（a，1）（a為常數(shù)），那么|PB|+|PA|的最小值d（a）=_______.

（2）由（1）可知y2=

如圖1所示，令y=1，則10x+ 15=1或-2x+3=1，解得x=-或1.

當-1＜a＜1時，直線y=1與y2=-2x+3于點P，滿足|PB|+|PA|取得最小值.所以此拋物線的準線為x=2，即直線y=1與準線的交點Q（2，1），此時d（a）= |QB|=2-a.

點評：本題以新定義曲線為背景綜合考查了拋物線的定義和性質(zhì)、直線與拋物線相交問題、兩點間距離公式等基礎知識與基本技能，考查了分類討論的思想及推理計算能力.

變式2曲線C是平面內(nèi)與定點F（2，0）和定直線x= -2的距離的積等于4的點的軌跡.給出下列四個結論：

①曲線C過坐標原點；

②曲線C關于x軸對稱；

③曲線C與y軸有3個交點；

其中，所有正確結論的序號是___________.

解析：設點P的坐標為（x，y）.因為曲線C是平面內(nèi)與定點F（2，0）和定直線x=-2的距離的積等于4的點的軌跡，所以因為當x=0時，y=0，故曲線C過坐標原點，故①正確.

令x=0時，y=0，故曲線C與y軸只有1個交點，故③不正確.

點評：解析幾何的本質(zhì)是用代數(shù)方法研究幾何性質(zhì)，為了研究曲線的性質(zhì)，首先要按定義求出曲線方程.再結合曲線的相關性質(zhì)及題目的隱含條件，即可順利求解.

變式3在平面直角坐標系中，動點P（x，y）到兩條坐標軸的距離之和等于它到點（1，1）的距離，記點P的軌跡為曲線W.

（Ⅰ）給出下列三個結論：

①曲線W關于原點對稱；

②曲線W關于直線y=x對稱；

③曲線W與x軸非負半軸，y軸非負半軸圍成的封閉圖形的面積小于，化簡得|xy|+x+y=1，用（-x，-y）代替方程中的（x，y）所得方程與原方程不相同，因此①錯誤.

把原方程中x，y互換，方程不變，因此曲線關于直線y=x對稱，故②正確.

其中，所有正確結論的序號是_____.

（Ⅱ）曲線W上的點到原點距離的最小值為______.

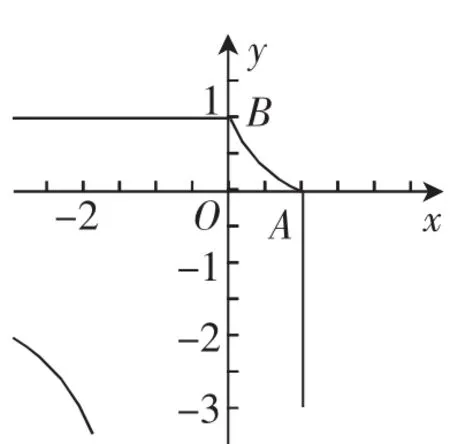
圖2　

點評：化生為熟是解決創(chuàng)新問題的基本策略，本題按定義求出曲線方程，再利用分類討論思想得出不同區(qū)間內(nèi)曲線的不同形狀，進而得出所求結論.