基于三次有理PH曲線的G2Hermite插值

馬淑娟,　唐　爍

(合肥工業大學 數學學院,安徽 合肥　230009)

?

基于三次有理PH曲線的G2Hermite插值

馬淑娟,唐爍

(合肥工業大學 數學學院,安徽 合肥230009)

文章在滿足G1Hermite插值條件的三次有理PH曲線的基礎上,通過簡單的方法構造了一個滿足G2Hermite插值條件的三次有理Bézier曲線。該方法只需根據始末端點的曲率來確定曲線的權重進而得到插值曲線,具有很好的幾何意義,數值實例表明了該算法的有效性。

有理PH曲線;Bézier曲線;G1Hermite插值;G2Hermite插值

已知端點數據的Hermite插值是計算機輔助幾何設計(computeraidedgemetricdesign,CAGD)中一種常用的構造曲線的方法。又因為有理Bézier曲線是系統中常用的一種模型,所以近年來，關于有理Bézier曲線的Hermite插值問題得到了研究[1-3]。

關于G2Hermite插值,文獻[4]提出了二階幾何平面三次Bézier曲線插值,通過求解二元二次方程組得到滿足插值條件的曲線表達式;文獻[5]拓展該方法提出了三次有理Bézier曲線,但該方法并未降低解的存在條件;文獻[6]通過增加自由度使曲線滿足G2插值條件;文獻[2]在三次有理Bézier曲線滿足G1Hermite插值條件的基礎上，增加2個自由度使其滿足G2Hermite插值條件,但是其端點處切向量與X軸夾角和不能超過2π/3,且解的存在性條件比較高;文獻[7]在G1Hermite插值基礎上,拓展成4個自由度,解的存在性條件依然比較高;文獻[8]提供了一種用2條二次有理曲線升階的方法來構造滿足G2Hermite插值條件的三次有理Bézier曲線,這種方法具有很好的幾何性質,但是因為引入交點b,限制了該曲線只能是C型,即曲線的控制多邊形只能是凸四邊形, 所以該方法不適用于構造S型曲線。

文獻[9]提出了有理PH曲線,并給出了該類曲線的統一表達式。有拐點的PH曲線次數至少為5。本文在文獻[3]的基礎上,利用PH曲線的復數表示給出滿足G1Hermite插值條件的三次有理PH曲線,并根據曲線始末端點的已知曲率來調節曲線權重，從而得到滿足G2Hermite條件的插值曲線,得到的插值曲線與三次有理PH曲線有相同的控制頂點，進而有相同的控制多邊形。該方法有很好的幾何性質，可廣泛應用于計算機數值控制與加工、離散插值計算、運動路徑控制等技術中。

1　預備知識

1.1三次有理PH曲線的G1Hermite插值

定義1平面上的有理參數曲線c(t)=(x(t),y(t))稱為有理PH曲線,是指存在有理函數R(t),使得[3]：

類似于多項式PH曲線,有理PH曲線也具有一些很好的性質,例如:有理PH曲線的等距曲線是有理曲線;有理PH曲線在正交和平移變換、等比例縮放以及分式線性參數變化下仍為有理PH曲線[10]。

定理1設

記(b0,T0;b3,T1)為G1Hermite插值條件，其中，b0、b3為始末端點坐標,T0、T1為相應的單位切向量,因為有理PH曲線在正交變換、平移變換及等比例縮放下仍為有理PH曲線，且分式線性參數變換不改變有理PH曲線的性質，所以可以假定w0=w3=1,此時,三次有理PH曲線可以寫成如下形式：

其中,t∈(0,1)，由定理1存在復系數多項式z(t)=z0(1-t)2+2z1(1-t)t+z2t2，滿足:

(1)

其中,z0=r0eiα；z1=r1eiθ；z2=r2eiβ，rj>0；α，β∈(-π/2,π/2);θ∈(-π,π)。

則由G1Hermite插值條件知2α、2β分別是已知兩端點切方向的輻角,即arg(T0)=2α,arg(T1)=2β。

1.2三次有理Bézier曲線表達式

根據文獻[12]，三次有理Bézier曲線可寫成如下形式：

若三次有理Bézier曲線控制多邊形如圖1a所示,則曲線為C型；若控制多邊形如圖1b所示,則曲線為S型。其中bi(i=0,1,2,3)為曲線控制頂點,曲率公式為:

(2)

始末端點的曲率只需分別令t=0,t=1,帶入(2)式可得:

(3)

圖1　曲線控制多邊形

2　三次有理Bézier曲線G2Hermite插值

構造G2Hermite插值曲線,實際上是尋找一個參數曲線,該曲線在滿足G1Hermite插值條件下,曲線始末2個端點還要滿足相應的曲率。

假設三次有理Bézier曲線g(t)的G2Hermite插值條件為(b0,T0,k0;b3,T1,k1),其中k0、k1為始末端點的曲率。由上述提到的三次有理Bézier曲線的表達式可知,只需確定曲線控制頂點及權重便可確定曲線,因此令滿足G2Hermite插值的三次有理Bézier曲線g(t)與滿足G1Hermite插值的三次有理PH曲線有相同的控制頂點,進而會有相同的控制多邊形。然后通過類似的方法[3],計算出權重w1、w2的值,使得三次有理Bézier曲線g(t)滿足G2Hermite插值。

下面首先給出一種構造滿足G1Hermite插值的三次有理PH曲線的方法。通過比較(1)式的系數,并由解的對稱性可得:

(4)

綜合以上3個方面可以得到如下的分類:

(1) 當z0z2=1時,有r0r2=1且α+β=0,此時,r0=r2=1,r1=|cosα|,θ=0,可以驗證插值曲線表示一段圓弧。

(3) 當z0z2≠1時,若r0r2≠0且α+β≠0,有如下情況:

當tanαtanβ≤0,且α+β<0,有

當tanαtanβ≤0,且α+β>0,有

C型三次有理PH曲線得以確定。

S型三次有理PH曲線得以確定。

其中,A=cos(α-β)+cos(α+β);

C=cos(α-β)-cos(α+β)。

根據不同的已知條件,滿足相應的關系可以得到θ的值,由α、β、θ的值可以算得r0、r1、r2的值,即

其中

由z0=r0eiα,z1=r1eiθ,z2=r2eiβ可以獲得曲線的控制頂點,因此滿足G1Hermite插值條件的曲線控制多邊形及表達式也隨之確定了。

以下討論在已知始末端點曲率的基礎上確定滿足G2Hermite插值條件的曲線權重。為了方便選擇與G1Hermite相同的坐標系,(3)式可以寫成如下形式:

(5)

其中

根據插值條件可知k(0)、k(1)為已知,C0、C1可由上述滿足G1Hermite插值的三次有理PH曲線得到,而w1′、w2′的計算公式為：

(5)

但是w1、w2的符號與曲線的類型有關系,若曲線為C型,則w1、w2同號;若曲線為S型,則w1、w2異號。因此有定理2。

定理2給定G2Hermite條件(b1,T0,k0;b3,T1,k1),β∈(-π/2,π/2),α∈(0,π/2,),若α、β滿足:

或滿足:

則存在唯一的三次有理Bézier曲線:

滿足G2Hermite條件,其控制多邊形與三次有理PH曲線相同。

下面給出三次有理Bézier曲線的G2Hermite插值算法。

輸入:G2Hermite插值條件(b1,T0,k0;b3,T1,k1)。

輸出:滿足插值條件的三次有理Bézier曲線。

算法步驟如下:

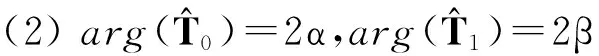
(3) 若α、β滿足α+β=0轉步驟(4),否則轉步驟(5)。

(5) 若tanαtanβ≤0且α+β<0,則有:

否則轉步驟(6)。

(6) 若tanαtanβ≤0且α+β>0,則有:

否則轉步驟(7)。

否則轉步驟(14)。

(8) 將α、β、θ的值帶入下式:

其中

(9) z0=r0eiα,z1=r1eiθ,z2=r2eiβ。

(12) 確定曲線權重為：

(13) 獲得G2Hermite插值曲線。

(14) 原插值條件無解。

3　數值實例

例1G2Hermite插值條件為:

b0=(-15.39,42.29),b3=(28.19,10.26),

該條件中α、β大小相同,因此滿足G1Hermite插值條件的三次有理PH曲線有2個解,一個解是圓弧，如圖2所示,另一個退化為多項式曲線，如圖3所示。

圖2　PH曲線為圓弧

圖3　PH曲線為多項式

圖中實線表示滿足G1Hermite插值條件的三次有理PH曲線,虛線表示滿足G2Hermite插值條件的三次有理Bézier曲線。

利用解的控制頂點,再由已知曲率值k0=0.5,k1=0.4便可得到滿足G2Hermite插值條件的三次有理Bézier曲線的權重,此時即可得到滿足插值條件的曲線表達式。

例2G2Hermite插值條件為:

b0=(-5.81,15.97),b3=(22.98,19.28),

根據已知條件可知α、β滿足tanαtanβ≤0,α+β<0,因此已知條件的插值曲線有解,代入數據可得到一條C型三次有理Bézier曲線如圖4所示。當k0=1,k1=0.2時本文方法與文獻[8]提出的方法得到的曲線做曲率對比如圖5所示。通過對比可以看出,用本文方法比用文獻[8]方法所得曲線的曲率變化明顯平緩很多。

圖4　α+β<0時，PH曲線為有理C型曲線

圖5　k0=1,k1=0.2時曲率對比

例3G2Hermite插值條件為:

b0=(-8.5,14.72),b3=(24.57,17.21),

根據已知條件可知α、β滿足tanαtanβ≤0,α+β>0，因此已知條件的插值曲線有解,代入已知數據可得到一條C型三次有理Bézier曲線如圖6所示。當k0=0.3,k1=0.2時本文方法與文獻[8]提出的方法得到的曲線做曲率對比如圖7所示。通過對比可以看出,用本文方法比用文獻[8]方法所得曲線的曲率變化明顯平緩很多。

圖6　α+β>0時，PH曲線為有理C型曲線

圖7　k0=0.3,k1=0.2時曲率對比

例4G2Hermite插值條件為:

b0=(-17.37,36.03)，b3=(26.53,27.21),

k0=0.005,k1=0.01。

由已知條件端點曲率k0、k1的值可知,欲求的插值曲線應為一條S型曲線,又因為α、β的值滿足上述所提到的S型曲線有解條件,故滿足此已知條件的三次有理Bézier曲線如圖8所示。

圖8　PH曲線為有理S型曲線

4　結　論

在滿足G1Hermite插值條件的三次PH曲線基礎上，本文構造了一個滿足G2Hermite插值條件三次有理Bézier曲線的簡單方法。在討論過程中可知，該方法可以將三次多項式PH曲線轉化成三次有理Bézier曲線,但此時的Bézier曲線只能為C型。因為Bézier曲線的控制頂點與PH曲線控制頂點一樣,所以它們的控制多邊形也一樣；但是曲線權重取決于始末端點處的具體曲率數值。這種方法能得到唯一且精確的解,并具有很好的幾何性質。

方法的不足之處在于構造PH曲線時初始條件受限制,可能會出現無解的情況。這時可以通過文獻[13]的方法插入滿足條件的中間數據來構造段數最少的PH樣條曲線的方法, 以達到G1插值的目的；然后再在每個節段用文獻[8]方法得到滿足G2插值的三次有理Bézier曲線。

[1]FARING.Curvesandsurfacesforcomputeraidedgeo-metricdesign[M].NewYork:AcademicPress,1996.

[2]FARING.GeometricHermiteinterpolationwithcircularprecision[J].Computer-AidedDesign,2008,40(4):476-479.

[3]潘俊.有理三次PH曲線的G1Hermite插值[J].復旦大學學報(自然科學版),2007,46(2):184-191.

[4]DEBOORC,HOLLINK,SABINM.HighaccuracygeometricHermiteinterpolation[J].ComputerAidedGeometricDesign,1987,4(4):269-278.

[5]DEGENWLF.Highaccuraterationalapproximationofparametriccurves[J].ComputerAidedGeometricDesign1993,10(3/4):293-313.

[6]SAKAIM.Osculatoryinterpolation[J].ComputerAidedGeometricDesign，2001,18(8):739-750.

[7]WALTONDJ,MEEKDS.G2Hermiteinterpolationwithcircularprecision[J].Computer-AidedDesign,2010,42(9):749-758.

[8]LIYajuan,DENGChongyang,MAWeiyin.C-shapedG2HermiteinterpolationbyrationalcubicBéziercurvewithconicprecision[J].ComputerAidedGeometricDesign,2014,31(5):25-8-264.

[9]POTTMANNH.Rationalcurvesandsurfacewithrationaloffsets[J].ComputerAidedGeometricDesign,1995,12(2):175-192.

[10]孫露露.關于PH曲線插值若干問題的研究[D].合肥:合肥工業大學,2010.

[11]FAROUKIRT,NEFFCA.Hermiteinterpolationbypythagoreanhodographquintics[J].MathematicsofComputation,1995,64(212):1589-1609.

[12]PIEGLL,TILLERW.TheNURBSbook[M].2nded.NewYork:Springer-Verlag,1997.

[13]馬元魁,張天平,康寶生.C1插值平面三次PH樣條的構造 [J].西安工業大學學報,2007,27(1):34-37,51.

(責任編輯張镅)

G2HermiteinterpolationbasedonrationalcubicPHcurve

MAShujuan,TANGShuo

(SchoolofMathematics,HefeiUniversityofTechnology,Hefei230009,China)

BasedontheG1HermiteinterpolationbyarationalcubicPythagorean-hodograph(PH)curve,asimplemethodforG2HermiteinterpolationbyarationalcubicBéziercurveispresented,whichhasawell-understoodgeometricalmeaning.Inthismethodtheweightsofthecurveareacquiredbythecurvaturesatboththestartingpointsandendpoints.Theeffectivenessofthealgorithmisverifiedbynumericalexamples.

rationalPythagorean-hodograph(PH)curve;Béziercurve;G1Hermiteinterpolation;G2Hermiteinterpolation

2015-03-27；

2015-06-06

國家自然科學基金資助項目(61272024)

馬淑娟(1990-),女,安徽宿州人,合肥工業大學碩士生；

唐爍(1964-),男,安徽巢湖人,合肥工業大學教授,碩士生導師.

10.3969/j.issn.1003-5060.2016.08.027

TP391.72

A

1003-5060(2016)08-1142-06