淺談初中數學的情境式概念教學

湯奎鋒

【摘 要】 數學概念的產生主要來源于現實生活和數學知識自身發展的結果，因此概念的引入通常是基于數學知識的現實原型或現實需要，或者是基于數學知識本身的邏輯結構，以舊引新。基于“數學現實”探究、建構概念，創設生活情境、趣味情境引入，進行具體的操作活動引入，聯想類比概念引入，創設矛盾沖突引入。數學概念引入階段的實施策略：典型性、適度性、有效性。

【關 鍵 詞】 初中數學；概念教學；創設情境；數學現實

中圖分類號：G633.6 文獻標識碼：A 文章編號：1671-0568（2016）12-0107-02

在設計教學情境時，除了讓學生親身感知問題，更需要的是促使學生展開積極思考、從實際情境中去發現數學知識。因此，情境設計的根本目的從“引趣”走向“引思”是非常必要的。數學概念的產生主要來源于現實生活和數學知識自身發展的結果，而概念的引入通常是基于數學知識的現實原型或現實需要，或者是基于數學知識本身的邏輯結構，以舊引新。

1. 基于“數學現實”探究、建構概念

教師要突出學生的“主體地位”，扮演好組織者、引導者與合作者的角色，更多地關注預設以外學生的“異想天開”，善于捕捉學生的智慧火花，鼓勵學生進行合情推理，訓練學生的直覺思維，通過啟發性的問題幫助學生形成概念。

形成一個概念，一般經歷從片面到全面、從模糊到清晰、從表象到本質的復雜思維過程。如果教師給學生充分思考的時間，學生個體對于情境或者問題會做出真實的、本能的第一反應，這種思維的結果和假設在教師引導下會逐步清晰化和理想化，最終形成概念。如果由教師代替學生快體驗、快抽象出數學概念，這種不連貫的學習活動，會造成學生建構的概念缺乏完整性。

[案例1]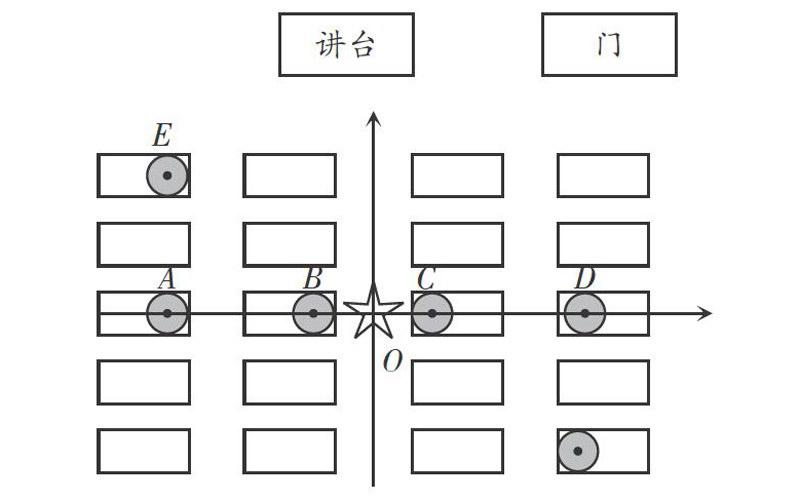

教師設問：觀察這5個數：300000、150000、653000、953700、453780，想想你有更簡單的表示方法嗎？

教師拋出問題，讓學生進行思考和交流后，學生提出了以下3種表示方法：

第一種：3×105、1.5×105、6.53×105、9.537×105、4.5378×105

第二種：3×105、15×104、653×103、9537×102、45378×101

第三種：0.3×106、0.15×106、0.653×106、0.9537×106、0.45378×106

教師引發學生對數學概念的思考以后，還需要用啟發性、探索性、層進性的問題去引發、驅動。教師可以用“你能得到什么”“你是怎樣得出來的”“你為什么要這樣做”等問題引發學生頓悟，從而成功建構概念。

[案例2]

為了啟發學生：同一直線上的點的描述需要考慮方向和大小，在腦海里聯想到數軸又從一維的直線過渡到二維平面上的點，從而設置兩條數軸（兩個方向），以此形成平面直角坐標系形式化的定義，設計下列問題：

（1）若老師站在教室第三排的走廊中間（圖中五角星O），先請4位同學（位于圖中圓點A、B、C、D的位置）說說如何描述自己的位置相對老師的位置。

（2）再請兩位同學（位于圖中的圓點E、F的位置）說說如何描述自己的位置相對老師的位置。

（3）回顧之前學過的有關數軸的內容——數軸的三要素以及數軸上的每一個點都對應著一個實數值，思考并交流如何表示平面上的一個點。

教師除了預設一些遞進的、有針對性的問題外，還要針對學生的回答給予及時回應，隨機應變地進行啟發和點撥，讓學生不斷地修正思考的方向，這對教師的臨場反應能力有一定的要求。

2. 創設生活情境引入——基于概念抽象的原型

雖然有些數學概念是高度抽象后形式化的產物，但在現實生活中仍能找到許多概念的原型。因此，教學中可以利用這些概念的生活原型來創設情境，喚起學生的興趣，讓學生借助自己的生活經歷，感受、體會數學概念的產生是科學發展和生產實踐等實際應用的需要。

[案例3]

在教授“平面直角坐標系”概念時，教師可以創設如下情境：

題1.當破譯小高手（如下表）

（1）請破譯下列密碼：

A5 B5 C4 E5 B1 C2（有志者事竟成）

（2）請編制密碼：

天才來自勤奮（B4 D2 E3 C5 D4 C3）

題2.做影院服務生

（1）你會在電影院找到電影票上所指的位置，對號入座嗎？

（2）在電影票上，“4排3號”與“3排4號”是同一個座位嗎？為什么？

3. 創設趣味情境引入——基于概念學習的動機

有時可以創設一些生動、有趣的材料來加強學習的刺激，“以趣引思”。在具體操作中，我們要注意趣味性材料一定要和概念的屬性相聯系，避免“一笑而過”的情況發生。

[案例4]

在教授“科學計數法”概念時，教師可引用以下幽默故事來吸引學生的興趣，并寓意大數的表示需要簡化表達，隱含科學計數法的必要性。

有一個傻小子跟先生學字，聽先生教過“一、二、三”后，心想原來寫字這樣簡單，就讓他父親把先生辭掉了。有一天，父親要請一位客人吃飯，讓傻小子寫一份請柬。可是，傻小子過了很長時間還沒有出來，父親便去問，卻見他在紙上畫橫杠。傻小子一見父親，便說：“你請誰不好，偏要請‘萬百千！”

4. 進行具體的操作活動引入——基于概念的感性積累

有些數學概念的引入可以通過設計一些實踐活動，讓學生在活動中體驗、感悟概念的內涵，從而積累感性認識，為概念的形成作鋪墊。例如，在“平移”的教學中，除了觀察生活中的平移現象外，可以讓學生嘗試用幾何畫板軟件移動電腦屏幕上的三角形。運用軟件中的軌跡跟蹤功能顯示頂點的運動軌跡，可以讓學生非常直觀地觀察移動的方向和移動的距離。

5. 聯想類比概念引入——基于數學概念間的聯系

在數學概念體系中，許多概念有相似的內容和結構，以及相似的研究方法。因此，在引入新概念時，通過與相關概念進行聯想類比，可以得到新概念與相關概念在認識及處理方法上的一些共通點或規律。例如，在引入分式概念時，可以和分數概念進行類比；在引入向量的運算時，可以與實數的運算作聯想類比。

6. 創設矛盾沖突引入——基于數學知識發展的需要

有些概念的產生源于數學自身知識結構的發展，如無理數等數學概念的引入是為了解決之前數學中的某些矛盾、某種問題或滿足某種需要。可通過創設問題情境，引起認知失調，激發解決問題的動機，從而引出新概念產生的必要性。

[案例5]

在學生充分展示了如何由兩個小正方形（邊長均為單位1）拼成一個大正方形后，教師設問：①大正方形面積是多少？（面積是2；若設邊長為a，則a2=2）②它的邊長是多少？是已學過的有理數嗎？為什么？③它是不是之前學過的整數或者分數？

通過探討a不是有理數，但又是客觀存在的，從而引出數系從有理數擴充到無理數的必要性。

7. 數學概念引入階段的實施策略

（1）典型性。創設的情境要具有一定的典型性，蘊含數學概念的現實背景或本質屬性。并不是所有的數學概念都一定要通過生活情境來引入，如果是“為了情境而情境”，往往會適得其反。

（2）適度性。在引入概念時，設計的問題或活動要符合學生的認知水平，處于學生思維的最近發展區，讓學生從心理上感到親切。其次，如果提供的感性材料數量過少，則學生的感性體驗不夠；如果感性材料過量又會讓學生產生乏味感，因此，要把握好情境的量，讓學生既能有充足的活動體驗，又不會產生“情境疲勞”。

（3）有效性。好的情境才能讓學生觸“境”生情，激發學習的興趣。創設的情境要避免虛假的情境，注意情境的合理性。另外，設置情境的目的不僅是感性認識的鋪墊，更要讓學生產生思考、發現問題。因此，在概念引入中，問題才是核心。

（編輯：胡 璐）