有限尺寸V型薄板功率流透射損失研究*

湯　冬, 龐福振,3, 王青山, 姚熊亮

(1.哈爾濱工程大學船舶工程學院，黑龍江 哈爾濱 150001； 2.哈爾濱工程大學機電工程學院， 黑龍江 哈爾濱150001；3.中國人民解放軍92857部隊, 北京 100007)

?

有限尺寸V型薄板功率流透射損失研究*

湯冬1, 龐福振1,3, 王青山2, 姚熊亮1

(1.哈爾濱工程大學船舶工程學院，黑龍江 哈爾濱 150001； 2.哈爾濱工程大學機電工程學院， 黑龍江 哈爾濱150001；3.中國人民解放軍92857部隊, 北京 100007)

基于薄板理論，采用回傳射線矩陣法研究了兩對邊簡支任意角連接有限尺寸V型薄板的功率流透射損失。引入對偶坐標系，在力作用點和板接縫處對結構進行離散，同時考慮彎曲波動與面內波動效應，根據結構連接處的位移協調條件、力平衡條件以及兩端邊界條件得到V型薄板結構的散射矩陣。根據對偶坐標系的內在物理關系得到整體相位矩陣，最后推導出結構的回轉射線矩陣。在此基礎上，建立了V型薄板結構的動態響應分析模型以及功率流分析模型，通過對簡諧點激勵力作用下結構的動態響應進行對比分析，證明回傳射線矩陣法具有很高的求解精度與求解效率。最后，分析了V型薄板結構功率流傳導問題，研究了不同角度、不同板厚和不同阻尼損耗因子的V型薄板的功率流透射損失變化規律。

結構動力分析； 功率流； 透射損失； V型薄板； 回傳射線矩陣法

引　言

薄板結構(板厚與短邊比小于0.05)由于其經濟性和適用性而在橋梁建筑、水利工程、航空航天、船舶與海洋和土木建筑等結構工程領域具有廣泛的工程應用背景。工程中很多主體結構都是由兩塊或多塊薄板連接而成，作用于結構上的振源激勵通過連接板結構向振源以外的其他區域傳遞，引起結構局部振動并向外輻射噪聲，嚴重影響結構的使用性能以及人員的正常工作，因此，研究結構振動在連接板結構中的傳遞特性具有重要意義。

薄板的振動問題是一個經典的結構動力學問題[1-4]，Kirchhoff[2]首先提出了一個完整的薄板振動理論，并得到廣泛認可。盡管后人在其基礎上提出了更為精確的板殼理論，但是，基于這些理論所建立的方程的求解難度也相應增加，然而，對于絕大部分涉及到薄板結構的工程技術問題，運用Kirchhoff薄板理論就可以得到足夠準確的結果。

目前，有關連接板結構的研究主要關注L型板的動響應與功率流傳遞問題[5-11]，而研究V型板結構動響應的文獻相對較少。Yuanming Lai等[12]用分段函數(Step Function)對V型板結構進行了動響應分析，并給出了該結構自由振動的頻率方程，與FEM計算結果一致。Amin Paykani等[13]利用有限元軟件ABAQUS分析了V型板結構在水雷爆炸載荷下的動響應。

雖然L型板在工程實際中具有廣泛的應用，但是，在諸如船體舷側外板與各層甲板連接處和船體底龍骨或底部縱桁與船體外板連接處的很多地方會涉及到V型板。由于連接角度的不同，V型薄板面內波與面外波在板接縫處的耦合關系與L型板存在差異，研究V型薄板功率流透射損失能將連接板結構的動力性能研究推向更一般的情況，從而具有重要意義。

對于任意角連接的V型薄板結構，理論求解十分困難。常用的數值方法有有限元法(FEM)，邊界元法(BEM)和統計能量法(SEA)等，其中，FEM在工程實踐中有著最為廣泛的應用。除了上述數值方法以外，傳遞矩陣法(MTM)[14]是求解連接結構最有效的方法之一，針對MTM數值不穩定的缺點，Howard和鮑亦興[15]提出了一種改進的MTM——回傳射線矩陣法(MRRM)。

FEM的特點是單元離散化，計算結果近似性和適用范圍寬廣，然而，不能直觀反映結構內部的物理現象。與FEM的近似性不同，MRRM是一個具有鮮明物理意義的半解析半數值方法。首先，MRRM基于結構動力學方程得到結構響應的波動解；其次，通過在結構構件兩端建立對偶坐標系，一方面避免在矩陣中出現大指數項，保證了數值計算的穩定性，另一方面將結構中的波分為入射波和出射波(到達波和離開波)，從而賦予結構中波動響應明確的物理意義；再者，MRRM采用矩陣列式和矩陣運算，具有列式統一，便于推廣應用的特點；最后，MRRM通過Fourier變換計算結構的頻域響應，在Fourier逆變換中運用Neumann級數展開代替矩陣求逆，消除了矩陣奇異性的影響，可以精確計算短時瞬態波在結構中的傳播[16]。近年來，MRRM在結構動力分析領域得到廣泛應用[17-19]。

本文基于Kirchhoff薄板理論，采用MRRM研究了兩對邊簡支任意角連接的有限尺寸V型薄板功率流透射損失。首先，用波動法求解兩對邊簡支的Kirchhoff薄板運動微分方程，并將方程的解表示成矩陣的形式，得到薄板位移狀態向量和力狀態向量與到達波幅值向量和離開波幅值向量之間的關系。然后，將V型薄板在激勵力作用點和板接縫處進行離散，形成3塊板和4條節線，并在各節線處建立對偶坐標系，通過節線處的位移連續和力平衡條件得到各節線處的散射矩陣，并組裝得到總體散射矩陣，通過總體到達波幅值向量和離開波幅值向量的關系得到總體相位變換矩陣和置換矩陣，由此得到回傳射線矩陣。結合邊界條件求出總體到達波幅值向量和離開波幅值向量，代入位移狀態向量和力狀態向量的表達式中得到V型薄板的動響應，并以此計算V型薄板功率流及透射損失。最后，本文以兩對邊簡支，另外兩對邊自由的V型薄板為例，研究了不同角度、不同板厚和不同阻尼損耗因子的V型薄板的功率流透射損失變化規律。

1　理論推導

1.1V型薄板受力分析

V型薄板是由兩塊薄板在板接縫處以角度θ連接而成，如圖1(a)所示。在板中任取一個微元，其面內和面外受力分析分別如圖1(b)和(c)所示。

圖1　V型薄板幾何模型和受力分析圖Fig.1　Schematic diagram of the geometry and internal forces of the V-shaped thin plate

根據薄板單元受力平衡和廣義Hooke定律以及薄板單元的應變位移關系可以得到作用在以x軸方向為法向的平面上薄板內力和薄板面外位移w、面內縱向位移u和面內切向位移v之間的關系如下[8, 20]：

(1)

(2)

(3)

(4)

(5)

(6)

式中E為薄板材料彈性模量，μ為泊松比，h為薄板厚度，D=Eh3/[12(1-μ2)]為薄板彎曲剛度；w為薄板面外位移，u為薄板面內縱向(沿x軸方向)位移，v為薄板面內切向(沿y軸方向)位移；Qx為由彎曲作用產生的沿薄板平面法向的剪力，Nxx和Nxy分別為薄板面內沿x軸方向的正應力的合力和沿y軸方向的剪應力的合力，Mx為薄板所受的繞y軸的彎矩，Mxy為薄板所受的繞x軸的扭矩，Vx為由彎曲和扭轉作用產生的沿薄板平面法向的總剪力。

1.2薄板運動微分方程及其解

根據薄板單元的受力分析和廣義Hooke定律以及薄板單元的應變位移關系可以得到薄板面外運動、面內縱向運動和面內剪切運動微分方程分別為[21]：

(7)

(8)

(9)

對于受到簡諧激勵的兩對邊簡支板，上述面內和面外位移方程的解可以表示成y軸方向固有模態與x軸方向行波解的乘積形式[20, 21]：

(10)

(11)

(12)

將式(10)分別對x和y求偏導，得到薄板剖面繞y軸和x軸的轉角φx和φy，其表達式為：

(13)

(14)

若不考慮簡諧時間因子eiωt，由式(10)～(13)可以將位移狀態向量表示成矩陣形式

(15)

將式(10)～(12)代入式(2)～(4)和(6)可以得到Nxx，Nxy，Mx和Vx的表達式：

(19)

同理，若不考慮簡諧時間因子eiωt，由式(16)～(19)可以將內力狀態向量表示成矩陣形式

(20)

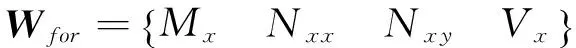
1.3MRRM求解任意角V型薄板

受簡諧點激勵作用以角度θ連接的兩對邊簡支V型薄板如圖2所示。

圖2　V型薄板幾何模型Fig.2　Geometry model of the V-shaped thin plate

在對V型薄板進行動力響應分析時，將V型薄板在板接縫處分成兩塊薄板，分別對兩塊薄板進行受力分析，通過板接縫處的位移連續條件和力平衡關系確定兩塊薄板的動力耦合關系。按照回傳射線矩陣法的思想[16]，在V型薄板板接縫處和激勵力作用點處進行離散，將V型薄板分成3塊板，形成4條節線，如圖3所示。

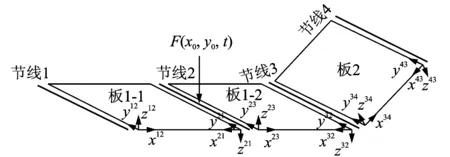
圖3　V型薄板離散圖及其對偶坐標系Fig.3　Discrete model and a dual local coordinate system of the V-shaped thin plate

1.3.1散射矩陣

對于節線3，由位移連續條件可以得到如下關系：

(21)

(22)

(23)

(24)

由式(21)～(24)可知，對于任意階模態m都有

(25)

即

(26)

由力平衡條件可以得到如下關系：

(27)

(28)

(29)

(30)

由式(27)～(30)可知，對于任意階模態m都有

(31)

即

(32)

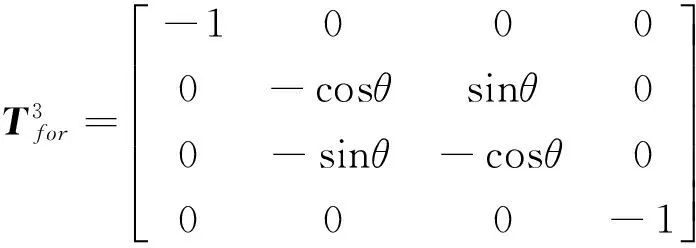
式(25)和(32)可以表示為

d3=S3a3

(33)

式中d3，a3和S3分別為節線3處的離開波幅值向量、到達波幅值向量和散射矩陣，其表達式為：

對于節線2，由位移連續條件可以得到如下關系：

(34)

(35)

(36)

(37)

由式(34)～(37)可知，對于任意階模態m都有

(38)

即

(39)

由力平衡條件可以得到如下關系：

(40)

(41)

(42)

(43)

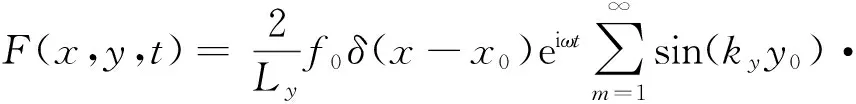
sin(kyy)，其中ky=mπ/Ly。

由式(40)～(43)可知，對于任意階模態m都有

(44)

即

(45)

式(39)和(45)可以表示為

d2=S2a2+s2

(46)

式中d2，a2，S2和s2分別為節線2處離開波幅值向量、到達波幅值向量、散射矩陣和波源向量，其表達式為：

下面討論V型薄板在節線1和節線4處的邊界條件。

若V型薄板在節線1和節線4處為無限長，則節線1和節線4處為無反射邊界條件。對于局部坐標系(oxyz)12，板1-1中只有沿x12軸負向傳播的波，對于局部坐標系(oxyz)21，板1-1中只有沿x21軸正向傳播的波；對于局部坐標系(oxyz)43，板3中只有沿x43軸負向傳播的波，對于局部坐標系(oxyz)34，板3中只有沿x34軸正向傳播的波。即

(47)

(48)

若V型薄板在節線1和節線4處為自由邊界，則有

(49)

即

(50)

若V型薄板在節線1和節線4處為剛性固定邊界，則有

(51)

即

(52)

若V型薄板在節線1和節線4處為簡支邊界，利用回傳射線矩陣法也可以求解，只是需要將位移狀態向量和力狀態向量進行重新組裝，本文將不考慮這種邊界條件。

通過上述分析得到了節線1～4處的局部散射矩陣S1,S2,S3和S4，現將局部散射矩陣組裝成總體散射矩陣。

結合式(33),(46)和(50)或(52)，V型薄板結構的總體散射關系為

dz=Szaz+sz

(53)

式中dz，az，Sz和sz分別為總體離開波幅值向量、總體到達波幅值向量、總體散射矩陣和總體波源向量，其表達式為：

1．3．2相位矩陣和置換矩陣

在任意一塊板中的同一個波，既是左(右)節線的離開波，也是右(左)節線的到達波，兩者的振幅相等而相位不同。在板1-1中，離開波與到達波幅值相位滿足如下關系：

(54)

(55)

(56)

(57)

(58)

(59)

(60)

(61)

式(54)～(57)和式(58)～(61)可以分別表示成：

(62)

(63)

式中L12為節線1和節線2之間的距離;a12，d12，a21和d21分別為節線1和節線2處的到達波和離開波幅值向量;P(x)為節線處離開波與到達波幅值向量的相位變換矩陣，其表達式為：

同理可知板1-2中離開波與到達波幅值向量的相位滿足如下關系：

(64)

(65)

板2中離開波與到達波幅值相位滿足如下關系：

(66)

(67)

由此可得離開波與到達波幅值的總體相位滿足如下關系

(68)

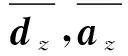
(69)

結合方程(68)和(69)可得

az=PUdz

(70)

聯立方程(53)和(70)可得

(I-SPU)dz=sz

(71)

式中R=SPU為V型薄板結構回傳射線矩陣。

由方程(71)可以求出整體到達波幅值向量

(72)

結合式(70)和(72)可以求出整體離開波幅值向量

(73)

將整體離開波幅值向量和整體到達波幅值向量代入前面所述的位移狀態向量和內力狀態向量中，即可求出V型薄板任意位置處的位移和內力。

2　數值計算

2．1模態截斷數的確定

為了保證求解結果的收斂性和準確性，需要確定計算過程中所需的模態截斷數，從而需要研究不同頻率范圍內V型薄板的模態密度。研究表明：V型薄板的模態密度近似等于每塊薄板的模態密度之和[22]，而在低于給定頻率ω的范圍內，平板彎曲振動的模態數為[23]

(74)

式中kB=(ω2ρh/D)1/4為平板彎曲波數，S為平板表面積。由式(74)可知板中彎曲波、縱波和剪切波收斂所需模態截斷數分別為[8]：

(75)

(76)

(77)

2．2回傳射線矩陣法(MRRM)和有限元法(FEM)計算結果對比

對于鋼質V型薄板，其材料屬性和幾何參數如表1所示。

表1　V型薄板材料屬性和幾何參數

其中，在分析阻尼損耗因子的影響以外的其他情況，阻尼損耗因子均取值η=0。

在板1中心點作用單位簡諧力，分別用MRRM和FEM計算θ分別為π/3，π/2和π時V型薄板的動響應，將上述兩種方法計算得到的板1中心點和板2中心點位移響應進行對比，如圖4所示。

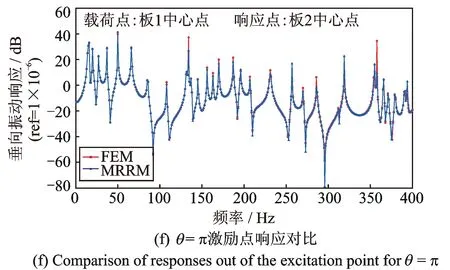
圖4　有限元法(FEM)和回傳射線矩陣法(MRRM)計算結果對比Fig.4　Comparison of the calculation results from FEM and MRRM

圖4中(a)和(b)，(c)和(d)以及(e)和(f)分別給出了θ=π/3，θ=π/2和θ=π時用有限元軟件ANSYS(14.5版本)和MEEM計算在板1中心點受單位簡諧力激勵的無阻尼V型薄板板1和板2中心點的垂向位移響應。從圖中可以看出，回傳射線矩陣法(MEEM)計算V型薄板在簡諧點激勵下的計算結果與有限元法(FEM)的計算結果非常吻合。因此，本文所采用的MEEM求解結構動力響應問題具有較高的計算精度。

同時，針對同一V型薄板參數(如表1所示)，采用MRRM和FEM求解時間分別列于表2。

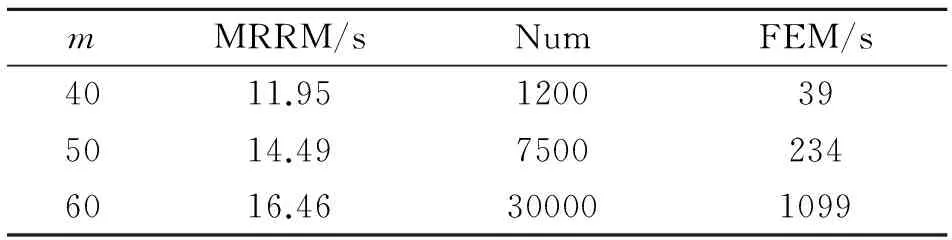
表2　MRRM和FEM計算時間對比

其中,m是y軸方向的模態數，Num是指網格單元數量。

通過表2的對比可以發現，MRRM求解V型薄板結構響應所耗時間明顯小于FEM計算耗時。此外，MRRM計算耗時對y軸方向的模態數變化不敏感，而FEM計算耗時對網格單元數量的變化較為敏感。

2．3V型薄板中功率流透射損失的計算

當外界激振力隨時間以簡諧規律變化時，V型薄板中功率沿板長度方向上的分布為[8,24-26]

(78)

式中符號*表示復數取共軛，Re表示復數取實部。

本文通過計算板1距離板接縫0.5 m(即x32=0.5)處的入射功率P1和板2距離板接縫0.5m(即x34=0.5)處的透射功率P2，得到V型薄板接縫處的功率流透射損失(TL)

TL=10lg(P1/P2)

(79)

V型薄板接縫處的功率流透射損失表征了板接縫對V型薄板中功率傳導效率的影響。

2.3.1無限長V型薄板功率流透射損失

圖5(a)表明，不同角度無限長V型薄板功率流透射損失的差異隨著頻率的增加而增大，當頻率低于150Hz時，不同角度無限長V型薄板功率流透射損失的峰值和谷值所對應的頻率是一致的，而當頻率高于150Hz時，不同角度無限長V型薄板功率流透射損失的峰值和谷值所對應的頻率有所不同。這是因為在低頻范圍內，面內波影響有限，V型薄板中功率流透射損失主要以面外波為主；隨著頻率的升高，薄板中波長減小，V型薄板連接處面內波與面外波的耦合效果增大，從而導致透射損失峰谷值產生偏移。

圖5　不同角度無限長V型薄板功率流透射損失Fig.5　TL of power flow through an infinite V-shaped plate coupled with various angles

當θ在π/6～5π/6范圍內時，無限長V型薄板功率流透射損失差異不大，而當θ為π/36和π時，無限長V型薄板功率流透射損失差異明顯，說明V型薄板夾角接近0和π時，無限長V型薄板功率流透射損失對角度變化敏感，而在π/6～5π/6的較大角度范圍內，無限長V型薄板功率流透射損失對角度變化不敏感。圖5(b)表明，在非峰谷值區，無限長V型薄板功率流透射損失隨V型薄板夾角的增大而減小。由此說明，V型薄板夾角越大，越有利于板中功率流的透射。

2.3.2有限長V型薄板功率流透射損失

下面以兩對邊簡支另外兩對邊自由的有限長V型薄板為例，用MRRM研究V型薄板夾角、厚度和阻尼損耗因子等參數對其功率流透射損失的影響。

2．3．2．1V型薄板夾角對功率流透射損失的影響

圖6(a)表明，當θ≤π/6時，不同角度V型薄板功率流透射損失存在一定差異，且θ越小，該差異性越明顯。同時，隨著頻率的增加，同一夾角的V型薄板功率流透射損失的差異性也增大；圖6(b)表明，當π/6≤θ≤5π/6時，不同角度V型薄板功率流透射損失隨頻率的變化規律趨于一致，尤其是在較低頻段(180Hz以下)，其變化規律基本一致，而在較高頻段(180Hz以上)，其變化規律開始存在偏差，但偏差不大； 圖6(c)表明，當θ≥5π/6時，θ越大，不同角度V型薄板功率流透射損失差異性越明顯，而且隨著頻率的增加，該差異逐漸增大。

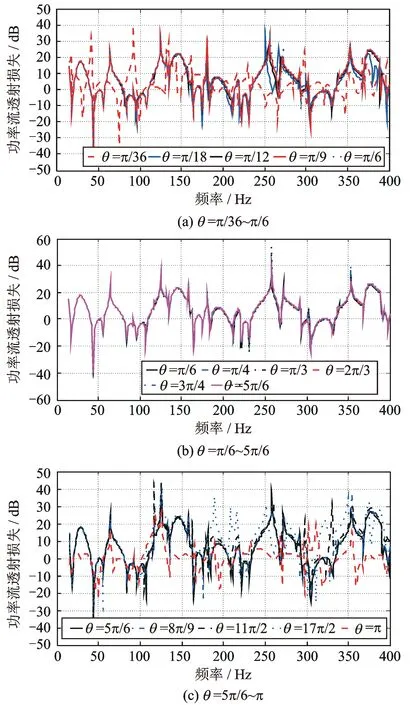
圖6　不同角度有限長V型薄板功率流透射損失Fig.6　TL of power flow through a finite V-shaped plate coupled with various angles

由此說明V型薄板連接處面內波與面外波的耦合效果與V型薄板夾角有關。在夾角較小和較大時，V型薄板連接處面內波與面外波的耦合效果十分顯著。

2.3.2.2V型薄板厚度對功率流透射損失的影響

圖7表明，不同厚度V型薄板功率流透射損失的變化規律差異較大。V型薄板板厚越薄，其在板接縫處的功率流透射損失越大，功率流透射損失峰值也越密集，而且，功率流透射損失峰值向高頻段偏移的特性也越明顯。

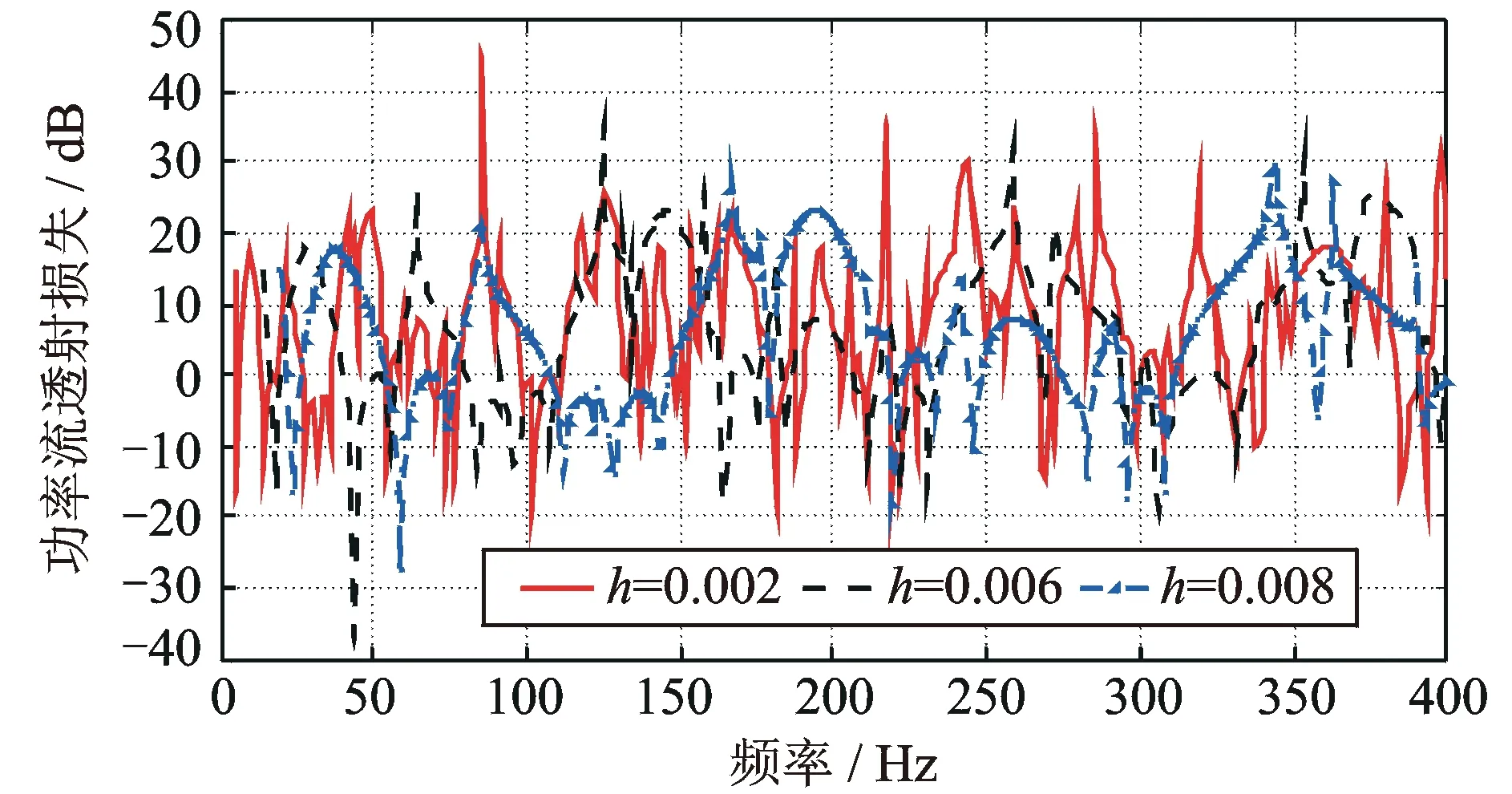
圖7　不同厚度有限長V型薄板功率流透射損失Fig.7　TL of power flow through finite V-shaped plates of different thickness

這表明V型薄板板厚越小，結構固有頻率越高，V型薄板中功率流透射損失也呈現峰谷密集出現這一高頻特征；同時，V型薄板板厚越小，V型薄板中面內波與面外波耦合效果越好，越有利于V型薄板中功率流透射。

2.3.2.3V型薄板阻尼對功率流透射損失的影響

圖8表明，阻尼對V型薄板功率流透射損失影響比較顯著。在較低頻段，阻尼越大，V型薄板在板接縫處的功率流透射損失也越大，但是，隨著頻率的增加，不同阻尼V型薄板在板接縫處的功率流透射損失逐漸趨于相同，且與無阻尼V型薄板在板接縫處的功率流透射損失基本相同， 即阻尼對低頻段V型薄板功率流透射損失影響較大，隨著頻率的增加，該影響逐漸減小。

圖8　不同阻尼有限長V型薄板功率流透射損失Fig.8　TL of power flow through finite V-shaped plates of different damping

這說明，在較低頻段，V型薄板中波長較大，功率流分布不均勻，因此，在板接縫處的功率流透射損失波動也越大；隨著頻率的升高，薄板中波長減小，功率流分布趨于均勻，在板接縫處的功率流透射損失波動也趨于相同。

3　結　論

本文基于Kirchhoff薄板理論，用波動法求解了兩對邊簡支邊界條件下的薄板運動微分方程，并用回傳射線矩陣法(MRRM)研究了V型薄板在簡諧點激勵力作用下的振動響應，并與有限元法(FEM)進行對比，得到了一致的結果。在此基礎上計算出V型薄板的功率流，進而得到了V型薄板板接縫處的功率流透射損失。然后，基于上述研究，本文分析了V型薄板夾角、板厚度和阻尼損耗因子等參數對V型薄板板接縫處的功率流透射損失的影響，得出如下結論：

(1)V型薄板連接處面內波與面外波的耦合效果與V型薄板夾角有關；在夾角較小和較大時，V型薄板連接處面內波與面外波的耦合效果十分顯著。

(2)V型薄板板厚越小，V型薄板中功率流透射損失呈現出峰谷密集的特征；同時，V型薄板板厚越小，V型薄板中面內波與面外波耦合效果越好，越有利于V型薄板中功率流透射。

(3)阻尼對低頻段V型薄板功率流透射損失影響較大，隨著頻率的增加，該影響逐漸減小。在較低頻段，阻尼越大，V型薄板在板接縫處的功率流透射損失也越大，但是，隨著頻率的增加，不同阻尼V型薄板在板接縫處的功率流透射損失逐漸趨于相同。

[1]Euler L. De motu vibratorio tympanorum. Novi commentari acad [J]. Petropolit, 1766, 10: 243—260.

[2]Kirchhoff G. Vorlesungen über Mathematische Physik[M]．Vol.1, B. G. Teubner, Leipzig, 1876.

[3]Love A E. A Treatise on the Mathematical Theory of Elasticity [M]. 4th ed. Cambridge: Cambridge University Press, 1926.

[4]Mindlin R D. Influence of rotatory inertia and shear on flexural motions of isotropic elastic plates [J]. J. Appl. Mech., 1951, 18: 31—38.

[5]Cuschieri J M. Structural power-flow analysis using a mobility approach of an L-shaped plate [J]. J. Acoust. Soc. Am., 1990, 87(3): 1159—1165.

[6]Cuschieri J M. Parametric analysis of the power flow on an L-shaped plate using a mobility power flow approach [J]. J. Acoust. Soc. Am., 1992, 91(5): 2686—2695.

[7]Cuschieri J M. In-plane and out-of-plane waves′ power transmission through an L-plate junction using the mobility power flow approach [J]. J. Acoust. Soc. Am., 1996, 100(2):857—870.

[8]Nicole J Kessissoglou. Power transmission in L-shaped plates including flexural and in-plane vibration [J]. J. Acoust. Soc. Am., 2004, 115(3): 1157—1169.

[9]CHEN Xiao-li, SHENG Mei-ping. Research on vibration characteristics of L-shaped plate using a mobility power flow approach [J]. Journal of Marine Science and Application, 2007, 6(3): 12—16.

[10]Liu Chun-Chuan. The wave and vibratory power transmission in a finite L-shaped Mindlin plate with two simply supported opposite edges [J]. Acta Mech. Sin., 2011, 27(5): 785—795.

[11]Lin Yongshui, Wu Weiguo, Li Xiaobin, et al. Study on transmission law of flexural waves through L-shaped steel-Aluminum joints [C]. Proceedings of the Twenty-second (2012) International Offshore and Polar Engineering Conference. Greece, Rhodes, 2012: 23—28.

[12]Lai Yuanming, Yu Wenbin. Analytical solution for forced vibration of a simply-supported V-shaped folded plate roof [J]. Thin-Walled Structures, 2002, 40: 215—223.

[13]Amin Paykani, Mehrdad Khosravi, Mohammad-Ali Saeimi-Sadigh. Dynamic analysis and design of V-shape plates under blast loading [J]. Journal of Vibroengineering, 2013, 15(2): 971—980.

[14]Thomson W T. Matrix solution for the vibration of non-uniform beams [J]. Journal of Applied Mechanics, 1950, 17: 337—339.

[15]Howard S M, Pao Y H. Analysis and experiments on stress waves in planar trusses [J]. Journal of Engineering Mechanics, 1998, 124:884—891.

[16]郭永強.回傳射線矩陣法的理論及其應用[D]. 杭州:浙江大學, 2007.

Guo Yongqiang. The method of reverberation ray matrix and its applications [D]. Hangzhou: Zhejiang University, 2007.

[17]鄭喜亮.基于回傳射線矩陣法的Timoshenko梁動力響應分析[D].杭州:浙江大學, 2007.

Zheng Xiliang. Dynamic response analysis of Timoshenko beams using the MRRM [D]. Hangzhou: Zhejiang University, 2007.

[18]諸駿,陳偉球,葉貴如,等.基于回傳射線矩陣法的迭代算法及其應用[J]. 中國科學G輯：物理學，力學，天文學, 2009, 39(1): 103—111.

Zhu Jun, Chen Weiqiu, Ye Guiru, et al. Iterative algorithm for the method of reverberation matrix and its application [J]. Sci. Sin-Phys., Mechs. Astron., 2009, 39(1): 103—111.

[19]劉春川.基于波動理論的有限尺寸結構短時瞬態響應與功率流控制[D].哈爾濱:哈爾濱工業大學,2011.

Liu Chun-Chuan. The short time transient responses and power flow control of structures with finite size based on the wave theory [D]. Harbin: Harbin Institute of Technology, 2011.

[20]Karl F Graff. Wave Motion in Elastic Solids[M]. New York: Dover Publications, INC., 1975: 230—234.

[21]Bercin A N, Langley R S. Application of the dynamic stiffness technique to the in-plane vibrations of plate structures [J]. Computers & Structures, 1996, 59(5): 869—875.

[22]Boisson C, Guyader J L, Millot P, et al. Energy transmission in finite coupled plates, Part Ⅱ: Application to an L-shaped structure [J]. J. Sound Vib., 1982, 81: 93—105.

[23]Cremer L, Heckl M,Ungar E E. Structure-borne sound [M]. 2nd ed.Berlin: Springer-Verlag, 1988:489.

[24]Park D H, Hong S Y, Kil F G, et al. Power flow models and analysis of in-plane waves in finite coupled thin plates [J]. J. Sound Vib., 2001, 244: 651—668.

[25]Pan X,Hansen C H. Active control of vibratory power transmission along a semi-infinite plate [J]. J. Sound Vib., 1995, 184: 585—610.

[26]Anthony J Romano, Phillip B Abraham, Earl G Williams. A pointing vector formulation for thin shells and plates, and its application to structural intensity analysis and source localization. Part I: Theory [J]. J. Acoust. Soc. Am.,1990, 87(3): 1166—1175.

Research on transmission loss of power flow through a finite V-shaped plate

TANGDong1,PANGFu-zhen1, 3,WANGQing-shan2,YAOXiong-liang1

(1.College of Shipbuilding Engineering, Harbin Engineering University, Harbin 150001, China;2.College of Mechanical and Electrical Engineering, Harbin Engineering University, Harbin 150001, China；3.92857Army of PLA, Beijing 100007, China)

Based on the Kirchhoff thin plate theory, the method of reverberation ray matrix (MRRM) is employed to study the transmission loss of power flow through a finite V-shaped plate. The V-shaped plate is supposed to be simply supported at two opposite edges and coupled with an arbitrary angle at the joint. Both of the effects of the flexural and in-plane waves are concerned. The V-shaped plate is discretized into different parts at the excitation point and the joint. A dual local coordinate system is established for each part of the discretized model. Accordingly, the scattering matrix of the V-shaped plate is obtained from the continuity and equilibrium conditions at the joint and the boundary conditions at each end. Subsequently, the phase matrix is derived from the inherent relations among the variable vectors expressed in the dual local coordinate system. Then the reverberation matrix of the V-shaped plate is derived. Therefore, a model for dynamic response analysis of the V-shaped plate is established. Then the dynamic response of a V-shaped plate subjected to a harmonic point force is analyzed by MRRM, and the calculation results are compared with those obtained by FEM. It is found that MRRM is of high accuracy and efficiency. Finally, power flow of the V-shaped plate is calculated, and the effects of coupling angle, plate thickness and damping loss factor on transmission loss of power flow through the V-shaped plate are also investigated.

structural dynamic analysis; power flow; transmission loss; V-shaped plate; method of reverberation ray matrix

2014-06-06；

2015-07-03

國家自然科學基金資助項目(51209052)；黑龍江省青年科學基金資助項目(QC2011C013)；哈爾濱市科技創新人才研究專項資金資助項目(2011RFQXG021)；上海交通大學海洋工程國家重點實驗室基金資助項目(1307)；中央高校基本科研業務費資助項目(HEUCF40117);國防預研項目(4010403010103)

O342; TB532

A

1004-4523(2016)01-0112-11

10.16385/j.cnki.issn.1004-4523.2016.01.015

湯冬(1991—),男, 博士研究生。電話：15764508298；E-mail：tangdong@hrbeu.edu.cn