解析幾何核心完美突破
張紅紅
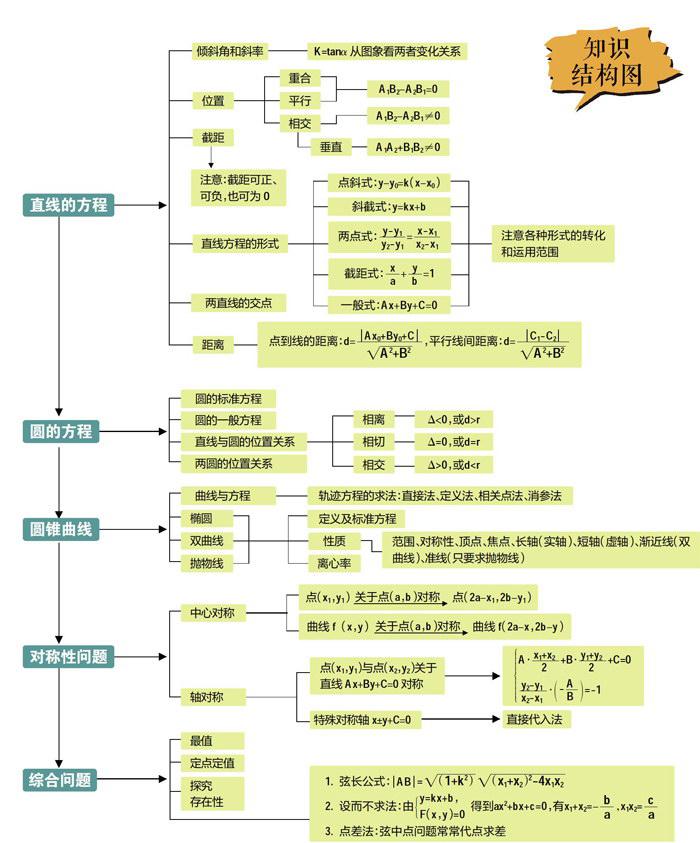


解析幾何板塊在高考中占有十分重要的地位,出題形式為:必做題中往往有一道或兩道客觀題(5或10分)和一道主觀題(12至14分),選做題中的坐標系與參數方程(10分)后者的知識結構和方法應用實質上也屬于解析幾何,只是坐標系的選取和方程的表現形式發生了變化。
重要考點分布規律為:(1)圓、橢圓、雙曲線和拋物線的定義、標準方程與圖形的幾何性質常常出現在客觀題和主觀題的第一小題,屬于低、中檔題;(2)與直線和圓錐曲線的位置關系相關的問題(如弦長、三角形面積、夾角等數量關系等)常常出現在主觀題中的第二小題,屬于難題由于考查重點和難點聚焦在最值、定點定值、探究存在性這些熱點問題上,所以同學們的復習備考也是有章可循的。
考點1:直線和圓
名師圈點
在求過某點A(m,n)的圓的切線方程時,應先判斷點與圓的位置關系,若點在圓上,切線有且只有一條;若點在圓外,切線必有兩條,此時如果僅求得一條。則漏了斜率不存在的情況,即x=m,應補上。
考點2:圓錐曲線的定義、標準方程與圖形的幾何性質
命題點
(1)圓、橢圓、雙曲線和拋物線的定義、標準方程與圖形的幾何性質;
(2)離心率的計算方法;
(3)焦半徑的范圍;
(4)軌跡方程的求法.
名師圈點
焦點三角形PFlF2中,常常想到圓錐曲線的定義,從而通過己一知建立a,b,c的關系以便解出離心率。
名師圈點
如果所給幾何條件能夠確定動點軌跡符合橢圓、雙曲線、拋物線。圓等曲線的定義,則?可直接利用,曲線定義寫出方程.這種方法稱為定義法(條件中常含有兩對稱的定點。一定點和一定直線、線段的中垂線、兩圓相切等幾何條件)。
考點3:圓錐曲線中的最值問題
(1)求數量積的最值;
(2)求線段長度的最值; (3)求三角形面積的最值.常常要注意字母隱含的范圍(如直線與圓錐曲線相交時,△>0;圖形上的點的坐標的約束范圍等)
考點4:圓錐曲線中的存在性問題
(1)探究符合某條件的點的存在性;
(2)探究符合某條件的直線的存在性;
(3)探究符合某條件的圖形的存在性.
名師圈點
解決存在性問題的方法為:先假設存在,由已知或假設等推出矛盾則不存在;找到了存在的對象且沒有推出矛盾.則由推理論證可知存在。
考點5:圓錐曲線中的定點定值問題
(1)探究某圖形過定點;
(2)探究某代數式為定值.
名師圈點
證明或探究定值問題,常常設出相關點的坐標或相關直線的方程,結合幾何圖形通過代數運算化簡消參得定值。

