基于演化博弈的新型農產品批發模式構建問題探討

■ 姚冠新　教授　何　勇　通訊作者　邊曉雨（、江蘇大學管理學院　江蘇鎮江　2203　2、揚州大學　江蘇揚州　225009）

基于演化博弈的新型農產品批發模式構建問題探討

■ 姚冠新1、2教授何勇1通訊作者邊曉雨1（1、江蘇大學管理學院江蘇鎮江2120132、揚州大學江蘇揚州225009）

本文針對新型農產品物流園區模式構建過程中多方主體參與的問題，建立了農戶、批發商、地方政府的三方演化博弈模型。引入政府補貼、收益、合作投資、產業升級成本、風險成本、超額收益等變量，對博弈模型進行求解，并對演化結果相關變量進行靈敏度分析，從而得出對新模式構建過程中各主體行為以及農產品物流從傳統批發模式向一體化、產業化運作模式推進過程的相關對策與建議。

農產品物流模式物流園區三方演化博弈

引言

當前我國以批發商為主導的農產品物流模式仍然存在著諸多缺陷和不足。近年，我國也出現了以批發市場為核心的物流園區模式，并受到相關學者關注，如張京敏（2015）通過對比中外農產品物流發展模式，提出切合中國實際情況的本土農產品物流發展新思路：即形成以農產品物流園區為核心，聯合農村合作社，通過一定的協議，相互合作、共擔風險的中國農產品物流的未來發展模式。

當前，對于新型農產品批發物流園區模式有了一些研究，但對此模式下相關主體關系的研究依然很少。因此，本文針對近年來我國新興起的農產品物流園區模式以及其構建過程出現的多方主體參與的現象，構建三方演化博弈模型，研究傳統的批發商主導模式向新的批發商主導的物流園區模式演進過程。關于三方演化博弈問題，也有部分學者在生態鏈企業穩定性等方面進行過相關研究，本文參考上述學者的三方博弈模型，研究了新興農產品物流模式的構建演化過程，以期為農產品產業化、集成化、一體化物流模式發展提供一些建議。

模型構建與分析

（一）模型基本假設

假設1：參與人假設模型中有三個參與人，分別為當地政府、批發商、農戶合作組織，三方均滿足“理性經濟人”假設，在客觀條件的約束下都會追求自身利益的最大化。在一個“自然”環境中，各主體均具有限理性且具有較強學習模仿能力，可以通過對比其他主體策略及收益情況調整策略。

假設2：參與人效益假設通過多主體參與的農產品物流模式構建，地方政府可增加財政收入和實現社會效益；批發商可以通過新型農產品產業鏈模式獲得更大的經濟效益，并可獲得政府更多的支持和稅收等政策上的優惠；農戶合作組織可以提高農產品生產技術獲得更多、更穩定的經濟收入。

假設3：行動方案假設政府的行動方案有兩種，即對新型農產品物流產業園區模式構建給予政策上的支持和不支持兩種態度；對于批發商來說，可以積極構建農產品物流園區和消極構建兩種態度；對于農戶合作組織來說，可以選擇與批發商積極合作進行技術升級也可以選擇不合作。

當地政府選擇支持構建的概率為x，則選擇不支持的概率為1-x；批發商選擇積極構建的概率為y，則選擇消極構建的概率為1-y；農戶合作組織選擇合作的概率為z，則選擇不合作的概率為1-z。

表1　新模式構建時三方主體收益矩陣

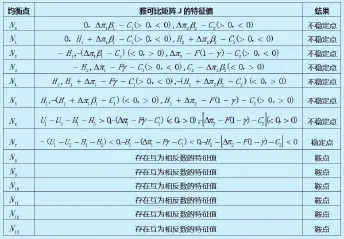
表2　雅克比矩陣均衡點的局部穩定性

（二）模型構建

當地政府的相關損益：當采取支持構建策略時，當地政府需要在政策上對批發商、農戶給予支持，比如稅收優惠或者補貼等其它支持，這里統一界定為一項成本費用H1、H2，當政府采取不支持的策略時就無需向批發商支付任何費用，此時獲得額外收益為U2。新模式構建起來會帶給政府額外收益U1。

批發商的相關損益：若當地政府支持構建便可得到資金支持，政府不支持則為0；批發商若選擇積極構建物流園區需支出成本為C1，消極構建不需要支付額外成本，沒有政府補貼支持；在農戶選擇不合作的情況下消極構建可獲得的收益為π1，在農戶合作情形下選擇積極構建可獲得超額收益為Δπ1，同時雙方會面臨F的風險成本，批發商承擔風險系數為γ，農戶不合作時積極構建時超額收益系數為β1，農戶合作時選擇消極構建超額收益為0。

農戶合作組織相關損益：若當地政府支持構建可從政府得到H2的資金支持，政府不支持則為0；農戶若選擇合作需支出技術升級成本C2，不合作不需要支付額外成本，沒有政府補貼支持；在批發商選擇消極構建的情形下選擇不合作可獲得收益為π2，在批發商選擇積極構建的情形下選擇合作可以獲得超額收益Δπ2，同時雙方面臨共擔的風險成本F，農戶承擔的風險系數為（1-γ），批發商消極構建時選擇合作時超額收益系數為β2，批發商積極構建時選擇不合作超額收益為0。

三方主體收益矩陣如表1所示。

U11表示當地政府采取策略支持時的期望收益，則：

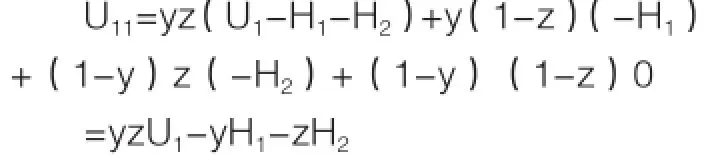
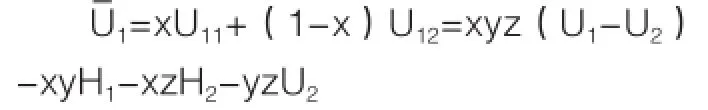
可得，當地政府采取支持策略比例的動態復制方程為：

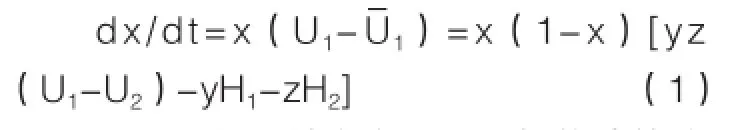
同理可得，批發商采取積極構建策略比例的動態復制方程：

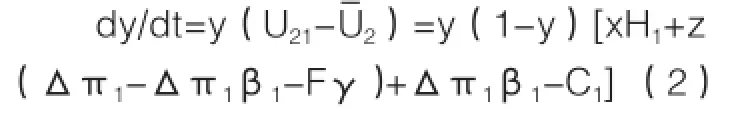
同理，農戶采取合作策略比例的動態復制方程為：

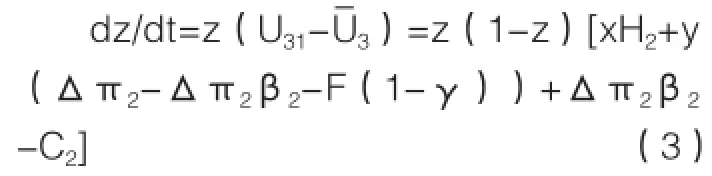
令dx/dt=0，dy/dt=0，dz/dt=0得出14個均衡點分別為N0（0，0，0），N1（1，0，0），N2（0，1，0），N3（0，0，1），N4（1，0，1），N5（1，1，0），N6（0，1，1），N7（1，1，1），

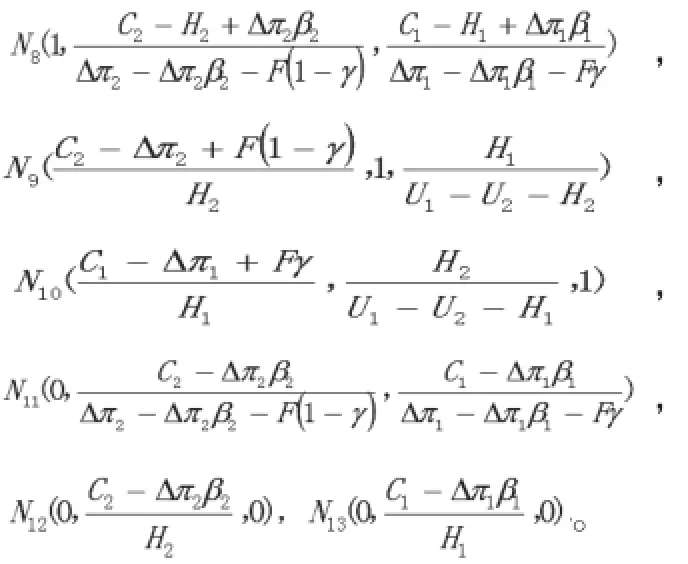
由微分方程（1）、（2）、（3）得出雅克比矩陣為J：

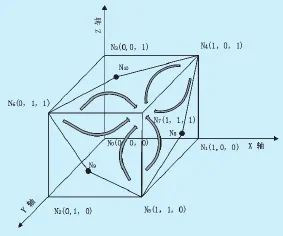
圖1　均衡點局部穩定性及進化路徑分析

演化路徑分析

根據模型的假設，當地政府采取支持、批發商采取積極構建、農戶采取合作策略時，博弈三方的合作能夠達成，新模式得以構建并運行，此時三方獲得的收益（直接收益+間接收益）大于其采取對應策略的成本U1＞H1+H2，Δπ1+H1＞C1+Fγ，Δπ2+H2＞C2+F（1-γ）。任一初始點及其演化后的點在三維空間內才具有意義。

1.若U1-U2＜H1+H2，Δπ2＜Δπ2β2+ F（1-γ），Δπ1＜Δπ1β1+ Fγ：

即意味著當農戶和批發商積極合作時，當地政府采取支持的最終受益比采取不支持的最終受益少，顯然此時“不支持”是當地政府的占優策略；當批發商堅決采取積極構建時與農戶達成合作一致構建起新模式產生的最終受益小于因農戶不合作而未構建起新模式的最終收益；同樣當農戶堅決采取合作時批發商采取積極時農戶最終收益小于因批發商消極構建而未構建起新模式的最終收益。現實意義是當地政府、批發商和農戶積極合作的積極性受到風險成本過高因素的打擊而喪失積極性。導致博弈方長期博弈結果偏離｛支持，積極，合作｝。如此是不利于博弈各方之間合作構建新模式，因此不做詳細討論。

2.若U1-U2＞H1+H2，Δπ2＞Δπ2β2+ F（1-γ），Δπ1＞Δπ1β1+ Fγ：

演化博弈中存在采取不合作（不支持、消極）策略的博弈方，而其他主體選擇合作（積極、支持）情形下獲得的超額收益足以補償其直接成本，即Δπ1＞C1+ Fγ，Δπ2＞C2+ F（1-γ），Δπ1β1＞C1，Δπ2β2＞C2，點N8、N9、 N10、N11、N12、N13不在演化博弈的三維空間內dx/dt=0，x=0，x=1是x的穩定狀態，其中x=1是進化穩定策略，同理是y=1，z=1是進化穩定策略，均衡點為進化穩定點，即｛支持，積極構建，合作｝為進化穩定策略。因此只要超額收益足以彌補風險及成本，長期博弈結果為｛支持，積極構建，合作｝。

演化博弈中存在采取不合作（不支持、消極）策略的博弈方，而其他主體選擇合作（積極、支持）情形下獲得的超額收益不足以補償其直接成本Δπ1β1+H1＜C1，Δπ2β2+H2＜C2，Δπ1＜C1+ Fγ，Δπ2＜C2+F（1-γ），Δπ1β1＜C1，Δπ2β2＜C2時點N11、N12、N13不在演化博弈的三維空間內。點N8在面S1=｛x，y，z（x=1，0＜y＜1，0＜z＜1）｝上，點N9在面S2=｛ x，y，z （0＜x＜1，y=1，0＜z＜1）｝上，點N10在面S3=｛ x，y，z（0＜x＜1，0＜y＜1，z=1）｝上，借助雅克比矩陣J對均衡點的局部穩定性進行分析（見表2）。

由表2可知均衡點（1，1，1）為進化穩定點，均衡點為鞍點。進化路徑如圖1所示。

當Δπ1＞C1+ Fγ，Δπ2＞C2+F（1-γ），Δπ1β1＞C1，Δπ2β2＞C2時，由圖1可知如果博弈三方的初始狀態落在區域Ⅰ、Ⅱ、Ⅲ內，博弈行為將演化到點，即演化到｛支持，積極，合作｝的策略；演化到點的可能性與區域Ⅰ、Ⅱ、Ⅲ的面積有關，面積越大演化到點的可能性越大。影響區域Ⅰ、Ⅱ、Ⅲ面積的參數的方向與博弈進化的方向一致，由圖1可知區域Ⅰ、Ⅱ、Ⅲ的面積S為：

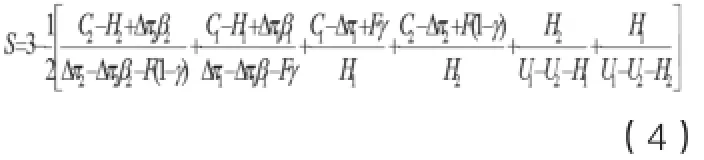
演化博弈結果分析

演化博弈中存在采取不合作（不支持、消極）策略的博弈方，而其他主體選擇合作（積極、支持）情形下獲得的超額收益足以補償其直接成本，即Δπ1＞C1+ Fγ，Δπ2＞C2+F（1-γ），Δπ1β1＞C1，Δπ2β2＞C2時｛支持，積極，合作｝為進化穩定策略。因此只要超額收益足以補償其直接成本時博弈各方主體間的長期博弈結果為｛支持，積極，合作｝。

演化博弈中存在采取不合作（不支持、消極）策略的博弈方，而其他主體選擇合作（積極、支持）情形下獲得的超額收益不足以補償其直接成本即Δπ1β1+H1＜C1，Δπ2β2+H2＜C2，Δπ1＜C1+ Fγ，Δπ2＜C2+F（1-γ），Δπ1β1＜C1，Δπ2β2＜C2時，由式（4）可知影響各博弈主體間合作構建新模式的參數包括合作超額收益Δπi、Δπiβi、Ui，成本Ci、Hi、F（i=1，2），收益系數風險系數γ、β。根據式（4）分析各參數對新模式構建的影響：

新模式構建后的超額收益：

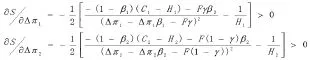
因此S為Δπi的增函數，隨著新的農產品批發模式的構建所得超額收益Δπi的增加，S逐漸增大，博弈演化到點N7（1，1，1）的可能性增大。

新模式給政府帶來的效益Ui：

因此S為U1的增函數，隨著新的農產品批發模式的構建政府采取支持策略所得效益U1的增加，S逐漸增大，博弈演化到點N7（1，1，1）的可能性增大。

因此S為U2的減函數，隨著新的農產品批發模式的構建政府采取不支持策略所得效益U2的增加，S逐漸減小，博弈演化到點N7（1，1，1）的可能性減小。

構建新模式的成本Ci：

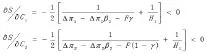
因此S為Ci的減函數，隨著新的農產品批發模式的構建所需成本Ci的增加，S逐漸減小，博弈演化到點N7（1，1，1）的可能性減小。

當地政府補貼Hi：

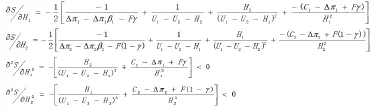
當H1→0時，H1→U1-U2時，＜0，在（0，U1-U2）遞減，因此存在H1，使

同理可得，在（0，U1-U2）內存在H2，使

那么，在（0，U1-U2）上一定范圍內隨著當地政府補貼的增大，S增大，后來隨著其增大而減小，H1+H2＜U1-U2。

新模式下批發商與農戶的風險成本F：

因此S為F的減函數，隨著新的農產品批發模式的構建批發商與農戶間合作風險成本F的增加，S逐漸減小，博弈演化到點N7（1，1，1）的可能性減小。

新模式未構建，但批發商、農戶一方積極合作時的超額收益系數βi：

因此S為βi的減函數，隨著新模式未構建時批發商、農戶一方積極合作的超額收益系數βi增大，S逐漸減小，博弈演化到點N7（1，1，1）的可能性減小。

新模式構建時批發商與農戶間的風險分配系數γ：

分配系數γ對S的影響與其它多個系數相關，單調性在此難以細化深入具體分析，因此省略。

由上述分析可知，通過提高新模式構建后帶給批發商、農戶的超額收益以及當地政府的效益，降低當地政府不支持時的效益以及批發商和農戶的構建成本，確定最佳的政府補貼，減小新模式下批發商與農戶間的合作風險及僅一方積極合作時積極一方的超額收益系數，確定最佳的風險分配系數能夠促進新農產品批發模式構建的各個主體積極合作支持，從而保障建立統一的農產品批發模式。

從上述研究可以看出，在現有批發商主導的農產品物流模式下要想建立起新型批發商主導的農產品物流園區模式，需要當地政府、批發商、農戶多方共同配合積極合作，涉及構建成本、政府補貼、新模式運行效益等多方面問題，對此從以上分析出發，筆者提出相關建議。

當地政府在新模式的構建過程中起著促進和推動的作用，因新模式下物流園區的構建需要大量的成本，政府給予批發商及農戶一定補貼，新模式構建起來之后，能給當地政府帶來經濟或其它效益，在一定范圍內增加補貼力度有利于促進批發商、農戶積極合作建設，但是過高的補貼容易導致出現“搭順風車”的現象以及政府得不償失的局面。因此，適度的補貼才是理性促進批發商和農戶積極合作構建新模式的舉措。

批發商在新模式下依然處于主導地位，是新模式的最大受益者，而新模式的物流園區建設也需要批發商付出相當的成本，同時在與農戶間的合作關系中也承擔著合作風險，因此設法使新模式下批發商的收益顯著提高，可通過政府補貼，充分利用新的模式下的技術優勢探討合理的交易合作機制，更準確地預測市場需求以充分降低風險以及交易等成本，才能促使批發商以更強的動力構建新模式，并發揮出新模式的優勢。

農戶是農產品的輸出者，是生產主體，一直以來農戶在我國農產品交易過程當中多處于弱勢地位。在新模式中，通過政府協調批發商與農戶合作組織間進行更為緊密的對接合作，農戶地位得到提升，但是農戶需要進行產業技術升級，以向批發商提供更加優質、產量穩定的農產品，因此為減少農戶參與合作的阻力，政府需為農戶提供技術支持以及產業技術升級的補貼，促進監督與批發商間良好的合作以降低風險，保障農戶在合作過程中的切實利益。

1.劉聯輝，文珊.我國農產品物流系統模式革新趨勢及其構筑策略［J］.農村經濟，2006（5）

2.賀峰.中國農產品物流模式構建：基于批發市場的研究［J］.農業技術經濟，2006（5）

3.寇平君，盧鳳君.構建我國農產品市場流通模式的戰略性思考［J］.農業經濟問題，2002（8）

4.盛革.我國農產品現代流通服務體系的協同優化設計［J］.管理評論，2009（8）

5.趙曉飛.我國現代農產品供應鏈體系構建研究［J］.農業經濟問題，2012（1）

6.李建平，王吉鵬，周振亞等.農產品產銷對接模式和機制創新研究［J］.農業經濟問題，2013（11）

7.張京敏，王如暉.中國農產品物流模式探討—基于中外農產品物流模式的對比分析［J］.熱帶農業工程，2015，39（1）

8.楊軍，葛孚橋.現代農產品物流體系建設與運行的財政支持政策探討［J］.生態經濟，2011（3）

9.周甜甜，王文平.基于演化博弈論的生態產業鏈穩定性研究［J］.科技與經濟，2014，27（1）

10.吳瑞明，胡代平，沈惠璋.流域污染治理中的演化博弈穩定性分析［J］.系統管理學報，2013，22（6）

11.翟麗麗，柳玉鳳，王京等.軟件產業虛擬集群企業間信任進化博弈研究［J］.中國管理科學，2014（12）

12.魏芳芳，陳福集.網絡虛假信息中政府、企業和公民三者的進化博弈行為分析［J］.運籌與管理，2012，21（6）

國家自然科學基金（71540013，71473213）；江蘇省高校哲學社會科學重點項目（2014ZDIXM019）

F274

A