多進制GMSK頻譜分析及解調算法
李春騰,張曙霞,李崇遠
(海軍工程大學 電子工程學院,湖北 武漢 430033)
?
多進制GMSK頻譜分析及解調算法
李春騰,張曙霞,李崇遠
(海軍工程大學 電子工程學院,湖北 武漢 430033)
多進制GMSK具有較大的頻譜效率優勢,對提高通信的效能有十分重要的意義。首先在二進制GMSK信號頻譜的基礎上,對多進制GMSK信號的頻譜進行簡要介紹,并對其進行比較,其次借鑒二進制GMSK信號的產生和解調思路,研究了多進制GMSK的產生算法及解調方式,并提出了對多進制GMSK信號的準最佳最大似然比解調算法,并對該算法進行仿真,結果發現該算法能夠取得較好的誤碼性能。
多進制;GMSK;頻譜;解調算法
0 引言
由于GMSK的窄帶寬和恒包絡特性,它獲取的頻譜效率與MSK[1]相比要高很多,因此人們針對GMSK的調制解調展開了深入的研究,采用非相干解調與相干解調[2]在GMSK的信號中均有應用[3-4]。美國的Bruce提出了多進制GMSK調制的算法[5],在衰減信道條件下將網格編碼調制和多進制GMSK調制結合在一起,對補償網絡進行了引進,這樣系統性能就不會受碼間串擾更多的影響,誤碼率顯著降低,但Bruce并未給出解調方法,這也是本文研究的重點。
在數字通信技術不斷發展的過程中,隨著不斷提高的通信需求,傳輸的信號會受到信道帶限與信道非線性的影響。在研究和分析這些技術的過程中,人們重點關注節省頻譜的方式以及如何高效應用頻譜。對基帶碼元信號進行多進制的調制,屬于一種非常有效的辦法,多進制GMSK作為恒包絡技術的一種可應用于非線性的信道條件下,能夠保證頻帶范圍比較小[6-7]。
1 多進制GMSK信號的調制
假設數字基帶信號表示為:
(1)
式中,T代表的是碼元維持時間的長短,In則為包含信息的序列,用二進制表示,g(t)表示的是高斯最小頻移鍵控(GMSK)脈沖,其中包含帶寬參數值B,用公式表達如下:
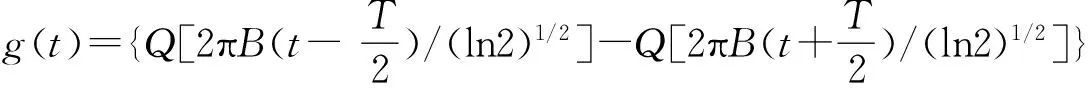
(2)
(3)
在實際應用中,式(2)可以當作是由經過高斯低通濾波器的矩形脈沖rect(t)所生成的,如式(4):
g(t)=h(t)*rect(t);
(4)
h(t)為濾波器的沖激響應為:
(5)
可以通過傅里葉變換來獲取濾波器的頻率特征:
H(f)=exp[-(ln2/2)(f/B)2]。
(6)
2 多進制GMSK頻譜比較與分析
首先對二進制GMSK信號的頻譜進行分析。首先是讀入分析參數,包括符號的總長度N,對信號的采樣頻率fs,碼元的傳輸速率Rb和一個碼元周期的采樣點數,即過采樣比OSR;然后產生伯努利分布的01二進制序列,序列需進行極性轉換,變為雙極性的非歸零二進制序列NRZ;接著對該序列進行差分編碼的預編碼;對預編碼后的比特序列要進行串并轉換,展寬后變成I路和Q路兩路比特流;接下來的工作是高斯濾波器的設計,首先是高斯濾波器的3 dB帶寬參數BT值設定為0.3,然后根據高斯脈沖的階數確定高斯成形脈沖的延時,最后由濾波器函數確定出濾波器系數;接著是將I路和Q路信號組成復信號I+jQ,同設計好的高斯濾波器系數卷積,并去除濾波器帶來的延時,得到高斯脈沖積分后的值;取積分后的實部和虛部對應和正弦型加權函數相乘,分別得到基帶信號的I路和分量,最終合成復基帶GMSK信號;然后是對合成的復基帶信號進行分段,對每段分別作傅里葉變換,對每段的結果取平均;最后根據采用頻率fs和每段的數據長度,控制畫出其基帶信號的頻譜[11]。
對頻譜分析主要從數據分段數和每段數據長度進行著手。具體來說,分段數和每段數據長度成制約關系,由圖1可以看出,當分段數越少時,每段數據長度越長,頻譜的能量泄漏越少,頻率分辨率也就提高了,但各個頻率成分的“毛刺”會有所增加,這是因為分段數較小時樣本數少,分段取平均不能很好地反映各個頻率分量實際大小,所以在頻譜分析中要對數據分段數和每段數據長度的取值作一定折中,以便更好地進行頻譜分析。
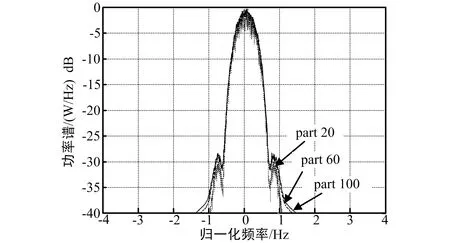
圖1 不同分段數對頻譜分析的影響
多進制GMSK信號頻譜的分析區別于二進制主要體現在信號產生這一方面。對于四進制,可將符號比特作電平映射,得到四進制的電平值,即sym的NRZ序列;另外調制指數通過改變I路和Q路的正弦型加權函數的相關參數,指導多進制復基帶GMSK信號的產生。
研究和分析不同調制階數M對信號頻譜的影響程度,分別從二進制GMSK(BGMSK)、四進制GMSK(4GMSK)和八進制GMSK(8GMSK)的功率譜密度著手分析,對于頻率均作歸一化處理,且對于高階的調制也均折算為1 bit的功率譜密度。首先整體上由于是復數基帶,幾個功率譜的正負頻率略有不對稱。對比特歸一化后,對比不同階數的功率譜密度,可以發現階數越高,功率譜帶外衰減更快,主瓣寬度更窄,以主瓣衰減10 dB為參考線,可得出不同階數GMSK信號的主瓣寬度之比l2GMSK:l4GMSK:l8GMSK約為1:0.708 0:0.598 5,這說明多進制GMSK調制的1 bit帶寬更窄,頻率效率越高。這和調制指數h存在一定關系,當調制階數越高,h越小,相位越連續,帶外功率譜越低,帶外功率譜下降越快,但隨著階數提高獲得的1 bit帶寬相對增益會減少。
3 多進制GMSK信號的解調
由于多進制GMSK信號調制[12-13]涉及的較高階數帶來的計算和系統設計的復雜程度,所以對其解調算法的探究除需借鑒二進制GMSK的相關解調方式,還要充分考慮多進制調制系統的自身特點,找到最優的解調方式。本節提出一種基于準最佳最大似然算法的軟判決檢測,這種軟判決算法是所研究和推廣的多進制GMSK解調算法的重點。
以最佳接收機的二進制GMSK解調理論為基礎,向多進制解調理論進行推廣,對在幾個信號傳輸間隔中,利用互相關的辦法,通過GMSK信號記憶的特征,可有如下解調思路的分析。可把接收信號進行如下表示:
r(t)=s(t,d1,Dk)+n(t)。
(7)
這里,可以把首個待檢測碼元計為d1,把觀察序列的n-1個碼元計為Dk={d2,…,dn}。從相干檢測的角度來說,可以把初始相位φ設置為零,通過最佳接收機能夠得到最大似然比:
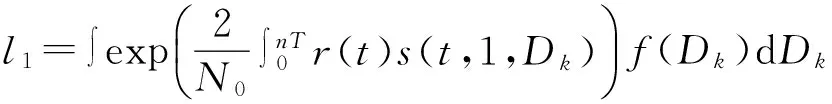
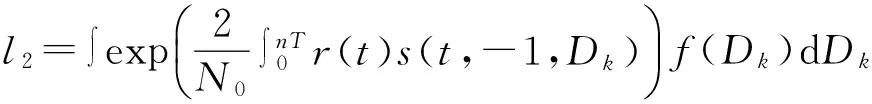
?
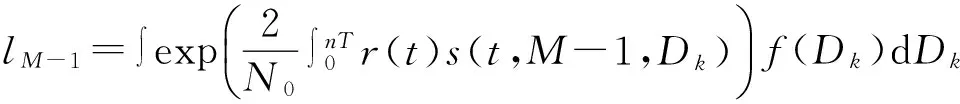
(8)
f(Dk)用來表示被觀察序列Dk的離散的概率密度函數(PDF),∫f(Dk)dDk則用來表示n-1重積分∫∫…∫f(d2)f(d3)…f(dn)dd2dd3…ddn,其中每個離散PDFf(dμ)是一系列沖激函數δ的組合:
(9)
Dk序列所有可能數量為Mn-1=m種,所以對D的積分可等價于:
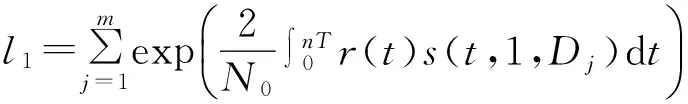
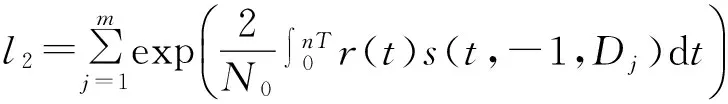
?
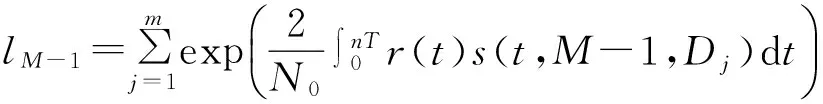
(10)
由上面的l值,可以做出相關的判決,最終得到d1。采取準最佳解調的思路:假如所觀測序列可以設定出一個長度為n,在進行檢測時,每一次檢測都對各個組的碼元長度為n的所接收的波形進行相關性計算。在去除指數運算和累加運算基礎上,取出Mn路的相關輸出最大的那一路的序列,則當前這一組碼元的值判為當前這一路輸入的參考信號s對應的碼元序列。
通過以上分析,可得4GMSK誤碼率的程序分析框圖,如圖2所示。其中BT為高斯濾波器的3 dB帶寬參數,Tb為碼元時間,N為碼元序列長度,OSR為過采樣比,T為每次觀測序列的長度,K=4T表遍歷個數,SNRpBit為歸一化1比特信噪比參數。首先根據給定觀測序列長度遍歷所有K個序列的波形,接著在不同信噪比條件下,生成N×T序列長度對應的波形,加噪聲,然后利用準最佳最大似然比算法,進行波形檢測,最后輸出其誤碼率。
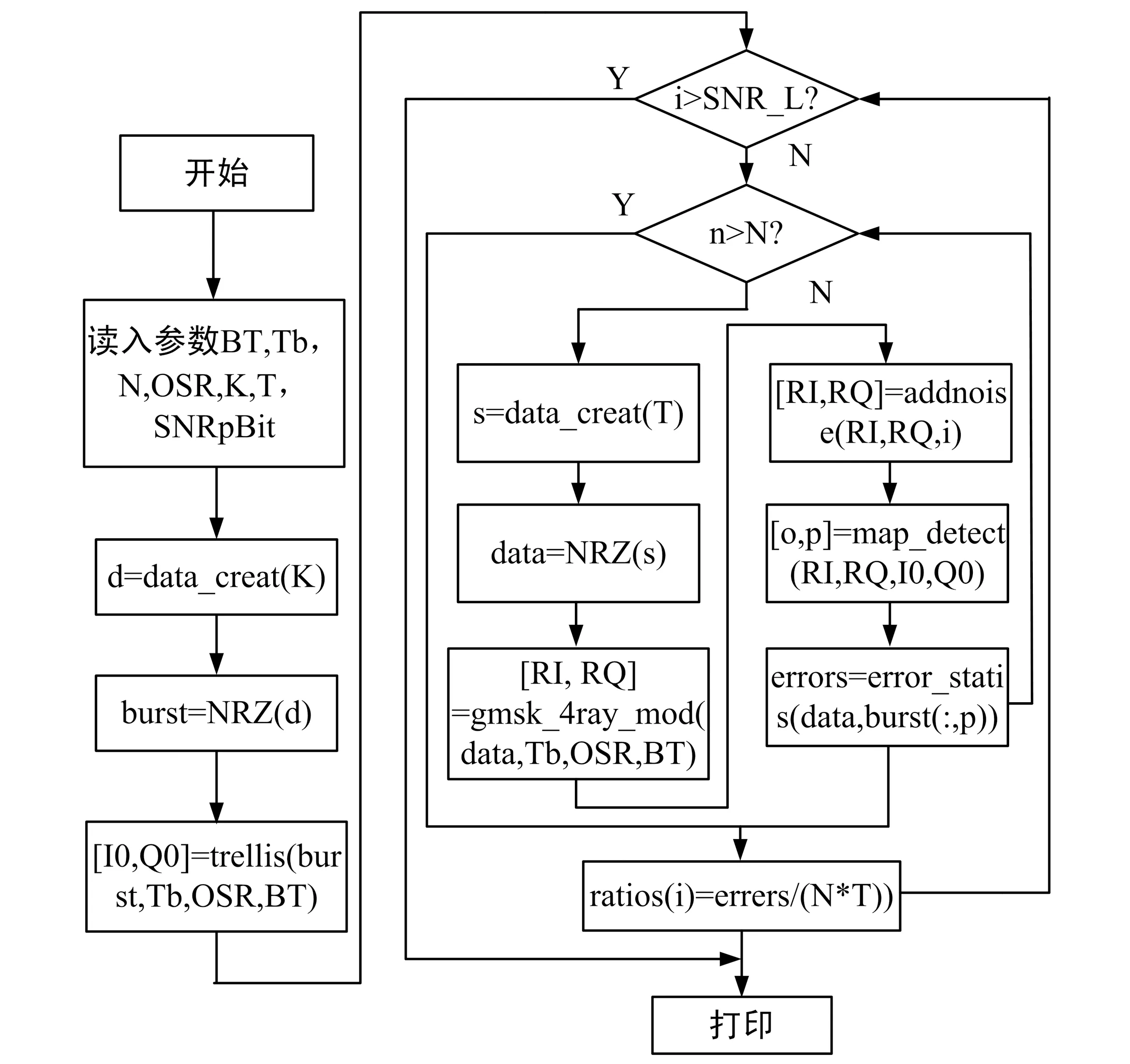
圖2 4進制GMSK誤碼率分析流程
對于多進制調制,其最佳誤碼率性能表達式為[5]:
(11)
把不同進制的誤碼率均折算為1 bit碼元的誤碼率進行比較。并通過MATLAB對其進行仿真[14],結果如圖3所示。通過圖3可知,調制階數M在不斷地增加,傳輸1 bit碼元所需的信噪比也隨之增加。這和調制指數h存在一定關系,當M增大時,h越小,相位越連續,而且載波的終值相位狀態增加,從相位星座圖上來看,當信噪比小于一定門限值時,噪聲容限減小,模糊了相位終值狀態點之間的差別,接收機很難準確判定調制時的相位終值狀態及其轉移路徑,故性能有所下降。通過上節分析可知,為使頻帶的利用率得到進一步提升,且1 bit帶寬隨著階數提高而減小,可以利用多進制GMSK進行調制來獲取誤碼率和頻譜效率的折中效益。
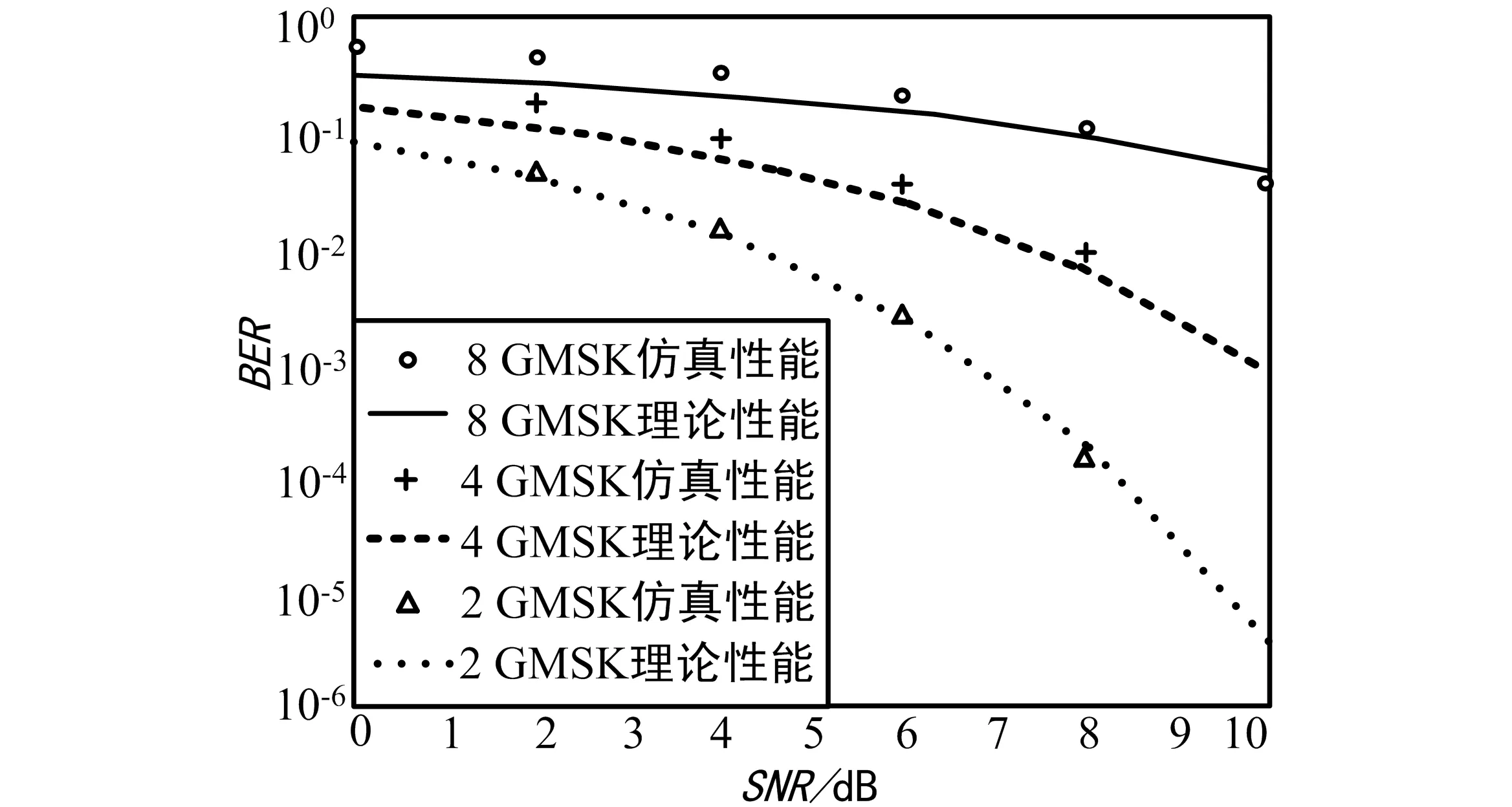
圖3 不同進制的GMSK誤碼性能
4 結束語
本文提出了多進制GMSK信號的產生及解調算法,比較和分析了不同階數的GMSK頻譜,結果顯示不同階數GMSK信號的主瓣寬度之比l2GMSK:l4GMSK:l8GMSK約為1:0.708 0:0.598 5,這說明多進制GMSK調制的1 bit帶寬更窄,頻率效率更高。還對多進制GMSK信號如何解調進行了研究和分析,主要是基于最佳接收機的準最佳最大似然算法的檢測。
GMSK因其良好的頻譜特性受到廣泛關注,除了進行多進制方面的研究,還可考慮結合其他恒包絡調制方式[15],如SOQPSK、TFM等,實現聯合調制,可使系統性能進一步優化。
[1]Bims H V,Cioffi J M.Trellis Coding with M-ary MSK Constraints[J].IEEE Global Telecommunications,1989,18(21):1546-1550.
[2]Gee L L.Threshold Detection Performance Of GMSK Signal With BT=0.5[J].IEEE Transactions on Communication,1998,2(23):515-519.
[3]熊于菽.GMSK調制解調技術研究[D].重慶:重慶大學,2007:24-32.
[4]丁興文.基于維特比算法的GMSK信號非相干解調技術研究[J].遙測遙控,2011,32(1):18-21.
[5]Cochran B.Development and Application of M-ary Gaussian Minimum Phase Shift Keying modulation[J].IEEE International Conference on Communications,1995,21(3):1805-1810.
[6]Bims H V,Cioffi J M.Trellis Coding with M-ary MSK constraints[J].IEEE Global Telecommunications,1989,18(21):1546-1550.
[7]樊昌信,曹麗娜.通信原理(第6版)[M].北京:國防工業出版社,2010:241-251.
[8]Murota K,Hirade K.GMSK Modulation for Digital Mobile Radio Telephony[J].IEEE Transactions on Communications,1981,29(7):1044-1050.
[9]丁陽,韋志棉.高斯最小頻移鍵控的實現方法研究和仿真[J].無線電工程,2006,36(3):32-34.
[10]U S Patent and Trademark Office.SICOM,INC.Data Communication Modulation with Managed Intersymbol Interference[S].
[11]馬雯.連續相位調制信號的功率譜及帶寬特性研究[J].現代電子技術,2010(5):39-41.
[12]趙彥惠.基于相位累加實現GMSK調制的技術分析[J].無線電工程,2013,43(3):20-23.
[13]鄭海榮.多調制指數連續相位調制解調算法的研究[D].哈爾濱:哈爾濱工業大學,2012:16-45.
[14]楊允軍,武傳華.用MATLAB實現GMSK信號的產生與解調[J].無線電工程,2005,35(9):58-60.
[15]陳敬喬.一種新的GMSK調制器的設計與實現方法[J].無線電工程,2014,44(7):79-82.
Spectrum Analysis and Demodulation Algorithm of M-ary GMSK
LI Chun-teng,ZHANG Shu-xia,LI Chong-yuan
(Electronic Engineering College,Naval University of Engineering,Wuhan Hubei 430033,China)
M-ary GMSK has a large advantage in spectrum efficiency,which is very important for improving the communication efficiency.Based on the signal spectrum of binary GMSK,the signal spectrum of M-ary GMSK is introduced and compared with binary GMSK,the generation algorithm of M-ary GMSK and demodulation methods are studied with the help of binary algorithm.A suboptimal maximum likelihood ratio demodulation method for M-ary GMSK is proposed.The simulation results show that the performance of this method has good performance in BER.
multi-ary;GMSK;spectrum;demodulation method
10.3969/j.issn.1003-3114.2016.05.10
引用格式:李春騰,張曙霞,李崇遠.多進制GMSK頻譜分析及解調算法[J].無線電通信技術,2016,42(5):38-41.
2016-05-20
李春騰(1992—),男,碩士研究生,主要研究方向:通信理論與技術。張曙霞(1968—),女,副教授,主要研究方向:信息網絡信號處理。
TP391.4
A
1003-3114(2016)05-38-4

