最小熵反褶積的數學形態法在滾動軸承故障特征提取中的應用
龔廷愷 袁曉輝 王細洋
1.華中科技大學,武漢,430074 2.南昌航空大學,南昌,330063
?
最小熵反褶積的數學形態法在滾動軸承故障特征提取中的應用
龔廷愷1,2袁曉輝1王細洋2
1.華中科技大學,武漢,4300742.南昌航空大學,南昌,330063
針對強噪聲背景下滾動軸承故障特征提取,提出了基于最小熵反褶積的數學形態法。該方法先應用最小熵反褶積算法加強信號中的沖擊特性,再利用數學形態法進行故障特征提取,其中選取具有雙向脈沖提取能力的DIF濾波器作為形態算子,并以峭度值作為結構元素長度選取依據。仿真信號和滾動軸承的內外故障實例分析表明該方法具有較好的特征提取效果。通過對比發現:最小熵反褶積算法能夠增大信號中峭度值,有效加強信號脈沖特性。
最小熵反褶積;數學形態;故障診斷;滾動軸承
0 引言
滾動軸承是旋轉機械中最常用的通用零部件之一,同時也是最易損的零件。根據統計,旋轉機械的故障中有30%是由軸承故障引起的,因此它的工作狀態對機器運行具有巨大的影響[1]。當故障點出現在軸承的內外圈及滾動體上時,周期性脈沖會產生。而且這些脈沖信號的頻寬范圍常常覆蓋了軸承和機械系統固有振動頻率,易引起軸承甚至機械系統的共振,導致機器振動和產生噪聲,甚至損壞。因此這些沖擊脈沖的成功提取成為軸承故障診斷的一種有效方法。
對于這些沖擊脈沖性的振動信號分析有很多方法,如局部特征分解、經驗模態分解和小波變換等[2-6]。相比前述方法,一種非線性的數學形態技術近來得到了廣泛關注。文獻[7]應用形態閉算子作為形態算子,以0.6倍的脈沖周期作為結構元素長度,成功提取出了軸承內外圈故障。但這種方法在選取結構元素長度時需要依賴經驗知識。為了克服這種缺陷,Dong等[8]提出了一種基于信噪比的改進形態分析方法。然而,在強噪聲背景下形態方法所能提取出的故障形態特征,即脈沖沖擊特性是非常有限的。因此在形態方法處理前,希望通過一種方法能夠簡化信號,突出信號中的沖擊特性,這樣形態方法就能提取出更多的故障形態特征,便于故障診斷。因此,基于上述考慮本文提出了一種基于最小熵反褶積的數學形態法(mathematical morphology based on minimum entropy deconvolution, MMBMED),并應用于故障軸承的振動信號特征提取中。該方法通過最小熵反褶積(minimum eneropy deconvolution, MED)方法進行預處理,而后應用數學形態方法提取故障特征,選取具有雙向脈沖提取能力的DIF濾波器作為形態算子,結構元素長度的確定通過峭度作為選取原則。仿真信號和滾動軸承內外圈故障分析表明,基于最小熵反褶積的數學形態方法具有較好的故障特征提取效果。
1 相關理論
1.1數學形態法
數學形態學的基本思想是用結構簡單、緊湊的結構元素去量度和提取圖像中的對應形狀,以達到對圖像分析和識別的目的。形態學的非線性特性可以簡化圖像,在保持圖像本質基礎上除去噪聲部分,最初是作為圖像處理工具的,后來才發展到一維信號處理。
數學形態學中包含4個基本形態運算算子,即膨脹算子、腐蝕算子、開算子和關算子。它們的定義分別如下:
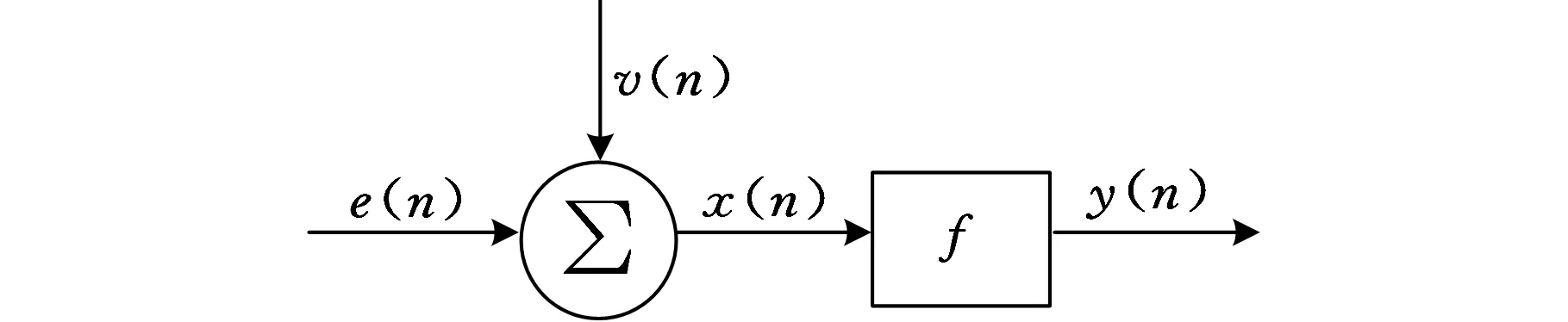
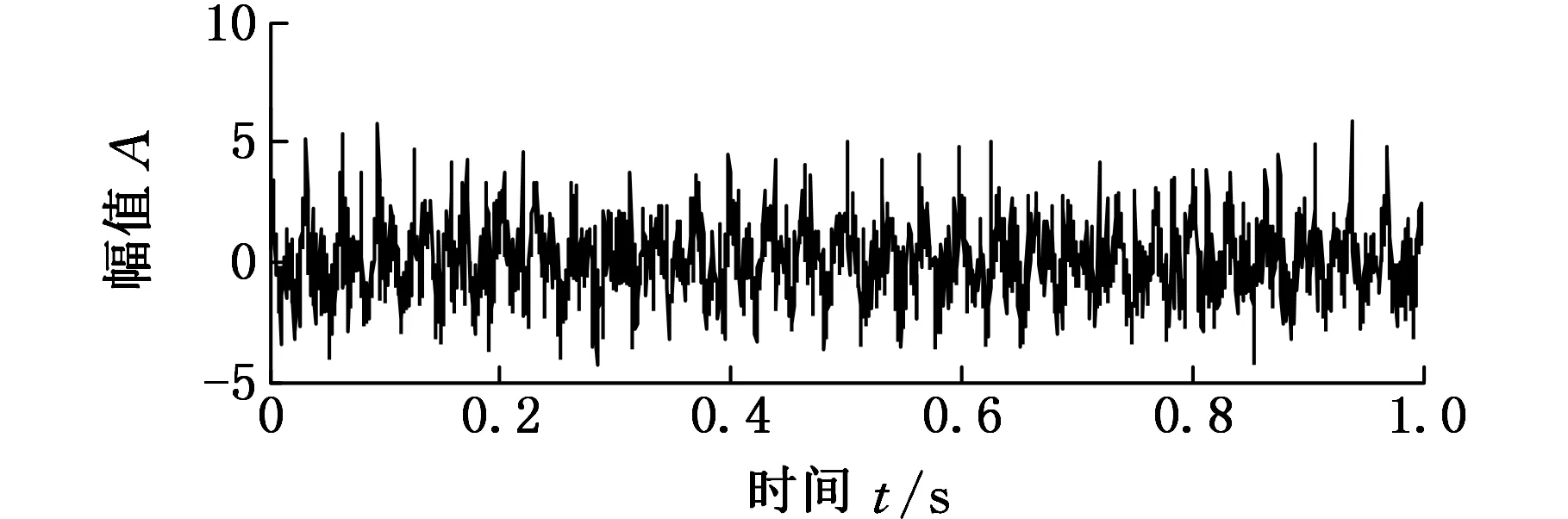
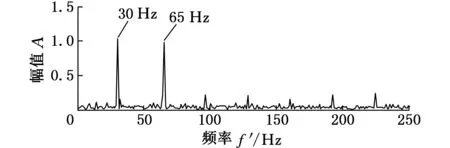
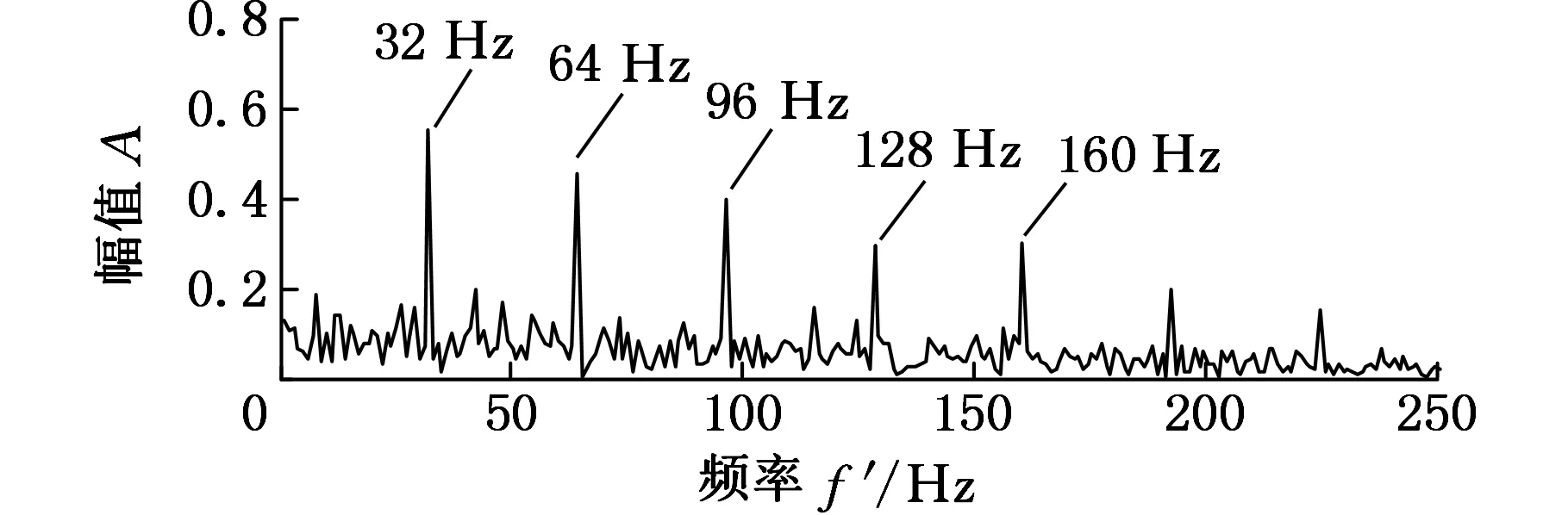
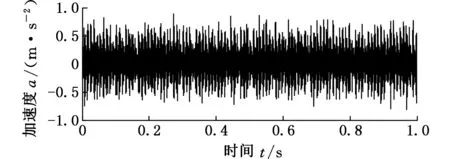
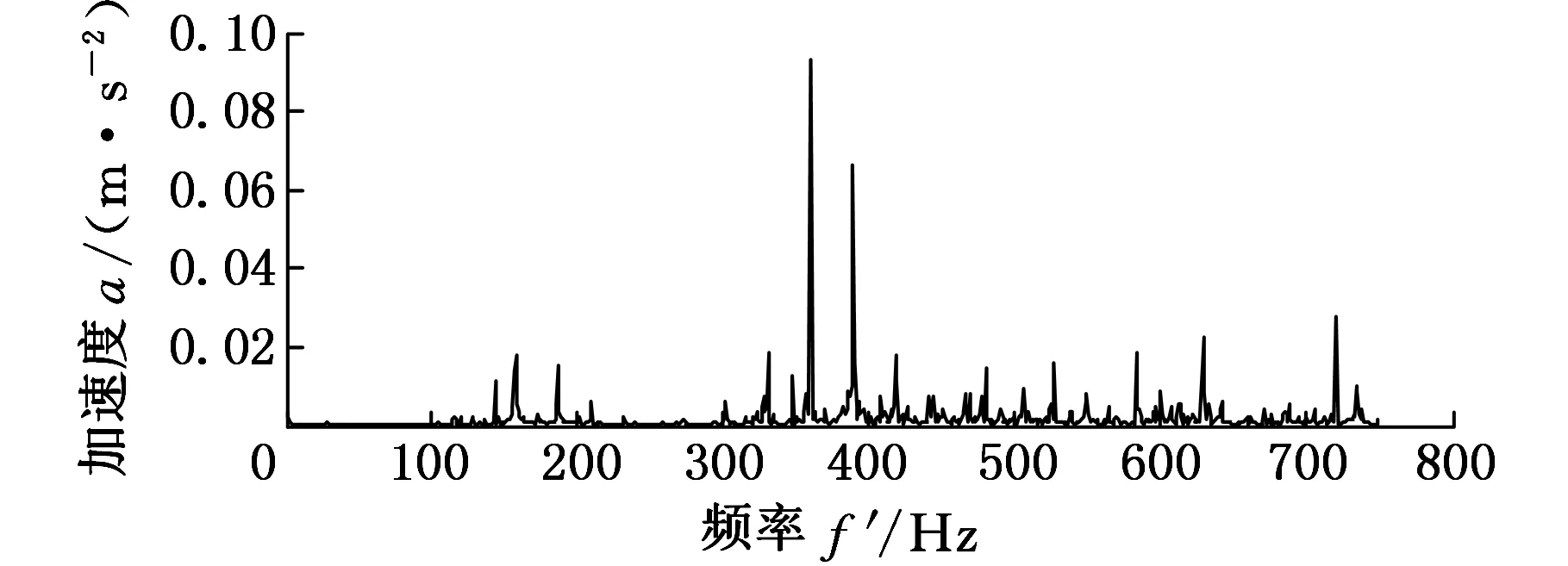
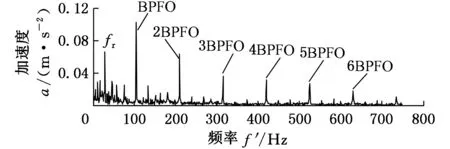
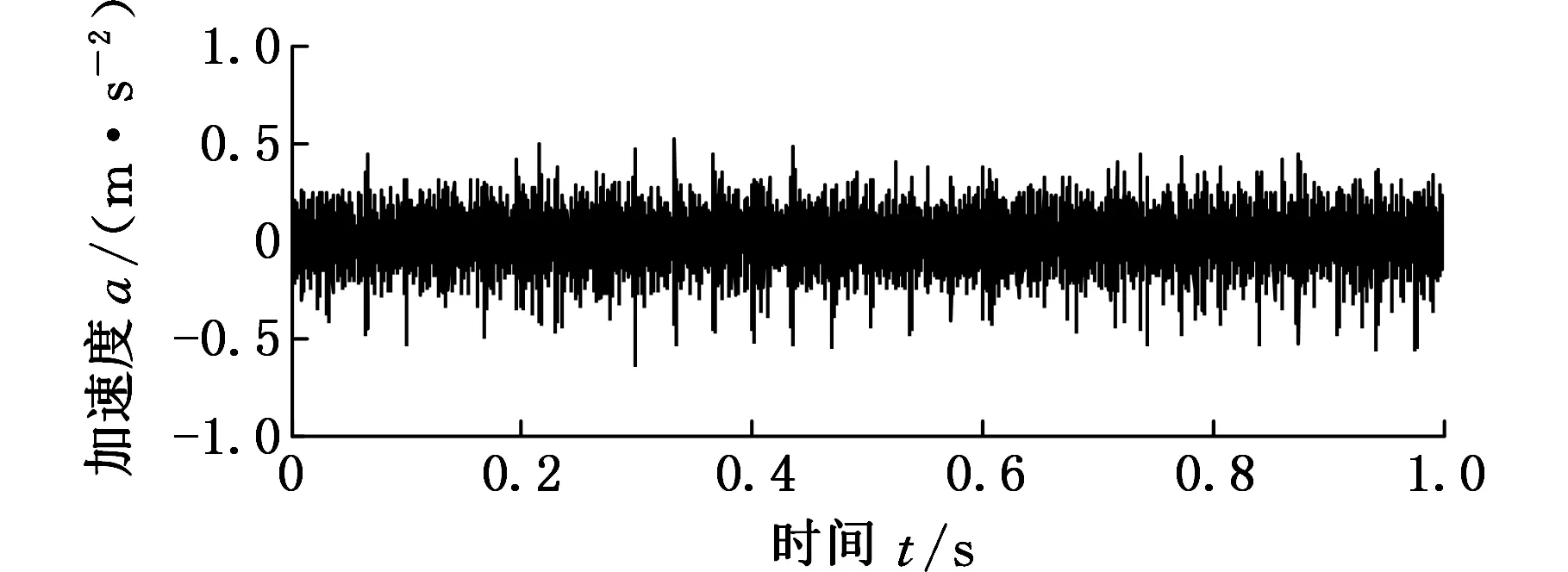
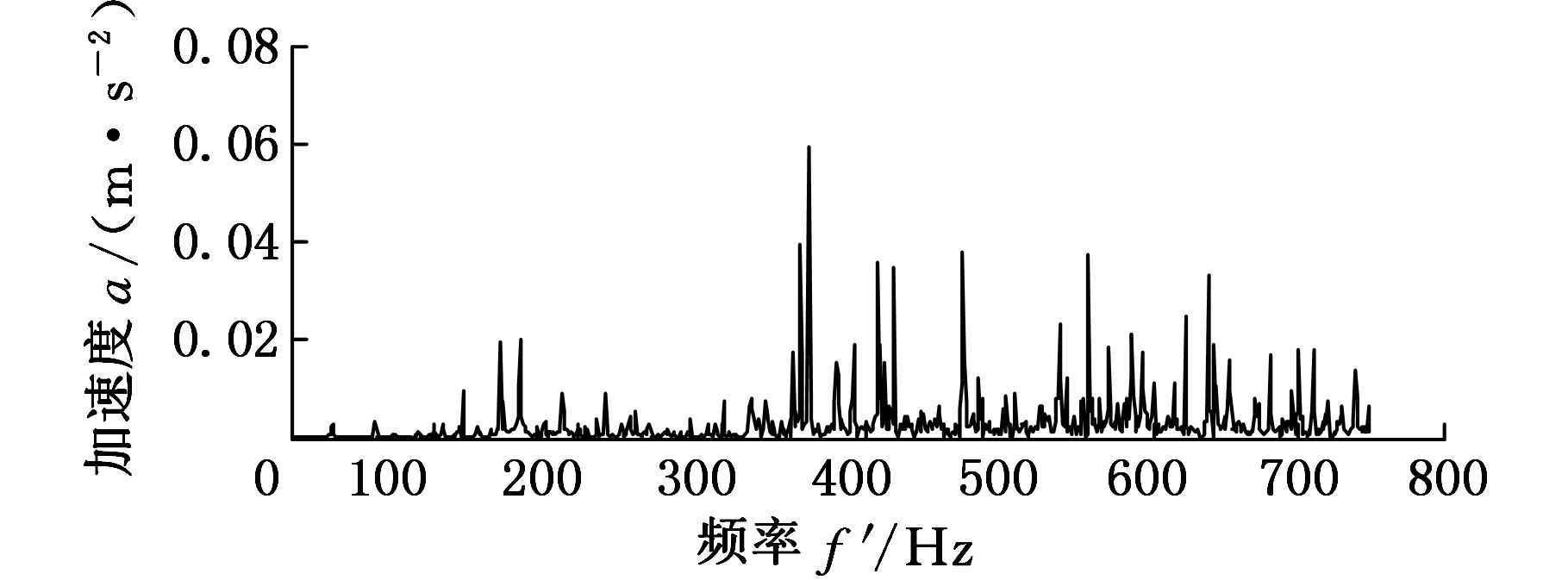
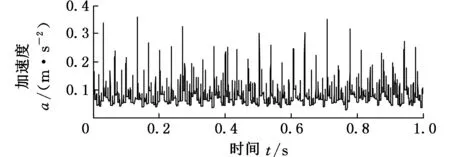
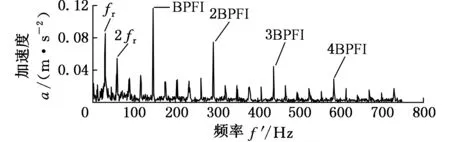
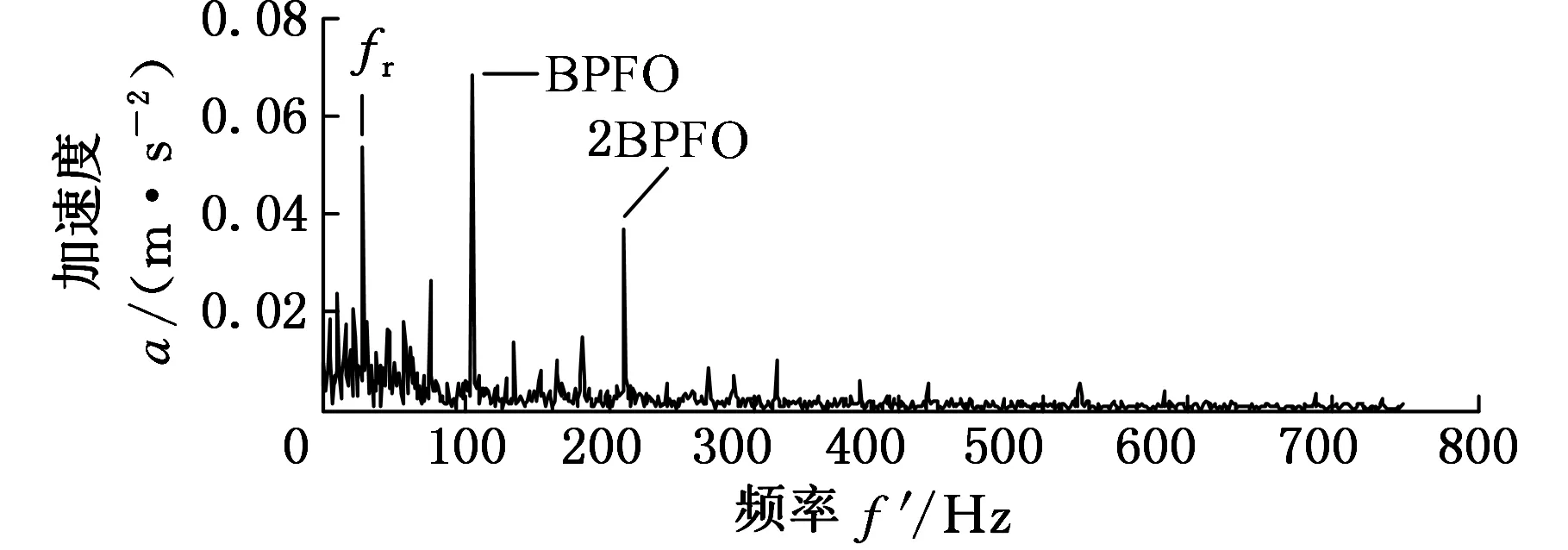
設f(n)為一維多值信號,s(n)為結構元素。H、K分別為f(n)和s(n)的定義域,H=(0,1,…,n-1),K=(0,1,…,m-1),且m (f⊕s)(n)=min(f(n-m)+s(n)) (1) m∈{0,1,…,M-1} (fΘs)(n)=min(f(n+m)-s(n)) (2) m∈{0,1,…M-1} 根據上述定義,形態開運算和形態閉運算的定義分別為 (3) (f?s)(n)=(f⊕sΘs)(n) (4) Nikolaou等[7]通過分析發現4種形態算子對脈沖信號的作用不同。如腐蝕運算對負脈沖具有平滑作用,會減少脈沖信號中的正脈沖部分。膨脹運算具有和腐蝕運算相反的效果。閉算子能夠保留信號中的正脈沖信號,開算子能夠保留信號中的負脈沖信號。顯然,實際應用中很難得到正負脈沖的先驗知識。因此,常常用4個基本算子的算術組合作為新的形態算子。例如,形態閉和開的差分運算得到的DIF(differencefilter)算子,其數學定義如下式所示: (5) 該算子具有同時提取正負脈沖信號的特性,因此具有較好的脈沖提取能力。 1.2最小熵反褶積算法 Wiggins[9]首次提出了MED的概念,并應用在地震信號處理當中。求取MED是指尋求一個反轉濾波器的最優系數集合,使得所恢復的輸出信號具有最大峭度。因為峭度是一個對故障敏感的因子,反映了信號中的峰值(即脈沖屬性),增大信號峭度值有助于軸承中的故障診斷。 圖1說明了MED算法原理。信號e(n)通過結構濾波器后的輸出和噪聲v(n)共同作為一個反轉濾波器 f 的輸入,輸出為y(n)。為了處理后有更好的效果,我們希望反轉濾波器f的輸出y(n)與最初的輸入信號e(n)盡可能相似。雖然系統輸入e(n)是未知的,但希望這些就是脈沖序列。Endo等[10]總結了MED方法具體過程: 圖1 MED算法原理 (1)最小熵算法為長度L的反轉濾波器 f找到一個系數集合,優化輸出信號y(n)的峭度: (6) 其中,[·]表示信號為離散信號。 (2)反轉濾波器的卷積表達式為 (7) (3)當目標函數(式(6))出現最大峭度值時,即 (8) (4)對式(7)兩邊求導可得 (9) (5)由式(7)和式(9)可將式(8)寫成: (10) 式(10)寫成矩陣形式如下: b=Af (11) 式中,A為輸出信號y(n)的自相關矩陣;b為濾波器的輸出立方與輸入信號的互相關加權和;f為反轉濾波器系數矩陣。 由式(11)通過迭代計算可以計算出反轉濾波器系數: f=A-1b (12) 由以上分析可以歸納出最小熵遞歸迭代算法步驟如下: (1)初始化反轉濾波器的系數,設定初始狀態f(0)中元素全為1; (2)通過輸出信號x(0)和反轉濾波器初始值f(0)(按式(7))計算y(0); (3)通過y(0)和x(0)(按式(11))計算列矢量b(1)(b(1)為第一次計算b的結果); (4)計算得到濾波器系數矩陣f(1)=A-1b(1); (5)計算預設定誤差。如果誤差小于設定值,結束計算。否則,返回步驟(3)。 仿真信號由諧波信號、脈沖信號和噪聲三個信號復合構成,其數學表達式如下: x(t)=x1+x2+x3 (13) 其中,諧波信號x1=cos(60t)+cos(130t);x2為周期為32 Hz的指數衰減序列,該信號在一個周期內的衰減函數為e-10tsin(10t);x3為均值為0,標準偏差為1的高斯白噪聲。采樣頻率fs為2048 Hz,采樣時間為1 s。圖2為仿真信號的時域圖和頻譜圖。在圖2b中脈沖特征頻率32 Hz、64 Hz等成分由于諧波信號和噪聲抑制,沒有被提取出來,因此采用建議方法進行分析。新方法處理過程為:①先采用MED方法預處理;②通過數學形態法提取特征,以式(5)中的DIF算子作為形態算子,選擇扁平型高度為0的結構元素。對于其長度,本文以脈沖重復周期T的0.1倍為間隔,構造9個不同長度的結構元素,即 {0.1T,0.2T,0.3T,0.4T,0.5T,0.6T,0.7T,0.8T,0.9T},分別計算9個不同長度的峭度值,最后選取最大峭度的長度作為結構元素長度。 (a)時域圖 (b)頻譜圖圖2 仿真信號 仿真信號經過MED處理后,繼續進行數學形態分析。計算9個不同長度的結構元素,發現長度為0.1T時的峭度值7.7879為最大,因此長度選擇0.1T,相應結果的頻譜圖見圖3a。從圖3a中發現脈沖特征頻率32 Hz,以及它的諧波成分(64~160 Hz) 都被提取出來了,諧波成分和噪聲得到了較好的抑制。特征提取效果說明最小熵反褶積和數學形態法相結合能夠有效提取出脈沖特征成分,較好地抑制噪聲。 為了說明MED方法的作用,仿真信號將直接運用新方法的第二步進行處理與對比。計算發現在0.1T時的峭度值只有4.2503,其結果頻譜圖見圖3b。圖中只發現了幾個脈沖特征頻率(64 Hz,96 Hz,128 Hz和160 Hz)。與圖3a對比可知:仿真信號未經過MED預處理,結構元素長度在0.1T時峭度值從4.2503增大到7.7879,峭度值明顯增大。圖3b雖然提取出了幾個脈沖特征頻率,但它們周圍的噪聲較大,而且脈沖特征頻率32 Hz沒有提取出來。因此通過這個對比說明MED算法能夠優化信號的峭度,加強信號的脈沖特性。 (a)有MED處理 (b)無MED處理圖3 仿真信號頻譜圖對比 3.1滾動軸承外圈故障分析 實例分析的數據來自于美國凱西西楚大學軸承試驗中心。實驗中外圈故障測試軸承為SKF6205-2RSJEMSKF深溝球軸承。采樣頻率為12kHz,采樣點數為12288。轉速為1750r/min,由計算可得外圈故障通過頻率(theballpassingfrequencyouterrace,BPFO)約為105.1Hz。外圈故障原始振動信號如圖4a所示。在圖4b中BPFO等特征成分沒有顯現,因此采用本文方法處理。 (a)時域圖 (b)頻譜圖圖4 外圈故障原始信號 外圈故障信號經MED處理后,計算發現當結構元素長度為0.9T時峭度值達到最大,為8.2639,因此結構元素長度為0.9T,結果如圖5所示。圖5b中清楚提取出了BPFO和它的幾個諧波成分(2BPFO,3BPFO,4BPFO,5BPFO和6BPFO)。此外轉速fr也被找到。上述分析表明新方法有效診斷出了滾動軸承外圈故障。 (a)時域圖 (b)頻譜圖圖5 外圈故障的新方法分析結果 3.2滾動軸承內圈故障分析 為了進一步說明新方法對軸承內圈故障的有效性,以一個內圈故障為例進行分析。測試軸承型號為6203-2RSJEMSKF。采樣頻率為12kHz,采樣點數為12 288,轉速為1772r/min。計算可知外圈故障通過頻率(theballpassingfrequencyinnerrace,BPFI)約為146Hz。內圈故障原始振動信號如圖6a所示,其頻普圖如圖6b所示。 (a)時域圖 (b)頻譜圖圖6 內圈故障原始信號 新方法處理后計算發現結構元素長度為0.6T時峭度值最大,為14.7514,因此結構元素長度為0.6T,相應結果如圖7所示。在圖7b頻譜圖中,內圈故障特征頻率BPFI成為了主要成分,它的三個諧波成分(2BPFI,3BPFI和4BPFI)也能夠識別出來,同時還能發現轉速 fr和它的2倍頻成分。此外特征頻率BPFI及它的諧波兩側還清晰找到了豐富的邊頻帶,即頻率成分為146κ±30i(其中,i=1,2;κ=1,2,3,4)。因此,這些結果說明新方法對滾動軸承內圈故障的特征提取也是有效的。 (a)時域圖 (b)頻譜圖圖7 內圈故障的新方法分析結果 3.3有無最小熵反褶積方法的軸承內外圈故障對比 與仿真信號中的對比相同,軸承內外圈故障原始振動信號直接采用數學形態法處理,外圈和內圈故障時結構元素長度仍然是0.9T(峭度值2.9685)和0.6T(峭度值6.0521),相應頻譜圖分別為圖8a和圖8b。圖8a外圈故障中只有BPFO和2BPFO被提取出來。圖8b內圈故障中,也只有BPFI和2BPFI被識別,而且特征頻率兩側的邊頻帶也未發現。與圖5b和圖7b相比:經過MED方法處理后,外圈故障時峭度值從2.9685增大到8.2639,所提取BPFO的諧波成分更多(從BPFO~6BPFO)。內圈故障時峭度值從6.0521增大到14.7514,所提取BPFI的諧波成分更多(從BPFI~4BPFO),以及它們兩側邊頻帶也較為明顯。因此,事實說明MED算法的峭度值增大效果明顯,有效加強了軸承內圈故障信號的脈沖特征,特征提取效果更好。 (a)外圈無MED分析 (b)內圈無MED分析圖8 軸承外圈和內圈故障時的頻譜圖對比 為了提取出強噪聲背景下滾動軸承內外圈故障的特征頻率,提出了基于最小熵反褶積的數學形態法。新方法利用MED方法進行預處理,以提高原始信號峭度值,加強故障的沖擊特性。然后運用數學形態方法提取故障特征。選取了DIF濾波器作為形態算子,結構元素長度以9個不同長度中峭度值作為選取依據。通過仿真信號和滾動軸承內外圈故障分析說明新方法能夠提取出豐富的故障特征。通過對比發現最小熵反褶積使得信號峭度值增大明顯,軸承故障信號沖擊特征得到了加強,故障特征提取效果明顯。 [1]McFaddenPD,SmithJD.VibrationMonitoringofRollingElementBearingsbytheHigh-frequencyResonanceTechnique—AReview[J].TribologyInternational, 1984, 17:3-10. [2]GeorgoulasG,LoutasT,StyliosCD,etal.BearingFaultDetectionBasedonHybridEnsembleDetectorandEmpiricalModeDecomposition[J].MechanicalSystemsandSignalProcessing, 2013, 41:510-525. [3]GuoW,TsePW,ANovelSignalCompressionMethodBasedonOptimalEnsembleEmpiricalModeDecompositionforBearingVibrationSignals[J].JournalofSoundandVibration, 2013, 332:423-441. [4]QiuH,LeeJ,LinJ,etal,WaveletFilter-basedWeakSignatureDetectionMethodandItsApplicationonRollingElementBearingPrognostics[J].JournalofSoundandVibration, 2006,289:1066-1090. [5]楊宇, 程軍圣. 基于LCD降噪和VPMCD的滾動軸承故障診斷方法[J]. 中國機械工程, 2013, 24(24):3338-3344. YangYu,ChengJunsheng.ARollingBearingFaultDiagnosisMethodBasedonLCDDenoisingandVPMCD[J].ChinaMechanicalEngineering, 2013, 24(24):3338-3344. [7]NikolaouNG,AntoniadisIA.ApplicationofMorphologicalOperatorsasEnvelopeExtractorsforImpulsive-typePerodicSignals[J].MechanicalSystemsandSignalProcessing, 2003,17:1147-1162. [8]DongY,LiaoM,ZhangX,etal.FaultsDiagnosisofRollingElementBearingsBasedonModifiedMorphologicalMethod[J].MechanicalSystemsandSignalProcessing, 2011,25:1276-1286. [9]WigginsRA.MinimumEntropyDeconvolution[J].Geoexploration, 1978,16:21-35. [10]EndoH,RandallR.EnhancementofAutoregressiveModelBasedGearToothFaultDetectionTechniquebytheUseofMinimumEntropyDeconvolutionFilter[J].MechanicalSystemsandSignalProcessing, 2007,21:906-919. (編輯王艷麗) Applications of Mathematical Morphology Method to Fault Feature Extraction of Rolling Bearings Based on Minimum Entropy Deconvolution Gong Tingkai1,2Yuan Xiaohui1Wang Xiyang2 1.Huazhong University of Science and Technology, Wuhan,430074 2.Nanchang Hangkong University, Nanchang, 330063 Aiming at the extractions of fault features of rolling bearings under the strong noise background, a novel method, called mathematical morphology based on minimum entropy deconvolution (MMBMED) was proposed herein. In this method, MED was first introduced to enhance the impact behaviors of the signals. And the fault characteristics of defective bearings were extracted by MM method, where the DIF filter with catching the bidirectional pulses was adopted as morphological operator, and kurtosis was employed as the criterion to the length selection of structural elements. The effectiveness of the new method was validated by both of simulation signals and vibration signals of rolling bearings with the outer and inner race faults. Finally, the results disclose that MED is effective to increase signal kurtosis and to strengthen the impulsive characteristics. minimum entropy deconvolution(MED); mathematical morphology(MM); fault diagnosis; rolling bearing 2015-07-13 國家自然科學基金資助項目(51379080,AA201406168) TH 165;TN911 10.3969/j.issn.1004-132X.2016.18.009 龔廷愷,男, 1977年生。華中科技大學數字化水電工程學院博士,南昌航空大學飛行器工程學院講師。主要研究方向為旋轉機械故障診斷及信號處理。袁曉輝,男, 1971年生。華中科技大學數字化水電工程學院教授、博士研究生導師。王細洋,男,1967年生。南昌航空大學飛行器工程學院教授。

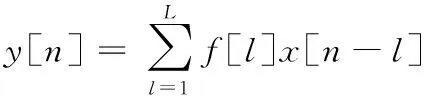
2 信號仿真

3 實例分析


4 結語