基于部分可觀察馬爾可夫決策過程的機電裝備動態可靠性評價方法

張紅旗　邵曉東　胡祥濤

1.西安電子科技大學,西安,7100712.中國電子科技集團公司第三十八研究所,合肥,230088

?

基于部分可觀察馬爾可夫決策過程的機電裝備動態可靠性評價方法

張紅旗1,2邵曉東1胡祥濤2

1.西安電子科技大學,西安,7100712.中國電子科技集團公司第三十八研究所,合肥,230088

針對機電裝備運行維護問題，提出了基于部分可觀察馬爾可夫決策過程(POMDP)理論的動態可靠性評價方法。該方法將可靠性動態演變看成POMDP問題，通過不完全觀測到的設備運行信息(如噪聲、溫度、壓力等)，對可靠性狀態進行估計，同時分析不同的維修行為對可靠性水平的影響規律，構建了基于狀態轉移的動態可靠性評價模型。然后，提出了以最小化維修成本費用和潛在故障危害為目標的維護策略制定方法，并通過案例分析驗證了該方法的有效性，實現了機電裝備動態可靠性的有效評價與維護策略的科學制訂。

可靠性評價；維護策略;POMDP；機電裝備

0　引言

機電裝備集成了電、機、液等多種技術，其失效機理相當復雜，導致其可靠性難以評價[1-3]。一方面缺少有效的基礎數據，可靠性預計結果誤差較大；另一方面，在環境載荷持續作用下系統性能逐漸劣化，呈現出多態、時變和相關特性，常規的可靠性分析手段存在很多與工程不相適應的地方。因此，如何實時描述和獲得機電裝備運行狀態和可靠性水平，即所謂的動態可靠性評價問題，是復雜機電裝備運行維護過程中難題之一。

針對上述難題，國內外學者分別采用了動態貝葉斯網絡(dynamic bayesian network，DBN)理論、部分可觀察馬爾可夫決策過程(partially observable Markov decision processes, POMDP)、Petri網等理論開展了廣泛的研究[4-10]。其中，POMDP理論因能描述不確定環境下序貫決策問題而受到青睞，在機電裝備運行狀態估計、維修策略制訂等領域中獲得了廣泛研究。劉繁茂等[1]利用POMDP理論，在基于設備狀態的視情維修模式下，提出了以最小化折扣費用為目標函數的設備檢測和維修的聯合決策方法。黃飛騰等[2]基于系統的馬爾可夫性假設，對系統狀態進行適當的離散化處理，利用狀態轉移方法來描述系統的動態隨機過程，再建立離散動態事件樹求得系統故障概率。尚永爽等[11]針對部分可觀測信息條件下的退化系統，提出利用部分可觀測馬爾可夫決策過程模型解決系統視情維修問題。實例研究表明，該方法可為保障人員提供科學的維修決策依據。但是，目前的大多數研究都存在模型過于簡單、考慮因素單一等問題，與復雜環境下設備維修需求尚有差距。另外，由于POMDP存在“維度災”問題，缺少有效的求解算法，也限制了該理論在機電設備運行維護中的工程應用。

本文將機電裝備的動態可靠性問題看成部分可觀察馬爾可夫決策過程，通過不完全觀測到的設備運行信息(如噪聲、溫度、壓力、振動水平等),對機電裝備進行動態可靠性評價，提出以最小化維修成本費用和潛在故障代價為目標函數的設備維護策略制訂方法，為機電設備可靠性動態評價和維修策略制訂提供有效途徑。

1　POMDP概述

POMDP的基本框架可以表示為6元數組[12-13]。其中，S為有限狀態集，一般采用離散形式表示，如S={1,2,…,n}，n代表狀態空間的規模；A為有限行動集，通常表示為A={1,2,…,m}，m代表行動空間的規模；T為狀態轉移函數，S×A→S′表示在狀態s下執行行動a后，狀態轉移為s′的概率為P(s′|s,a)，也記為Ta(s,s′)或T(s,a,s′)；R為立即收益函數，S×A→R意為在狀態s下執行行動a后期望得到的立即收益，也稱作報酬函數，用R(s,a)表示；O為有限觀測集，通常表示為O={1,2,…,l}，l代表狀態空間的規模；Ω為觀測函數，表示執行行動a后，狀態為s′時觀測到o的概率，即P(o|s′,a)，也記為Ω(s′,a,o)。

1.1信念狀態(BeliefState)

圖1表示POMDP模型中的決策過程。由圖1可知，信念狀態是行動決策的直接依據，信念狀態的轉移具有馬爾可夫性[14-15]。信念狀態b′可以用貝葉斯公式進行更新[12-13]，具體過程如下：

(1)

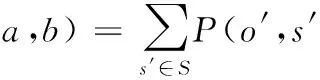
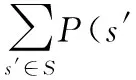
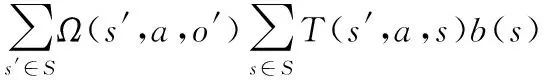
(2)

式(2)為歸一化因子。根據轉移函數T及觀測函數Ω，就可以實現信念狀態的轉移更新。

圖1　POMDP模型中決策過程示意圖

1.2值函數

為了尋求最優行動策略，需要確定值函數。策略表示信念狀態空間到行動集的映射：a=π(b)。對于一個初始狀態s，按照策略執行動作得到的期望收益為[12-13]

V(s)=R(s,a)+γVfuture

(3)

(4)

其中，Vfuture為執行動作a之后的潛在長期收益；γ為折扣值，表示相對立即收益R存在一個時間折扣。

按照式(3)和式(4)，初始信念狀態b的最優值函數和最優策略可以表示為

(5)

(6)

t∈T

求解POMDP問題，就是要計算整個信念狀態空間中每個信念狀態上的最優值函數。受“維度災”的影響，目前常采用的算法是基于點的值迭代算法(point-based value iteration, PBVI)。PBVI算法屬于近似算法，只在信念狀態空間部分點上進行計算，由兩個步驟組成：①在給定的信念點集上更新值函數；②擴充信念點集。兩個步驟交替執行，直到值函數收斂或者滿足終止條件為止。

2　動態可靠性評價模型

機電裝備的可靠性評價和維護，需要綜合考慮裝備的運行狀態、資源和費用耦合問題。例如，設備某個組件的振動幅值隨著時間而變化，反映了它可靠性水平在變化，維修策略也要相應變化。這些時變的因素需要綜合在一起考慮，從而決定可靠性水平怎么樣，何時維修，怎么維修，目標是在設備的可靠性和可用性可以接受的水平下，最小化裝備檢測維修費用和潛在故障代價。

2.1狀態集、觀測集與行動集

按照上節所述，POMDP模型需要確定系統的狀態集、觀測集與行動集。為了實現對機電裝備可靠性評價，本文將可靠性水平看成系統狀態。并假定在復雜工作環境下，系統可靠性水平的動態演變符合POMDP理論。

一般情況下，可靠性屬于隱藏狀態，需要借助觀察或監測信息對其合理估計。工程中，一般是依賴設備的振動水平、噪聲水平、溫度等可觀測信息來評估設備可靠性水平。比如，噪聲水平長期維持在高水平，說明結構內部可能存在磨損等故障源，可靠性水平降低，需要進行拆機檢修。POMDP 模型的觀測集可以集成機器的性能參數和每個檢測行動取得的多種診斷信息, 如某個時間噪聲水平和振動信號的幅值。

不同可靠性水平需要采取不同的維修策略。設備如果高可靠，就只需簡單維護；反之，則需要大修。不同的維修行為用于構建行動集，如維護、置換組件、置換機器、機器的連續運行或者檢測等。

綜上所述，假定某個系統的壽命歷史能夠模擬成一個離散時間的有限狀態的馬爾可夫過程，下面給出基于POMDP的動態可靠性評價模型定義：

狀態集S={1, 2, 3, 4, 5}，分別對應機電裝備高可靠、可靠、亞可靠、次可靠、不可靠。

行動集A={1, 2, 3, 4}，分別對應簡單保養、普通維護、小修、大修。

假設一個機電系統有k個觀測量，分別為O1、O2…、Ok，將每個觀測量按照大小離散為5個水平，對應“低”“中下”“中”“中上”“高”。則觀測集定義為：Oi={1, 2, 3, 4, 5}，i=1,2,…,k。

2.2轉移函數和觀測函數

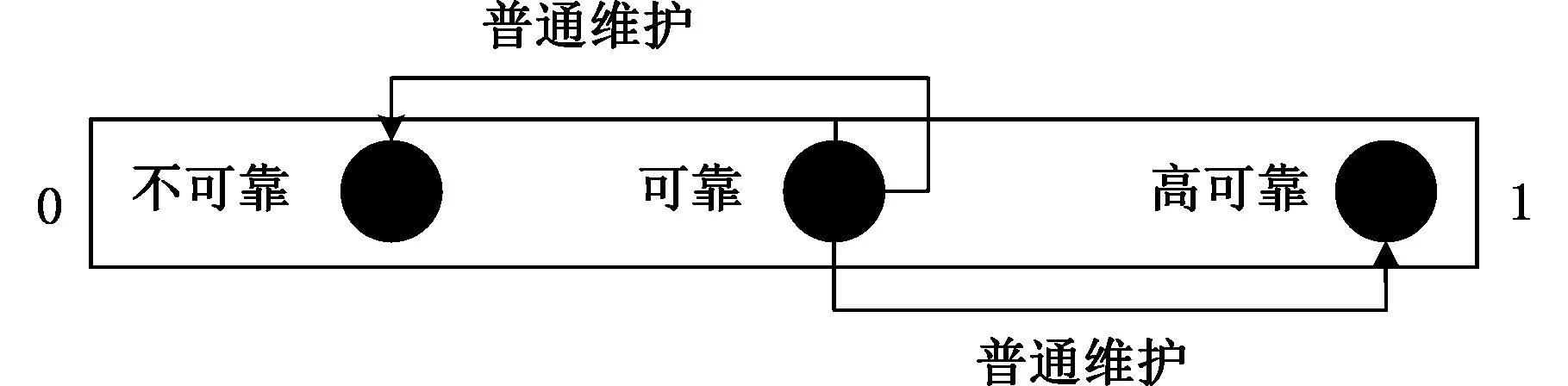
圖2　可靠性水平狀態轉移示意圖

狀態轉移函數Ta(s,s′)如圖2所示，即假定當前系統狀態為可靠，采取的行動集——維修策略是普通維護，則下一時刻系統狀態(不可靠、可靠、高可靠)以一定概率發生轉移。本質上，狀態轉移函數屬于條件概率范疇，反映了維修行為對系統可靠性水平影響程度。大多數情況下，這種影響是正面的，但并不是完全百分之百的。因為設備固有的退化性質以及誤操作等不確定因素，導致維修不可能回到初始正常狀態。也就是說，即使采取了維修操作，設備的可靠性仍然是值得懷疑的。工程中，狀態轉移函數的確定需要依賴經驗知識，是人工維修行為的一種智能化過程。

系統的觀測函數Ω(s′,a,oi)=P(oi|s′,a)，表示執行行動a后進入下一個狀態s′時觀測到oi的概率。顯然觀測函數構建了裝備可靠性水平、觀測信息和維修行為之間的邏輯關系。即維修行為越合理，可靠性水平越高，觀測到的信息也是正向相關的。

由于系統有k個觀測信息，因而對應著k個觀測函數。按照式(1)，信念狀態由觀測函數和轉移函數共同決定和更新計算。因此，每個觀測函數會對應一個信念狀態，記為bi。本文通過加權方式，確定最終的信念狀態：

比較兩組患者Hb水平,術前差異無統計學意義(P>0.05),術后3d、7d時,研究組均高于對照組(P<0.05)。詳見下表2:

(7)

式中，ωi為加權系數，且∑ωi=1。

工程中，需要綜合各種觀測信息對機電裝備的可靠性水平作一個合理估計，不同的觀測信息會導致估計值不同。當觀測信息的可信度較高時，其權重自然要大些。同理，在根據式(4)和式(5)計算值函數時，首先分別計算不同觀測函數對應的值函數，再加權求總的值函數，這里不再贅述。

2.3值函數

一般來說，機電裝備有多個不同的維修和檢測方法，其費用和效果都不相同。不當的維修行為會導致成本升高，且設備達不到最優運行狀態。因此，合理的維修策略取決于每個時間點系統的可靠性水平。

本文綜合考慮了維修成本和潛在故障危害，定義評價函數如下：

R(s,a)=f(s)+g(a)

(8)

其中，f為潛在故障危害代價函數，表示系統在當前可靠性信念狀態下潛在的故障危害；g為維修成本函數，表示采取維修行為之后需付出的維修成本。將式(8)代入式(5)和式(6)，即可獲得最優維護策略。

3　案例分析

以某型號雷達天線旋轉系統為例，該系統由軸承、齒輪、旋轉軸、電機、傳感器等零部件組成，主要失效模式為旋轉運動部件的磨損、零部件的銹蝕卡死、結構疲勞變形、電機故障等。系統的可靠性水平可以通過噪聲水平和振動水平進行判斷，可靠性評價周期為1年。基于第2節所述，POMDP模型可以定義如下：

行動集定義為A= {1, 2, 3, 4}。其中，a=1表示簡單保養，如緊固螺釘、加潤滑、去銹漬等；a=2表示普通維護，需更換非關鍵件，如螺栓、線路、傳感器等；a=3表示小修，需對電機、驅動器、軸承等設備進行檢修；a=4表示大修，需更換關鍵件，如電機、軸承、齒輪等。

噪聲觀測集O1={1, 2, 3, 4, 5}。其中，o1=1表示低噪聲，設備運行正常；o1=2表示中低噪聲，設備存在潤滑不良或安裝松動；o1=3表示中噪聲，設備可能存在些微磨損、變形或安裝松動；o1=4表示中高噪聲，設備可能存在磨損或變形；o1=5表示高噪聲，設備可能存在較大磨損或變形。

振動觀測集O2={1, 2, 3, 4, 5}。其中，o2=1表示低振動水平，設備運行正常；o2=2表示中低振動水平，轉子些微不平衡、激勵載荷或負載些微異常；o2=3表示中等振動水平，轉子不平衡、激勵載荷或負載異常；o2=4表示中高振動水平，轉子較大不平衡、激勵載荷或負載較大異常；o2=5表示高振動水平，轉子嚴重不平衡、激勵載荷或負載嚴重異常。

根據工程經驗，假設狀態轉移函數和觀測函數分別如表1～表3所示。表1中，a=1表示只需進行簡單的日常保養，如果當前可靠性水平為高可靠(s=1)，下一時刻可靠性水平的5個狀態概率分別為0.99、0.01、0、0和0；如果當前可靠性水平為可靠(s=2)，下一時刻可靠性水平的5個狀態概率分別為0.05、0.75、0.20、0和0；如果當前可靠性水平為不可靠(s=5)，下一時刻可靠性水平的5個狀態概率分別為0、0、0、0.01和0.99。表2中噪聲觀測函數表示：如果當前設備是低噪聲水平(o1=1)，則當前可靠性水平的5個狀態概率分別為0.95、0.04、0.01、0和0；如果當前設備是一般噪聲水平(o1=3)，則當前可靠性水平的5個狀態概率分別為0.35、0.35、0.15、0.1和0.05；如果當前設備是高噪聲水平(o1=5)，則當前可靠性水平的5個狀態概率分別為0、0.05、0.1、0.25和0.6。類似地，表3中振動觀測函數表達了振動水平同機電裝備可靠性水平之間的概率關系。按照式(7)，假設振動和噪聲觀測函數的加權系數皆為0.5。

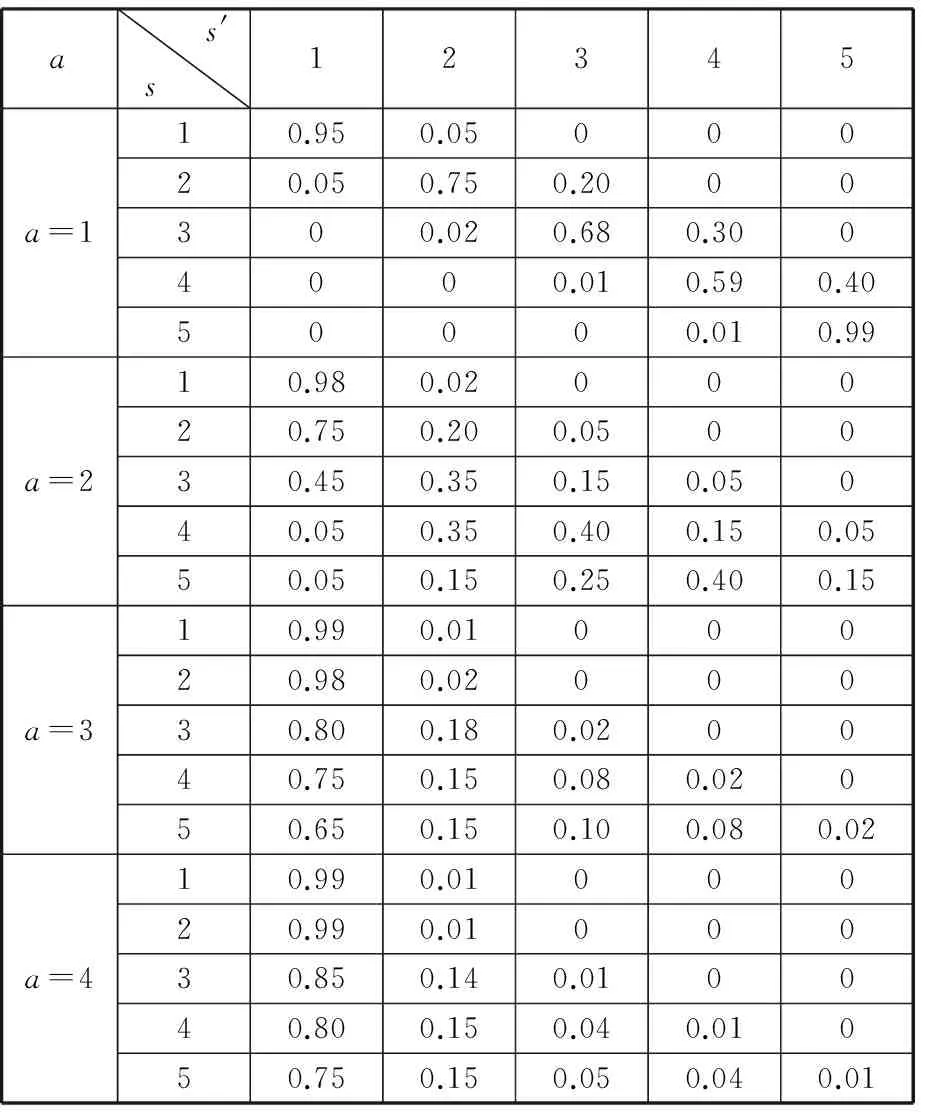
表1　狀態轉移函數

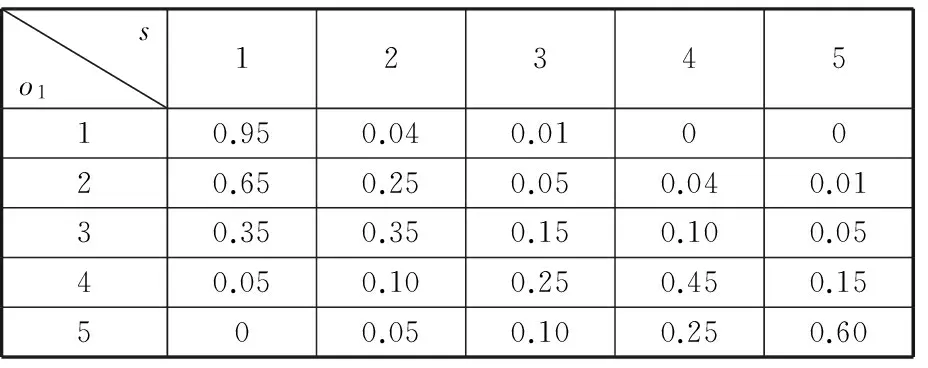
表2　噪聲觀測函數

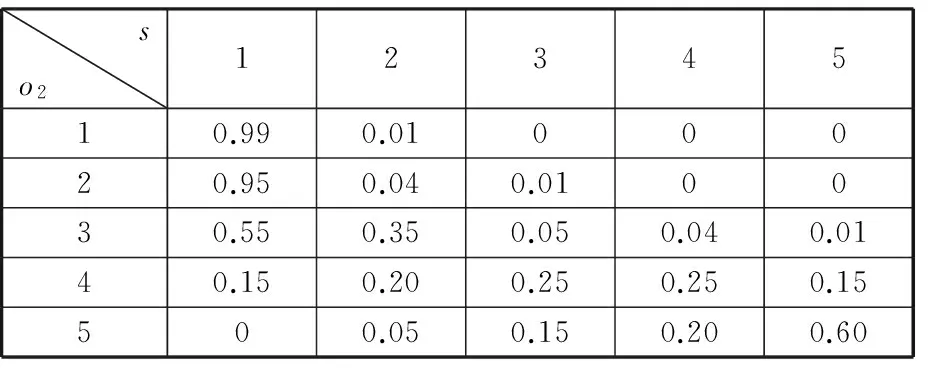
表3　振動觀測函數

評價函數定義如下：

R(s,a)=5s+1+10a

假設行動a分別為1、2、3、4的經濟成本分別為10、100、1000和10 000；故障危害的代價主要由可靠性水平決定，對應s分別為1、2、3、4、5，付出的代價分別為25、125、625、3125和15 625。

設初始信念狀態b(s)=(0.99,0.01,0,0,0)，將上述設置代入到式(5)～式(7)，可求得系統在不同信念狀態b下最佳維修策略。以可靠性水平s=5為例，描述如下：①b(s)≤0.05,a=1表示當前系統處在不可靠狀態的估計概率不大于0.05，采取日常保養策略；②0.050.45,a=4表示當前系統處在不可靠狀態的估計概率大于0.45，采取大修策略。

在這種維修策略下，該雷達天線旋轉系統可以持續工作18年。工程中，該雷達實際大修時間為服役15年后，表明本文提出的維修策略是合理的。

4　結語

本文針對機電裝備運行維護問題，提出了基于POMDP理論的動態可靠性評價和維護策略制訂方法。當機電裝備動態可靠性問題被看成不確定環境下序列決策問題時，POMDP模型可以幫助發現最優維護策略。在構建動態可靠性評價模型時，重點討論了狀態轉移函數、觀測函數和評價函數等POMDP模型中的幾個關鍵參數的定義。最后，針對某雷達旋轉系統線進行了案例分析，結果表明基于POMDP的動態可靠性評價和維護策略制訂方法是合理有效的，與工程實際情況相吻合。

然而，本文提出的動態可靠性評價和維護策略制訂方法，僅僅考慮了一種理想的變化情況，對系統動態可靠性問題作了一些必要的簡化。雖然模型具有一定的合理性和有效性，但是該模型仍然存在很多需要進一步改進的地方，比如細化狀態的表示、在模型中加入其他決策評價方法、更合理的轉移函數和觀測函數獲取方法、針對行動空間和觀察空間龐大的問題提出更高效的POMDP近似算法等。

[1]劉繁茂,朱海平,邵新宇,等.狀態不完全可觀條件下設備檢修策略研究[J].計算機集成制造系統,2009,15(8):1628-1632.

LiuFanmao,ZhuHaiping,ShaoXinyu,etal.InspectionandMaintenancePolicyofMachineBasedonPartiallyObservableMarkovDecisionProcesses[J].ComputerIntegratedManufacturingSystems, 2009, 15(8):1628-1632.

[2]黃飛騰,郁軍,肖航.基于Markov狀態轉移的動態可靠性分析[J].海軍工程大學學報,2002,14(6):80-83.

HuangFeiteng,YuJun,XiaoHang.DynamicReliabilityAnalysisBasedonMarkovStateTransition[J].JournalofNavalUniversityofEngineering, 2002, 14(6):80-83.

[3]SiuN.RiskAssessmentforDynamicSystems:anOverview[J].ReliabilityEngineeringandSystemSafety, 1994,43:43-73.

[4]EllisH,JiangMingxiang,CorotisRB.Inspection,Maintenance,andRepairwithPartialObservability[J].JournalofInfrastructureSystem, 1995, 1(2):92-99.

[5]CassandraAR.ASurveyofPOMDPApplications[C]//Proceedingsofthe3rdAnnualConferenceonUncertaintyinArtificialIntelligence(UAI-98).SanFrancisco,CA.,USA:MorganKaufmann, 1998:472-478.

[6]KuoY.OptimalAdaptiveControlPolicyforJointMachineMaintenanceandProductQualityControl[J].EuropeanJournalofOperationalResearch, 2006, 171(2):586-597.

[7]IvyJS,NembhardHB.AModelingApproachtoMaintenanceDecisionsUsingStatisticalQualityControlandOptimization[J].QualityandReliabilityEngineeringInternational, 2005, 21(4):355-366.

[8]HsuSP,ArapostathisA.SafetyControlofPartiallyObservedMDPswithApplicationstoMachineMaintenanceproblems[C]//ProceedingsofIEEEInternationalConferenceonSystems,ManandCybemetics.Hague,Netherlands:IEEE, 2004:261-265.

[9]胡祥濤,張紅旗,林寧,等.基于動態貝葉斯網絡的天線俯仰系統動態可靠性評估[J].電子機械工程,2014,30(6):22-26.

HuXiangtao,ZhangHongqi,LinNing,etal.ReliabilityAssessmentforAntennaPitchingSystemBasedonDynamicBayesianNetwork[J].Electro-mechanicalEngineering, 2014, 30(6):22-26.

[10]沈戈,蘇春,許映秋.基于Petri網理論的動態系統可靠性建模方法研究[J].機械工程與自動化,2006,30(2):1-3.

ShenGe,SuChun,XuYingqiu.ResearchonDynamicSystemReliabilityModelingMethodBasedonPetriNetTheory[J].MechanicalEngineering&Automation, 2006, 30(2):1-3.

[11]尚永爽,許愛強,李文海,等.部分可觀測信息條件下系統最佳檢修策略分析[J].系統工程與電子技術,2012,34(4):749-753.

ShangYongshuang,XuAiqiang,LiWenhai,etal.AnalysisofOptimalInspectionandMaintenancePolicywithPartiallyObservedInformation[J].SystemEngineeringandElectronics, 2012, 34(4):749-753.

[12]胡祥濤,張紅旗,李自成,等.基于部分可觀測Markov決策過程理論的盾構推進載荷規劃[J].機械工程學報,2014,50(21):84-91.

HuXiangtao,ZhangHongqi,LiZicheng，etal.POMDP-basedPlanningModelofDrivingForceDuringShieldTunneling[J].JournalofMechanicalEngineering, 2014, 50(21):84-91.

[13]MonahanGE.ASurveyofPartiallyObservableMarkovDecisionProcesses:Theory,Models,andAlgorithms[J].ManagementScience, 1982, 28(1):1-16.

[14]HuXiangtao,HuangYong’an,YinZhoupin,etal.DrivingForcePlanninginShieldTunnelingBasedonMarkovDecisionProcesses[J].Sci.ChinaTech.Sci., 2012, 55(4):1022-1030.

[15]PutermanML.MarkovDecisionProcesses:DiscreteStochasticDynamicProgramming[M].NewYork:JohnWiley&SonsInc，1994.

(編輯王艷麗)

Dynamic Reliability Assessment Method Based on POMDP for Electromechanical Equipment

Zhang Hongqi1,2Shao Xiaodong1Hu Xiangtao2

1.Xidian University, Xi’an，710071 2.CETC No.38 Research Institute,Hefei，230088

This paper focused on the operation and maintenance problems of electromechanical equipment, and proposed a new approach to assess the reliability and formulate the maintenance strategies based on POMDP theory. In the new approach, the dynamic reliability of electromechanical equipment was considered as an uncertain state which might be estimated by the monitoring informations (such as noise, pressure, temperature, vibration, et al.) according to POMDP theory. Furthermore, the influences of different maintenance strategies on reliability level of electromechanical equipment were investigated, and a dynamic reliability model was developed based on state transition. In order to plan the optimal maintenance strategy, an evaluation function was defined by minimizing the maintenance costs and the lost of faults. The experimental results confirm that the new approach based on POMDP is reasonable for electromechanical equipment, and possesses application and dissemination values.

reliability assessment; maintenance policy; partially observable Markov decision process(POMDP); electromechanical equipment

2015-05-04

國防技術基礎項目(JSZL2014210B001，JSBZ2014210A005，JSBZ2014210B007)；國防基礎科研項目(A1120131044)

TB114.3

10.3969/j.issn.1004-132X.2016.18.012

張紅旗，男，1975年生。中國電子科技集團公司第三十八研究所研究員、西安電子科技大學機電工程學院博士研究生。主要研究方向為數字化設計與制造、可靠性工程。發表論文20余篇。邵曉東，男，1970年生。西安電子科技大學機電工程學院教授、博士研究生導師。胡祥濤，男，1981年生。中國電子科技集團公司第三十八研究所高級工程師。