開煉機綠色塑煉參數建模及多目標優化

張　良　王其東　朱立紅　胡金芳

合肥工業大學，合肥，230009

?

開煉機綠色塑煉參數建模及多目標優化

張良王其東朱立紅胡金芳

合肥工業大學，合肥，230009

通過對開煉機塑煉過程的效率和能耗分析，構建了塑煉過程門尼黏度目標函數和碳排放目標函數。考慮塑煉過程中開煉機性能和塑煉參數的實際約束條件，建立以輥筒線速度、輥筒間距和輥筒速比為優化變量，以最小門尼黏度和最低碳排放為目標的多目標模型和量綱一單目標模型。應用改進遺傳算法對優化模型進行尋優求解。通過具體實例驗證了所建多目標優化模型的有效性和量綱一單目標模型的準確性，并對優化結果和優化變量的靈敏度進行了分析。

開煉機；塑煉參數；碳排放；多目標優化；遺傳算法

0　引言

塑煉是橡膠制品生產過程中的一個重要的加工過程[1]。在開煉機塑煉過程中，塑煉參數的合理選擇對提高橡膠企業的生產效率、降低生產成本、保障產品質量等有著重要的意義。以往，橡膠企業在實際生產過程中，一般只關注生產效率、生產成本和產品質量。隨著環境問題日益凸顯，越來越多的橡膠企業開始重視環境保護和節能減排工作。在橡膠制品加工過程中，廢氣排放主要來源于塑煉和硫化工序，這兩道工序的排放量占總排放量的90%[2]。因此，在保證產品質量、降低生產過程中碳排放的目標前提下，如何合理選擇生產設備和加工工藝參數成為眾多橡膠企業的一個迫切需要解決的實際工程問題。

目前，針對加工工藝參數優化決策問題，國內外有不少學者進行了研究。在機械加工方面，文獻[3-10]主要從最低能耗、最大材料去除率、最小生產成本、最優表面加工質量等方面進行研究，建立單一目標的優化模型；文獻[11-12]主要從成本、利潤、效率、能耗等方面建立多個目標函數，并運用遺傳算法、蟻群算法、粒子群算法等優化算法進行多目標優化。上述研究中，單目標優化已經不能滿足現代工藝優化的需求；多目標優化主要滿足高效、環保的需求，而忽略了產品的加工質量。在橡膠塑煉加工參數優化方面，相關的文獻報道較少，主要集中在國內。王冠中[13-14]運用神經網絡方法，建立了預測門尼黏度的橡膠開煉機塑煉工藝參數計算模型，并將計算結果與實驗結果進行對比,但他未對塑煉加工參數優化進行深入研究；謝清國[15]采用正交試驗法對橡膠加工質量進行了開煉機工藝參數優化，驗證了低溫一次法煉膠與傳統多段混煉方法相較在效率、煉膠質量等方面的優越性，但該研究僅對橡膠加工質量進行試驗優化，未進行理論分析和研究；曾憲奎等[16]、宋國宗[17]通過BP神經網絡建立橡膠塑煉工藝參數與塑煉質量指標之間的映射關系，運用遺傳算法進行目標優化，并通過正交試驗法驗證了遺傳算法最優工藝參數組合優于極差分析法最優工藝參數組合，但該研究僅考慮塑煉加工質量單一目標，未能涉及塑煉加工過程中的能耗和污染問題，不符合綠色加工的要求。

本文以加工質量和環境影響為綜合優化目標，對開煉機進行塑煉過程中工藝參數優化問題研究。建立了塑煉工藝參數數學模型，該模型以保障加工質量為前提，把碳排放最低作為優化目標，以開煉機設備和塑煉過程的實際情況為約束，運用遺傳算法對所建數學模型進行尋優求解，通過實例對該模型的有效性進行驗證。

1　塑煉參數優化模型的建立

1.1優化變量

在開煉機對橡膠材料進行低溫塑煉時，輥筒線速度(即前輥筒線速度)v2、輥距(前后兩輥筒之間的最小距離)e和輥筒速比(前后兩輥筒線速度之比)f是塑煉過程中重要的操作變量。這三個變量的值密切關系到開煉機的加工能力、加工效率和能量消耗。因此，將輥筒線速度v2、輥距e和輥筒速比f作為優化變量。

1.2優化目標函數

保證產品質量、提高生產效率是企業生存基礎；減少排放污染、滿足環境和社會的可持續發展是企業發展的前提，因此，需以保證塑煉過程中的橡膠性能為前提，優化塑煉過程的碳排放量[18]，以滿足綠色塑煉的工藝要求。

1.2.1塑煉過程門尼黏度目標函數

塑煉過程中，膠料的質量指標為門尼黏度、炭黑分散度、300%定伸應力、拉伸強度、撕裂強度等指標。其中，門尼黏度是尤其重要的質量指標[15,19]。在開煉機工作過程中，輥筒橫壓力的大小直接關系到膠料的門尼黏度[20]。如果將兩輥筒間隙內的膠料視為牛頓型流體，根據流體動力理論中的Navier-Stokes方程式，可以近似獲得膠料對輥筒的橫壓力：

(1)

式中，P為橫壓力;L為輥筒的工作長度;D為輥筒直徑;Kp為剪切系數，根據經驗，取Kp=200N/cm2。

根據文獻[21]提供的方法，膠料門尼黏度函數的數學模型可以近似地表示為

(2)

式中，U為門尼黏度;h1為供料厚度。

1.2.2塑煉過程碳排放函數

塑煉過程的碳排放主要包括加工過程消耗原材料引起的碳排放Cy、消耗電能引起的碳排放Cd、塑煉過程中產生邊角料的后期處理引起的碳排放Cb、塑煉過程產生廢氣和廢水的后期處理引起的碳排放Cq和Cw，如圖1所示(圖中“+”為碳排放量疊加)。

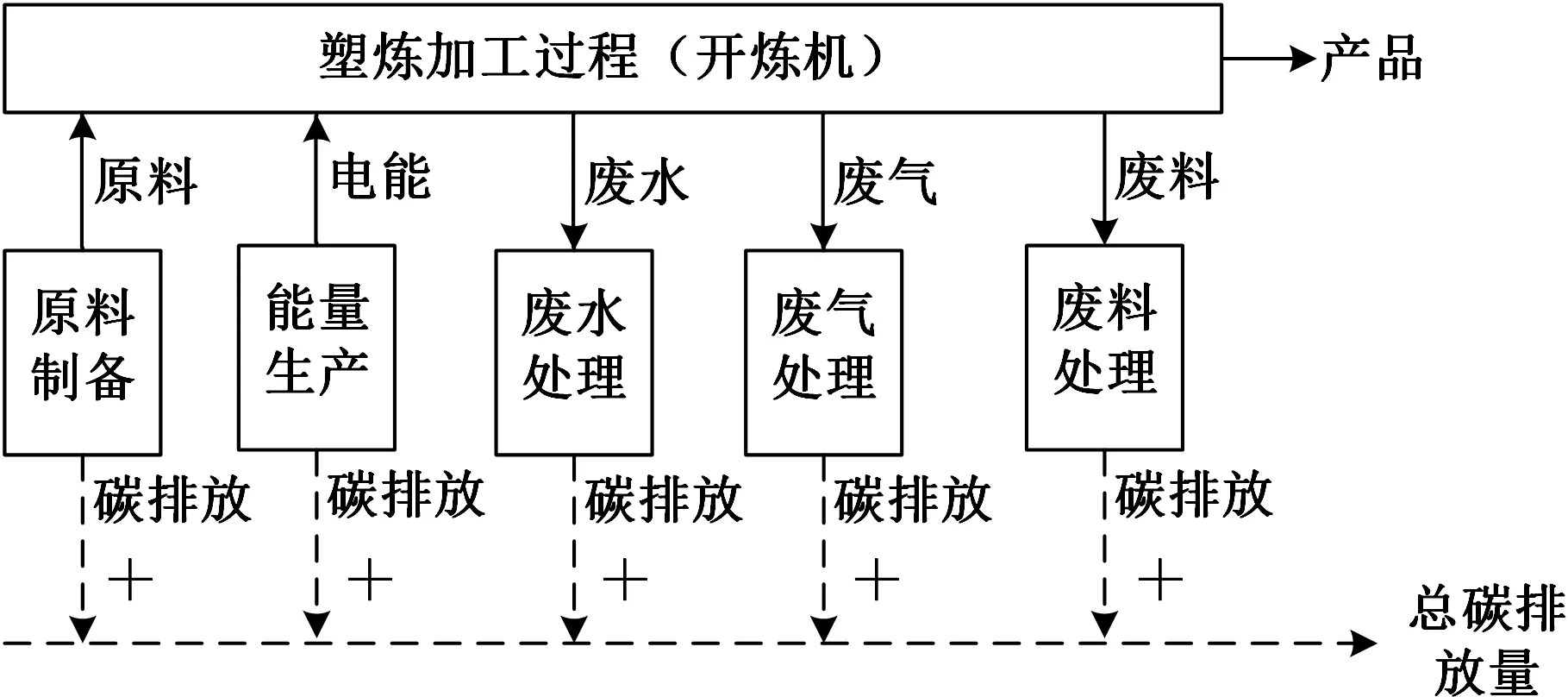
圖1　塑煉過程碳排放構成圖

塑煉過程對原材料消耗引起的碳排放Cy和廢料后處理碳排放Cb優化所作的貢獻非常有限，因此，對于塑煉過程參數優化問題，碳排放主要應考慮塑煉過程中電能消耗引起的碳排放Cd，廢氣處理引起的碳排放Cq，廢水處理引起的碳排放Cw，由此塑煉過程碳排放Ca可以表示為上述三部分碳排放之和，如下式所示:

Ca=Cd+Cq+Cw

(3)

1.2.2.1電能引起的碳排放Cd

在塑煉過程中，需要消耗大量電能。塑煉過程由電能消耗而引起的碳排放計算公式如下:

Cd=Fd,CO2Ed

(4)

式中，Fd,CO2為電能的碳排放因子，kg/(kW·h);Ed為塑煉過程電能消耗量。

(1)電能碳排放因子Fd,CO2的確定。電能碳排放因子與電網的構成有著密切的關系。表1是國家發展改革委員會應對氣候變化司2014年公布的中國幾大電網的排放因子[22]。本文采用幾大電網排放因子的平均值0.5412kg/(kW·h)作為電能碳排放因子。

表1　全國各區域電網碳排放因子

(2)塑煉時間T0的確定。根據文獻[23]的研究，在開煉機塑煉過程的時間T0內，開煉機的狀態主要可分為塑煉作業和空載兩種狀態。開煉機由空載狀態進入工作狀態時，會產生瞬時塑煉狀態，之后才進入穩定塑煉狀態。因此，塑煉作業狀態又可細分為瞬時塑煉狀態和穩定塑煉狀態。對應塑煉過程的三種狀態，塑煉時間可劃分為三個時間段，表示如下：

T0=Tk+Tw+Ts

(5)

式中，Tk為空載時間;Tw為穩定塑煉時間;Ts為瞬時塑煉時間。

由于塑煉時間受多種因素的影響，主要取決于物料性質、設備參數和工藝要求等，到目前尚無公認的時間計算方法。一般依據經驗，塑煉時間T0控制在20～40 min，穩定塑煉時間Tw約占總時間的70%，瞬時塑煉時間Ts約占塑煉時間T0的六分之一。

(3)塑煉過程電能消耗量Ed的確定。在塑煉時間T0內，開煉機總的輸入功率Pi分為三部分：空載功率Pk、瞬時塑煉功率Ps、穩定塑煉功率Pw。因此，在忽略一些微小波動的情況下，可近似地得到開煉機動態運行時能量平衡方程：

Ed=PiT0=PkTk+PwTw+PsTs

(6)

開煉機空載功率主要用于抵消動力傳遞過程中的嚙合功率損失、軸承摩擦功率損失和液力功率損失[24]。根據文獻[25-26]可近似得到開煉機空載功率Pk和瞬時塑煉功率Ps：

(7)

Ps=bsPw

(8)

式中，Pkd為開煉機最小空載功率；a1、a2為輥筒的轉速系數；bs為瞬時功率系數，根據經驗，bs=2。

由輥筒橫壓力可得膠料受到的剪切力：

Tj=Ptanρ

(9)

式中，ρ為摩擦角，5°≤ρ≤10°，本文計算中取ρ=7°。

由剪切力、剪切速度和穩定塑煉時間可得到穩定塑煉功率Pw：

Pw=(f2-1)v2DLKp(tanρ)Tw/(1.2×105e)

(10)

將式(6)、式(7)、式(8)和式(10)代入式(4)中，可得開煉機塑煉過程中電能引起的碳排放量：

Cd=Fd,CO2Ed=Fd,CO2PkTk+Fd,CO2PwTw+

Fd,CO2PsTs=Cdw+Cdk+Cds=

(f2-1)v2DLKp(tanρ)/(1.2×105e)

(11)

式中，Cdw、Cdk、Cds分別為穩定、空載和瞬時塑煉時的碳排放量。

1.2.2.2廢氣處理碳排放

橡膠材料在塑煉過程中，排放的廢氣污染物主要為粉塵顆粒物、CS2和非甲烷總烴[2]。一般采用集氣罩收集、物理吸附，然后借助風機將處理過的廢氣排入大氣。這一過程的碳排放主要來源于風機的能耗。故可得到廢氣處理碳排放表達式如下：

Cq=Fd,CO2PfjT0/60

(12)

式中，Pfj為風機的額定功率。

1.2.2.3廢水處理碳排放

橡膠制品企業中的廢水主要是用于冷卻的循環水，其水質污染物所占比重較少，其主要成分是水。參考文獻[27]中廢水處理碳排放因子的確定方法，獲得廢水處理的碳排放因子為0.2 kg/L。本文計算時采用該值。廢水處理碳排放計算采用在其循環周期內按時間標準折算到加工過程的分配方法，可簡化為一個塑煉工序時間的碳排放。具體計算方法如下：

Cw=0.2KDLT0/60

(13)

式中，K為捏煉容量經驗系數，一般取0.0065～0.0085。

將式(11)～式(13)代入式(3)，可得到塑煉工序中的碳排放函數為

Ca=Cd+Cq+Cw=

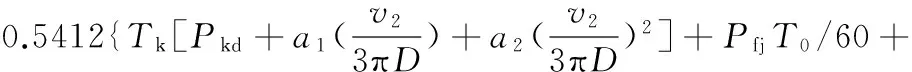
(14)

1.3約束條件

在開煉機的實際工作中，塑煉參數的取值要受到所選開煉機輥筒線速度范圍、速比范圍、輥距范圍等條件的限制，必須在滿足限制條件的范圍內取值。其中，輥筒線速度必須處于最小線速度v2min和最大線速度v2max之間；速比必須在開煉機允許的最小速比fmin和最大速比fmax之間；輥距必須在開煉機允許的最小輥距emin和最大輥距emax之間；開煉機瞬時功率應小于規定的最大有效塑煉功率Pmax。由此得到開煉機塑煉過程的多目標優化數學模型如下：

minF(v2,e,f)=(minU,minCa)

(15)

(16)

式中，η為開煉機有效功率系數。

2　基于遺傳算法的多目標優化

2.1多目標函數的優化表達

在進行多目標優化求解時，有時會得到多組解。為了獲得最優解，一般采用兩種方式，一種方式是從多組解中選出一組解作為最優解；另一種方式是將多目標的優化問題轉化為單目標問題進行求解。本文采用加權求和法將多目標優化問題轉化為單目標優化問題進行求解。轉化后的單目標函數為

minF(v2,e,f)=min (r1U+r2Ca)

式中，r1、r2為權系數，并且r1+r2=1，可以采用模糊評價法、層次分析法、粗集理論等方法得到。

對門尼黏度目標函數和碳排放目標函數進行量綱一化處理，具體方法如下：

式中，Umin、Umax分別為單目標門尼黏度函數優化的最小值和最大值；Cmin、Cmax分別為單目標碳排放函數優化的最小值和最大值。

量綱一化后的單目標優化函數為

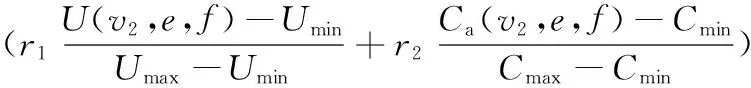
(17)

2.2遺傳算法優化過程

將Pareto的概念與遺傳算法相結合[28]，在遺傳算法的基礎上，增加了群體排序、小生境、適應值共享機制等技術，對開煉機塑煉參數進行多目標優化，其算法程序如圖2所示，其中選取最大代數G=100，種群的規模為100，采用十進制編碼，雜交概率為0.7，變異概率為0.05。

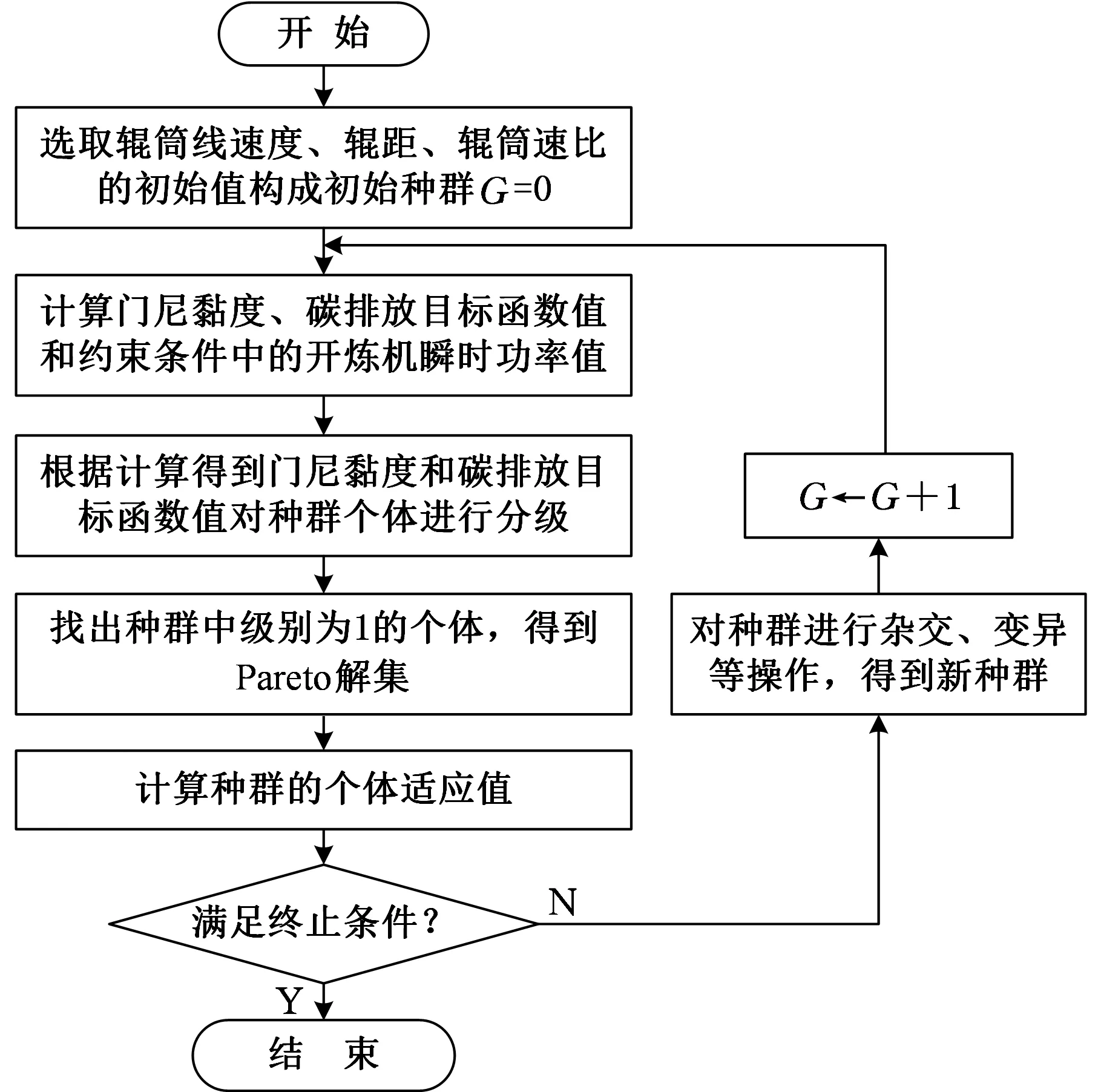
圖2　優化算法流程圖

3　優化實例驗證

以在某型號開煉機上塑煉某品牌661型空氣彈簧膠料為例驗證前文所建優化模型的有效性。

3.1實驗條件

實驗所用開煉機基本參數如表2所示。

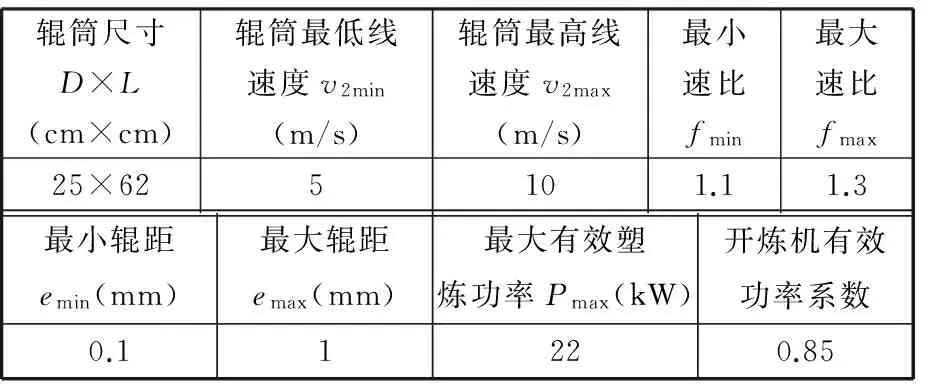
表2　開煉機規格參數

實驗用661型空氣彈簧，質量為12 kg。其他計算相關參數和系數見表3～表5。表中數據來源于橡膠加工企業。

表3　計算相關參數和系數

表4　塑煉參數初始值

表5　塑煉時間參數　min

3.2優化結果及分析

利用MATLAB工具箱編寫程序進行優化計算。利用層次分析法可得式(17)中的權重值，r1=r2=0.5。本實例對量綱一化處理后的單目標優化結果如表6所示。

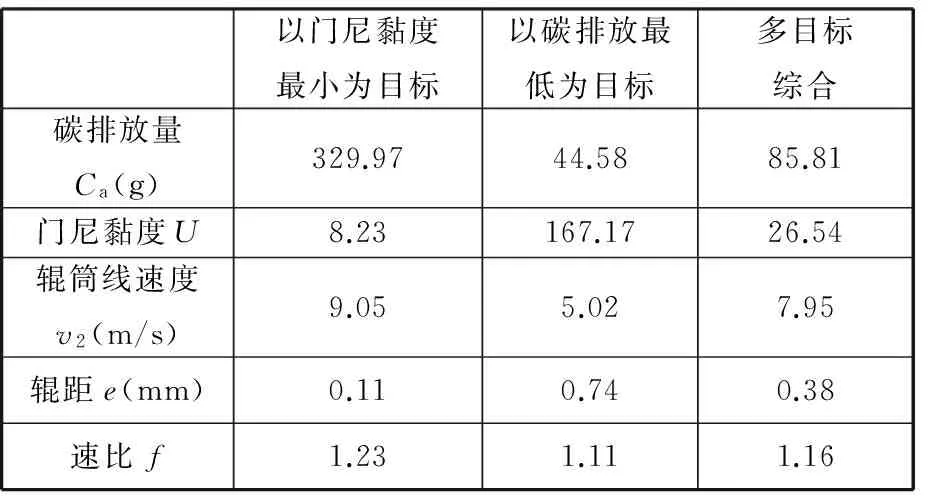
表6　單目標函數優化結果

分析表6和圖3可知，和單一目標優化相比，對門尼黏度和碳排放量進行多目標綜合優化效果較為明顯；以門尼黏度最小為目標時，輥筒線速度最快，速比最大，輥距最小，開煉機的穩定塑煉功率和瞬時塑煉功率均較大，碳排放量也相對較大，但其門尼黏度最低；以碳排放最低為目標時，輥筒線速度最低，速比最小，輥距較大，導致開煉機的穩定塑煉功率和瞬時塑煉功率均最小，使得開煉機耗能引起的碳排放量最小，但門尼黏度較大；而多目標綜合優化時，塑煉過程的門尼黏度值和碳排放量介于兩者之間，是在保證較低的門尼黏度的情況下，碳排放量最少，因此綜合目標最優。

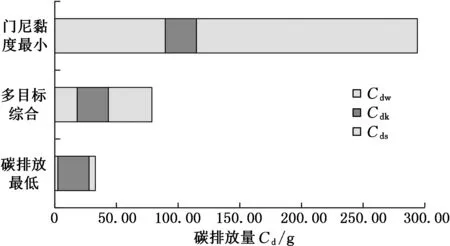
圖3　不同塑煉參數下的電能引起的碳排放量構成

本實例對式(15)和式(16)直接進行多目標優化獲得三組解，結果如表7所示。

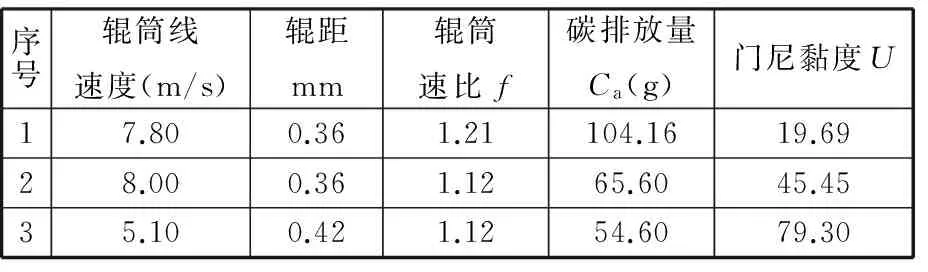
表7　多目標函數優化結果

將表7中的三組解兩兩進行加權求和，權重值取r1=r2=0.5，結果見表8。

將表8中的三組解與表6中綜合優化目標的結果進行比較可知，加權后的三組解中只有第一組解與單目標函數綜合優化結果相近，碳排放相近度達99%，而門尼黏度值卻有22.7%的差距。可見，本例中使用量綱一化后的單目標優化效果較好。

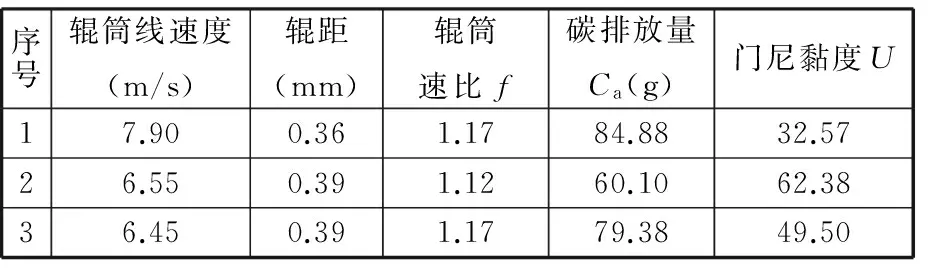
表8　加權后的結果

3.3靈敏度分析

為了分析三個優化變量在優化區間內取不同值時對目標函數的影響程度，將各優化變量的大小增加10%，比較目標函數的變化程度，結果如圖4～圖6所示。根據正交試驗法的原則，分別從圖4～圖6中選取部分參數值來定量分析靈敏度，結果如表9所示。

圖4　目標函數值隨輥距變化

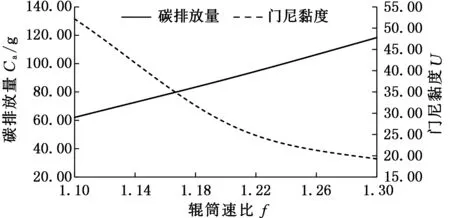
圖5　目標函數值隨速比變化

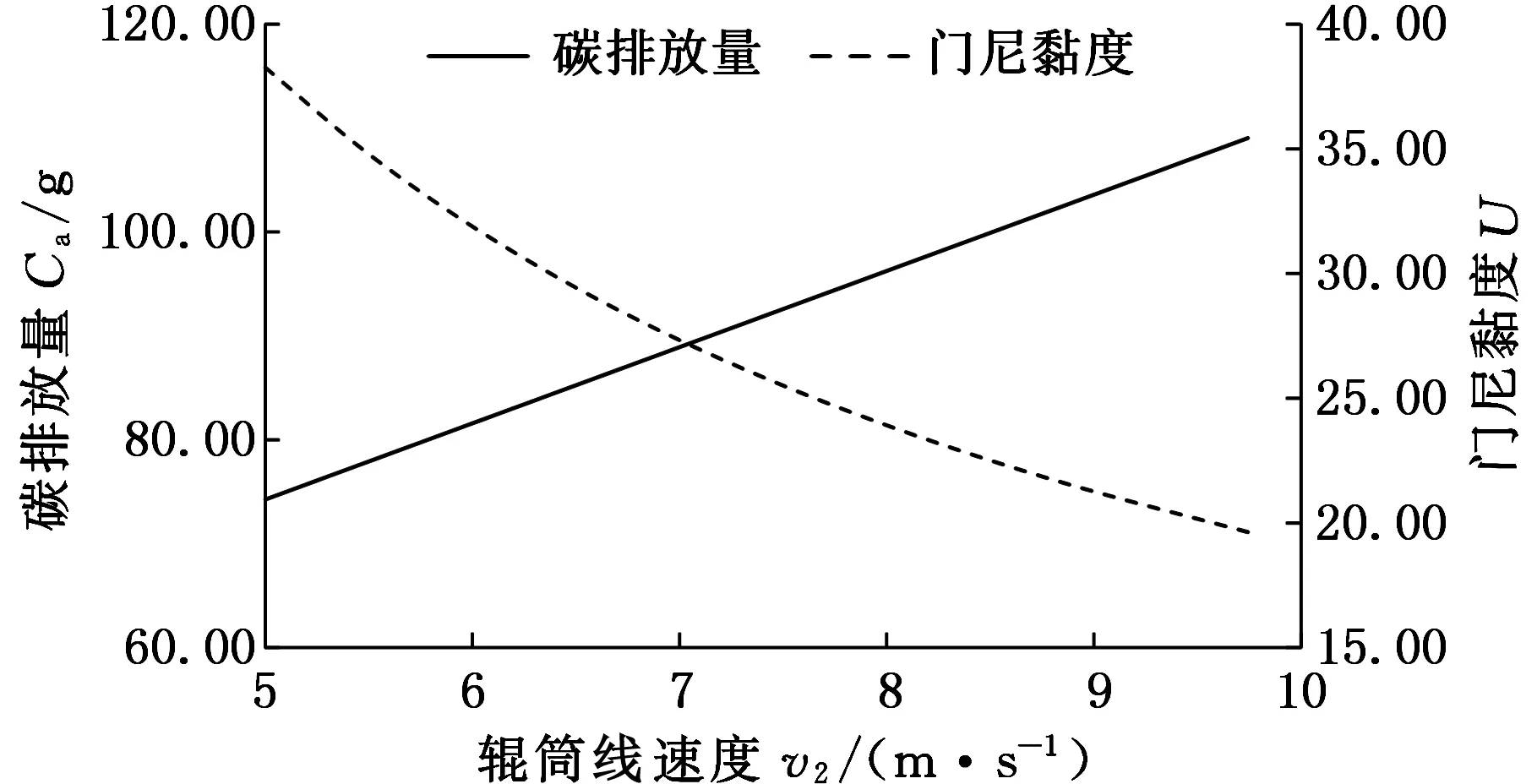
圖6　目標函數值隨輥筒線速度變化

圖4～圖6表示了各個優化變量值在優化區間內單調遞增時，碳排放量和門尼黏度變化趨勢。由圖4可以看出，隨著輥距的增大，兩輥輪間的剪切力減小，門尼黏度呈現逐漸增大趨勢。同時，開煉機功率減小，碳排放量也隨之減小；分析圖5可知，隨著輥筒速比增加，兩輥輪間的剪切力增大，門尼黏度隨之減小。同時可知，開煉機功率增大，碳排放量呈現逐漸增大趨勢；由圖6可以看出，隨著輥筒線速度的增大，門尼黏度呈現減小趨勢，碳排放量呈現單調增加趨勢。

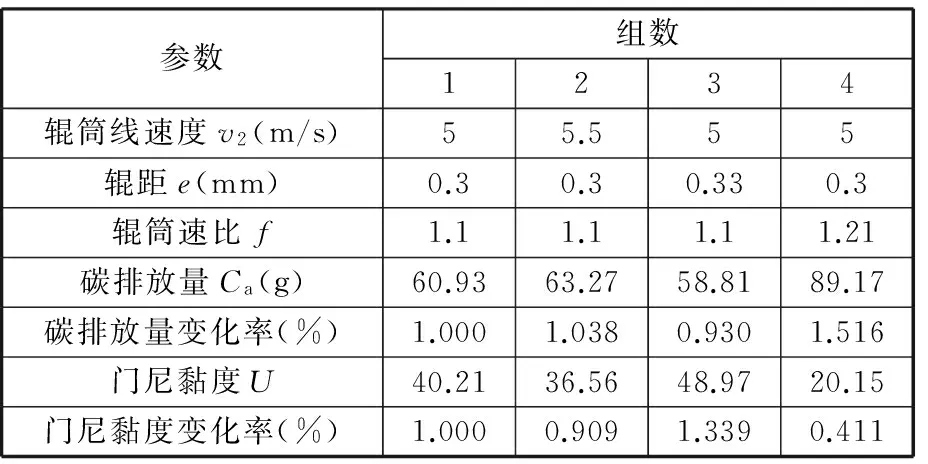
表9　靈敏度分析選用的部分變量數值

分析表9可知，當速比增大10%時，碳排量增大51.6%，門尼黏度減小58.9%；當輥距增大10%時，碳排量減小7%，門尼黏度增大33.9%；當輥筒線速度增大10%時，碳排放量增大3.8%，門尼黏度減小8.9%。

由圖4～圖6和表9的分析可知，速比對碳排放量和門尼黏度的影響最大，輥距對門尼黏度的影響也較大，輥筒線速度對碳排放量和門尼黏度的影響均較小。因此，在以門尼黏度和碳排放量為目標時應選擇速比的中間值、較小的輥距和輥筒線速度。

4　結語

本文建立了一種基于加工質量的綠色塑煉參數優化模型。在分析開煉機低溫塑煉過程的基礎上，選取輥筒線速度、輥距和輥筒速比為優化變量，以門尼黏度和塑煉過程碳排放為優化目標，門尼黏度用來對膠料加工質量進行評價，碳排放量表明了對塑煉過程綠色化的訴求。結合塑煉過程開煉機功率的約束，引入各優化變量合理取值范圍，利用Pareto遺傳算法對模型進行尋優求解，通過具體實例，對多目標優化結果和量綱一化后的單目標優化結果進行對比，驗證了模型的有效性。通過定量計算，進一步分析了不同優化變量對目標函數的靈敏度，為橡膠加工企業保質、低碳環保訴求提供了一種有效的理論計算方法。研究結果表明，本方法對保證加工質量、降低碳排放有一定的工程應用價值。

本方法僅針對低溫塑煉工藝的參數優化，下一步將重點研究包含塑煉時間和溫度的多目標優化方法。

[1]呂百齡.實用橡膠手冊[M].北京：化學工業出版社,2010.

[2]丁學鋒,張慧君,曹睿.橡膠制品工業工藝廢氣排放因子探討——以輪胎企業為例[J].四川環境,2013,32(6):83-86.

DingXuefeng,ZhangHuijun,CaoRui.DiscussiononWasteGasEmissionFactorsofRubberProductsIndustryProcess—aCaseStudyofTireEnterprises[J].SichuanEnvironment,2013,32(6):83-86.

[3]TandonV,EI-MounayriH,KishawyH.NCEndMillingOptimizationUsingEvolutionaryComputation[J].InternationalJournalofMachineTool&Manufacture,2002,42(5):595-605.

[4]SaravananR,AsokanP,VijayakumanK.MachiningParametersOptimizationforTurningCylindricalStockintoaContinuousFinishedProfileUsingGeneticAlgorithm(GA)andSimulatedAnnealing(SA)[J].InternationalJournalofAdvancedManufacturingTechnology,2003,21(1):1-9.

[5]RajemiMF,MativengaPT,AramcharoenA.SustainableMachining:SelectionofOptimumTurningConditionsBasedonMinimumEnergyConsiderations[J].JournalofCleanerProduction,2010 (18):1059-1065.

[6]AzlanMZ,HabibollahHSS.ApplicationofGAtoOptimizeCuttingConditionsforMinimizingSurfaceRoughnessinEndMillingMachiningProcess[J].ExpertSystemwithApplications,2010,37:4650-4659.

[7]WuMP,LiaoWH.Internet-basedMachiningParameterOptimizationandManagementSystemforHigh-speedMachining[J].TransactionsofNanjingUniversityofAeronauticsandAstronautics,2005,22(1):42-46.

[8]MoriM,FujishimaM,InamasuY,etal.AStudyonEnergyEfficiencyImprovementforMachineTools[J].ManufacturingTechnology,2011,60(1):145-148.

[9]謝書童,郭隱彪.數控車削中成本最低的切削參數優化方法[J].計算機集成制造系統,2011,10(17):2144-2149.

XieShutong,GuoYinbiao.OptimizationApproachofCuttingParametersforMinimizingProductionCostinCNCTurnings[J].ComputerIntergratedManufacturingSystems,2011,10(17):2144-2149.

[10]陳志同,張保國.面向單元切削過程的切削參數優化模型[J].機械工程學報,2009,45(5):230-243.

ChenZhitong,ZhangBaoguo.MathematicModelonCuttingParameterOptimizationforUnitCuttingProcess[J].JournalofMechanicalEngineering,2009,45(5):230-243.

[11]李聰波,崔龍國,劉飛,等.面向高效低碳的數控加工參數多目標優化模型[J].機械工程學報,2013,49(9):87-96.

LiCongbo,CuiLongguo,LiuFei,etal.MultiobjectiveNCMachingParametersOptimizationModelforHighEfficientandLowCarbon[J].JournalofMechanicalEngineering,2013,49(9):87-96.

[12]李堯,劉強.面向服務的綠色高效銑削優化方法研究[J].機械工程學報,2015,51(11):89-98.

LiYao,LiuQiang.Service-orientedResearchonMulti-passMillingParametersOptimizationforGreenandHighEfficiency[J].JournalofMechanicalEngineering,2015,51(11):89-98.

[13]WangGuanzhong.ResearchMethodoftheRubber’sPlasticizationTechnologicalParameterOptimizeonOpenMillbyNeuralNetwork[J].AdvancedMaterialsResearch,2010,87/88:509-512.

[14]王冠中.橡膠開煉機塑煉工藝優化的神經網絡研究方法[J].特種橡膠制品,2011,31(6):55-57.

WangGuanzhong.OptimizationofRubberPlasticizationTechnologicalParametersonOpenMillbyNeuralNetwork[J].SpecialPurposeRubberProducts,2011,31(6):55-57.

[15]謝清國.低溫一次法混煉機理及實驗研究[D].青島:青島科技大學,2011.

[16]曾憲奎,張宗廷,呂沖.開煉機煉膠工藝參數2種優化方法的對比研究[J].特種橡膠制品, 2015(1):67-70.ZengXiankui,ZhangZongting,LüChong.ComparativeStudyofOpenMillMixingProcessParametersofTwoKindsofOptimizationMethods[J].SpecialPurposeRubberProducts,2015(1):67-70.

[17]宋國宗.開煉機煉膠工藝參數多目標優化研究[D].青島：青島科技大學,2014.

[18]羅毅,曹華軍,李洪丞,等.基于GRNN網絡的CO2氣體保護焊工藝碳排放建模與參數優化[J].中國機械工程,2013,24(17):2398-2403.

LuoYi,CaoHuajun,LiHongcheng,etal.CarbonEmissionModelandParameterOptimizationofCO2ShieldedWeldingBasedonGRNN[J].ChinaMechanicalEngineering,2013,24(17):2398-2403.

[19]曾憲奎,劉威,張宗廷,等.用統計分析軟件SPSS建立橡膠開煉機門尼黏度在線預測數學模型[J].合成橡膠工業,2015,38(5):358-362.

ZengXiankui,LiuWei,ZhangZongting,etal.EstablishmentofOnlinePredictionMathematicalModelforMooneyViscosityofRubberOpenMillUsingStatisticalAnalysisSoftwareSPSS[J].ChinaSyntheticRubberIndustry,2015,38(5):358-362.

[20]曹偉魏.開煉機輥筒的有限元分析及其優化設計[D].長沙：中南林業科技大學,2013.

[21]任娜.基于神經網絡的橡膠開煉機煉膠質量在線預測技術的研究[D].青島：青島科技大學,2014.

[22]國家發展改革委應對氣候變化司.2014年中國區域電網基準線排放因子[EB/OL].(2015-02-05)[2015-11-18].http://www.tangongye.com/CarbonAsset/NewShow.aspx?id=7502.

[23]梁基照.開煉機煉膠過程中能量的平衡與計算[J].化工裝備技術,1988(1):10-14.

LiangJizhao.TheEnergyBalanceandCalculationofOpenMillMixingProcess[J].ChemicalEquipmentTechnology,1988(1):10-14.

[24]曹勁然,馮毅,陸寶春,等.基于組合核函數OSVR算法的起重機減速齒輪箱磨損趨勢預測[J].中國機械工程,2015,26(5):641-646.

CaoJinrang,FengYi,LuBaochun,etal.WearTrendPredictionofCraneGearboxBasedonOSVRMethodwithCombinedKernelFunctions[J].ChinaMechanicalEngineering,2015,26(5):641-646.

[25]巫靜安,李木松.橡膠加工機械[M].北京:化學工業出版社，2006.

[26]施金良,劉飛,許弟建,等.數控機床空載運行時節能決策模型及實用方法[J].中國機械工程,2009,20(11):1344-1346.

ShiJinliang,LiuFei,XuDijian,etal.DecisionModelandPracticalMethodofEnergySavinginNCMachineTool[J].ChinaMechanicalEngineering,2009,20(11):1344-1346.

[27]國家標準化委員會.GB27632-2011橡膠制品工業污染物排放標準[S].北京:中國環境科學出版社,2012.

[28]王海艷,秦旭達,任成祖.基于Pareto遺傳算法的螺旋銑加工參數優化[J].中國機械工程,2012,23(17):2058-2061.

WangHaiyan,QinXuda,RenChengzu.OptimizationofCuttingParametersinHelicalMillingProcessBasedonParetoGeneticAlgorithm[J].ChinaMechanicalEngineering,2012,23(17):2058-2061.

(編輯王艷麗)

Green Mastication Parameter Modeling of Open Mill and Multi-objective Optimization

Zhang LiangWang QidongZhu LihongHu Jinfang

Hefei University of Technology,Hefei,230009

Through the analyses of the efficiency and energy consumption of the mastication processes of an open mill, the Mooney viscosity objective function and carbon emissions objective function were established. Considering the actual constraints in the processes of open mill performance and mastication parameters, a multi-objective optimization model and a dimensionless single objective model were established, which took the open mill linear speed of roller, roller spacing and roller ratio as the variables, the minimum Mooney viscosity and the lowest carbon emission as the optimization objectives. An improved genetic algorithm was used to solve the optimization model. An experimental case was performed to verify the effectiveness and accuracy of the optimization model, and the mastication parameter optimization results and the sensitivity of optimization variables were analyzed.

open mill; mastication parameter; carbon emissions; multi-objective optimization; genetic algorithm

2015-11-18

國家自然科學基金資助項目(51175135)

TH17

10.3969/j.issn.1004-132X.2016.18.015

張良，男，1973年生。合肥工業大學機械與汽車工程學院講師、博士研究生。主要研究方向為現代汽車設計理論及控制技術。發表論文10余篇。王其東，男，1964年生。合肥工業大學機械與汽車工程學院教授、博士研究生導師。朱立紅(通信作者)，女，1974年生。合肥工業大學機械與汽車工程學院講師、博士。胡金芳，女，1983年生。合肥工業大學機械與汽車工程學院講師、博士。