面向能耗的數(shù)控銑削過程建模與參數(shù)優(yōu)化
黃拯滔 楊 杰 張超勇 周志恒 謝 陽 林文文
1.華中科技大學(xué)數(shù)字制造裝備與技術(shù)國家重點(diǎn)實(shí)驗(yàn)室,武漢,4300742.中國地質(zhì)大學(xué)(武漢),武漢,430074
?
面向能耗的數(shù)控銑削過程建模與參數(shù)優(yōu)化
黃拯滔1楊杰2張超勇1周志恒1謝陽1林文文1
1.華中科技大學(xué)數(shù)字制造裝備與技術(shù)國家重點(diǎn)實(shí)驗(yàn)室,武漢,4300742.中國地質(zhì)大學(xué)(武漢),武漢,430074
為了選擇合理的切削參數(shù)以達(dá)到降低能耗的目的,對(duì)穩(wěn)定的數(shù)控銑削過程面向能耗進(jìn)行建模并優(yōu)化。首先,在分析輸入功率去向構(gòu)成的基礎(chǔ)上,建立數(shù)控銑床系統(tǒng)輸入功率模型。然后,建立數(shù)控銑床系統(tǒng)能耗測(cè)試平臺(tái)。通過對(duì)實(shí)驗(yàn)數(shù)據(jù)的多元回歸建立數(shù)控銑床輸入功率與切削參數(shù)的函數(shù),對(duì)比分析證實(shí)函數(shù)的精確性。隨后,由該函數(shù)得出數(shù)控銑床穩(wěn)定切削階段的單位體積能耗函數(shù),以此為優(yōu)化目標(biāo),以銑床性能和表面質(zhì)量為約束,通過引力搜索算法(GSA)進(jìn)行切削參數(shù)的能效優(yōu)化。最后,與經(jīng)驗(yàn)的切削參數(shù)進(jìn)行對(duì)比,結(jié)果表明優(yōu)化后切削參數(shù)顯著提高了銑床能量效率,大幅節(jié)省了電能。
數(shù)控銑床;節(jié)能;功率模型;切削參數(shù)優(yōu)化;引力搜索算法
0 引言
數(shù)控機(jī)床系統(tǒng)能耗建模一直以來都是學(xué)術(shù)界研究的熱點(diǎn),近年來一系列數(shù)控機(jī)床系統(tǒng)能耗的間接建模方法逐漸發(fā)展起來。Abele等[1]提出基于理論公式的生命周期評(píng)估(LCA)方法,來估算產(chǎn)品制造過程的能耗。但是Steiner等[2]認(rèn)為,LCA方法只能得到一定時(shí)間段內(nèi)的能耗平均值,而且其精度在很大程度上依賴于模型設(shè)定參數(shù)的完備性。Jiang等[3]提出一種基于BP神經(jīng)網(wǎng)絡(luò)的機(jī)床加工過程能耗評(píng)估模型,但該方法需要大量的切削實(shí)驗(yàn)來使神經(jīng)細(xì)胞積累經(jīng)驗(yàn),獲得評(píng)估模型。Aggarwal等[4]采用實(shí)驗(yàn)方法來預(yù)測(cè)機(jī)床系統(tǒng)能耗,他們分別采用了響應(yīng)面法(RSM)和田口方法(Taguchi method)來分析各個(gè)切削參數(shù)對(duì)輸入功率的影響程度,進(jìn)而得出數(shù)控機(jī)床系統(tǒng)的輸入功率模型。但是該方法所得模型能量構(gòu)成成分不明,物理意義不明確,建立模型需要大量實(shí)驗(yàn)。
為了更加清晰地了解數(shù)控機(jī)床系統(tǒng)輸入功率的構(gòu)成,各耗能部件的功率比重,學(xué)者們?cè)絹碓街匾晱哪芰苛飨虻慕嵌葋碇苯咏!utowski 等[5]首先提出了利用能量守恒定律,通過機(jī)床系統(tǒng)能量流向來估算工藝過程的能耗。他們將機(jī)床系統(tǒng)功率分為不變部分和可變部分,以材料去除率vMRR作為變量,建立輸入功率Pi與vMRR之間的函數(shù)關(guān)系。但是,該模型忽略了主軸轉(zhuǎn)動(dòng)和進(jìn)給運(yùn)動(dòng)在機(jī)床傳動(dòng)鏈中造成的機(jī)械損耗。Li 等[6]針對(duì)這個(gè)問題進(jìn)行深入探索,將機(jī)床系統(tǒng)的機(jī)械損耗納入考慮,增加了主軸轉(zhuǎn)速n作為變量,進(jìn)一步完善了機(jī)床系統(tǒng)輸入功率模型,使得對(duì)機(jī)床系統(tǒng)加工過程的能耗估算更加精確。劉飛等[7]從多源能量流的角度出發(fā),建立了理論基礎(chǔ)十分完善的機(jī)電主傳動(dòng)系統(tǒng)能量模型,該模型理論健全,表達(dá)清晰,具有相當(dāng)?shù)挠?jì)算精度,但是所包含的電信號(hào)變量、運(yùn)動(dòng)信號(hào)變量較多,信號(hào)采集復(fù)雜,對(duì)于現(xiàn)場(chǎng)實(shí)施有相當(dāng)大的難度。
數(shù)控機(jī)床系統(tǒng)建模的目的是深入解析其運(yùn)行機(jī)制,從而優(yōu)化其參數(shù)設(shè)置以達(dá)到高效利用資源和設(shè)備、提高產(chǎn)品質(zhì)量的目的。目前機(jī)床切削參數(shù)的優(yōu)化主要集中在對(duì)加工效率、表面質(zhì)量、刀具壽命和生產(chǎn)成本的改善上。Sonmez等[8]采用幾何規(guī)劃的方法對(duì)多工步銑削加工的工序時(shí)間進(jìn)行優(yōu)化,而Wang等[9]則采用了混合的遺傳算法與模擬退火算法來優(yōu)化這一目標(biāo)。Tandon等[10]采用神經(jīng)網(wǎng)絡(luò)預(yù)測(cè)端銑切削力并運(yùn)用粒子群算法優(yōu)化生產(chǎn)成本。劉海江等[11]采用線性加權(quán)的方法對(duì)數(shù)控車床的生產(chǎn)率和生產(chǎn)成本進(jìn)行綜合優(yōu)化。Jafarian等[12]運(yùn)用神經(jīng)網(wǎng)絡(luò)、遺傳算法和粒子群算法對(duì)車削過程的表面質(zhì)量、刀具壽命和切削力進(jìn)行了建模和綜合優(yōu)化。近年來數(shù)控加工系統(tǒng)能耗的關(guān)注度逐漸提高,但能耗的優(yōu)化則主要關(guān)注于加工的排程、工序間的空載時(shí)間與工序內(nèi)空載調(diào)速方式的優(yōu)化。He等[13]對(duì)柔性制造系統(tǒng)采用事件圖方法進(jìn)行面向任務(wù)的能耗建模,并優(yōu)化加工任務(wù)的排程方案以節(jié)省待機(jī)時(shí)間,提高車間能效。文獻(xiàn)[14]通過動(dòng)態(tài)調(diào)節(jié)工序內(nèi)機(jī)床空載運(yùn)行轉(zhuǎn)速實(shí)現(xiàn)按照最節(jié)能的方式調(diào)速。文獻(xiàn)[15]則通過建立機(jī)床工步間空載運(yùn)行啟停機(jī)節(jié)能決策模型來改善機(jī)床能效。數(shù)控機(jī)床系統(tǒng)節(jié)能更多在加工輔助階段實(shí)施,對(duì)切削過程的能量效率的提升仍有所缺失。
由于數(shù)控機(jī)床系統(tǒng)多源能量流模型復(fù)雜,且機(jī)床的切削功率、機(jī)械損耗等難以直接測(cè)量,使得要建立輸入功率Pi與切削參數(shù)之間的對(duì)應(yīng)關(guān)系十分困難。本文以數(shù)控銑床系統(tǒng)為例,從Gutowski 等[5]所提出的模型出發(fā),充分考慮數(shù)控銑床系統(tǒng)的機(jī)械損耗和負(fù)載損耗,力圖全面考慮數(shù)控銑床系統(tǒng)輸入功率的流向,用較簡單的監(jiān)測(cè)設(shè)備和測(cè)試數(shù)據(jù),采用分項(xiàng)擬合的方式建立更加完善的輸入功率模型,找到Pi與切削參數(shù)之間更加精確的函數(shù)關(guān)系。在提出模型的基礎(chǔ)上,以穩(wěn)定切削過程最小單位體積能耗ESEC為目標(biāo),考慮數(shù)控銑床系統(tǒng)加工能力和加工表面質(zhì)量要求等約束條件,采用新型的引力搜索算法對(duì)切削參數(shù)進(jìn)行優(yōu)化,達(dá)到提高機(jī)床系統(tǒng)加工過程能量效率、節(jié)約能源的目標(biāo)。
1 問題建模
1.1功率模型
數(shù)控機(jī)床系統(tǒng)穩(wěn)定切削階段的輸入功率Pi可分為兩個(gè)部分:固定功率P0和可變功率Pvar。固定功率P0即數(shù)控機(jī)床系統(tǒng)輸入功率中與工作狀態(tài)無關(guān)的那一部分功率,主要被照明燈、控制系統(tǒng)、風(fēng)扇、液壓泵、空氣壓縮機(jī)等消耗。它們?cè)跀?shù)控機(jī)床系統(tǒng)總電源開啟之時(shí)即啟動(dòng),工作狀態(tài)恒定,功率不隨機(jī)床工作狀態(tài)的變化而改變。
數(shù)控機(jī)床系統(tǒng)的可變功率也可劃分為兩個(gè)部分:空載相關(guān)功率Pidle和負(fù)載相關(guān)功率Pload,具體見圖1。現(xiàn)代數(shù)控機(jī)床主要采用“變頻器+異步電機(jī)+機(jī)械傳動(dòng)”的主軸驅(qū)動(dòng)方式和“伺服驅(qū)動(dòng)器+伺服電機(jī)+機(jī)械傳動(dòng)”的進(jìn)給驅(qū)動(dòng)方式[16]。其中變頻器(伺服驅(qū)動(dòng)器)的功率損耗ΔP是與變頻頻率f與變頻器回路阻抗Zf相關(guān)的復(fù)雜函數(shù),電動(dòng)機(jī)電磁損耗功率Ple則與電動(dòng)機(jī)回路阻抗Zd密切相關(guān),有
ΔP=f(finv,Zf)
(1)
Ple=f(Zd)
(2)

圖1 數(shù)控機(jī)床系統(tǒng)輸入功率構(gòu)成
變頻器阻抗Zf和電動(dòng)機(jī)阻抗Zd均與負(fù)載密切相關(guān),但對(duì)應(yīng)的精確的函數(shù)關(guān)系至今尚未建立。由于空載狀態(tài)下,數(shù)控機(jī)床系統(tǒng)的變頻器(伺服驅(qū)動(dòng)器)功率損耗ΔP和電動(dòng)機(jī)電磁損耗功率Ple數(shù)值不大,相對(duì)于數(shù)控機(jī)床系統(tǒng)的輸入功率的比例較小,因此在建模過程中忽略不計(jì)。
數(shù)控機(jī)床系統(tǒng)的機(jī)械傳動(dòng)損耗在主軸傳動(dòng)系統(tǒng)和進(jìn)給傳動(dòng)系統(tǒng)之中均有發(fā)生,即機(jī)械傳動(dòng)損耗功率Pmec包括主軸系統(tǒng)機(jī)械損耗功率和進(jìn)給系統(tǒng)機(jī)械損耗功率,這兩個(gè)損耗功率又分別由兩類損耗組成:與角速度成正比的庫侖摩擦損耗和與角速度的平方成正比的黏性摩擦損耗[7],即
Pmec=Pspindle+Pfeed
(3)
(4)
(5)
式中,Pspindle、Pfeed分別為主軸系統(tǒng)和進(jìn)給系統(tǒng)機(jī)械損耗;M1、M2分別為相應(yīng)的等效庫侖摩擦力矩;B1、B2分別為相應(yīng)的等效阻尼系數(shù);a1、b1分別為主軸系統(tǒng)一階、二階機(jī)械損耗系數(shù);a2、b2分別為進(jìn)給系統(tǒng)相應(yīng)的損耗系數(shù);ω1、ω2分別為主軸電機(jī)和進(jìn)給電機(jī)的等效角速度;n為主軸轉(zhuǎn)速;f為進(jìn)給速率。
實(shí)驗(yàn)發(fā)現(xiàn),進(jìn)給機(jī)械損耗功率Pfeed較小,不到主軸機(jī)械損耗功率Pspindle的十分之一。在不失準(zhǔn)確性的前提下,為降低模型復(fù)雜度,進(jìn)給系統(tǒng)的黏性摩擦損耗忽略不計(jì)。因此進(jìn)給機(jī)械損耗功率Pfeed可簡化為
Pfeed=a2f
(6)
負(fù)載相關(guān)功率Pload是指數(shù)控機(jī)床系統(tǒng)在進(jìn)入切削狀態(tài)之后,由切削載荷帶來的功率消耗。負(fù)載相關(guān)功率由兩個(gè)部分組成:切削功率Pcutting和載荷損耗功率Ploss。切削功率Pcutting作為數(shù)控機(jī)床系統(tǒng)的有效輸出,長期以來一直都是學(xué)術(shù)界研究的熱點(diǎn)。理論上可以通過主軸電流對(duì)切削功率進(jìn)行相對(duì)準(zhǔn)確的評(píng)估,但是該方法尚有兩個(gè)顯著的缺陷:一方面主軸電流只能對(duì)切削功率進(jìn)行實(shí)時(shí)的監(jiān)控,不能對(duì)不同切削條件下的切削功率作出提前預(yù)估;另一方面主軸電流作為一個(gè)被動(dòng)變量不能成為數(shù)控機(jī)床系統(tǒng)能量優(yōu)化的對(duì)象,該方法不能用以提高機(jī)床能量效率。切削力Fc的指數(shù)型經(jīng)驗(yàn)公式很好地克服了上述缺陷,并且對(duì)切削力的預(yù)測(cè)較為精確,非常適用于評(píng)估切削功率Pcutting。切削力Fc的指數(shù)型經(jīng)驗(yàn)公式如下:
(7)
(8)
式中,vc為切削速度;fz為每齒進(jìn)給量;ap為切削深度;ae為切削寬度;x、y、w、u分別為相應(yīng)的影響系數(shù);k為切削力矯正系數(shù)。
載荷損耗功率Ploss是指由數(shù)控機(jī)床系統(tǒng)切削載荷引起的除切削功率Pcutting以外其他損耗功率的總稱。它包含發(fā)生在變頻器(伺服驅(qū)動(dòng)器)、電動(dòng)機(jī)以及機(jī)械傳動(dòng)環(huán)節(jié)由載荷引起的功率損耗。該部分損耗功率產(chǎn)生的機(jī)理復(fù)雜,難以用切削參數(shù)直接表達(dá)。實(shí)驗(yàn)證實(shí),載荷損耗功率Ploss與切削功率Pcutting近似成正比[7],即
Ploss=αPcutting
(9)
Pload=Pcutting+Ploss
(10)
式中,α為載荷損耗系數(shù)。
因此,數(shù)控銑床系統(tǒng)在穩(wěn)定切削階段的輸入功率Pi可由切削參數(shù)簡單地表達(dá)為
Pi=P0+Pmec+Pcutting+Ploss=P0+a1n+
(11)
1.2優(yōu)化模型
基于能耗的切削參數(shù)優(yōu)化是實(shí)現(xiàn)能量利用率最大化、加工能耗最小化的重要技術(shù)手段。單位體積能耗ESEC是指去除單位體積材料時(shí)數(shù)控機(jī)床系統(tǒng)所消耗的能量。在銑削加工階段,可用數(shù)控銑床系統(tǒng)的電能消耗Ei與材料去除體積VMRV的比值表示。ESEC表征了輸入電能Ei轉(zhuǎn)移到工件中的能量效率,它是考量數(shù)控銑床系統(tǒng)加工過程能量效率的重要指標(biāo),其本身又是各切削參數(shù)的函數(shù),因此十分適合用于作為切削參數(shù)優(yōu)化的目標(biāo)函數(shù)。ESEC越小,表示完成相同的切削量數(shù)控銑床系統(tǒng)在切削過程中耗能越少,即
(12)
(13)
(14)
式中,P2為穩(wěn)定切削階段輸入功率;L為工步加工長度;Tm為銑削加工時(shí)間;tc為去除材料時(shí)間;tct為磨損換刀時(shí)間;T為刀具壽命[14];yv、p、q、k、μ、m為相應(yīng)的刀具壽命指數(shù),Cv為比例常數(shù),它們均與刀具和材料相關(guān),由經(jīng)驗(yàn)獲得。
優(yōu)化的目標(biāo)是在約束條件下選擇合適的切削參數(shù),獲得最優(yōu)的ESEC。實(shí)際切削加工過程中,切削參數(shù)的選取不是簡單的數(shù)學(xué)問題,還受到銑床功率、刀具強(qiáng)度、加工表面質(zhì)量等諸多因素的制約。在優(yōu)化過程中,這些制約轉(zhuǎn)變成對(duì)優(yōu)化結(jié)果起限制作用的約束條件。
(1)數(shù)控銑床系統(tǒng)允許的轉(zhuǎn)速:
nmin≤n≤nmax
(15)
其中,nmax、nmin分別為數(shù)控銑床系統(tǒng)允許的最大和最小轉(zhuǎn)速。主軸轉(zhuǎn)速n與切削速度vc之間存在如下關(guān)系:
(16)
式中,D為銑刀直徑。
(2)數(shù)控銑床系統(tǒng)允許的進(jìn)給量范圍:
(17)
式中,z為銑刀齒數(shù);vfmax、vfmin分別為機(jī)床允許的最大和最小進(jìn)給速率。
(3)數(shù)控銑床系統(tǒng)允許的切削寬度范圍:
0≤ae≤0.7D
(18)
(4)數(shù)控銑床系統(tǒng)允許的切削深度范圍:
0≤ap≤min(0.5D,7mm)
(19)
(5)數(shù)控銑床系統(tǒng)允許的最大扭矩約束:
(20)
式中,Mmax為機(jī)床主軸最大的輸出扭矩。
(6)數(shù)控銑床系統(tǒng)允許的最大切削功率:
(21)
式中,η為主傳動(dòng)系統(tǒng)效率;Pmax為主電機(jī)額定功率。
(7)粗銑加工的表面質(zhì)量要求如下[10]:
(22)
式中,Ra為表面粗糙度;rε為刀尖圓角半徑;Ramax為加工表面粗糙度的最大值,對(duì)于粗銑加工,Ramax=6.4μm。
綜合上述目標(biāo)函數(shù)、約束條件與參數(shù)表,可知優(yōu)化模型如下:

(23)
生產(chǎn)效率是一個(gè)制造企業(yè)最為重視的目標(biāo),也是優(yōu)化過程必須兼顧的,它直接影響了企業(yè)設(shè)備的利用率和產(chǎn)品生產(chǎn)的周期,更加間接地影響了企業(yè)的資金運(yùn)轉(zhuǎn)周期和經(jīng)營管理。生產(chǎn)效率可由材料去除率vMRR來度量。材料去除率vMRR是指單位時(shí)間內(nèi)去除的金屬材料的體積,在銑削加工階段,可用數(shù)控銑床系統(tǒng)去除材料體積VMRV與切削加工時(shí)間Tm的比值來表示。vMRR越大,表示相同時(shí)間內(nèi)數(shù)控銑床系統(tǒng)去除的金屬材料體積越大,即有
(24)
2 優(yōu)化算法
2.1引力搜索算法
引力搜索算法是Rashedi等[17]在2009年提出的一種基于萬有引力定律的啟發(fā)式算法:“宇宙中的每個(gè)粒子由于彼此之間的萬有引力作用而相互吸引,這個(gè)力與它們質(zhì)量的乘積成正比,與它們的距離的平方成反比。”
對(duì)于一個(gè)n維的搜索空間,假設(shè)有N個(gè)質(zhì)點(diǎn),則定義第i個(gè)質(zhì)點(diǎn)的位置為
(25)

由于多維搜索空間每個(gè)維度上的尺寸差異可能較大,導(dǎo)致質(zhì)點(diǎn)移動(dòng)過程中某些維度上的移動(dòng)速度過快或過慢,采用標(biāo)準(zhǔn)化公式來統(tǒng)一搜索空間尺寸:
(26)

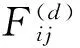
(27)
(28)
式中,Mpi(t)、Maj(t)分別為被作用質(zhì)點(diǎn)i和作用質(zhì)點(diǎn)j的慣性質(zhì)量;Rij(t)為兩質(zhì)點(diǎn)之間的歐氏距離;ε為一個(gè)很小的常量;G(t)為迭代過程的t時(shí)刻對(duì)應(yīng)的引力常數(shù);G0為迭代開始時(shí)刻的引力常數(shù);t為當(dāng)前迭代代數(shù);T為最大迭代次數(shù)。
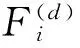
(29)
式中,rj為[0,1]區(qū)間上的隨機(jī)數(shù);Kbest(t)為引力作用數(shù)。
在搜索過程的前期,為了充分勘探整個(gè)搜索空間,任意質(zhì)點(diǎn)之間的相互吸引力都會(huì)影響搜索路徑。隨著迭代的進(jìn)行,全局勘探逐漸淡出,搜索過程更加側(cè)重于局部開發(fā)以獲得最優(yōu)解,僅有慣性質(zhì)量較大的Kbest(t)個(gè)質(zhì)點(diǎn)對(duì)其他質(zhì)點(diǎn)產(chǎn)生吸引。引力作用數(shù)Kbest(t)伴隨迭代次數(shù)的增加線性減小:
(30)

(31)
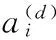
據(jù)此可知,GSA算法每次迭代的質(zhì)點(diǎn)位置更新方式如下式所示:
(32)
在GSA算法中,每個(gè)質(zhì)點(diǎn)的位置坐標(biāo)xi代表了搜索空間的一組可行解。而質(zhì)點(diǎn)的慣性質(zhì)量Mi是按照其適應(yīng)值的大小來計(jì)算的。質(zhì)點(diǎn)慣性質(zhì)量越大,就意味著它越接近最優(yōu)值,對(duì)其他質(zhì)點(diǎn)的吸引力越大,自身的移動(dòng)速度越慢。質(zhì)點(diǎn)的慣性質(zhì)量按下式更新:
(33)
(34)
式中,fi(t)為質(zhì)點(diǎn)i在t時(shí)刻的適應(yīng)值大小;fworst(t)、fbest(t) 分別為適應(yīng)度的最劣值和最優(yōu)值。
2.2優(yōu)化流程

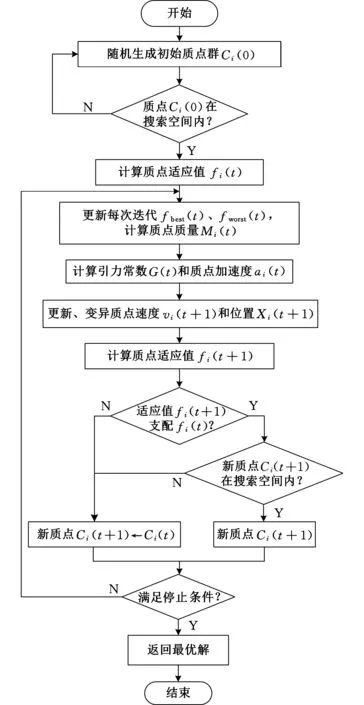
圖2 GSA流程圖
3 實(shí)驗(yàn)與優(yōu)化
3.1功率建模實(shí)驗(yàn)
本實(shí)驗(yàn)以沈陽機(jī)床廠TC500R鉆銑加工中心(FANUC OI MD數(shù)控系統(tǒng))為平臺(tái),在完成平面立銑粗加工的過程中采集功率數(shù)據(jù),通過非線性回歸分析計(jì)算上述模型參數(shù)。實(shí)驗(yàn)中采用直徑為16 mm的3齒超硬直柄立銑刀,在外形尺寸為100 mm×100 mm×40 mm的6061鋁合金方形坯料表面上銑削平面。實(shí)驗(yàn)過程中由布置在數(shù)控銑床系統(tǒng)電氣柜母線上的維博WB9128-1型功率傳感器完成銑削過程中數(shù)控銑床系統(tǒng)的輸入功率的測(cè)量。功率采集方案及實(shí)驗(yàn)裝置如圖3、圖4所示。
為了不失偏頗地考察各個(gè)切削參數(shù)對(duì)輸入功率Pi的影響,本文將各銑削參數(shù)分別分為4個(gè)不同水平,如表1所示,組合以構(gòu)成實(shí)驗(yàn)方案,如表2所示。其中P1表示數(shù)控銑床系統(tǒng)在空切階段的輸入功率。

圖3 功率采集方案

圖4 切削實(shí)驗(yàn)裝置
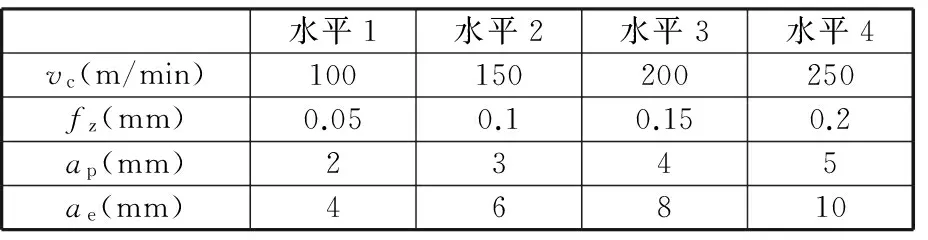
水平1水平2水平3水平4vc(m/min)100150200250fz(mm)0.050.10.150.2ap(mm)2345ae(mm)46810
3.2功率模型分析
根據(jù)上述實(shí)驗(yàn)數(shù)據(jù),應(yīng)用統(tǒng)計(jì)分析軟件OriginPro 8進(jìn)行非線性回歸分析,可得上述模型對(duì)應(yīng)該數(shù)控銑床系統(tǒng)的輸入功率Pi關(guān)于切削參數(shù)的函數(shù):
Pi=448+1.01×10-1n+2.08×10-6n2+
(35)
式中數(shù)控銑削過程固定能耗、機(jī)械損耗、負(fù)載相關(guān)功率各自的比例清晰明確。經(jīng)分析計(jì)算,該模型對(duì)實(shí)驗(yàn)數(shù)據(jù)的擬合誤差最大僅為4.32%,平均精度達(dá)到98.73%。

表2 銑削實(shí)驗(yàn)表
將實(shí)驗(yàn)數(shù)據(jù)應(yīng)用于Li等[6]提出的模型,可以得出數(shù)控銑床輸入功率Pi關(guān)于切削參數(shù)的函數(shù)如下:
Pi=531+9.13×10-2n+8.33×10-1vMRR(W)
(36)
由式(36)計(jì)算分析可知,Li等[6]提出的模型對(duì)本實(shí)驗(yàn)數(shù)據(jù)的平均擬合精度為97.74%,最小誤差為0.14%,最大誤差達(dá)到7.46%,無論最大擬合誤差還是平均擬合精度均劣于式(35)得到的結(jié)果。
式(35)和式(36)對(duì)應(yīng)模型的統(tǒng)計(jì)分析如表3和表4所示,顯然前者擁有更小的均方差和更高的擬合優(yōu)度。對(duì)比模型擬合精度和統(tǒng)計(jì)方差可知,式(35)對(duì)應(yīng)模型由于采用了更加精確的空載損耗模型,包括考慮主軸黏性摩擦損耗和進(jìn)給損耗,以及更加精確的切削功率模型,在理論知識(shí)的指導(dǎo)下合理增加了模型的多項(xiàng)式項(xiàng)數(shù),使得模型在統(tǒng)計(jì)上顯示出更高的精度。可見式(35)對(duì)應(yīng)模型對(duì)數(shù)控銑削過程輸入功率預(yù)測(cè)不僅理論基礎(chǔ)更加堅(jiān)實(shí),而且擬合顯著性水平更高,能耗構(gòu)成成分更加清晰,對(duì)數(shù)控銑床系統(tǒng)節(jié)能優(yōu)化具有重大指導(dǎo)意義。
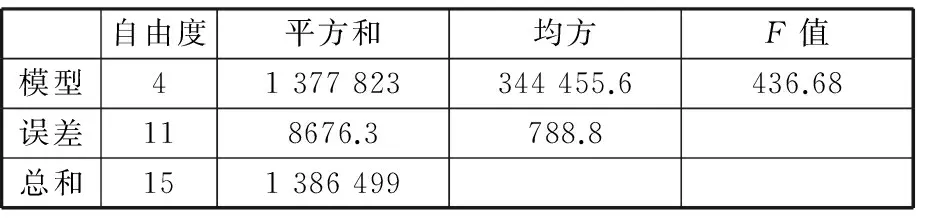
表3 式(35)模型方差分析

表4 式(36)模型方差分析
3.3優(yōu)化與分析
數(shù)控銑床系統(tǒng)和銑刀的具體參數(shù)如表5和表6所示。

表5 機(jī)床與工藝參數(shù)表

表6 刀具參數(shù)表

圖5 n對(duì)ESEC和vMRR的影響趨勢(shì)
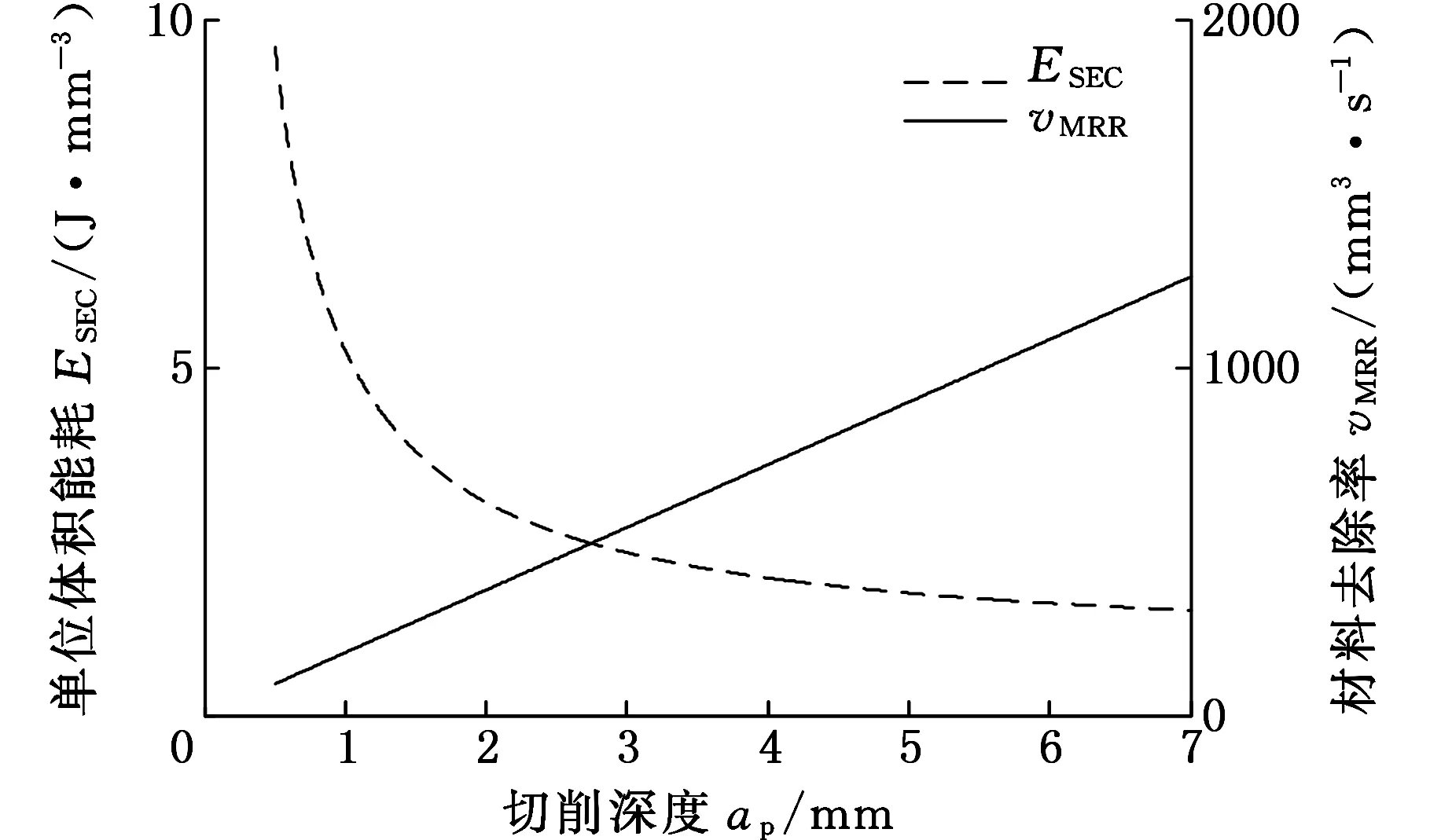
圖6 ap對(duì)ESEC和vMRR的影響趨勢(shì)
圖5、圖6所示分別是在經(jīng)驗(yàn)切削參數(shù)設(shè)置下,主軸轉(zhuǎn)速n和切削深度ap對(duì)單位體積能耗ESEC和材料去除率vMRR的影響趨勢(shì)曲線。從圖中可以看出,n與ap對(duì)ESEC和vMRR的影響趨勢(shì)大致相同。隨著n或ap的增大,ESEC呈現(xiàn)減小的趨勢(shì),而vMRR呈近似線性增大。在圖5中,隨著n的增大,數(shù)控銑床輸入功率Pi增大,切削時(shí)間tc急劇縮短,綜合體現(xiàn)為銑床能耗的快速降低,而單一工步的切削體積仍保持不變,因此ESEC相應(yīng)快速降低。在圖6中,同樣地,銑床輸入功率Pi隨ap的增大而增大,切削時(shí)間tc不受影響,單一工步消耗的電能增加,切除的體積同樣增加,最終表現(xiàn)為ESEC降低,但減小速率相對(duì)較小。兩圖中vMRR均呈近似線性增長,說明該切削條件下刀具磨損量不大,換刀時(shí)間相對(duì)切削時(shí)間tc的比例較小,vMRR接近于瞬時(shí)材料去除率,與n、fz、ap、ae均成線性關(guān)系。進(jìn)給量fz和切削寬度ae對(duì)單位體積能耗ESEC和材料去除率vMRR的影響趨勢(shì)與之類似。
為了保證優(yōu)化模型的可用性,進(jìn)一步確保優(yōu)化參數(shù)的準(zhǔn)確性,將轉(zhuǎn)速n和進(jìn)給量fz作如下限制:n∈[1989, 4973]r/min,fz∈[0.05, 0.2]mm。GSA優(yōu)化算法采用C++程序?qū)崿F(xiàn),在Windows 8.1操作系統(tǒng)、Core i5 CPU、4G內(nèi)存家用筆記本電腦上運(yùn)行。算法參數(shù)設(shè)置如表7所示。

表7 GSA參數(shù)設(shè)置
如表8所示,經(jīng)GSA計(jì)算,得到以穩(wěn)定銑削過程最小單位體積能耗ESEC為目標(biāo)的優(yōu)化的切削參數(shù)設(shè)置:主軸轉(zhuǎn)速n為4973 r/min,每齒進(jìn)給量fz為0.2 mm,銑削深度ap為7 mm,切削寬度ae為11.2 mm。對(duì)比經(jīng)驗(yàn)的切削參數(shù)設(shè)置,優(yōu)化后的參數(shù)使數(shù)控銑床系統(tǒng)穩(wěn)定切削階段的能量效率ηP從39.06%提高至63.64%,單位體積能耗ESEC從1.9780 J/mm3降至0.9895 J/mm3,降幅達(dá)49.97%。在節(jié)能的同時(shí)兼顧了生產(chǎn)效率,材料去除率vMRR得到大幅提升。以數(shù)控銑床系統(tǒng)每天實(shí)際切削的時(shí)間4 h、每年投入使用300天計(jì),優(yōu)化后一臺(tái)數(shù)控銑床系統(tǒng)每年完成相同的切削工作量,銑削過程節(jié)能將達(dá)到854 kW·h,累計(jì)節(jié)省工時(shí)達(dá)222 h。如將之進(jìn)一步推廣應(yīng)用于行業(yè)內(nèi)眾多數(shù)控機(jī)床系統(tǒng),其節(jié)能效果無疑是巨大的。
從表8可以看出,依經(jīng)驗(yàn)選取的切削參數(shù)極大地浪費(fèi)了數(shù)控機(jī)床系統(tǒng)的加工能力。優(yōu)化結(jié)果脫離了經(jīng)驗(yàn)參數(shù)的束縛,以數(shù)控銑床系統(tǒng)的加工能力與加工表面質(zhì)量要求為實(shí)際量化約束,最大限度地利用了數(shù)控銑床系統(tǒng)性能潛力,同時(shí)大幅提高了銑床系統(tǒng)的能量效率。

表8 切削參數(shù)優(yōu)化前后對(duì)比
4 結(jié)論
(1)在分析數(shù)控銑床系統(tǒng)輸入功率去向構(gòu)成的基礎(chǔ)上,通過逐項(xiàng)分離建立了數(shù)控銑床系統(tǒng)輸入功率模型。從銑削實(shí)驗(yàn)功率數(shù)據(jù)中擬合出輸入功率關(guān)于切削參數(shù)的函數(shù),并對(duì)比Li等[6]模型擬合得出的功率函數(shù),結(jié)果顯示本文建立的模型具有更高的擬合精度,而且理論基礎(chǔ)更強(qiáng),能耗去向明確。
(2)在輸入功率模型的基礎(chǔ)上,以穩(wěn)定切削過程最小單位體積能耗為目標(biāo),以數(shù)控銑床系統(tǒng)加工能力和加工表面質(zhì)量為約束,應(yīng)用改進(jìn)的引力搜索算法求解,得到理論最優(yōu)的切削參數(shù)組合。對(duì)比經(jīng)驗(yàn)的切削參數(shù)設(shè)置,優(yōu)化后的切削參數(shù)顯著提高了機(jī)床的能量效率,同時(shí)單位體積能耗大幅降低。
(3)在數(shù)控銑床系統(tǒng)輸入功率建模方面,變頻器損耗、電機(jī)電磁損耗等由于理論復(fù)雜,在模型中尚未清晰體現(xiàn)。在切削參數(shù)優(yōu)化方面,機(jī)床啟動(dòng)階段、待機(jī)階段、空切階段能耗尚未納入考慮;針對(duì)具體加工環(huán)境的實(shí)際約束,如工件強(qiáng)度、排屑控制等尚未在優(yōu)化模型中實(shí)現(xiàn),上述缺點(diǎn)都將是下一步研究工作的重點(diǎn)。
[1]AbeleE,AnderlR,BirkhoferH.Environmentally-friendlyProductDevelopment:MethodsandTools[M].London:SpringerverlagLondonLimited, 2005.
[2]SteinerR,FrischknechtR.MetalsProcessingandCompressedAirSupply.No23[R].Switzerland:EcoinventReport, 2007.
[3]JiangZ,ZhangH,YanW,etal.AnEvaluationModelofMachiningProcessforGreenManufacturing[J].AdvancedScienceLetters, 2011, 4(4/5):1724-1728.
[4]AggarwalA,SinghH,KumarP,etal.OptimizingPowerConsumptionforCNCTurnedPartsUsingResponseSurfaceMethodologyandTaguchi’sTechnique—aComparativeAnalysis[J].JournalofMaterialsProcessingTechnology, 2008, 200(1):373-384.
[5]GutowskiT,DahmusJ,ThiriezA.ElectricalEnergyRequirementsforManufacturingProcesses[C]//13thCIRPInternationalConferenceonLifeCycleEngineering.Leuven:CIRP,2006:560-564.
[6]LiL,YanJ,XingZ.EnergyRequirementsEvaluationofMillingMachinesBasedonThermalEquilibriumandEmpiricalModelling[J].JournalofCleanerProduction, 2013, 52:113-121.
[7]劉飛, 劉霜. 機(jī)床服役過程機(jī)電主傳動(dòng)系統(tǒng)的多時(shí)段能量模型[J]. 機(jī)械工程學(xué)報(bào), 2012, 48(21):132-140.
LiuFei,LiuShuang.Multi-periodEnergyModelofElectro-mechanicalMainDrivingSystemduringtheServiceProcessofMachineTools[J].ChineseJournalofMachineEngineering, 2012, 48(21):132-140.
[8]SonmezAH,BaykasoLuA,DereliT,etal.DynamicOptimizationofMultipassMillingOperationsviaGeometricProgramming[J].InternationalJournalofMachineToolsandManufacture, 1999,39(2):297-320.
[9]WangZG,RahmanM,WongYS,etal.OptimizationofMulti-passMillingUsingParallelGeneticAlgorithmandParallelGeneticSimulatedAnnealing[J].InternationalJournalofMachineToolsandManufacture, 2005,45(15):1726-1734.
[10]TandonV,El-MounayriH,KishawyH.NCEndMillingOptimizationUsingEvolutionaryComputation[J].InternationalJournalofMachineToolsandManufacture, 2002,42(5):595-605.
[11]劉海江, 黃煒. 基于粒子群算法的數(shù)控加工切削參數(shù)優(yōu)化[J]. 同濟(jì)大學(xué)學(xué)報(bào)(自然科學(xué)版), 2008,36(6):803-806.
LiuHaijiang,HuangWei.ComputerNumericalControlMachiningParameterOptimizationBasedonParticleSwarmOptimization[J].JournalofTongjiUniversity(NaturalScience), 2008,36(6):803-806.
[12]JafarianF,TaghipourM,AmirabadiH.ApplicationofArtificialNeuralNetworkandOptimizationAlgorithmsforOptimizingSurfaceRoughness,ToolLifeandCuttingForcesinTurningOperation[J].JournalofMechanicalScienceandTechnology, 2013,27(5):1469-1477.
[13]HeY,LiuB,ZhangX,etal.AModelingMethodofTask-orientedEnergyConsumptionforMachiningManufacturingSystem[J].JournalofCleanerProduction, 2012,23(1):167-174.
[14]許弟建, 施金良. 機(jī)床功率測(cè)試系統(tǒng)設(shè)計(jì)與節(jié)能方法[J]. 組合機(jī)床與自動(dòng)化加工技術(shù), 2010(3):47-51.
XuDijian,ShiJinliang.TheDesignofActivePowerTestSystemandEnergySavingMethodofNCMachineTool[J].ModularMachineToolandAutomaticManufacturingTechnique, 2010(3):47-51.
[15]施金良, 劉飛, 許弟建, 等. 數(shù)控機(jī)床空載運(yùn)行時(shí)節(jié)能決策模型及實(shí)用方法[J]. 中國機(jī)械工程, 2009,20(11):1344-1346.
ShiJinliang,LiuFei,XuDijian,etal.DecisionModelandPracticalMethodofEnergy-savinginNCMachineTool[J].ChinaMechanicalEngineering, 2009,20(11):1344-1346.
[16]施金良, 劉飛, 許弟建, 等. 變頻調(diào)速數(shù)控機(jī)床主傳動(dòng)系統(tǒng)的功率平衡方程[J]. 機(jī)械工程學(xué)報(bào), 2010,46(3):118-124.
ShiJinliang,LiuFei,XuDijian,etal.PowerBalanceEquationabouttheNumericalControlMachineTool’sMainDriverSystemDrivenbyVariableVoltageVariableFrequency[J].JournalofMachineEngineering, 2010,46(3):118-124.
[17]RashediE,NezamabadiPH,SaryazdiS.GSA:AGravitationalSearchAlgorithm[J].InformationSciences, 2009, 179(13):2232-2248.
[18]ShiY,EberhartR.AModifiedParticleSwarmOptimizer[C]//IEEEWorldCongressonComputationalIntelligence.EvolutionaryComputationProceedings.NewJersey:IEEEPress, 1998:69-73.
[19]NobahariH,NikusokhonM,SiarryP.Non-dominatedSortingGravitationalSearchAlgorithm[C]//Proc.ofthe2011InternationalConferenceonSwarmIntelligence.Cergy:ICSI, 2011:1-10.
(編輯王艷麗)
Energy-oriented CNC Milling Process Modelling and Parameter Optimization
Huang Zhengtao1Yang Jie2Zhang Chaoyong1Zhou Zhiheng1Xie Yang1Lin Wenwen1
1.State Key Laboratory of Digital Manufacturing Equipment and Technology,Huazhong University of Science and Technology,Wuhan,430074 2.China University of Geosciences,Wuhan,430074
In order to select the appropriate cutting parameters to reduce energy consumption, a stable CNC milling process was modeled and optimized based on energy consumption function. First of all, the input power model of CNC milling system was built by characterizing its components. Then an energy consumption test platform was set up. The function between the input power of CNC milling system and cutting parameters was established through multiple regression, and its accuracy was confirmed by a comparative analysis. After that the specific energy consumption function during stable CNC milling process was figured out from the input power function. GSA was used to optimize the cutting parameters by a model, which regarded theESECas goal and the performance of milling machine and surface quality as constraints. Compared with empirical data, it is shown that the optimized cutting parameters will improve the energy efficiency of milling machine significantly and drastically.
CNC milling machine; energy saving; power model; optimization of cutting parameters; gravitational search algorithm(GSA)
2015-11-24
國家自然科學(xué)基金資助項(xiàng)目(51575211, 51275190);國家自然科學(xué)基金國際(地區(qū))合作與交流項(xiàng)目(51561125002);中央高校基本科研業(yè)務(wù)費(fèi)專項(xiàng)資金資助項(xiàng)目(2014TS038)
TH18
10.3969/j.issn.1004-132X.2016.18.019
黃拯滔,男,1990年生。華中科技大學(xué)機(jī)械科學(xué)與工程學(xué)院碩士研究生。研究方向?yàn)閿?shù)控機(jī)床高效低碳運(yùn)行、綠色制造、智能優(yōu)化算法等。楊杰,男,1968年生。中國地質(zhì)大學(xué)(武漢)機(jī)械與電子信息學(xué)院教授。張超勇,男,1972年生。華中科技大學(xué)機(jī)械科學(xué)與工程學(xué)院副教授。周志恒,男,1991年生。華中科技大學(xué)機(jī)械科學(xué)與工程學(xué)院碩士研究生。謝陽,男,1987年生。華中科技大學(xué)機(jī)械科學(xué)與工程學(xué)院博士研究生。林文文,男,1989年生。華中科技大學(xué)機(jī)械科學(xué)與工程學(xué)院博士研究生。

