帶柔性時間窗車輛路徑問題的混沌蟻群算法*

趙玉蘋 張惠珍

（上海理工大學　　管理學院，上海，200093）

帶柔性時間窗車輛路徑問題的混沌蟻群算法*

趙玉蘋 張惠珍

（上海理工大學管理學院，上海，200093）

帶柔性時間窗的開放式車輛路徑問題（Opening Vehicle Routing Problemwith Flexible Time Windows，OVRPFTW）對物流配送中的延遲或者提早具有一定程度的容忍.本文首先建立了OVRPFTW的數學模型，然后分別將Sine映射，Chebyshev映射和Logistic映射引入基本蟻群算法，構建了三種混沌蟻群算法，并將其用于求解OVRPFTW.算例測試表明：Sine映射和Chebyshev映射能夠明顯地改進基本蟻群算法的優化性能，基于Sine映射和Chebyshev映射的混沌蟻群算法的求解性能優于基本蟻群算法和基于Logistic映射的混沌蟻群算法.

車輛路徑問題 柔性時間窗 混沌優化 蟻群算法

1　引言

開放式車輛路徑問題（Opening Vehicle Routing Problem）和帶時間窗的車輛路徑問題（Vehicle Routing Problem with Time Windows，VRPTW）是組合優化問題中應用相當廣泛的模型［1］，它們是車輛路徑問題（Vehicle Routing Problem，VRP）的擴展.在物料運輸、郵政快遞以及校車路徑規劃中都可以看到VRPTW的應用，它要求為顧客提供服務的時間必須在此顧客的時間窗內，允許車輛在顧客服務時間窗開始之前到達，并且在等待期間不產生成本，但是不允許車輛在顧客服務時間窗結束之后到達.帶軟時間窗的車輛路徑問題（Vehicle Routing Problem with Soft Time Windows，VRPSTW）假定可以違背顧客服務時間窗，但必須要為車輛的早到或者遲到接受適當的懲罰［2］.對于開放式車輛路徑問題（Opening Vehicle Routing Problem，OVRP）來說，不要求車輛完成配送任務后返回原出發點，若要求返回原出發點，則沿原路線返回［3］.目前，用于求解開放式且有時間要求的物流配送問題的啟發式算法主要包括：模塊啟發式算法［4］，混合粒子禁忌搜索算法［5］，變鄰域搜索算法［6］，蟻群算法［7］，遺傳算法［8-10］等等，這些算法主要用于解決帶硬時間窗或軟時間窗的開放式車輛路徑問題.

帶柔性時間窗的開放式車輛路徑問題（Opening Vehicle Routing Problem with Flexible Time Windows，OVRPFTW）表示客戶對配送時間具有一定程度的容忍，容忍度是根據配送物品的特點以及顧客的時間彈性來確定，允許配送時間窗的違反［11］.國內外關于帶柔性時間窗的車輛路徑問題的研究并不多見，而對于多配送中心、開放式的帶柔性時間窗的車輛路徑問題更是鮮有研究.本文首先建立帶柔性時間窗的多配送中心、開放式的車輛路徑問題的數學模型，然后分別將基于Sine映射，Chebyshev映射和Logistic映射的混沌策略引入基本蟻群算法，構建了三種不同的混沌蟻群算法，并將其用于求解OVRPFTW，最后通過測試算例分析了三種混沌蟻群算法和基本蟻群的求解性能.

2　帶柔性時間窗的多配送中心開放式車輛路徑問題

2.1問題及描述符號定義

帶柔性時間窗的多配送中心開放式車輛路徑問題可以描述為：車輛k從配送中心D出發，一次為多個顧客配送貨物，配送完成之后返回就近的配送中心.其中，每個顧客i只能被一輛車服務且只能被服務一次.假設顧客i的服務時間窗為［li，ui］，考慮到該時間窗對早到或晚到具有一定的容忍度后的時間窗為［l′i，u′i］，車輛k超出這一限定區間到達要受到一定的懲罰，即若車輛k早到，則必須等到最早開始服務時間l′i才能服務；若車輛k晚到，則必須在最晚開始服務時間u′i之前到達.該問題的目標是求解從所有配送中心出發的車輛對所有顧客配送服務的最小運輸總成本，這里的運輸成本包括固定成本和可變成本，固定成本為車輛啟動費用，可變成本只考慮車輛的行駛距離.

為便于問題描述，現將變量及符號定義如下：

G=（V，E）：運輸網絡；V：節點集，包括客戶集C=1，2，…，A｛

｝和配送中心集D= 1，2，…，B｛

｝，任意一個配送中心車輛的集合；o：油耗費用系數；r：調用一輛車的固定啟動費用系數；W：每輛車的最大裝載量；［li，ui］：客戶點i的時間窗；pli：違背客戶i時間窗早到的最大容忍度；pui：違背客戶i時間窗晚到的最大容忍度；：考慮客戶i 最大容忍度的時間窗，其中；tik：車輛k到達客戶點i的時間；tij：每輛車從節點i到節點j的行駛時間；t0：每輛車在客戶點的服務時間；hij：節點i到j之間的距離；dl：車輛在原時間窗之外，最大容忍時間窗之內早到的懲罰系數；du：車輛在原時間窗之外，最大容忍時間窗之內晚到的懲罰系數；P：懲罰函數，

決策變量：

2.2數學模型

上述模型中，式（1）為目標函數，表示車輛運行總成本最小；約束（2）表示每個客戶必須被服務且只能被服務一次；約束（3）和（4）確保客戶僅被訪問一次，且從客戶點離開的車輛僅有一輛；約束（5）保證每輛車不會從一個配送中心不經過客戶直接到達另一個配送中心；約束（6）為車容量約束；約束（7）表示到達客戶點i的車輛數與離開客戶點i的車輛數相同且均為1；約束（8）為時間窗約束；式（9）為計算車輛k到達節點j的時間公式；約束（10）保證車輛行駛的先后順序；約束（11）為消去支路約束，排除不完整線路.

3　混沌蟻群算法

蟻群算法是模擬蟻群覓食行為的一種基于種群的模擬進化算法，其在求解組合優化難題和連續優化問題中取得了較好的結果［12］.近年來，越來越多的學者利用蟻群算法求解物流配送中的車輛調度和路徑優化問題［13］.相比于其他智能優化算法，蟻群算法具有較強的魯棒性，易與其他方法結合的優點.首先，蟻群算法對初始路線的要求不高，即蟻群算法的求解結果不依賴于初始路線的選擇，而且在搜索的過程中不需要進行人工調整.其次蟻群算法的參數數目少，設置簡單.但蟻群算法也具有一定的不足之處，如：容易陷入局部最優，搜索速度比較慢等.

本文針對基本蟻群算法收斂速度慢和易陷入局部最優等缺點，分別將Sine映射，Chebyshev映射和Logistic映射三種混沌映射方法與蟻群算法結合，設計不同的混沌蟻群算法，以便有效抑制算法的早熟現象，跳出局部最優.

3.1混沌擾動策略

混沌是一種普遍的非線性現象，其表面上是混亂的，但實際上卻含有內在規律性，規律性、隨機性和遍歷性是混沌的特點.混沌優化的基本思想是：將優化變量通過混沌映射規則映射到混沌變量空間的取值區間內，利用混沌變量的遍歷性和規律性尋優搜索，最后將獲得的優化解線性轉化到優化空間.

當蟻群算法循環迭代中最優解的值（最小費用）連續重復出現多次時，即可認定算法進入早熟、停滯的狀態.蟻群算法進入早熟、停滯狀態后，可利用混沌擾動策略幫助其跳出局部最優.不同的混沌映射產生的混沌效果不同，本文分別利用Logistic混沌映射、Chebyshev混沌映射和Sine混沌映射（三種混沌的參數、映射表達式和區間表達式如表1所示）調整螞蟻算法中螞蟻的信息素含量，構建了三種不同的混沌蟻群算法.

表1　三種混沌擾動策略

表1中，g表示選出的需要混沌的路徑個數；n表示混沌迭代次數；xn為第n次混沌迭代的數值；τg為第g個要進行混沌的螞蟻信息素含量；τmax表示所選螞蟻路徑上信息素含量的最大值；τmin表示所選螞蟻路徑上信息素含量的最小值.

混沌優化過程為：假設進入混沌迭代時各路徑的信息素含量為τi（0＜i≤m，m為螞蟻數），首先利用映射空間計算表達式將信息素含量轉換到各混沌策略的映射空間上；然后用映射表達式對得到的x1進行混沌擾動，得到混沌序列x=x1，x2，…，xn（

），最后將混沌序列通過逆映射表達式映射到解空間.若混沌迭代過程中更新了全局最優解或達到最大混沌迭代次數仍未更新最優解，則停止混沌擾動.

3.2混沌蟻群算法的設計

3.2.1轉移規則

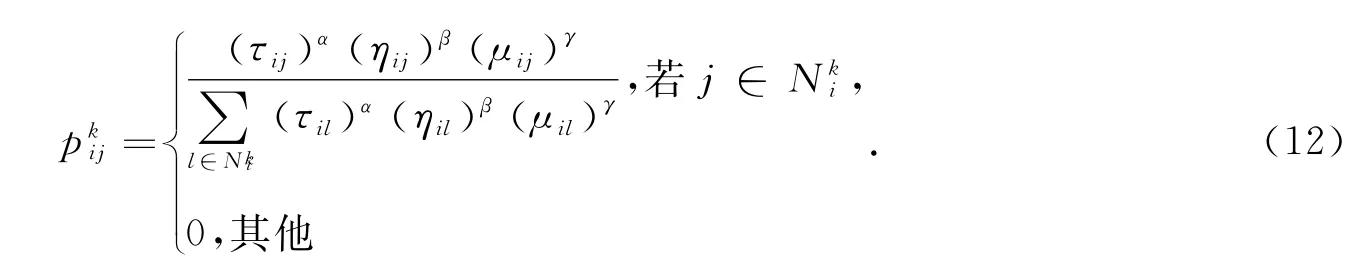
式（12）中，Nki代表螞蟻k可以訪問的客戶點集；τij為邊（i，j）的軌跡強度；ηij為邊（i，j）的能見度，一般表示為路徑長度的倒數；μij為邊（i，j）的節省量，即uij=hib+hbj-hij（b ∈D），節省量的值越大表示螞蟻越應當在訪問完節點i之后訪問節點j.α，β和γ分別表示τij，ηij和μij的相對重要性.

螞蟻構造路徑時，遵循以下的偽隨機規則：q為0到1之間的隨機數，當q＞q0（q0=0.05）時，根據式（12）計算出的轉移概率并按照輪盤賭的方法確定下一個訪問客戶；否則，取轉移概率最大的點為下一個要訪問的客戶點n，即

3.2.2信息素更新

當所有螞蟻完成一次循環迭代后，各邊上的信息素強度由式（14）-（16）進行更新：

3.3算法

求解帶柔性時間窗、多配送中心、開放式車輛路徑問題的混沌蟻群算法的步驟如下：

步驟1 初始化各參數，輸入所有客戶及配送中心的數據，最大迭代次數Nc_max=200；

步驟2 將m只螞蟻隨機均勻地放到B個配送中心，初始化螞蟻k已走的客戶點集tabuk，以及候選點集Nki（包括配送中心）；設置完成任務的螞蟻數量l=0；

步驟3 對螞蟻k，當車輛剩余載重量能滿足至少一個客戶時，按轉移規則確定下一個訪問節點j，并更新tabuk，Nki以及車輛的剩余載重量；

步驟4 如果Nki≠?，并且至少有一個候選點的需求量小于車輛的剩余載重，則轉步驟3；否則轉步驟5；

步驟5 若Nki≠?，并且車輛剩余載重不能滿足所有候選點的需要量，則增加一輛車，令其載重量為W，并轉步驟3；否則，轉步驟6；

步驟6 若Nki=?，且當前螞蟻的最后一個訪問點不是配送中心，則令其返回到離其最近的配送中心，l++.若l≤m，轉步驟3；否則，轉步驟7；

步驟7 所有螞蟻遍歷一次后，按照公式（14）-（16）對所有路徑的信息素進行更新；Nc ++；

步驟8 由各螞蟻的tabuk得到路徑集L=L1，L2，…，Lm｛

｝，根據約束條件計算每個可行解的罰函數以及目標函數值，記錄本次迭代的最優解，同時更新全局最優解（全局最優解為迭代至今求得的最優解）；

步驟9 若同一全局最優解連續出現Nbest_max 次，則轉步驟10，否則轉步驟11；

步驟10 利用混沌映射改變路徑上信息素含量，求出可行解的目標函數值并與當前全局最優解比較，若混沌過程中得到了優于當前最優的解，則更新全局最優解，并跳出混沌迭代；若在混沌迭代過程中未找到優于當前最優的解，直接跳出混沌過程.

步驟11 若Nc=Nc_max ，則算法終止，并輸出全局最優解L*；否則，Nc++，轉步驟2.

4　算例及分析

本文利用文獻［10］中的算例來測試算法的求解性能，其中客戶點、配送中心的位置坐標以及需求量等數據如表2所示.設1-24為客戶編號，25-27為配送中心編號，它們分布在不同的地方.所有車輛的裝載容量為4t，車輛在顧客點的服務時間t0為定值20.

算法運行環境為Windows7平臺，32位操作系統，Intel處理系統，3.40GHz，4 GB內存；仿真軟件為MATLAB2010a.

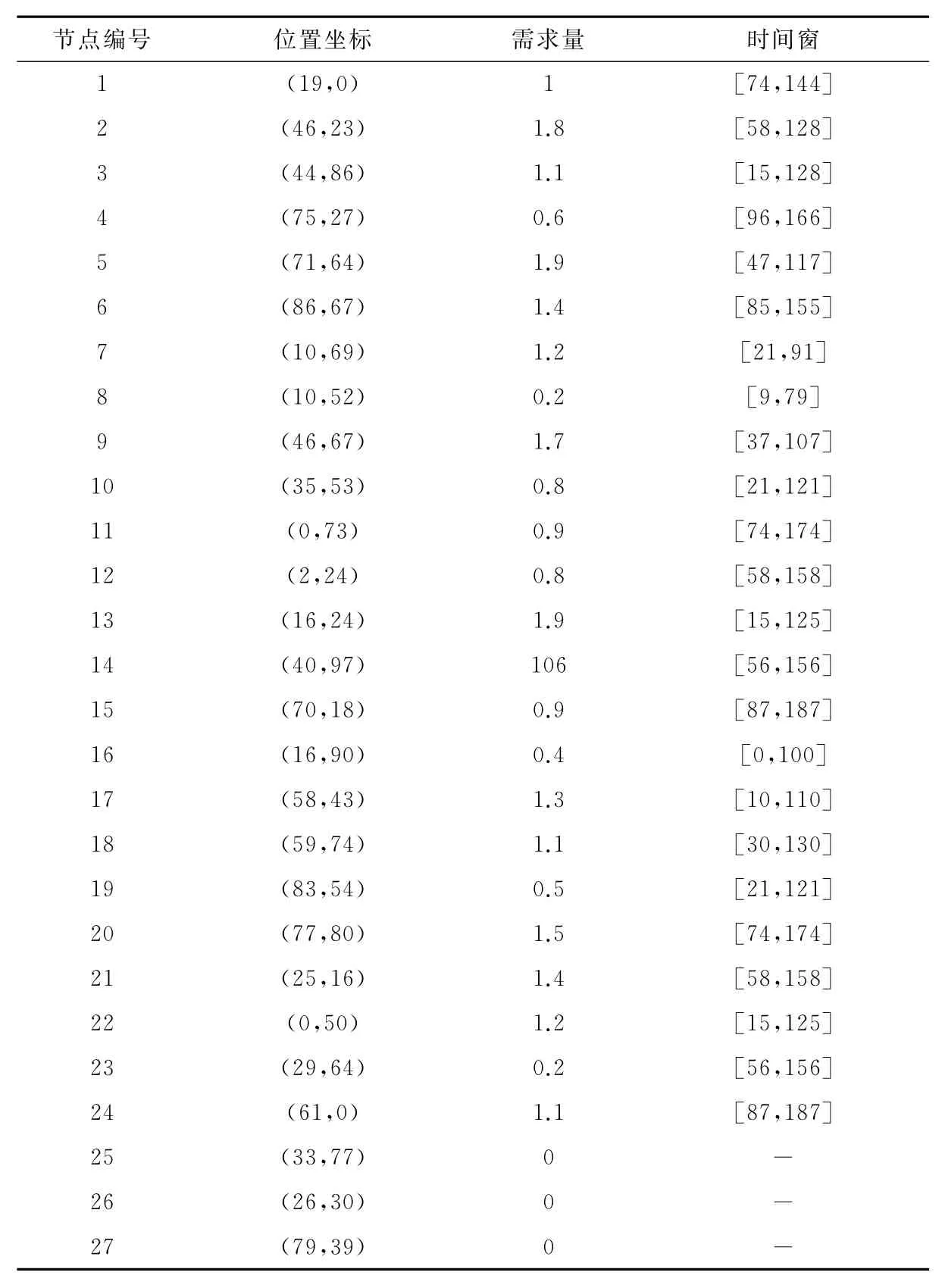
表2　算例數據

為了確保算法之間的可比性，使它們在相同的起點上進行比較，計算過程中對三種混沌蟻群算法和基本蟻群算法共有的參數設定了相同的值：螞蟻數m=60，軌跡的相對重要性α=1，能見度的相對重要性β=1，節省量的相對重要性γ=2，初始信息素總量Q=10，時間窗容忍度ρli=ρui=0.2，算法迭代次數Nc_max=200.對三種混沌迭代中的共有參數設定如下：達到混沌標準的最優解重復次數Nbest_max=30，最大混沌迭代次數Tc=10.三種混沌蟻群算法和基本蟻群算法各運行20次，求解結果如表3所示.

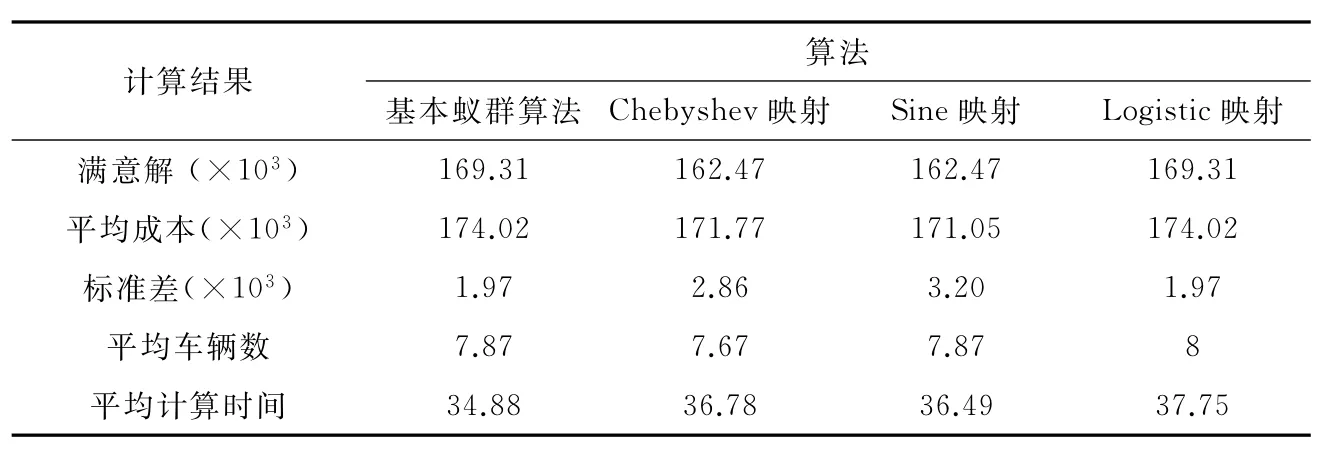
表3　基本蟻群算法與混沌蟻群算法計算結果

由表3不難看出，雖然基本蟻群算法的計算效率以及計算結果的穩健性要高于幾種混沌蟻群算法，但基于Sine映射的混沌蟻群算法和基于Chebyshev映射的混沌蟻群算法的優化結果明顯優于基于Logistic映射的混沌蟻群算法和基本蟻群算法，且Sine映射的混沌蟻群算法的計算結果更優，Chebyshev映射的混沌蟻群算法穩定性更好.與基本蟻群算法相比，帶Logistic映射的混沌蟻群算法并沒有改善問題的最優解，且計算時間更長.

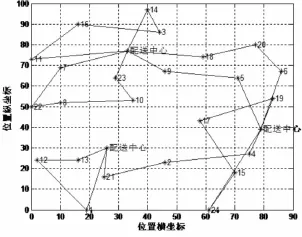
圖1　滿意解圖示

基于Chebyshev映射和Sine映射的混沌蟻群算法求得相同的滿意解（如圖1所示），配送總成本為162472.50，車輛數為7.每輛車的配送路線如下，車輛1：25-16-11-8-22-7-25；車輛2：25-14-3-18-23-25；車輛3：25-9-5 -27；車輛4：27-20-6-19-27；車輛5：27-4 -15-24-17-27；車輛6：27-2-10-21-26；車輛7：26-13-12-1-26.

5　結論

本文首先建立了帶柔性時間窗的開放式車輛路徑問題（OVRPFTW）的數學模型，然后將Sine映射，Chebyshev映射以及Logistic混沌映射分別與基本蟻群算法融合，提出了三種求解OVRPFTW的混沌蟻群算法.測試算例結果表明：基于Sine映射的混沌擾動對蟻群算法在解決帶柔性時間窗的開放式車輛路徑問題中產生了很明顯的優化作用，混沌優化后的最優解平均值171046遠遠優于基本蟻群算法得到的結果174019；利用Chebyshev映射的混沌擾動策略也能夠改進最優解的質量，且穩定性要高于基于Sine映射的混沌蟻群算法；利用Logistic映射的混沌擾動策略對解決此類問題的優化效果卻并不明顯.

［1］A D López-Sánchez，A.G.Hernández-Díaz，Vigo D，et al.A multi-start algorithm for a balanced real -world Open Vehicle Routing Problem［J］.European Journal of Operational Research，2014，238（1）：104-113.

［2］Beheshti A K，Hejazi S R.A novel hybrid column generation-metaheuristic approach for the vehicle routing problem with general soft time window［J］.Information Sciences，2015，316：598-615.

［3］楊進，馬良.蜂群優化算法在帶軟時間窗的車輛路徑問題中的應用［J］.預測，2010，29（6）：67-70.

［4］Rahimi-Vahed A，Crainic T G，Gendreau M，et al.Fleet-sizing for multi-depot and periodic vehicle routing problems using a modular heuristic algorithm［J］.Computers&Operations Research，2015，（53）：9-23.

［5］Escobar J W，Linfati R，Toth P，et al.A hybrid granular tabu search algorithm for the multi-depot vehicle routing problem［J］.Journal of Heuristics，2014，20（5）：483-509.

［6］王征，張俊，王旭坪.多車場帶時間窗車輛路徑問題的變鄰域搜索算法［J］.中國管理科學，2011，（2）：99 -109.

［7］Reed M，Yiannakou A，Evering R.An ant colony algorithm for the multi-compartment vehicle routing problem［J］.Applied Soft Computing，2014，15（2）：169-176.

［8］孫賓松，符卓.求解帶軟時間窗的車輛路徑問題的改進遺傳算法［J］.系統工程，2003，21（6）：12-15.

［9］潘震東，唐加福，韓毅.帶貨物權重的車輛路徑問題及遺傳算法［J］.管理科學學報，2007，10（3）：23-29.

［10］鐘石泉，杜綱，賀國光.有時間窗的開放式車輛路徑問題及其遺傳算法［J］.計算機工程與應用，2007，42（34）：201-204.

［11］Duygu Ta?，Ola Jabali，Tom Van Woensel.A Vehicle Routing Problem with Flexible Time Windows［J］. Computers and Operations Research，2014，52：39-54.

［12］Dorigo M，Bonabeau E，Theraulaz G.Ant algorithms and stigmergy［J］.Future Generation Computer Systems，2000，16（8）：851-871.

［13］李婭，王東.基于混沌擾動和鄰域交換的蟻群算法求解車輛路徑問題［J］.計算機應用，2012，02：444 -447.

The Chaos Ant Colony Optimization Algorithm for Solving Vehicle Routing Problem with Flexible Time Windows

Zhao Yuping Zhang Huizhen
（School of Business，University of Shanghai for Science and Technology，Shanghai 200093，China）

Opening Vehicle Routing Problemwith Flexible Time Windows（OVRPFTW）allows vehicles to serve customers ahead of schedule or behind schedule by a given tolerance.In this paper，the mathematical model of the OVRPFTW is formulated firstly，then three chaos Ant Colony Optimization（ACO）algorithms for solving the OVRPFTW are proposed by combining ACO with Sine mapping，Chebyshev mapping and Logistic mapping，respectively.Numerical results show that Sine mapping and Chebyshev mapping can significantly improve the ACO algorithm，and comparing with the basic ACO algorithm and the chaos ACO algorithm based on Logistic mapping，the chaos ACO algorithms based on Sine mapping and Chebyshev mapping have better optimization performance.

Vehicle routing problem Flexible time window Chaos optimization Ant Colony Optimization

國家自然科學基金項目（71401106）；高等學校博士學科點專項科研基金聯合資助課題（20123120120005）；上海市教育委員會科研創新項目（14YZ090）資助

2016年03月19日