季節性多元回歸模型與時間序列分解模型在內陸用箱需求預測中的應用比較
王騰龍
“一帶一路”戰略的部署和實施推動我國產業結構調整和經濟轉型發展,作為連接絲綢之路經濟帶與海上絲綢之路的橋梁,我國中西部經濟走廊的作用和地位越發顯現。一方面,隨著沿海制造業向內陸轉移,腹地貨源得到釋放,從而帶動物流運輸業發展;另一方面,在世界經濟下行以及集裝箱船舶運力嚴重過剩的背景下,船公司為填滿艙位,爭相通過向內陸延伸海運服務來擴大營銷網絡覆蓋面,以期從源頭上掌握集裝箱貨源,從而提升直接客戶的比例。在內陸存放集裝箱無疑有利于保障客戶裝箱發運的時效性,提升用戶體驗滿意度和客戶黏性;但從經營角度而言,船公司必然要面對如何控制內陸用箱這一現實問題。鑒于內陸出貨有明顯的季節性特點,且內陸調箱存在空間和時間上的局限性,為保障內陸延伸業務穩步開展,船公司需要考慮內陸集裝箱存量問題。本文以內陸進出口箱量的歷史數據為例,分別采用季節性多元回歸模型和時間序列分解模型預測內陸用箱需求,結果表明,時間序列分解模型的預測值更貼近實際觀測值;因此,采用時間序列分解模型預測進出口箱量,可得出下一階段用箱缺口的理論值,從而為船公司主動干預內陸用箱提供量化參考依據。
1 問題描述
在內陸多箱與缺箱之間尋求平衡是船公司業務開拓與成本控制之間的博弈。[1]在實際操作過程中,一方面,為滿足客戶用箱需求,保證集裝箱貨物順利出口,空箱供給需要在特定時間內完成,否則就會產生違約損失和信譽損失,導致船公司丟失市場份額;[2]另一方面,如果過早地預備空箱或管理失控,則會造成空箱積壓,而內陸壓箱的解決方案非常有限,一般只能等待出貨用箱,倘若正值市場淡季,往往會產生高昂的空箱堆存費和調運費。由此可見,適度的內陸存箱規模有助于船公司減少空箱閑置和盲目流動。
內陸用箱供給效率在一定程度上影響著內陸存箱規模。[3]內陸用箱供給主要有以下兩種方式:一種是從口岸調運空箱的“空進重出”方式,由于內陸距口岸箱源地路途遙遠,組織空箱調運的手續煩瑣且費用高昂,難以形成對內陸用箱需求的快速反應和成本優勢,故這種方式很難產生規模效應;另一種是進口重箱在內陸拆空還箱后用于出口的“重進重出”方式,這種方式能夠避免產生口岸調空費、返空費等費用,對內陸用箱而言更具操作性,但受市場季節性波動等因素的影響,內陸進出口箱量、箱型普遍存在較大差異,容易形成被動用箱供給局面,即在缺少預控標準和量化方法的情況下,內陸存箱量不合理,從而產生壓箱或缺箱等負面效果。
將內陸用箱量與存箱量掛鉤并強化預控,有助于提高內陸用箱供給效率。根據精益管理理論中的看板拉動原理,在一段時期內,內陸可接受的進口箱量取決于內陸出口箱量;因此,改變被動用箱供給局面的前提是以合理的方法確定內陸用箱量的變化規律,從而確定合理的存箱量,當內陸空箱盤存量與在途進箱量之和偏離合理的存箱量時發出預警,以便船公司及時采取相應措施主動干預,力求將存箱量控制在合理的范圍內。
對內陸進出口箱量的歷史數據進行分析,發現內陸進出口箱量的季節性特征較為明顯,淡季與旺季的用箱需求存在較大差異。這主要是因為地區間貨源結構不同,例如,進口貨物主要是資源類礦產品,而出口貨物主要是農副加工品,容易導致進出口貨量形成季節性波動,造成進出口箱量不平衡。根據內陸出貨量的時間序列對其進行季節性預測,能夠為合理控制內陸存箱規模提供量化依據。
2 季節性多元回歸模型在內陸出貨量預測中的應用
對于季節性的時間序列,通常采用季節性多元回歸模型進行預測。把季節看作分類變量,用于對數據觀察值進行分類。當分類變量有n個水平時,通常需要(nHa1)個虛擬變量,因此,4個季度需要3個虛擬變量。[4]對3個虛擬變量進行編碼,可以得到:Q1=1(第1季度)或Q1=0(其他季度);Q2=1(第2季度)或Q2=0(其他季度);Q3=1(第3季度)或Q3=0(其他季度)。
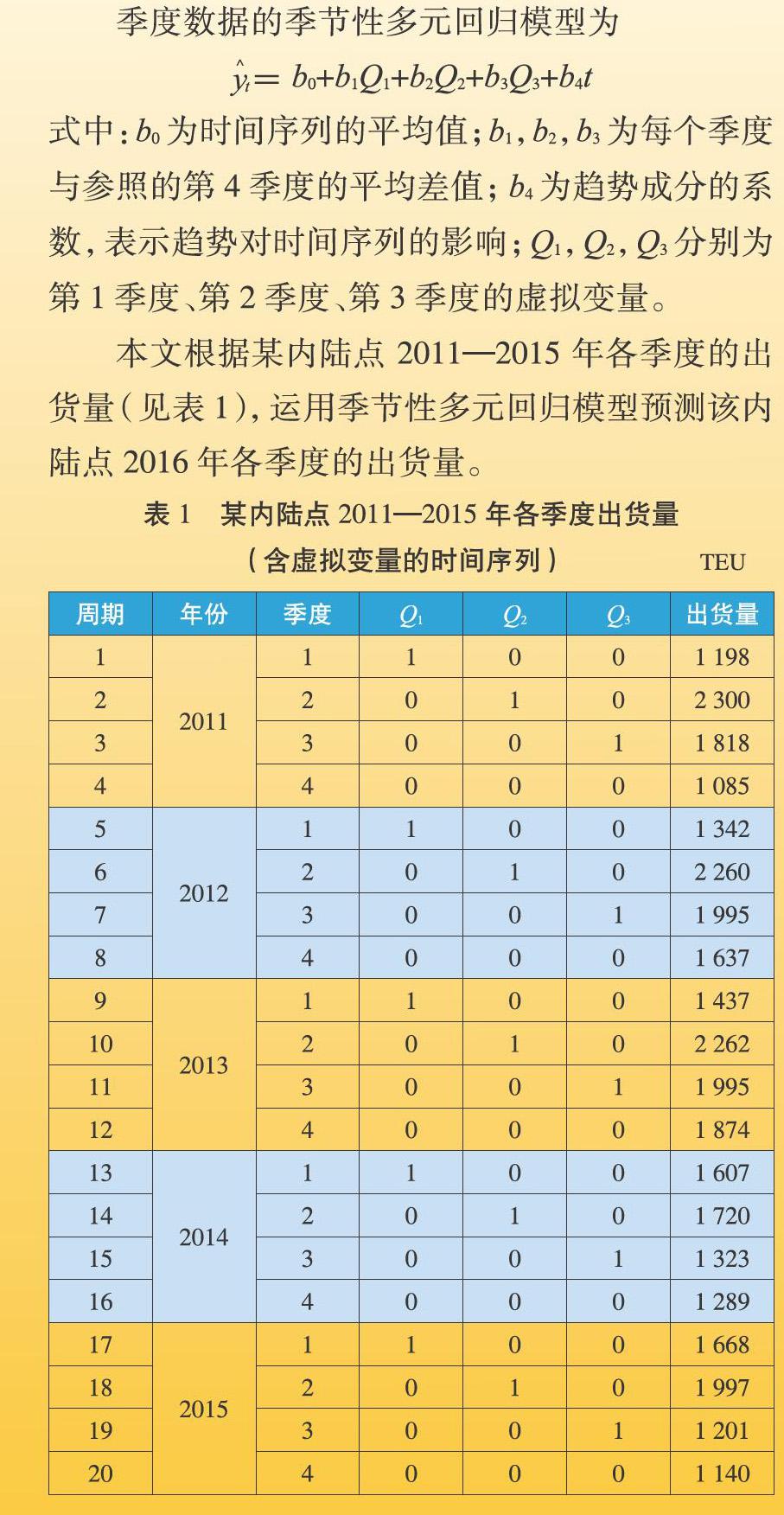
季度數據的季節性多元回歸模型為
=b0+b1Q1+b2Q2+b3Q3+b4t
式中:b0為時間序列的平均值;b1,b2,b3為每個季度與參照的第4季度的平均差值;b4為趨勢成分的系數,表示趨勢對時間序列的影響;Q1,Q2,Q3分別為第1季度、第2季度、第3季度的虛擬變量。
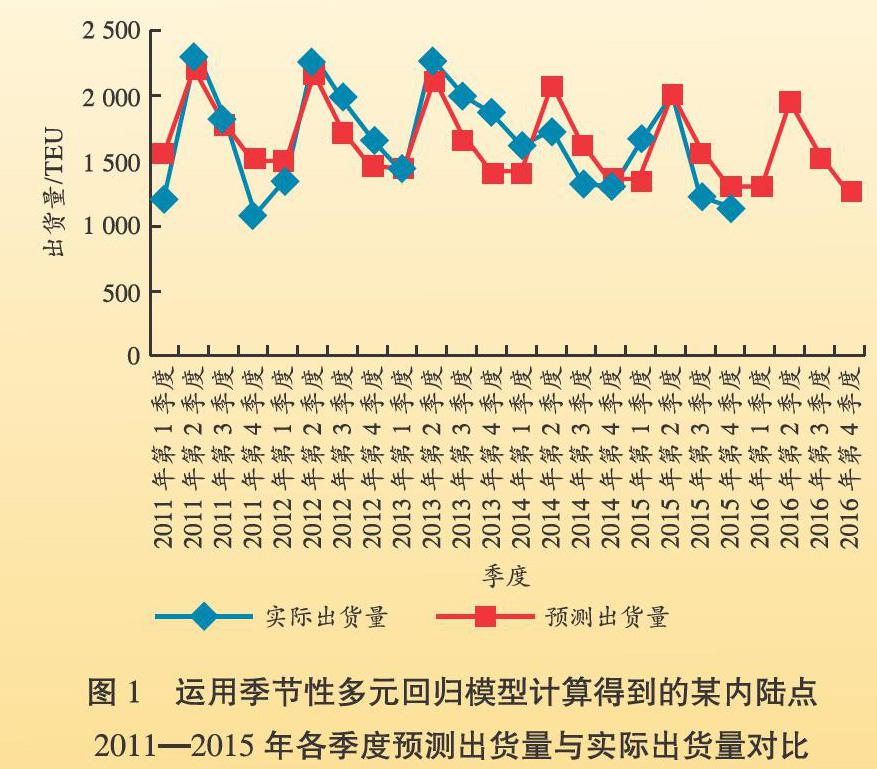
本文根據某內陸點2011―2015年各季度的出貨量(見表1),運用季節性多元回歸模型預測該內陸點2016年各季度的出貨量。
對模型求解,得到回歸方程為
據此預測2016年各季度出貨量,得到第1季度出貨量為,第2季度出貨量為,第3季度出貨量為,第4季度出貨量為。
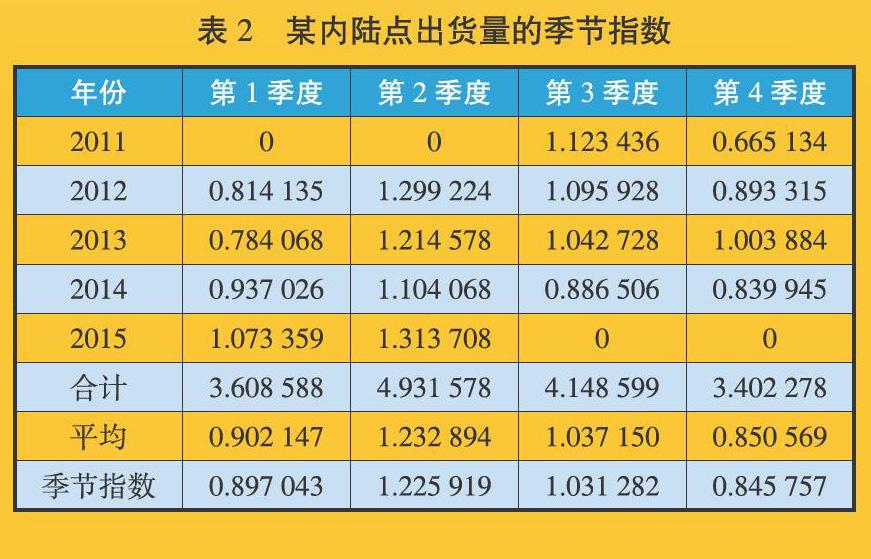
在上述回歸分析中,評估參數R Square和Adjusted R Square的數值偏低,均在0.5左右;評估參數Significance F的數值小于5%,接近于0;評估參數P-value的數值并非都小于5%。以上結果說明該模型的擬合度不理想,導致預測出貨量與實際出貨量之間有較大差距(見圖1)。
3 時間序列分解模型在內陸出貨量預測中的應用
時間序列預測的另一個常用模型是時間序列分解模型,具體方法如下:首先,計算季節指數,以確定時間序列中的季節因素;然后,將季節因素從時間序列中分離出去,以消除季節性;最后,對消除季節因素的時間序列建立預測模型并計算預測值,再回歸相應的季節指數。[5]
季節指數指某一季度的數據與全年平均數據的比值,季節變動的程度根據各季節指數與其平均數(100%)的偏差程度來測定。為求得季節指數,對季節數據進行4項移動平均,并對結果進行中心化處理,計算移動平均的比值,即季節指數。某內陸點出貨量的季節指數如表2所示,分離季節因素后該內陸點出貨量的時間序列如圖2所示。
式中:為分離季節因素后的預測出貨量;b0為趨勢線在縱坐標上的截距;b1為趨勢線的斜率,表示時間周期變動1個單位時觀察值的平均變動數量;t為時間周期。為使b0和b1的數值最優,需要使每一周期時間序列的預測值與觀察值的誤差平方和最小化。令Tt為第t周期時間序列的觀察值,一般模型為
經計算,得到此模型的最優解為b0=1 770.1,b1=Ha10.731,因此,線性趨勢方程為
利用該線性趨勢方程計算得到分離季節因素后的預測出貨量,然后回歸相應的季節指數,得到最終的預測出貨量。
由圖3可見,運用時間序列分解模型得到的預測出貨量與歷史數據非常吻合,說明該模型對季節性貨量的預測效果優于季節性多元回歸模型。建議運用時間序列分解模型預測內陸進出口箱量,并綜合考慮長假、運力調配、工廠檢修等影響因素,據此確定內陸存箱量。
參考文獻:
[1] 安德森D R,斯威尼D J,威廉斯T A,等. 數據、模型與決策:管理科學篇[M]. 侯文華,譯. 北京:機械工業出版社,2012:441-465.
[2]鞠美晨. 基于無水港的集裝箱配備與空箱調運問題研究[D]. 大連:大連海事大學,2013.
[3] 張軍. 平衡為王[J]. 中國遠洋航務,2006(8):40-41.
[4]賈俊平. 統計學[M]. 北京:中國人民大學出版社,2004:323-386.
[5] 宋若辰. 班輪公司集裝箱空箱在途庫存控制研究[D]. 上海:上海交通大學,2012.
(編輯:張敏 收稿日期:2016-04-21)

